一种稳定匹配的任务分配策略研究

高 欣，周绍峰，柳 絮，孙茂圣

(1.扬州大学 信息工程学院, 扬州 2225127)(2.扬州大学 信息化建设与管理处，扬州 2225127)(3.江苏旅游职业学院 信息工程学院, 扬州 225131)

网约车由于其高效性和便利性已逐渐取代传统出租车，成为了人们日常出行的主要交通方式之一.乘客可以通过网约车平台随时发布出行需求，司机可及时获取出行订单，乘客的订单和司机则由平台按照一定规则快速匹配.网约车平台方便快捷的信息交换，大大缓解了传统出租车模式下由于乘客和司机之间的时空偏差造成的信息障碍，成为提高出租车市场效率的有力工具[1-2].近年来，滴滴、Uber、T3出行等国内外网约车平台迅猛扩张.在网约车产业快速发展的背景下，提高网约车效率、优化城市运力、盈利能力已成为研究的不同方向.在城市计算领域，已有大量关于网约车出行的研究，可分为路径规划[3]、订单任务分配[4]、定价策略[5]、补贴策略[6]、共享出行[7-8]、需求预测[9]等.

目前，网约车的订单任务分配策略常见的有两种，分别是抢单模式和派单模式.抢单模式中，网约车平台的主要功能是信息交互，将一名乘客的需求订单信息发送给多名合适的空载司机，司机根据其利益偏好和接单速度进行抢单，在这种模式下，司机选择订单的自由度更高，但也造成了一定的问题，例如第三方软件抢单、低收益订单得不到响应、平台全局效率低等.在派单模式中，网约车平台作为调度系统，根据平台既定规则为司机派发订单，司机仅需执行订单匹配的结果.在该模式下虽然司机失去了选择订单的自由，但匹配率、完成度和全局效率较高，乘客方、司机方以及平台的利益均得到提高.目前，在平台主导权、利益、条件驱使下，多数平台已从抢单模式过渡到派单模式.对于派单模式而言，由网约车平台按既定规则，决定乘客订单的派发司机及派发顺序[10].网约车订单任务分配策略不仅关系着网约车乘客的出行成本、司机的经济效益，同时也影响着网约车平台的利益、用户黏度等.在定位技术和实时交通信息等技术的支持下，网约车平台可以通过高效的订单匹配算法实现限定范围、时间内乘客和司机的较优匹配，提高订单完成度、增加司机经济收益、降低乘客出行成本.正因如此，本文重点在研究网约车派单模式下，订单任务分配策略生成问题.

文中通过派单模式下平台的分配策略，均衡乘客之间、司机之间的利益，同时，又保证分配策略具有较高的订单任务分配率，确保平台收益，保障乘客、司机、平台都能获得较为满意的利益.为了实现上述目标，文中建立了二分匹配模型研究订单任务分配问题，定义了乘客方、司机方的利润函数.并把订单分配分为非共享出行和共享出行两种情况.在非共享出行模型下，进一步将二分匹配模型具体为集合大小不等的稳定匹配问题，提出了基于Gale Shapley (GS)算法的订单任务分配算法，以获得最优稳定匹配及全部稳定匹配.在共享出行模型下，将订单任务分配问题分为订单打包与稳定匹配两部分，订单打包抽象为最大集合打包问题，稳定匹配同非共享出行模型.最后通过在纽约市出租车数据集TCL上执行非共享出行模型及共享出行模型下的算法，和其他主流算法从匹配延迟时间、乘客利益、司机利益等评估指标进行了比较与分析，验证了所提模型的有效性和可行性.

1 非共享出行订单任务模型及分配策略

非共享出行订单任务模型下每个司机至多匹配一个乘客订单，分析该模型下乘客方和司机方的利益，使用基于延迟接受思想的算法求解稳定匹配，并讨论该算法结果的性质.最后，考虑到上述算法存在的局限性，提出了一种求解全部稳定匹配的算法，以供不同需要.

1.1 非共享出行订单任务模型

定义非共享出行订单任务模型为一个三元组NS=，其中：

R为乘客i∈{1,2,...n}发起的订单ri集合；

V为司机j∈{1,2,...m}驾驶的车辆vj集合；

W为乘客发起订单获得的利益w(rj)和司机执行完订单任务后的利益w(vi)的集合.

影响乘客利益的主要因素是等待时间，假设车速恒定的情况下，乘客等待时间与司机接客的路程成正比，乘客更偏好于司机当前位置与订单出发位置间距离更短的订单任务.定义第j个乘客的收益函数w(rj)为：

w(rj)=D(p(vi),s(rj))

(1)

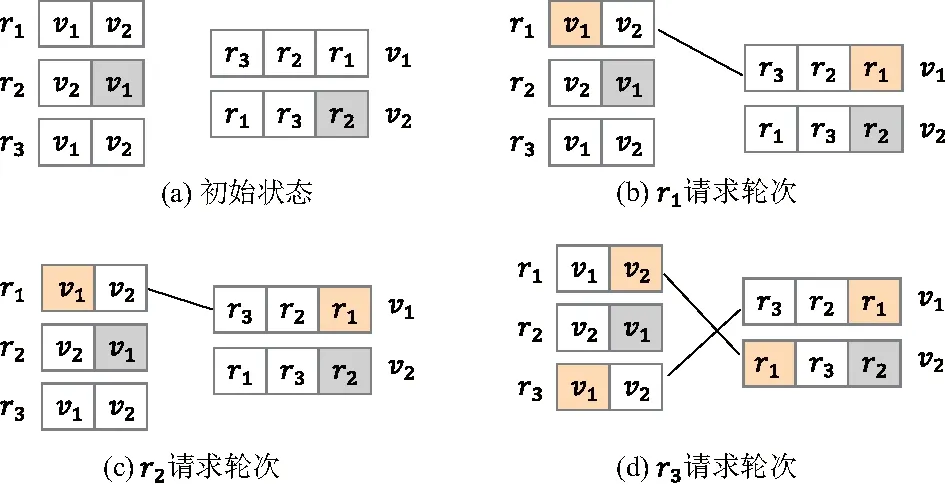
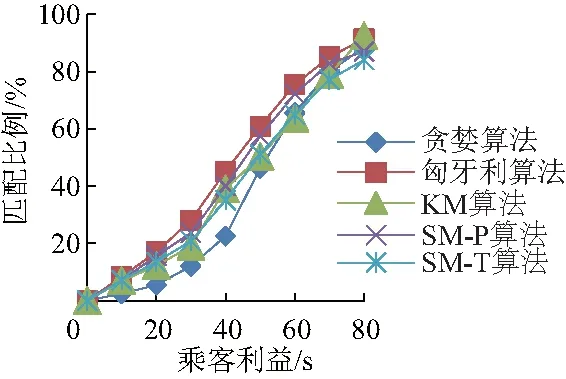
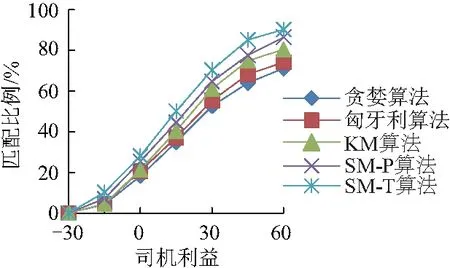
w(rj)值越小乘客利益越高(w(rj)≥0).rj为乘客j的订单任务.D(p(vi),s(rj))为第i个司机当前位置p(vi)与第j个乘客当前位置s(rj)之间的距离，vi为司机i的利益.若D(p(vi′),s(rj))

影响司机利益函数的因素主要有接客路程、订单路程、补贴三项因素.其中接客路程是指司机当前位置与订单出发位置间的距离，司机更偏好于较短的接客路程.订单路程是订单出发位置和目的位置间的最短距离，也是是司机利益的核心部分.为简化司机利益模型，不考虑有关时间的计费和起步价，认为价格与订单路程成正比.补贴是提高订单完成率、促使司机接按常规计费乘客订单的重要因素，且可增加网约司机的收益.定义乘客的订单rj补贴为Allo(rj).

综上，订单路程和补贴是网约车司机的收益，接客路程是成本.考虑到收益和成本对司机利益产生的影响不同，故用两个系数α、β分别为成本和收益对司机利益函数产生影响的不同权重，定义司机的利益函数w(vi)为：

w(vi)=D(p(vi),s(rj))-αD(s(rj),d(rj))-

βAllo(rj)

(2)

w(vi)值越小司机利益越高，司机更倾向选择w(vi)值小的订单任务.D(s(rj),d(rj))表示第j个乘客当前位置s(rj)与目的地d(rj)之间的距离.若D(p(vi),s(rj′))-αD(s(rj′),d(rj′))-βAllo(rj′)

此外，司机对每一单的利益存在阈值θ，司机不会接受低于阈值的订单任务，即w(vi)<θ时，vi拒绝匹配rj.

司机利益不会直接影响乘客利益，但接客距离共同影响了二者的利益函数，使得司机利益与乘客利益潜在相关.即，对于一个潜在的订单任务匹配(rj,vi)，可能乘客对其偏好程度非常高，但司机的偏好程度很低.

1.2 非共享出行模型中任务分配策略

在非共享出行模型中，乘客发起订单，司机接受订单，完成乘行后获得各自的利益.在该模型下通过稳定匹配可实现乘客与司机的最优匹配，稳定匹配结果可保证司机与乘客均获得最优利益达到平衡状态.

1.2.1 稳定匹配策略

在非共享出行模型的订单任务匹配中，通过乘客和司机的偏好矩阵，确定稳定匹配(stable matching, SM)结果，如例1、2.

例1：表1为r1,r2,r33名乘客的订单任务和3位驾驶车辆v1,v2,v3司机的组成的偏好矩阵.

表1 偏好矩阵(例1)

在例1所有可能的订单任务匹配结果中，存在3种稳定匹配结果，分别是：①r1与v1、r2与v2、r3与v3匹配.② 每位司机得到其最佳选择：r1与v3、r2与v1、r3与v2匹配.③ 每位司机都与其第二选择匹配：r1与v2，r2与v3，r3与v1匹配.

例2：表2是r1,r2,r33名乘客的订单任务和3位驾驶车辆v1,v2,v3司机的利益组成的偏好矩阵.

在例2中，存在一种稳定匹配结果，即r1与v1、r2与v2匹配.

表2 偏好矩阵(例2)

通过例1、2的分析，可以得出，在非共享出行模型的订单任务匹配中，总存在一组稳定匹配，并可通过算法1的反复迭代可得到稳定匹配结果，进一步说明了订单任务的稳定匹配必然存在.

算法1给出了一种基于延迟接受的迭代求解订单任务稳定匹配的方法.算法由主程序Dispatch、子程序Proposal、子程序Refusal 3部分构成.程序输入中，dispatch[i]中存放与司机i匹配的乘客.fc[i][j]存放对于司机i而言，乘客j在其序列中的序号，便于在子程序Refusal中进行序列比较.

第1至第18行为主程序Dispatch.第3行至第11行在使用D_choice初始化fc数组.第12至15行初始化p_counter和fc的第一列，此二者相互配合，在迭代过程中记录每个乘客下一个请求对象.第16至18行，依次调用Proposal子程序，确保每个乘客都进行匹配.

第19至26行为子程序Proposal.核心在于获取此次Proposal的对象，若j<0则说明不存在可匹配对象，此次proposal过程终止.

第27至36行为子程序Refusal.用于询问被请求方的司机对于请求匹配的乘客的回应，对司机而言，如果乘客存在更好选择，则进行替换，且被替换的乘客需要进行下一轮Proposal.如果不存在更好的选择，则乘客继续进行Proposal，司机保持匹配对象不变.

算法1的时间复杂度为O(|R||V|).对于每一个司机而言，其均可能拒绝m-1个乘客的请求，直至最后一个司机获得其匹配对象，即请求次数最多为(m-1)(n-1)+1，故时间复杂度为O(|R||V|).因为算法1在多项式时间内可解，故一定存在至少一组稳定匹配.

1.2.2 算法1的实例说明

通过下述实例详细说明算法1的流程.

表3 偏好矩阵(实例)

表3为乘客和司机的偏好矩阵，在表格中用“-”标出r2订单的乘客拒绝匹配驾驶车辆v1的司机，v2的司机拒绝匹配订单r2的乘客.每个乘客或司机对应的偏好序列，从左至右偏好依次下降，即最左端的对象具有最高偏好程度.

图1 实例匹配过程Fig.1 Instance matching procedure

如图1，在初始状态中，司机没有和任何乘客匹配.在r1的请求轮次中，r1与v1暂时匹配.在r2的请求轮次中，r2希望与v2进行匹配，但由于v2的驾驶司机拒绝匹配乘客r2的订单，所以r2顺延至下一位偏好顺序发起请求.但发起订单r2的乘客拒绝匹配v1的驾驶司机，匹配失败，r2的请求轮次结束.在r3的请求轮次中，r3对v1发起匹配请求，因为v1更偏好r3，r3与v1暂时形成匹配.此时r1需要迭代进行匹配请求，向v2发出匹配请求，因为v2暂时没有匹配对象且不拒绝r1，所以r1与v2形成另一对匹配.此时所有司机均获得相应的匹配乘客，匹配过程结束.

1.2.3 非共享出行模型的性质

通过基于延迟接受的稳定匹配算法获得的订单任务匹配结果，实现在非共享出行模型中司机和乘客的利益函数达到平衡状态，此时该匹配结果是最优结果，定义最优订单任务匹配结果如定义1.

定义1：如果在某种匹配策略下，乘客(司机)的收益不小于任何其他匹配策略，则称这种匹配策略是乘客(司机)最优的.

从定义中可知，最优性是指在所有任务的稳定匹配结果中，对于某一集合中的全部成员例如乘客方而言，均可获得最高收益.此外，非共享出行模型的任务匹配结果具有最有唯一性、匹配结果存在性以及排他性.

性质1(最优唯一性)：只存在一种最优匹配策略.

证明：如果存在两种最有匹配策略，假定无平局，此时乘客(司机)在一种分配策略下的收益总大于另一种分配策略下的收益，因此这两种分配策略总有一个不是最优的.故只存在一种最优订单任务匹配策略.

性质2(最优存在性)：基于延迟接受的匹配结果，对于匹配过程的主动方来说，利益不小于任何其他的稳定匹配结果，又因为任务匹配结果的最优唯一性，主动方一定获得最优匹配.

证明：先采用归纳法证明乘客最优.假设初始化时，任意一个乘客没有被拒绝.假设在某一时刻，已经获得匹配对象的司机v1拒绝了乘客r1，且司机v1更偏好乘客r2.假设存在一个匹配方案，把乘客r1匹配给司机v1，乘客r2被分配给了相较于司机v1偏好程度更低的司机.因乘客为r2与司机v1都更想选择对方，因此该匹配结果不稳定.通过归纳法可得，任意司机只拒绝了在任何稳定方案中偏好程度更低的乘客，因此可得乘客最优的匹配结果.同理可得司机最优匹配.

性质3(最优排他性)：在最优稳定匹配中没有获得匹配的乘客，在其他稳定匹配中也不可能被匹配.

证明：M*为乘客最优稳定匹配，rj为M*中没有被匹配的乘客.假设存在另一个稳定匹配M，M≠M*，rj在M中被匹配，M(rj)为在匹配M中rj的匹配对象.根据稳定匹配的定义，相较于rj拒绝匹配的对象，rj必然更偏好M(rj).所以在M*中，M(rj)必然被rj请求匹配过，然而M(rj)在M*并不是rj的匹配对象，这意味着M(rj)在M*中有更优的匹配对象从而拒绝了rj.但是M(rj)在M*中的对象必然比M中的差，这显然存在矛盾.故rj不在M中被匹配.

1.3 全部稳定匹配策略

由性质2可知，通过基于延迟接受的稳定匹配算法时，一定会获得匹配结果.但极少有网约车平台会长期采用该订单任务分配策略，因为这意味着平台设定的被动方必然在每一个匹配过程中收益最低.针对上述问题，文中在稳定匹配的基础上提出了一种全部稳定匹配算法，目标在不确定平台具体利益倾向和策略的情况下，在多项式时间内获得全部订单任务的稳定匹配.为了在算法1稳定匹配的基础上，获得新的匹配，需要通过以下3项规则进行约束.

规则1：给定S和rj，当S(rj)与另一名乘客rj′试图进行匹配，并且S(rj)相较于rj′更偏好rj，此时订单任务匹配成功(具体通过子程序BreakDispatch实现)，否则失败.规则1用以保证算法2的正确性.

规则2：给定S和rj，在调用子程序BreakDispatch的订单任务匹配过程中需要保证乘客请求rj′中j′≥j，此时匹配成功.如果j′

规则3：给定S和rj，如果rj在S中未匹配，那么该轮涉及rj的匹配过程直接结束.规则3用以保证算法2的执行效率.

算法2旨在寻找所有稳定匹配.算法2包含两个部分.第1至4行为主程序All Dispatch，包括调用算法1获得乘客最优稳定匹配(第2行)和对每个订单迭代地调用子程序BreakDispatch以打破现有匹配结果，试图获得新的稳定匹配结果(第3至4行).第5至12行为子程序BreakDispatch，通过打破rj在S中的匹配对，并试图获得新的匹配.BreakDispatch中需要调用算法1中的子程序Proposal和Rufusal.第7至8行，在约定规则下打破现有匹配(rj,S(rj))，因为规则的约束，BreakDispatch可能成功可能不成功.如果成功，则将获得新的匹配S’，将其加入集合S(第10行)，并递归调用BreakDispatch以获得新的稳定匹配.

2 共享出行模型及订单任务分配策略

非共享出行模型只考虑了一个乘客订单和司机匹配的情况，然而在现实情况中，在出行高峰时期难打到车时，人们常常会选择共享出行.基于此，文中建立了共享出行模型，重新定义了共享出行模型下的司机利益函数，乘客利益函数，仍然通过稳定匹配算法获得了订单任务稳定匹配策略结果.

2.1 共享出行订单任务模型

在共享出行订单任务模型下，乘客希望通过与他人拼车，用非共享模型下更多的等待时间和可能延长的订单距离换取更少的花费，而司机通过共享模型可以在同一段路程上搭载多个订单上的乘客，收入较非共享模型下更高.

定义共享出行订单任务模型为一个四元组SM=，其中：

ck={rj1,rj2,…,rjn}为共享一辆网约车的订单集合；

S为出发位置的集合；

W为乘客发起订单获得的利益w(rj)share和司机执行完订单任务后的利益w(vi)share的集合；

Squ为接送顺序的集合.

在共享模型中，目标是找到完成所有订单的最短路径，且最短路径决定了各订单的接送顺序.根据实际打车情况，一辆网约车最多可以同时接受3份订单，约束一辆网约车最多可以同时接受3份订单，即|ck|≤3.

2.2 利益函数

基于非共享出行模型下乘客的利益函数w(rj)和司机的利益函数w(vi)，根据共享出行模型的需求特点，重新定义乘客的利益函数w(rj)share和司机的利益函数w(vi)share.

首先定义司机的利益函数w(rj)share.影响乘客的利益函数的因素与非共享出行模型下的影响因素相同，都为等待时间(接客路程).定义Dck(p(vi),s(rj))为乘客订单rj属于驾驶vi的司机的共享订单集合ck，表示从驾驶vi的司机当前位置到乘客订单rj的出发位置之间的距离.显然，Dck(p(vi),s(rj))是最短路径的一部分.需要注意的是，Dck(p(vi),s(rj))并不是vi的司机当前位置到乘客订单rj的出发位置之间的最短距离，因为在接rj前可能需要接其他乘客.除此以外，与非共享出行模型不同的是，乘客关心其实际行驶距离较订单路径最短路径多出的距离.因为可能先将其他乘客rj′送至其目的位置，对于rj而言，其相较于非共享模型下的最短距离要多(除非rj′就在rj的最短路径上).用Dck(s(rj),d(rj))表示乘客rj从出发位置到目的位置在最短路径的距离.乘客rj多行的距离可以用Dck(s(rj),d(rj))-D(s(rj),d(rj))来表示.故乘客rj在共享出行模型下的利益函数w(rj)share为：

w(rj)share=Dck(p(vi),s(rj))+

θ[Dck(s(rj),d(rj))-D(s(rj),d(rj))]

(3)

其中，θ为系数，表示接客距离和多行距离的比例.w(rj)share值越小意味着rj的偏好程度越高.当|ck|=1时，乘客利益函数w(rj)share变为D(p(vi),s(rj))，此时与非共享出行模型的模型相同.对于共享订单集合ck而言，整个集合的利益等于集合中各成员利益的代数和，即w(ck)=∑w(rj)share,rj∈ck.

与非共享出行模型相似，影响司机利益的因素同样可以归纳为接客距离、订单距离之和、补贴3点，具体为：

(1) 接客距离，Dck(vi)为司机vi与第一个上车乘客的接客距离.

(2) 订单距离之和.司机获得利益与距离之和直接相关.

(3) 补贴.共享订单集合ck的补贴用Allo(ck)表示.

定义司机的利益函数w(vi)share为：

w(vi)share=Dck(vi)-α∑D(s(rj),d(rj))-βAllo(ck)

(4)

当|ck|=1时，司机利益函数w(vi)share变为w(vi)share=D(p(vi),s(rj))-αD(s(rj),d(rj))-βAllo(rj)，与非共享出行模型相同.

同样地，假设存在订单利益阈值θ，定义司机不会接受低于阈值θ的订单，即w(vi)<θ时，vi的司机拒绝匹配发起订单ck的乘客.

2.3 稳定匹配算法

为了在共享出行模型中获得订单任务稳定匹配结果，基于非共享出行模型的稳定匹配算法，将稳定匹配算法划分为打包和匹配两个步骤：

步骤1：根据乘客订单的偏好程度进行打包至可行子集；

步骤2：乘客请求的每个子集都被视为非共享出行模型下的单独调度的乘客订单.即先最大化打包共享出行模型下的稳定匹配问题中的订单，后求解稳定匹配策略.

因为打包的订单被整体看做一个非共享出行模型下的新订单，所以步骤2中求解稳定匹配的过程与算法1的过程相同，在此不做赘述.

定义C={ck}表示共享乘车的乘客请求的所有可行子集的集合.根据实际情况限定ck集合的大小为2≤|ck|≤3，可通过穷举搜索计算获得所有可行的ck.步骤1的目标是最大限度地打包乘客订单到可行的子集，用布尔变量xk表示ck是否成功打包，目标函数是最大化乘客订单：

(5)

xk∈{0,1}

3 实验与分析

文中实现了非共享出行模型及共享模型中的稳定匹配算法，把稳定匹配算法在纽约市出租车数据集TCL数据集进行了模拟实验，并与其他主流订单任务分配算法在匹配延迟时间、乘客利益、司机利益等评估指标进行了比较与分析.

3.1 数据集及相关设定

文中选用的是纽约市出租车数据集TCL，对2019年03月14日收集的绿色出租车行车记录，共20 929条记录进行了整理.由于数据集提供的数据内容有限，假设共有500辆出租车提供服务，出租车的初始位置遵循从市中心向外围的二维正态分布，网约车系统的时间窗口为10 s.

3.2 比较算法和评价指标

把非共享出行模式下稳定匹配算法的订单任务结果记为SM-P，把共享出行模式下稳定匹配算法的订单任务结果记为SM-T.其中参数α=1,β=0.为验证文中所提模型的有效性和可行性，把3种算法与文中的稳定匹配算法进行比较：

(1) 贪婪算法.将最近的空闲出租车发送给乘客订单进行匹配.

(2) 改进的匈牙利算法.乘客请求和出租车之间的距离是匹配成本，该算法目标为求得最小成本的匹配.

(3) KM算法.其中乘客利益和司机利益的比例系数为1，即α=1.该算法的目的在于最大化系统整体利益.

为对比上述算法的性能，采用3个评价指标：

(1) 匹配延迟时间.从乘客请求发送到系统，系统进行匹配后将结果发送给该乘客之间的延迟时间.

(2) 在非共享出行模型下和共享出行模型下的乘客利益.

(3) 在非共享出行模型下和共享出行模型下的司机利益.对于3个指标，值越小说明算法的性能更优.

3.3 结果及分析

如图2，对于所有的算法，超过75%的乘客请求会在一个时间窗口内获得订单匹配结果.相较而言，匈牙利算法的调度延迟较小，文中所提稳定匹配算法在两种出行模型下延迟时间均稍长一些.贪婪算法在第一个时间窗口中获得匹配的比例最低，而随着延迟时间增长，其增长速度明显有快速提高.但在时效内不能得到匹配结果的匹配策略会导致乘客取消订单，故调度延迟应在时效范围内.

图2 匹配延迟时间Fig.2 Matching delay time

图3为乘客利益及其比例.从整体上看，匈牙利算法和非共享出行模型下稳定匹配算法SM-P的乘客利益更高，原因是匈牙利算法的权重是客请求和出租车之间的距离，优先考虑了乘客的利益；而非共享出行模型只考虑了一个乘客的订单需求，且通过稳定匹配算法获得最优利益，因此乘客的利益更高.而KM算法和在共享出行模型中的算法结果SM-T的表现整体较差，因为KM算法中乘客利益和司机利益的比例系数设为1，导致利益不偏向任何一方.而共享出行模型中的算法结果SM-T表现较差的原因是在共享出行模型中，会折衷部分乘客的利益实现共享出行.

图3 乘客利益Fig.3 Passengers utilities

贪婪算法中获得高利益的比例非常低，而在利益中间值附近有一个很大程度的提高，说明大部分乘客的利益都落在这个利益中间值附近.贪婪算法具有一定随机性，该结果符合在各个指标上的表现的预期.

图4展示了司机利益及其比例，匈牙利算法、非共享出行模型下稳定匹配算法结果SM-P、KM算法和共享出行模型中的算法结果SM-T的表现与它们在乘客利益上的表现正好相反，符合预期.若重视司机利益必然导致乘客利益受损.贪婪算法的结果显然明显低于其他所有算法，因为贪婪算法是一个近似随机的算法，其他算法在不同程度上保证了司机的利益.

图4 司机利益Fig.4 Drivers utilities

4 结论

(1) 在非共享出行模型中，建立了乘客和司机的利益函数，提出了基于延迟接受思想的迭代算法，获得订单任务的最优稳定匹配结果.同时，证明了该算法的最优唯一性和最优存在性等3个重要性质.

(2) 为考虑平台具体利益倾向和策略的情况基于稳定匹配算法，提出了一种通过打破现有稳定匹配对的方法以获取全部稳定匹配，进一步提高稳定匹配效果.在共享出行模型中，同样建立了乘客和司机的利益函数，在该模型下的稳定匹配问题可通过最大集合打包问题和任务匹配两个步骤进行.

(3) 通过模拟实验实现了文中在非共享出行和共享出行下的稳定匹配算法，并在数据集TCL进行模拟实验，从匹配延迟时间、司机利益、乘客利益等3个评估指标与其他主流算法进行比较与分析，说明所提模型的有效性和可行性.

(4) 研究了基于稳定匹配的订单任务分配策略，为解决利益平衡问题奠定了理论基础.但所提模型尚未考虑在策略决策方有动机最大化利益时的可行性，因此在未来的研究工作中，需要进一步研究：① 将基于稳定匹配的订单任务分配策略作为一种分配策略框架，在该框架下提高各方利益.② 根据具体利益倾向设计对应算法，例如最小化遗憾成本、最小化平等成本等，当利益与之匹配时，设计相应的求解算法.