潜深对近水面潜体与自由液面耦合作用的影响

朱信尧，韩 月，朱仁庆，王树齐

(江苏科技大学 船舶与海洋工程学院，镇江 212100)

海洋中蕴含着丰富的资源，水下潜器及船舶是海洋开发的重要手段.微小型水下潜器绝大部分时间在深水中工作，但当其从水面搭载平台布放和回收、航行一段时间后上浮进行导航定位及传输数据时，潜体受到自由液面影响.小水线面双体船的水下潜体一般为回转体，而其离自由液面很近[1].当潜体在近水面附近运动时，潜体会与静水面之间有显著的相互作用，水面会发生明显的变形，不再为静水面，甚至可能会在水面上出现波浪破碎等现象，自由液面对潜体受力造成明显影响.

文献[2-6]利用STAR-CCM+对DARPPA SUBOFF AFF-1(裸艇体)模型轴线距自由液面高度(潜深)h从1.1倍最大直径D到∞、无量纲速度Fn从0.205到0.512、侧滑角β从0到18.11°时的流场进行了模拟，分析了自由液面及粘性对潜体受力、操纵性的影响；文献[7]对SUBOFF有/无附体潜艇模型无量纲速度Fn从0.128～0.84、无量纲深度h/D为1.3、2.2、3.3、4.4时的流场进行了模拟并分析了附体对近自由液面潜体受力的影响；文献[8]研究了SUBOFF模型无量纲速度Fn从0.3～0.5、无量纲深度h/D为1.1、2.2、3.3、4.4时与自由液面的相互作用；文献[9-10]利用ANSYS CFX及STAR-CCM+对Afterbody-1模型潜深h/D从0.75到4.0、速度从0.4 m/s到1.4 m/s时的流场进行了模拟并分析了自由液面对潜体受力的影响；文献[11]利用CFD方法对回转体Afterbody-1模型的流场进行了模拟，研究了潜深、速度等对潜器近水面受力的影响；文献[12]利用CFD方法对一鱼雷状水下潜器在潜深h/D为1.5、2.5、3.5三种工况下的流场进行了模拟，研究了近水面航行器的水动力性能；文献[13]利用泰勒展开边界元法对近水面潜艇迎浪状态下的垂向二阶波浪力进行了计算.

国内外学者研究潜体与自由液面耦合作用时潜深h/D一般取值较大，对h/D为0.5～0.75的研究很少.文中基于CFD理论，利用重叠网格方法对DARPPA SUBOFF裸艇体模型h/D从0.5到3.3时的流场进行模拟，研究潜深对近水面潜体与自由液面耦合作用的影响.

1 数值方法

采用雷诺时均N-S方程方法(RANS，Reynolds Averaged Navier-Stokes equation)求解潜体近水面粘性流动问题.主要求解模型设置为:

(1) 湍流模型采用SSTk-ω湍流模型；

(2) 自由液面捕捉采用VOF方法；

(3) 采用瞬态分析，时间步长设置为0.01 s；

(4) 耦合方式：压力速度耦合方式采用Coupled耦合求解方式；

(5) 离散方式：压力采用PRESTO！离散方式；体积分数采用compressive离散方式；动量采用Second Order Upwind离散方式；

(6) 收敛监视：采用RMS残差监视方式，残差值取10-6；以迭代时所监测力恒定或成周期性的变化作为收敛与否的判定标准.

2 几何模型、计算工况及网格划分

2.1 几何模型

以DARPPA SUBOFF AFF-1为研究对象[16]，模型的主要参数如表1，模型三维图如图1.

潜深h与艇体最大直径D之间的比值定义为h*，即h*=h/D.

表1 SUBOFF模型主要参数

图1 DARPPA SUBOFF AFF-1模型

2.2 计算工况

为了研究潜深对近水面潜体与自由液面耦合作用的影响，文中对SUBOFF模型在傅汝德数Fn为0.205、0.359、0.512，潜深h*为0.50、0.55、0.60、0.65、0.70、0.75、0.80、0.90、1.00、1.10、2.20、3.30时共36种工况下的流场进行模拟.傅汝德数Fn为0.205、0.359、0.512时速度分别为1.248 621、2.186 61、3.118 508 m/s.

2.3 网格划分

对于潜体近水面水动力计算这类绕流问题，一般通过建立一个适当的虚拟边界，将绕流问题转化为内流问题，在虚拟边界与潜体形成的空间区域内求解RANS方程.外围流场采用长方体区域的形式，其计算域边界条件及尺寸如图2.由于流场关于纵剖面对称，为了提高计算精度、减小计算时间，所选计算域为关于纵剖面xoz对称的一半区域.

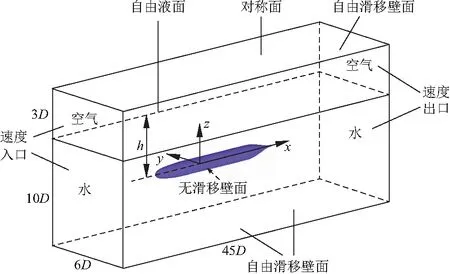
图2 计算域Fig.2 Computational domain

由于结构化的网格便于调整网格疏密、便于处理边界层的网格并能够提高数值仿真结果的精度，文中采用结构化的六面体网格形式.

当潜深h*为0.5时，潜体上表面与自由液面相切，为了保证此时的网格质量，采用重叠网格的方法进行网格划分.

(1) 部件网格

部件网格为SUBOFF周围区域的网格，其区域从为11D，头部前面为1D，直径为1.6D.对其流域划分结构化网格，当速度为3.118 508 m/s时，为了保证第一层边界层y+在30～120，第一层网格尺寸取0.7 mm.SUBOFF周围重叠网格如图3.网格数量为78万，网格质量都大于0.36，质量较高.

图3 重叠网格

(2) 背景网格

背景网格区域取长45D、高13D、半宽6D.对其流域划分结构化网格，在自由液面上下各0.2 m加密，垂向网格尺寸为0.01 m.背景网格如图4.网格数量为102万，网格质量都大于0.97，质量很高.

图4 背景网格Fig.4 Background mesh

3 计算准确性研究与验证

3.1 网格收敛性研究

以划分的网格参数为基准，对SUBOFF AFF-1模型无限水深0攻角及潜深h*为1.1时网格的收敛性进行研究，计算工况及网格参数如表2.

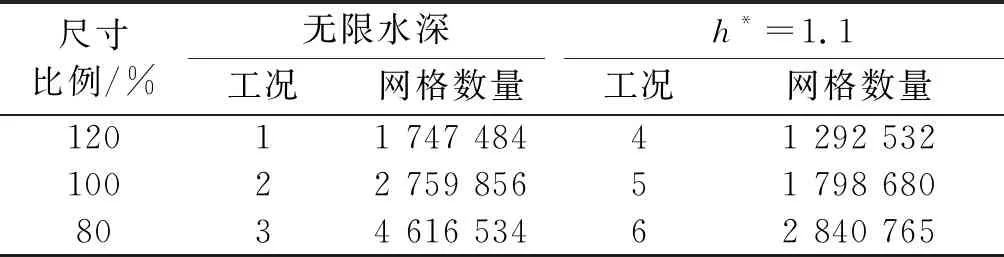
表2 网格收敛性研究网格参数

阻力系数CT、升力系数CL及俯仰力矩系数my计算公式分别为：

(1)

(2)

(3)

式中：Fx,Fz,My分别为阻力、升力及俯仰力矩；ρ为水的密度；v为潜器速度；Ω及L为潜器的湿表面积及长度.

为了与文献[17]中试验结果对比，无限水深0攻角计算速度取3.045 248 m/s，计算结果如表3，结果随网格变化如表4.

表3 无限水深计算结果

表4 无限水深计算结果随网格变化百分比

为了与文献[2]中试验结果对比，潜深h*=1.1时计算速度取3.118 508 m/s，阻力收敛曲线如图5，从图5可以看出，120 s后阻力波动很小，说明此时已经收敛，结果处理时取120 s后的平均值.计算结果如表5，结果随网格变化如表6.

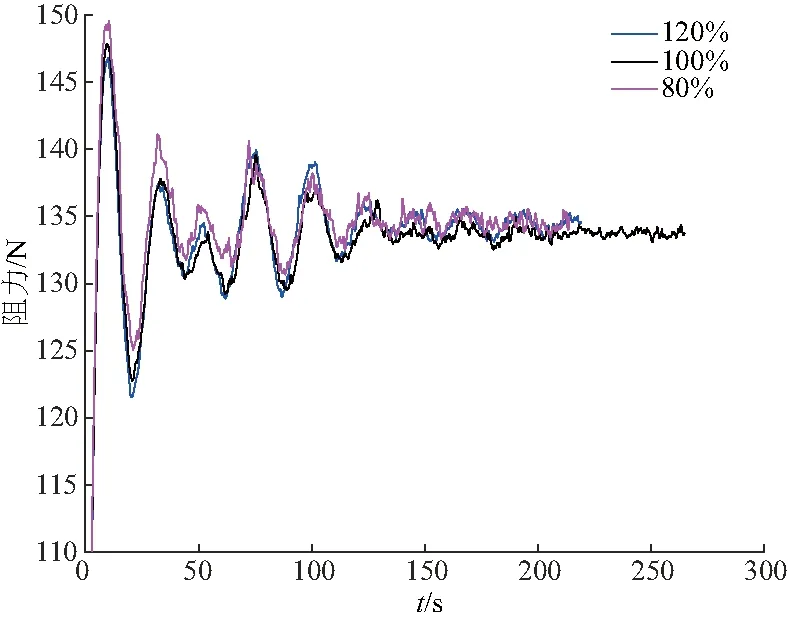
图5 h/D=1.1时阻力收敛过程曲线Fig.5 Drag convergence curve of h/D=1.1

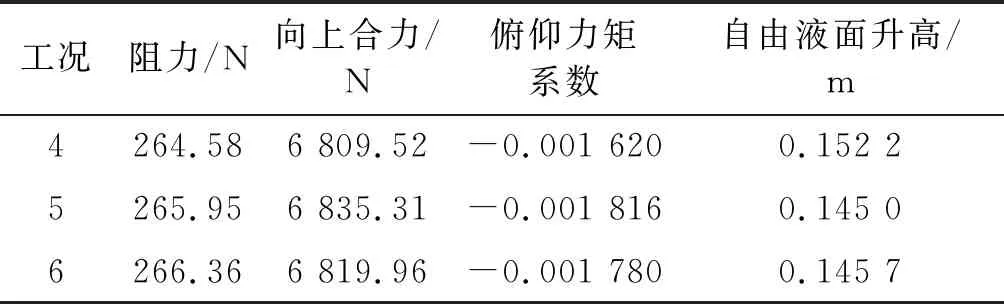
表5 潜深h*=1.1时计算结果

表6 潜深h*=1.1时计算结果随网格变化百分比

从表4可以看出，无限水深时，工况2-3时结果变化仅为-0.16%；再增加网格密度，对计算机硬件要求太高，计算时间更长，且对结果影响很小，所以网格尺度达到工况2时已经满足精度要求；

从表6可以看出，潜深h*=1.1时，除去俯仰力矩系数外，工况5-6时结果变化均小于0.5%；俯仰力矩系数变化较大的主要原因是俯仰力矩系数本身就是一个很小的量，导致求解时相对变化较大.

综合考虑计算时间及计算结果的稳健性，文中计算时取比例为100%的网格进行计算分析.

3.2 计算准确性验证

为了验证求解的精度及可信性，采用文中计算方法对DARPPA SUBOFF AFF-1模型无限水域及近自由液面的流场进行了模拟，并将计算阻力与试验结果进行了比较.

(1) 无限水域

利用2.3划分的网格，对SUBOFF AFF-1模型0攻角情况下的流场进行了模拟，得到其阻力并与文献[17]中试验结果对比如表7.

从表7可以看出，文中CFD计算阻力系数和试验结果相差小于2.89%，精度很高.

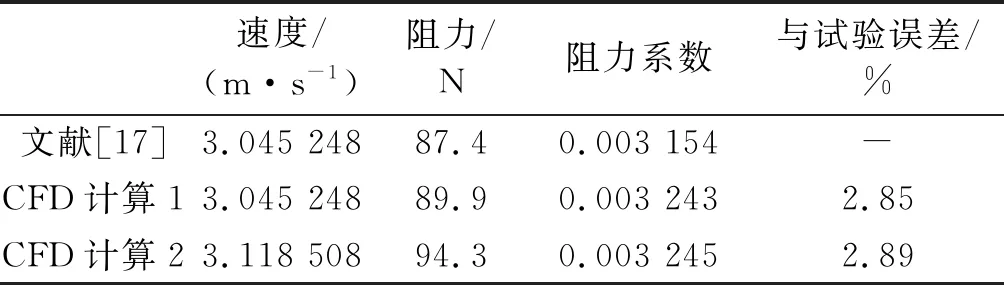
表7 无限水域准确性验证比

(2) 近自由液面

利用划分的网格，对SUBOFF AFF-1模型轴线距自由液面距离h为1.1D、2.2D、3.3D情况下0攻角时傅汝德数Fn为0.512时的流场进行模拟.

图6为潜器纵剖面底部y+值沿x方向的变化.文中计算所得阻力与文献[2]中试验结果对比，如表8.

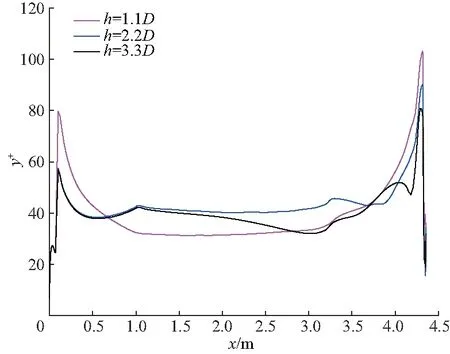
图6 潜器纵对称面底部曲线y+Fig.6 y+ of the bottom line of SUBOFF

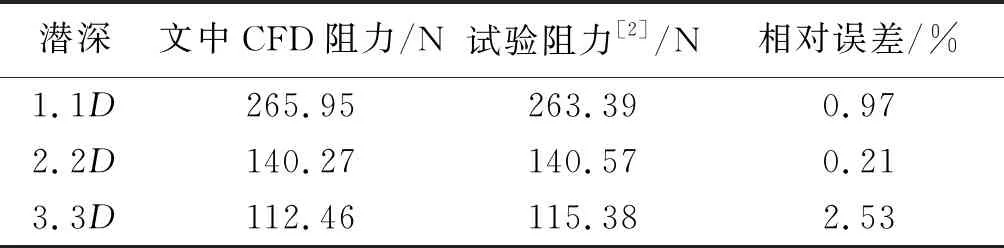
表8 近自由液面准确性验证

从图6可以看出，y+在30～110，适合对潜器流场进行求解.

从表8可以看出，文中近自由液面CFD计算阻力与试验相比误差在2.53%以内，精度很高，满足计算精度要求.文中CFD计算结果精度很高的主要原因是网格划分方式采用结构化网格，并对潜器边界层网格及自由液面网格进行了加密，网格更加细致.

4 结果与分析

文中数值模拟了Fn分别为0.205、0.359、0.512时，潜深h*为0.50、0.55、0.60、0.65、0.70、0.75、0.80、0.90、1.00、1.10、2.20、3.30时共36种工况下的流场.文中对近水面潜体与自由液面耦合作用的阻力、升力、俯仰力矩及自由液面情况进行了总结分析.

4.1 阻力

Fn分别为0.205、0.359、0.512时潜器总阻力系数CT随无量纲潜深h*的变化曲线如图7.

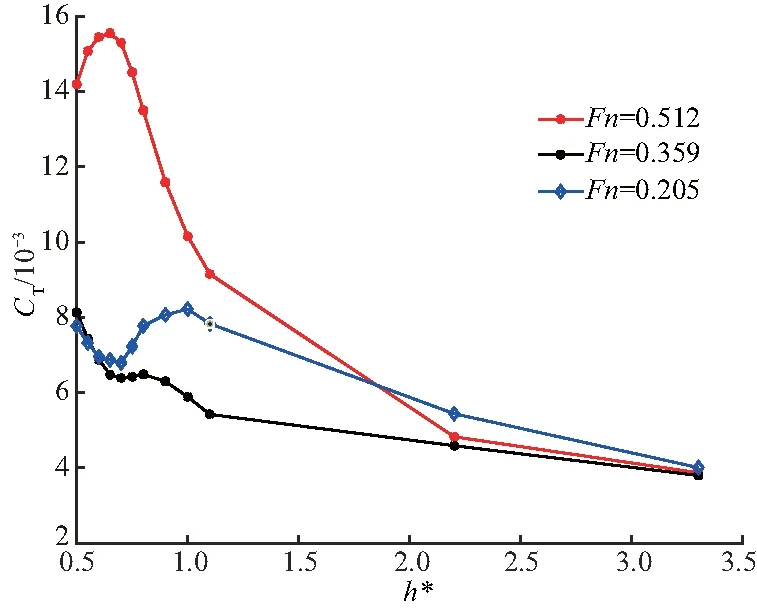
图7 总阻力系数随潜深的变化曲线Fig.7 Total drag coefficient over depth

潜器所受总阻力可以分为粘性摩擦阻力及剩余阻力，为了便于分析自由液面对阻力的影响，将总阻力系数CT分为摩擦阻力系数Cf及剩余阻力系数Cp，其关系为：

CT=Cf+Cp

(4)

将近自由液面时的总阻力系数CT减去无限水深时的总阻力系数CT∞可以得到由于自由液面影响而产生的阻力系数，即兴波阻力系数Cw，其关系为：

Cw=CT-CT∞

(5)

无限水深时的总阻力系数CT∞可由CFD计算得到，其阻力系数如表9.Fn=0.205、0.359、0.512时不同水深时潜器所受的总阻力系数CT、摩擦阻力系数Cf、剩余阻力系数Cp及兴波阻力系数Cw结果如表10.

表9 无限水深阻力系数

表10 近水面阻力系数结果

从图7及表9、10可以看出，当潜深h*从0.50增大到3.3时：

(1) 当潜器高速航行时(Fn=0.512)，总阻力系数先增大后减小，在潜深h*为0.65时有最大值，其值为无限水域阻力系数的4.79倍；

(2) 当潜器航速中等时(Fn=0.359)，总阻力系数呈先减小后增大再减小的趋势，在潜深h*为0.80时有极大值，其值为无限水域阻力系数的1.85倍；最大值发生在h*为0.5时，其值为无限水域阻力系数的2.32倍；

(3) 当潜器低速航行时(Fn=0.205)，总阻力系数变化趋势与航速中等时类似，也先减小后增大最后减小，在h*为1.00时有最大值，其值为无限水域阻力系数的2.34倍；当h*为0.5时，其值为无限水域阻力系数的2.21倍；

(4) 3种航速下摩擦阻力系数变化均较小，说明潜深对摩擦阻力影响较小；

(5) 兴波阻力系数：① 兴波阻力受自由液面影响很大，其变化趋势与总阻力变化趋势几乎一致，并非离自由液面越近，兴波阻力越大；总阻力增加主要是由于兴波引起的；② 当潜深h*为3.30时，兴波阻力占总阻力的比例非常小，在Fn=0.205时为3.08%，在Fn=0.359时为7.62%，在Fn=0.512时为16.14%；③ 当潜深h*距自由液面很近时，兴波阻力占总阻力的比例变的很大，在Fn=0.205时，兴波阻力占总阻力的比例最大值出现在h*为1.00时，其比例为52.74%；在Fn=0.359时，最大值出现在h*为0.50时，其比例为56.87%；在Fn=0.512时，最大值出现在h*为0.65时，其比例为79.14%.

4.2 升力

文中升力为潜器垂直方向上的所有力的合力，其由水动升力与静水浮力的和减去重力所得.为了保证深水时潜器处于零浮力状态，重力与潜器完全浸没在水中时的静水浮力数值相等.

傅汝德数Fn为0.205、0.359、0.512时潜器升力随无量纲潜深h*的变化曲线如图8.

图8 升力随潜深的变化曲线Fig.8 Lift over depth

从图8可以看出，当潜深h*从0.50增大到3.3时：

(1) 潜器升力总体呈先增大后趋于0的趋势.在h*较大时，潜器距自由液面较远，受自由液面影响较小，由于SUBOFF潜器为回转体，故其升力在0附近；而当h*较小时，其离水面较近，出现明显的露背现象，导致升力减小.

(2) 当潜深h*较小时，速度越高，潜器升力受自由液面影响越大.当潜深h*为0.5、Fn=0.512时潜器所受升力与Fn=0.205时相差444.7 N.

4.3 俯仰力矩

傅汝德数Fn为0.205、0.359、0.512时潜器俯仰力矩系数随无量纲潜深h*的变化曲线如图9.

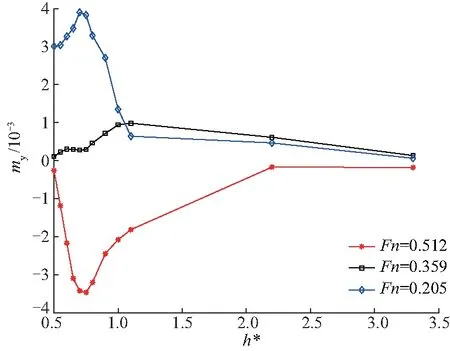
图9 俯仰力矩系数随潜深的变化曲线Fig.9 Pitching moment coefficient over depth

从图9可以看出，当潜深h*从0.50增大到3.3时，俯仰力矩系数绝对值先增大后趋于0.在h*较大时，潜器距自由液面较远，受自由液面影响较小，由于SUBOFF潜器为回转体，故其俯仰力矩系数在0附近；而当h*较小时，其离水面较近，受自由液面影响较大.

潜深h*为0.8时，潜器升力系数、俯仰力矩系数沿潜器轴向分布曲线如图10.Fn=0.512时，潜器升力系数、俯仰力矩系数沿潜器轴向分布曲线如图11.潜器浮心纵向位置距头部2.008 6 m，从图10、11可以看出，潜器产生俯仰力矩主要是由于升力分布不均引起的.

图10 潜深h*为0.8时升力系数、俯仰力矩系数沿潜器轴向分布Fig.10 Distribution of the lift coefficient and pitching moment coefficient along the length of the SUBOFF at the submergence depth h*=0.8

图11 Fn=0.512时升力系数、俯仰力矩系数沿潜器轴向分布Fig.11 Distribution of the lift coefficient and pitching moment coefficient along the length of the SUBOFF at Fn=0.512

4.4 自由液面

潜器近水面航行时，自由液面最大波面升高A与艇体最大直径D的比值定义为A*，即A*=A/D.

傅汝德数Fn为0.205、0.359、0.512时自由液面最大波面升高A*随无量纲潜深h*的变化曲线如图12.

傅汝德数Fn为0.512时潜器纵对称面波形图如图13，潜深h*为0.8时潜器纵对称面波形图如图14.

Fn为0.512时，潜深h*为0.5、0.8、1.1及3.3时潜器纵对称面动压分布云图分别如图15.

图12 无量纲最大波面升高随潜深的变化曲线Fig.12 Normalized maximum wave height over depth

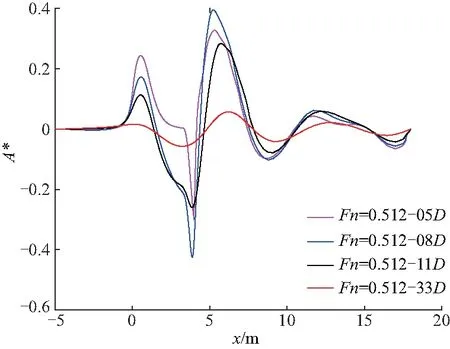
图13 Fn=0.512时潜器纵对称面波形Fig.13 Wave pattern on longitudinal plane at Fn=0.512

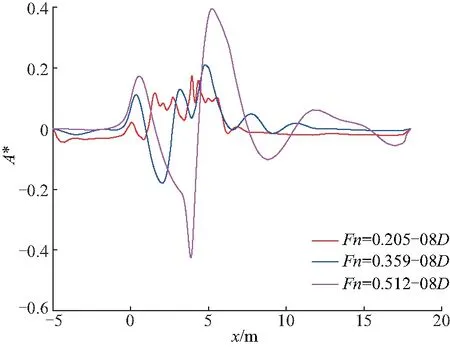
图14 潜深h*为0.8时潜器纵对称面波形Fig.14 Wave pattern on longitudinal plane at h*=0.8

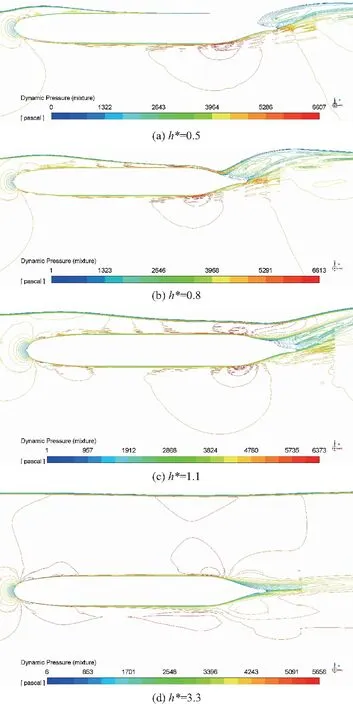
图15 Fn=0.512时潜器纵对称面动压分布云图Fig.15 Distribution of the dynamic pressure on longitudinal plane at Fn=0.512

对自由液面兴波进行分析，可以得到以下结论：

(1) 从图12可以看出，无量纲最大波面升高A*总体呈先增大后减小的趋势，在h*在0.80左右时有最大值.速度为Fn=0.512时最大波面升高达到了潜器直径D的0.4倍.当潜深h*从0.80增大时最大波面升高减小的主要原因是潜器离自由液面越远，受自由液面影响越小，产生的兴波越小；当潜深h*从0.50增大到0.80时最大波面升高增大的主要原因是潜器近水面兴波的最大波面升高并不是发生在头部附近，而是发生在尾流场，当h/D为0.50时，潜体上表面与静水自由液面相切，上面流体较少，导致对尾部流场影响较小，最大波面升高相对较小，此从图13、14、15可以看出.

(2) 从图12、14可以看出，相同潜深时，速度越大，自由液面升高越大，说明速度越大，潜器对自由液面作用越明显；

(3) 从图13、14、15可以看出，潜器近水面兴波的最大波面升高并不是发生在头部附近，而是发生在尾流场；

(4) 从图13、14可以看出，兴波波长受速度影响较大，受潜深影响较小.

兴波理论中波长λ与速度U的关系为[3]：

(6)

从图13、14可以看出，在Fn=0.512时，不同潜深时产生的波长均在6 m左右；在Fn=0.359时，产生的波长约为3 m；在Fn=0.205时，产生的波长约为1 m；此波长计算结果与兴波理论中波长结果一致.

5 结论

当潜深h*从0.50增大到3.30时：

(1) 阻力：当潜器高速航行时，总阻力系数先增大后减小，当潜器中、低速航行时，总阻力系数呈先减小后增大再减小的趋势；自由液面对潜器总阻力影响很大，各速度下最大阻力系数是其无限水深时的2.32～4.79倍；随着潜深的变化，摩擦阻力变化很小，而兴波阻力变化很大；兴波阻力变化趋势与总阻力的几乎一致；总阻力增加主要是由于兴波产生的.

(2) 升力：潜器升力总体呈先增大后趋于0的趋势；而当潜深h*较小时，其离水面较近，出现明显的露背现象，导致升力减小，此时，速度越高，潜器升力受自由液面影响越大.

(3) 俯仰力矩系数绝对值先增大后趋于0.

(4) 无量纲最大波面升高A*先增大后减小，在h*在0.80左右时有最大值；相同潜深时，速度越大，自由液面升高越大；潜器近水面兴波的最大波面升高并不是发生在头部附近，而是发生在尾流场；自由表面兴波波长受速度影响较大，受潜深影响较小.