分离式冲击-刮切复合钻头破岩机理及钻进破岩研究

蔡 灿，谭政博，玄令超，杨迎新，任海涛,2，蒲治成，张 沛，谢 松

(1．西南石油大学 机电工程学院 岩石破碎学与钻头研究所，成都 610500；2.西南石油大学 油气钻井技术国家工程实验室钻头研究室，成都 610500；3.西南石油大学 油气藏地质与开发国家重点实验室，成都 610500；4.中国石化石油工程技术研究院，北京 100101)

随着油气勘探开发的不断深入，深井、超深井不断增多，深部地层的机械钻速降低，钻具的磨损加剧，严重影响了油气田开发的速度和成本。对于钻井工程中常用的PDC钻头，在深部地层仍存在黏滑、回弹震荡等问题，这些问题将导致钻具寿命以及钻井效率降低。

为解决常用PDC钻头在深井、超深井等硬岩钻井过程中出现的问题，逐步发展出轴向冲击、周向冲击以及复合冲击等多种冲击破岩理论与钻具。例如，美国阿特拉公司[1]较早研发了扭力冲击器，采用钻井液涡轮驱动冲击锤产生高频扭转冲击，应用表明，扭力冲击器配合PDC钻头一起使用提高机械钻速效果显著。随后，国内外学者及相关单位特别关注冲击器研究及应用。Powell等[2]提出了一种新的能量分配系统，通过机械升降作用使钻头钻压迅速变化，通过机械撞击产生轴向冲击脉冲，使得钻井时间减少了50%。玄令超等[3]设计了一种新型旋转冲击破岩试验装置，利用齿型振套的碰撞产生冲击载荷，用地质钻机带动钻头破岩。李显义[4]提出了扭转冲击破岩钻井新技术，现场应用结果显示，所设计的扭力冲击器能够显著提高PDC钻头的机械钻速，降低钻进成本。Mu等[5]提出了一种新的轴向-扭转复合冲击钻井工具。贾红军等[6]将冲击钻井破岩技术与脉冲射流辅助破岩技术相结合，研制出一种新型高频低幅扭转振荡耦合冲击器。刘宇[7]设计了一种新型的机械式冲击器，将旋转运动转换为往复运动，使冲击锤产生冲击载荷。柳贡慧等[8]提出了一种适用于软硬交错及非均质性严重地层的复合冲击破岩钻井新技术，通过将轴向脉动冲击与扭向反转冲击破岩方式联合起来，将流体能量转换成扭向和轴向交替的高频冲击机械能。

基于冲击器的研究基础，国内外专家学者对于冲击器作用下的钻头冲击破岩机理也开展了大量的研究。蔡灿等[9]通过分析单齿冲击破碎的齿坑外观形貌图，提出了岩石破碎的分区模型，得出其中潜在破碎区虽然没有破碎，但是岩石已经在应力波的作用下产生了损伤。李思琪等[10]研究了高频谐振冲击破岩的提速效果，发现高频谐振冲击破岩扩大了岩石的响应范围和载荷的作用区域，加剧了岩石振动的剧烈程度。祝效华等[11]研究了扭转冲击作用下切削齿切削岩石过程中的裂纹扩展、岩屑形成、损伤演化以及破岩比功等问题。得出扭转冲击破岩的破碎比功更小，且扭转冲击载荷的幅值存在最优值。刘书斌等[12]建立了冲击-切削破岩分析模型，探究了多维冲击提高PDC钻头破岩效率的机理。李玮等[13]基于振动学理论，在考虑岩石重力的情况下，建立钻头冲击载荷下岩石振动响应的数学模型，采用重整化方法对其求解，分析各参数对钻头高频冲击下岩石振动的影响。方金[14]对冲击载荷作用下软岩的破碎规律展开研究，从理论上分析了冲击载荷作用下软岩的损伤累积过程以及裂纹扩展情况。

上述冲旋钻井中，PDC钻头既存在轴向或者周向冲击，又存在旋转切削运动。这种切削和冲击复合载荷极易导致PDC切削齿过早失效，降低切削齿寿命和钻井效率。因此，杨迎新等[15-16]提出了新型分离式冲击-刮切复合钻头，如图1所示。该钻头由含冲击齿的冲击模块和传统PDC钻头固定刀翼组成，使得复合钻头冲击模块和固定刀翼各自分别独立完成切削破岩与冲击破岩，形成复合破岩效果，也实现了保护PDC齿和提高钻头钻进破岩效果的目的。相比原有PDC-牙轮复合钻头，由于常规牙轮钻头存在牙轮轴承系统，原有复合钻头的可靠性有赖于牙轮轴承和密封系统的使用寿命。而该新型分离式冲击-刮切复合钻头未采用牙轮切削结构，故不存在轴承失效和润滑油密封问题。由于该复合钻头的冲击-切削复合破岩机理和钻进破岩特点尚不清晰，为此采用试验与数值仿真分析分别开展了单齿冲击、单齿切削以及复合破岩钻进研究，以期为新型冲击-刮切复合钻头的设计提供参考。

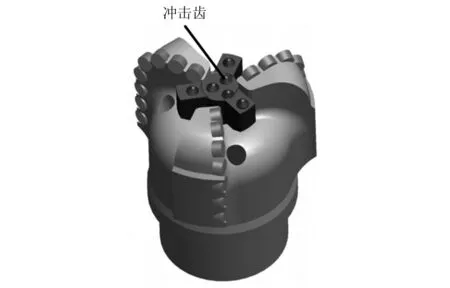
图1 新型分离式冲击-刮切复合钻头Fig.1 New impact-cutting compound drill bit

1 冲击-刮切复合破岩试验装置

为探究冲击-刮切复合破岩以及为数值模型提供验证，设计了先冲击、后切削的试验方案。试验主要分为两个步骤：①先采用冲击齿在岩石上冲击形成冲击坑；②然后利用单齿切削试验平台以不同的切削路径偏离冲击坑距离切削含冲击坑岩样，试验装置示意图如图2所示，由应变采集系统采集切削力[17-18]，传感器接头固定在刀头架上，PDC切削齿以及配套齿座安装于刀架下方，通过螺钉固定，PDC切削齿切削角及侧倾角均可调节。岩石通过夹持装置固定于切削平台上，进行单齿切削试验时，由切削平台带动岩石进行直线切削运动。

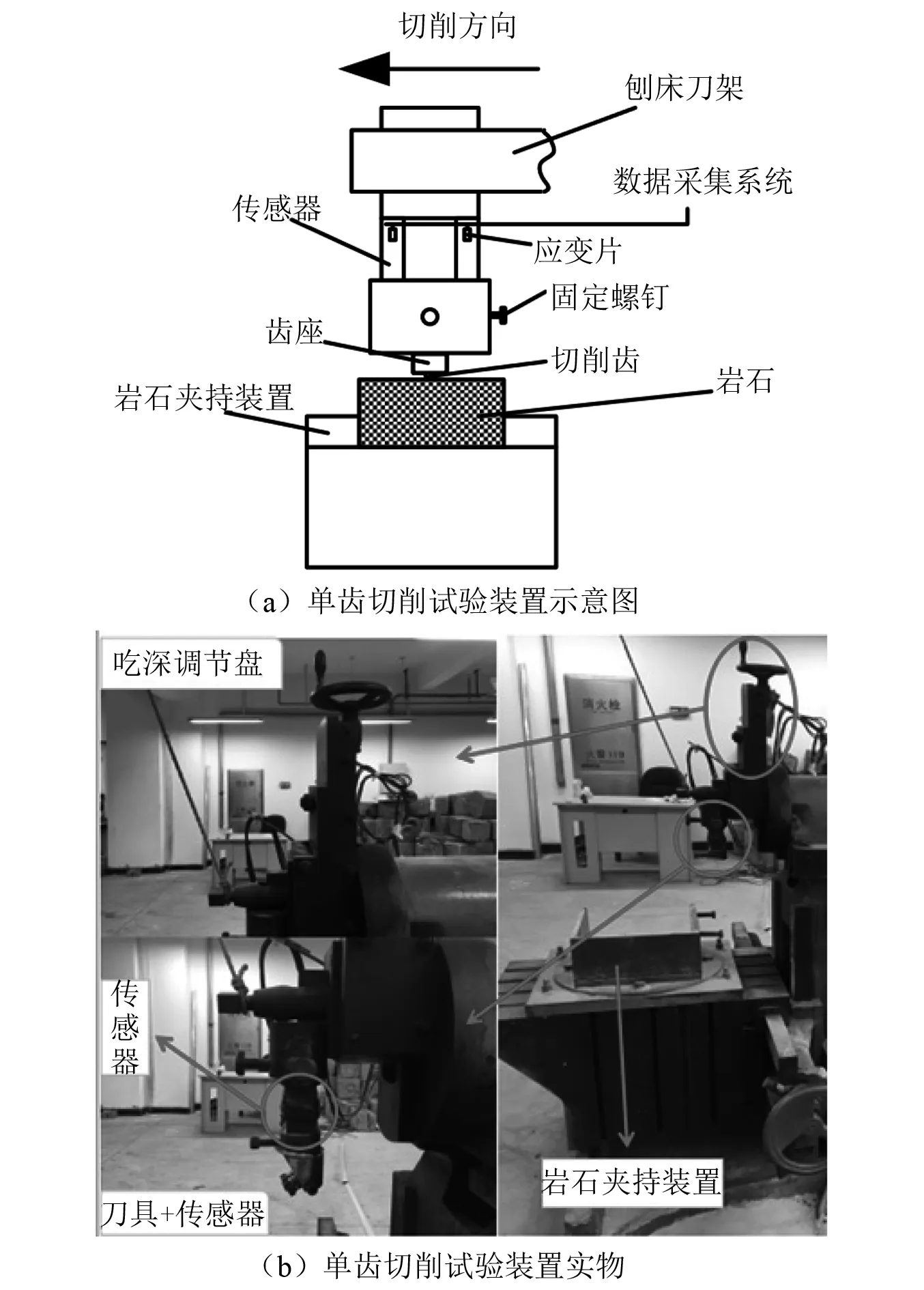
图2 单齿切削试验装置示意图及实物Fig.2 Schematic diagram and physical object of single tooth cutting experimental device

2 有限元建模及研究方案

2.1 三维模型建立

由于单个PDC切削齿的切削深度较小，旋转切削一圈产生偏离轴线的角度很小，故将单个PDC切削齿的旋转切削简化为切削固定深度的直线运动，并且做出如下假设：①岩石为连续、均质、各向同性的材料；②忽略温度对其的影响；③岩石单元一旦发生失效，立即删除，同时忽略失效的岩石单元对后续切削过程的影响。

岩石本构模型采用线性Druker-Prager模型，它同时兼顾了围压对屈服特性的影响，以及剪切引起膨胀的性质。其屈服面不再是标准的圆形，屈服面对应的函数为

F=t-ptanβ-d=0

(1)

式中:p为静水压力；β为摩擦角；d为各项硬化参数，是屈服面在p-t应力空间上的截距；t为替换Mises应力函数中的q的参数，即

(2)

式中:k为流应力比；r为偏应力不变量；q为广义偏应力。

采用有限元方法模拟分离式冲击-刮切复合破岩试验过程，建立的仿真模型如图3所示。其中PDC切削齿直径为15.875 mm，冲击齿的直径为14 mm，切削深度为2 mm。岩石模型为150 mm×125 mm×100 mm的长方体。岩石网格采用六面体八节点的线性缩减积分单元C3D8R，并对PDC切削齿、冲击齿与岩石接触区域的网格进行细化[19]。对岩石下端施加固定边界条件，PDC切削齿和冲击齿定义为离散刚体，将其分别约束在一个参考点上，给切削齿参考点在切削方向赋予速度值：V=444 mm/s，给冲击齿参考点一个方向赋予位移值：26.3 mm，其中冲击齿距岩石面20 mm，冲击齿吃入岩石深度为6.3 mm，该冲击深度是根据冲击速度1 m/s时冲击试验所测冲击坑深度而设定的。冲击齿位移随时间的变化与单齿冲击试验设定为一致，其余方向进行位移和转动约束。

图3 切削齿、冲击齿与岩石几何模型Fig.3 Cutting teeth,impact teeth and rock models

数值模拟过程中，采用两个载荷步：第一个载荷步使冲击齿以26.3 mm的冲击位移冲击岩石，计算完成后获得冲击后应力分布和冲击坑体积；第二个载荷步采用切削齿以444 mm/s切削含冲击坑岩样，计算完成后提取结果。

为探究冲击齿冲击位置、冲击速度等冲击参数以及切削速度等切削参数对复合破岩效率的影响规律，通过正交试验对复合破岩数值计算进行参数敏感性分析，分析各因素对复合破岩的影响规律。表1为正交试验考虑的设计因素。

表1 正交试验的因素选择Tab.1 Factor selection of orthogonal experiment

2.2 模型验证

为了保证仿真结果的可靠性，需要对模型进行验证。本文从冲击坑形貌的角度进行模型本构验证。所建立的冲击试验模型如图4所示，输入条件为冲击速度为1 m/s时单齿冲击试验所记录的实际冲击位移。所用花岗岩的物理参数平均测量分别为：抗压强度为77.24 MPa，抗拉强度为4.56 MPa，弹性模量为6 GPa，泊松比为0.2。

图4 冲击试验仿真模型Fig.4 Impact test simulation model

单齿冲击破碎岩石试验原理为自由落体冲击，通过计算冲击高度来实现试验设定的冲击速度。此处冲击速度设定为1 m/s，冲击角度为90°，冲击齿自由落体并冲击岩石形成冲击坑后，测量冲击坑深度和直径。

通过对比冲击齿冲击岩石后形成冲击坑的形貌，如图5、图6所示，测量单齿冲击试验的冲击坑尺寸，冲击坑深度为6.3 mm，直径为12.8 mm。在对应仿真分析中，冲击坑深度为7.2 mm，直径为11.6 mm。通过仿真结果与试验结果相对比，冲击坑的直径相差9.3%，冲击坑深度相差14.2%，证明该数值仿真模型准确且可靠。

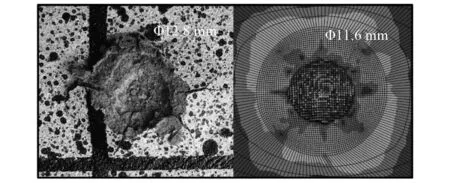
图5 冲击试验与仿真模型冲击坑形貌对比Fig.5 Comparison of impact pit appearance between impact experiment and simulation model

图6 冲击仿真冲击坑截面形貌展示Fig.6 Cross-sectional shape display of impact pit in impact simulation

2.3 网格无关性分析

为探究仿真模拟的网格无关性，并获得仿真分析最优网格划分尺寸大小，对PDC切削破岩仿真模拟进行了网格无关性的分析。考虑到切削齿的直径(15.875 mm)以及切削深度(2 mm)，故选择的网格大小分别为1.0 mm，1.2 mm，1.5 mm以及1.8 mm。如图7所示为四组单齿切削破岩仿真模拟切削齿所受平均切削力对比。

网格大小从1.0 mm增加到1.5 mm，平均切削力变化了0.19%，而网格大小从1.5 mm增加到1.8 mm时，平均切削力增加了8.4%。根据结果，对于网格尺寸范围在1.0～1.5 mm时，其计算结果的变化小于1%，且计算时间在可接受范围，因此下列模型采用1.2 mm网格大小。

3 复合破岩机理的试验及数值分析

为深入剖析复合钻头破岩机理，采用试验和数值模拟结合的方法，对分离式冲击-刮切过程中应力场、切削力变化和组合破岩过程进行分析。

3.1 岩石冲击后冲击坑形貌及应力场分布

单齿冲击后的岩石Mises应力如图8所示，冲击齿在岩石表面形成冲击坑，冲击坑周围区域的岩石没有发生破碎，但是冲击产生的应力波会对其造成损伤。为了准确地分析冲击坑周围岩石状态，在冲击坑附近选取一系列岩石单元节点，如图8所示，对这些节点上的压应力进行分析。

图8 冲击坑周围岩石单元节点选取示意图Fig.8 Schematic diagram of rock element node selection around impact pit

如图9所示，随着偏离冲击坑距离的增加，单元节点上所受等效压应力沿径向方向先增加后减小，在距离冲击坑7 mm左右，岩石单元压应力达到最大值，然后迅速下降；在距离超过10 mm后，出现波动，但整体仍然保持下降趋势；在20 mm处下降到最低点。由此得出，在偏移冲击坑距离为7 mm左右处的岩石所受破坏最严重，岩石强度最低，切削齿在此处切削时所受切削力最小；在偏移距离为20 mm左右的岩石强度则相对较高，对提高后续切削破岩贡献较小。

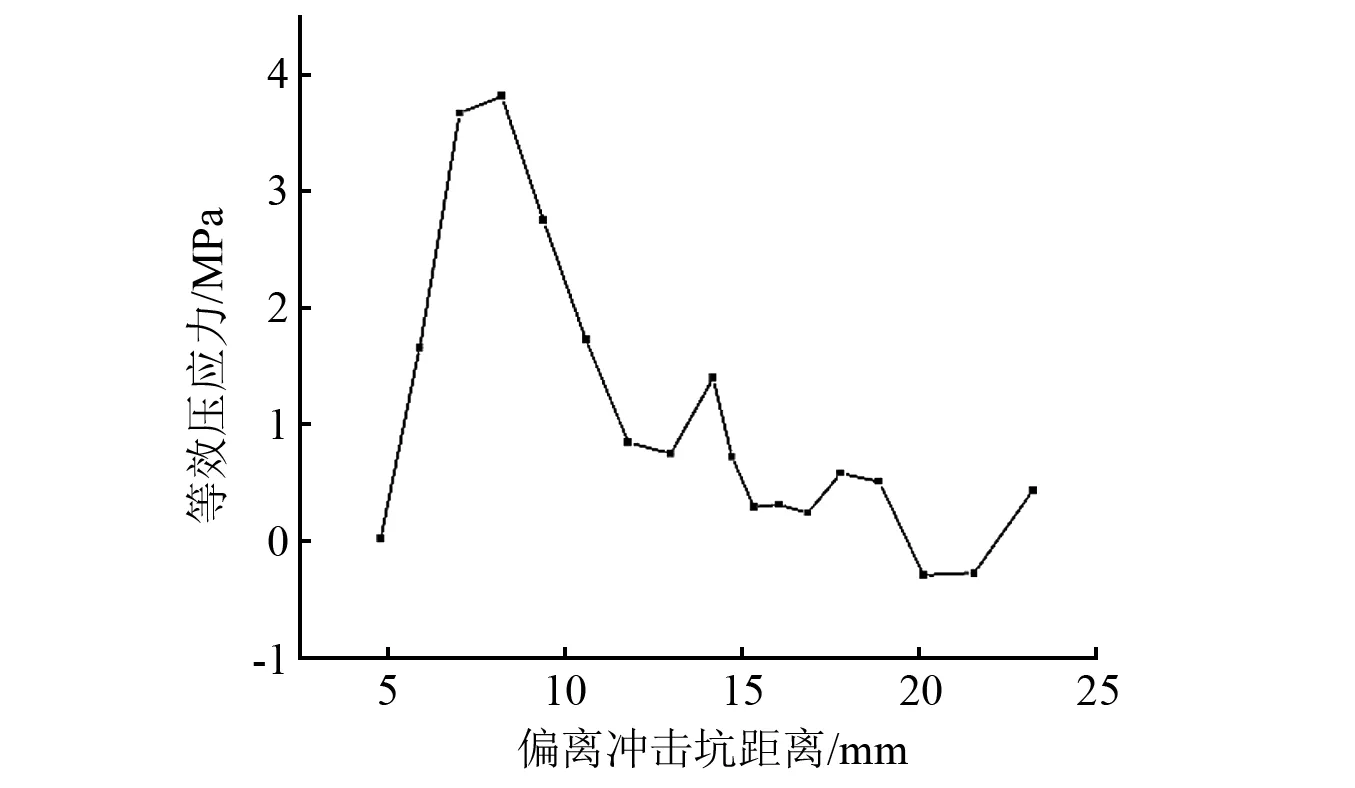
图9 冲击坑周围岩石不同单元节点等效压应力对比Fig.9 Comparison of equivalent compressive stress of different element nodes of rock around impact crater

观察单齿冲击试验中，不同类型冲击齿冲击所产生的冲击坑形貌，如图10所示，发现锥型齿的冲击效果最好，楔形齿次之，球面锥型齿的冲击效果最差。这主要是因为锥型齿的吃入效果最好，产生较大的冲击影响区域，这种影响对后续单齿切削较为有利。

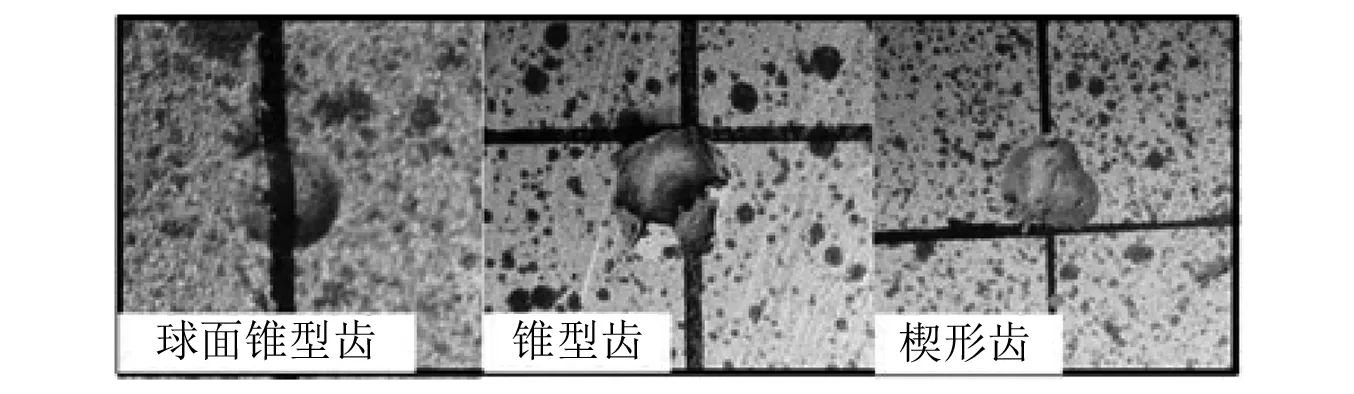
图10 不同冲击齿产生冲击坑形貌对比Fig.10 Comparison of the morphology of impact pits produced by different impact teeth

3.2 冲击坑对岩石切削过程的影响分析

上述冲击形成冲击坑后，采用切削齿对含冲击坑岩样进行切削试验。

3.2.1 冲击坑对岩石切削Mises应力场的影响分析

仿真模拟单齿切削含冲击坑岩样，对切削齿施加单方向切削速度。结果如图11所示，观察切削齿切削冲击坑时冲击坑附近岩石Mises应力变化。当PDC切削齿开始切削冲击坑时，冲击坑底部和与切削齿接触处岩石应力较大，随着切削齿继续切削，应力较高的区域逐渐变多，最终连通。该应力较高连通区域即为岩屑剥离过程中的裂纹产生路径，相比无冲击坑工况，该工况下岩屑破碎体积较大，破碎所需切削力也较小。因此，从应力分布变化和岩屑剥离角度来看，冲击坑对单元齿切削破岩体积提高和切削力改善具有显著增益效果。

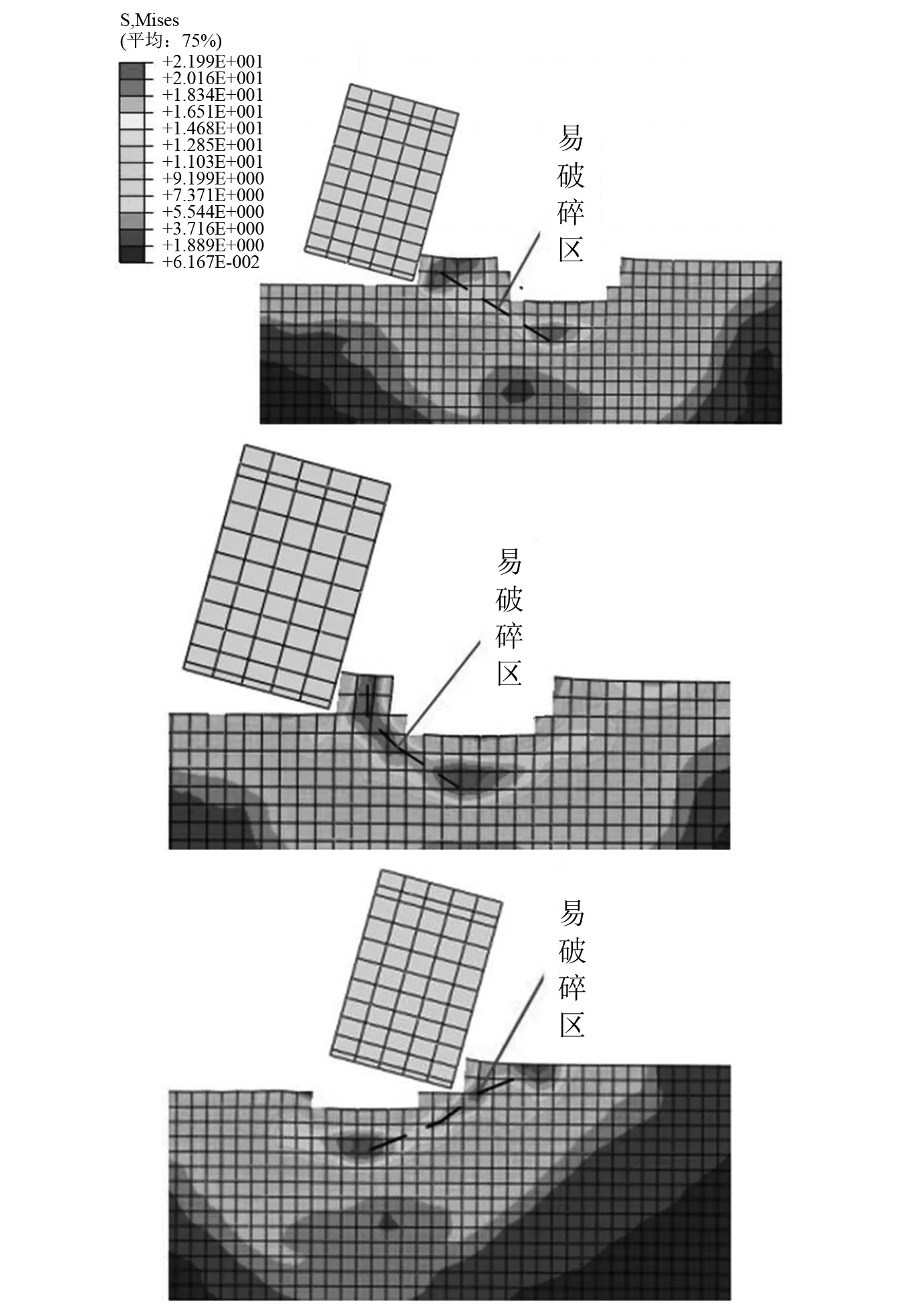
图11 切削齿切削冲击坑时岩石Mises应力分布Fig.11 Mises stress distribution of rock when cutting teeth cut impact pit

3.2.2 冲击坑对切削齿切削力的影响分析

采用试验和数值模拟分析冲击坑与切削路径间距的影响。通过分析复合切削破岩试验采集得到的切削齿切削冲击坑区域平均切削力结果。如图12所示，随着切削齿偏移冲击坑距离从0增加到20 mm，切削齿所受切削力逐渐增加。结合图11可知，当冲击齿冲击破碎使得冲击坑附近岩石强度降低，有利于降低切削齿切削所受切削力。

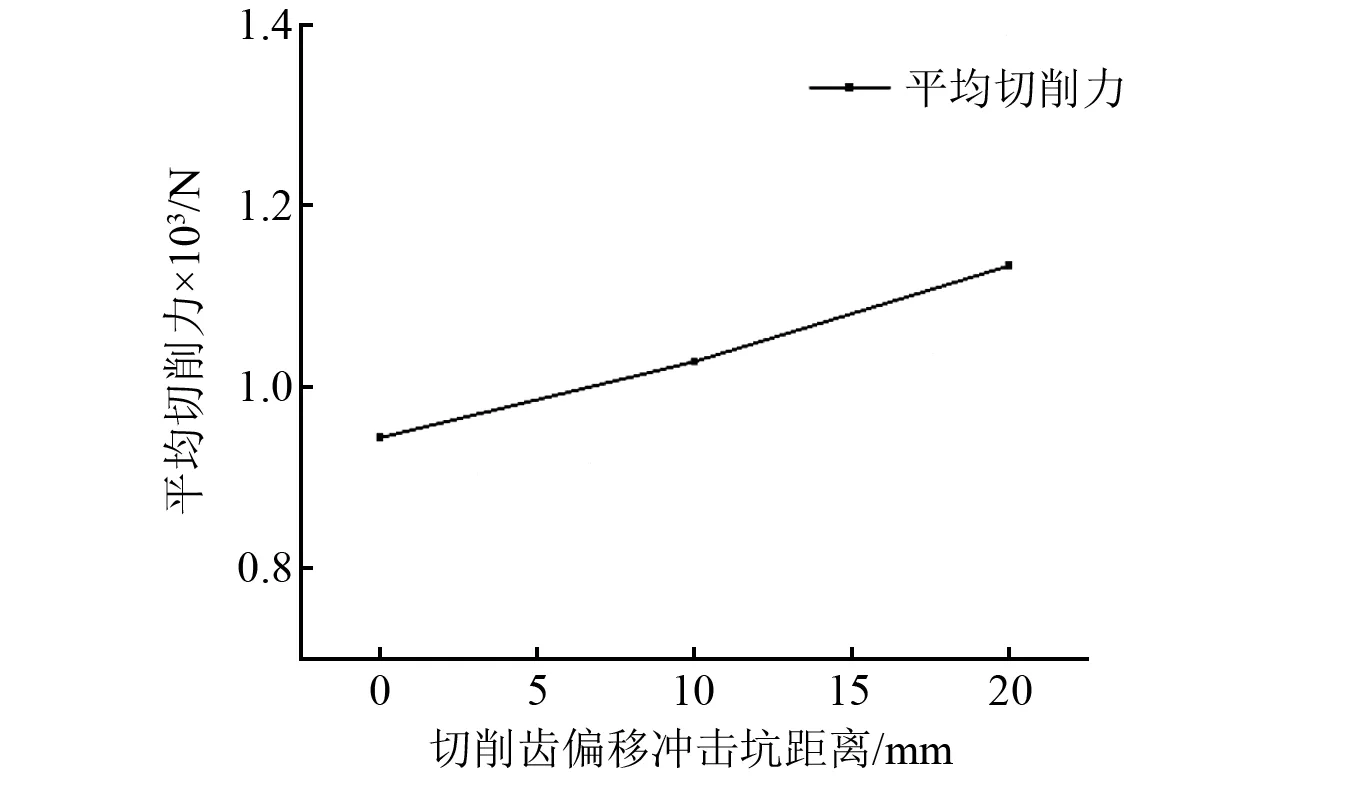
图12 偏移距离对平均切削力的影响Fig.12 Influence of offset distance on average cutting force

通过对比常规切削和复合切削破岩后的岩石表面最大主应力云图和形貌，如图13所示，常规切削破岩岩石表面整体拉应力值偏小，而复合切削破岩岩石整体的拉应力值较大，且拉应力值整体偏高。由于岩石的抗拉强度远远小于抗压强度，因此以拉应力破坏为主的复合切削更容易使岩石发生破坏，切削齿的破岩效率更高。对比两者形貌可以看出，有冲击坑时其切削路径在经过冲击坑时可形成联合破碎带。

图13 常规切削和复合切削对比Fig.13 Comparison of conventional cutting and compound cutting

3.3 常规切削和复合切削对比

为了进一步对比常规切削与复合切削过程中冲击坑周围岩石所受应力变化，在岩石截面上选取5个不同位置的单元，如图14所示。通过对比常规切削与复合切削过程中这5个位置的最大主应力变化趋势来分析冲击齿冲击岩石形成冲击坑对切削齿切削过程中的切削力的影响。

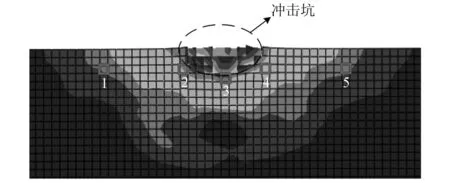
图14 切削路径上选取的5个不同位置单元示意图Fig.14 Schematic diagram of 5 different position units selected on the cutting path

如图15所示为单元1、单元2、单元3所受最大主应力变化趋势，单元4、单元5的最大主应力变化趋势分别与单元2、单元1相似，故图15仅列出1、2和3点应力变化。由于冲击载荷对岩石的影响[20-21]，在复合切削过程中，5个单元点所受应力变化更加平稳，可推断切削齿所受切削力变化也更加平稳。同时在切削过程中，常规切削时各单元所受应力均高于复合切削，故复合切削过程中，切削齿所受切削力更小。由此可见，冲击坑的存在不仅能够提高切削坑破碎体积，降低切削齿所需切削力，同时还能使得冲击坑附近待切削岩石单元应力受到明显的影响；冲击载荷对岩石进行冲击，将对岩石单元形成初步的压缩破坏，降低冲击区域岩石的强度，有利于降低切削齿所受切削力，提高切削齿的寿命。

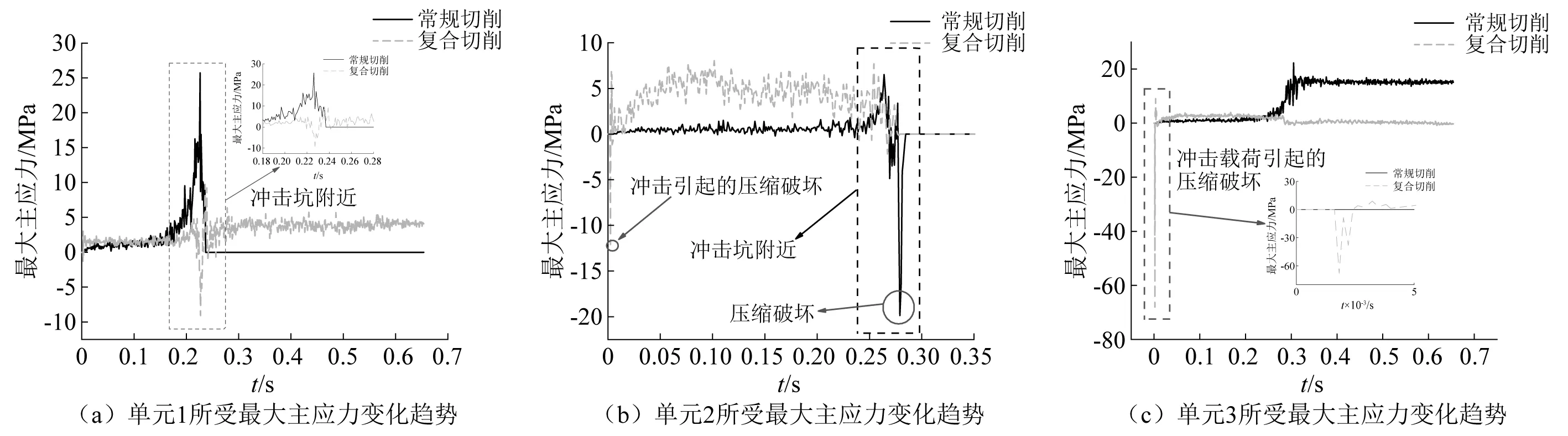
图15 不同位置单元节点最大主应力随时间的变化趋势Fig.15 Variation trend of the maximum principal stress experienced by elements at different locations

4 参数敏感性分析及全钻头钻进分析

4.1 破岩工艺参数敏感性分析

通过计算在不同冲击参数和切削参数下复合破岩的破岩比功，探究各因素对复合破岩破岩效率的影响规律。其中破岩比功(mechanical specific energy，MSE)表达式为

(3)

式中:M为切削齿切削过程所做的功,J；V为切削齿切削破岩的破碎体积，m3。

根据正交试验组进行数值模拟，得出破岩比功的极差结果，如表2所示，从正交计算结果的极差可以看出，影响较大的因素分别是冲击位置、切削速度、冲击齿类型以及切削深度。为了深入探究冲击工艺参数和切削工艺参数对破岩比功的影响，分别得到其影响规律如图 16～图22所示。

表2 破岩比功的极差分析Tab.2 Range analysis of MSE

4.1.1 冲击参数

如图16所示，随着冲击角度由30°增加到45°，破岩比功随之增加并达到最大值33.5×107J/m3，而后迅速下降，当冲击角度超过60°，破岩比功又继续增大。破岩比功随冲击角度的增加呈现波动变化趋势，可见本文工况下对单齿冲击存在最优冲击角度60°～75°。

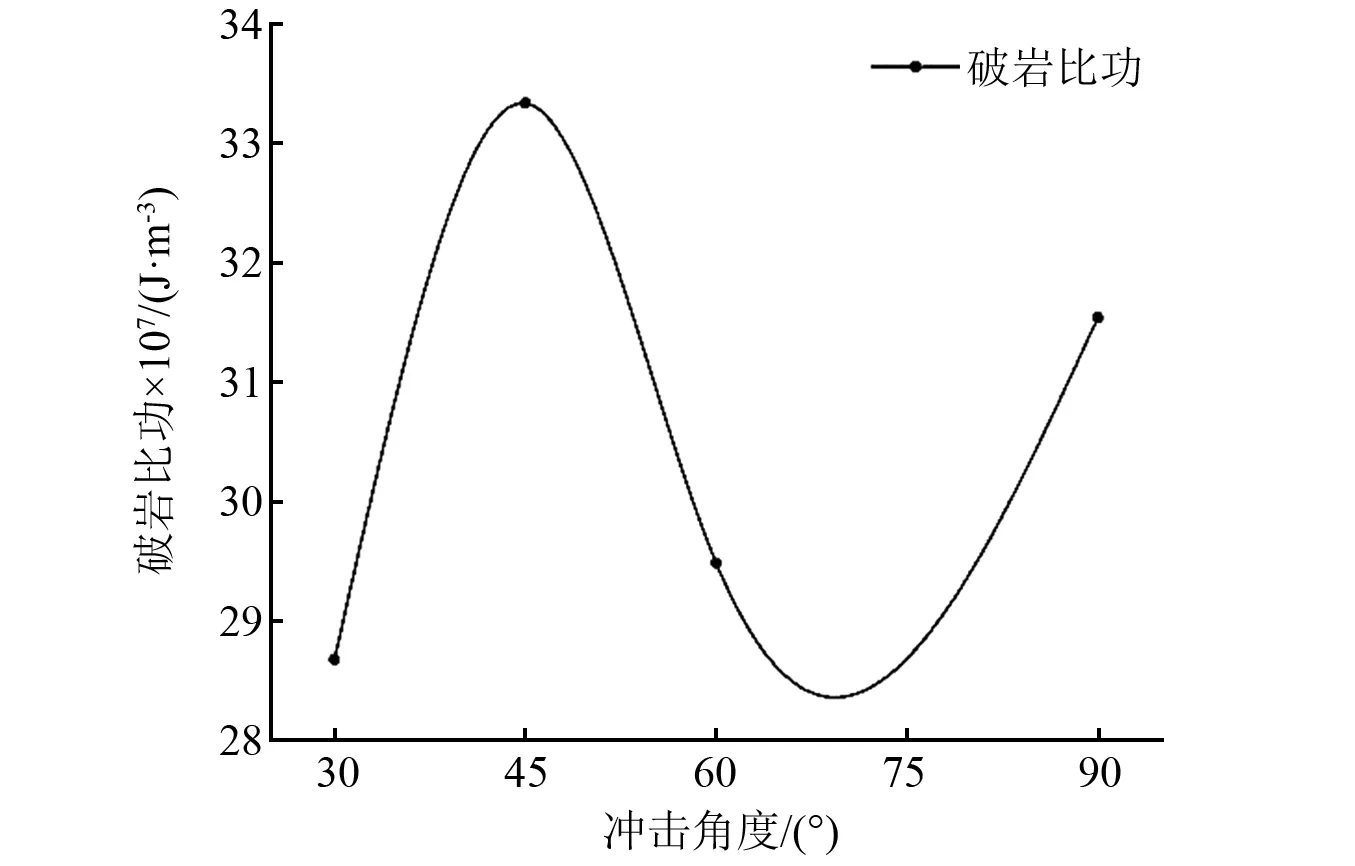
图16 破岩比功随冲击角度变化的变化趋势Fig.16 The changing trend of rock breaking specific work with impact angle

如图17所示，随着冲击速度的增加，切削破岩的破岩比功逐渐增加，尤其是当冲击速度超过7 m/s后，破岩比功增加更为迅速，不利于切削齿对岩石的破碎。这一规律表明一味增大冲击速度并不会提高复合破岩的破岩效率。

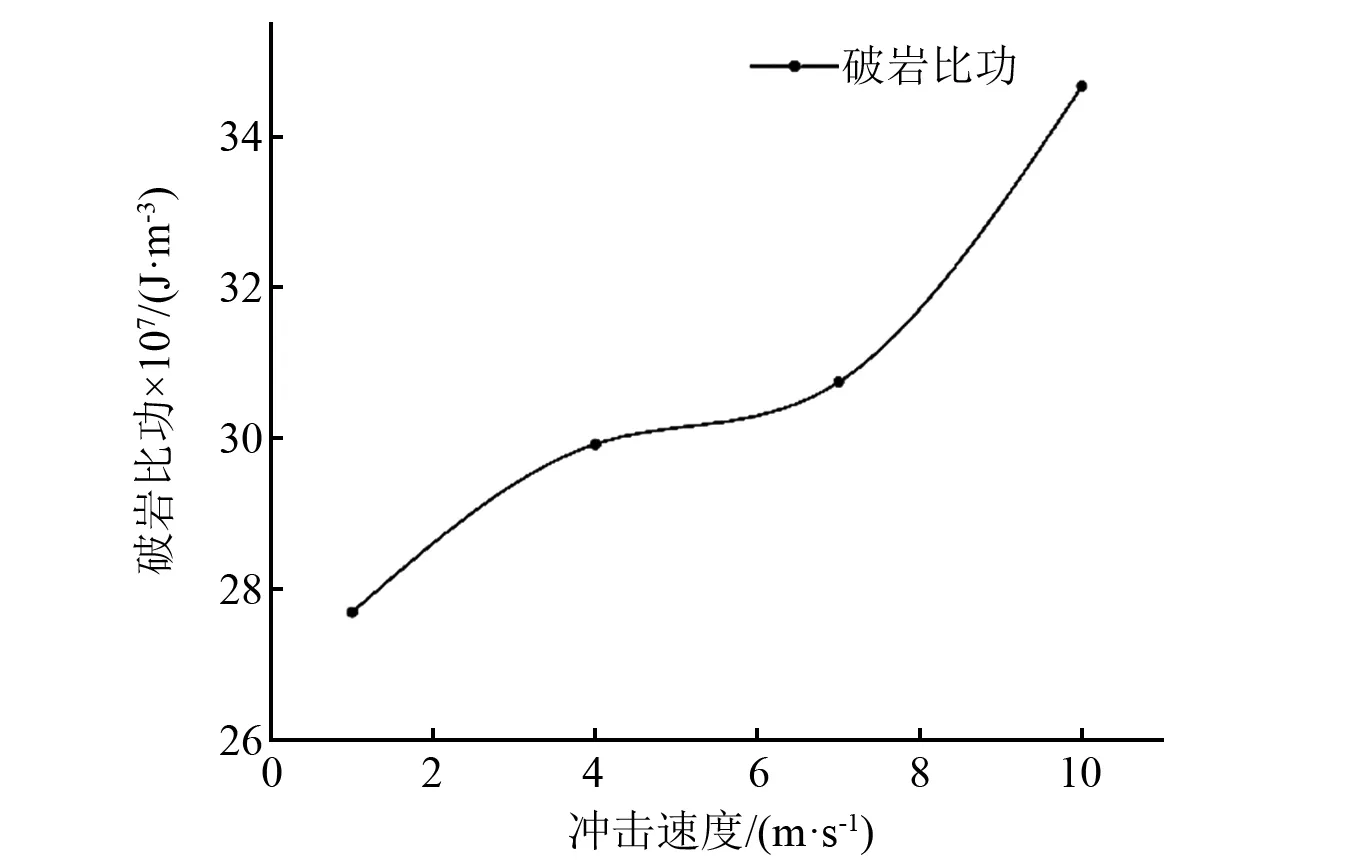
图17 破岩比功随冲击速度变化的变化趋势Fig.17 The changing trend of rock breaking specific work with impact velocity

如图18所示，对比四种不同类型的冲击齿的破碎比功可以发现，破碎比功最小为球形齿CQ1415，即四种齿在同样冲击速度下该球形齿的冲击破岩比功最佳。结合单齿冲击试验各类型冲击齿产生冲击坑形貌，发现球形齿虽然吃入岩石不够深，但却较大影响岩石的强度，提高切削齿的切削破岩效率。

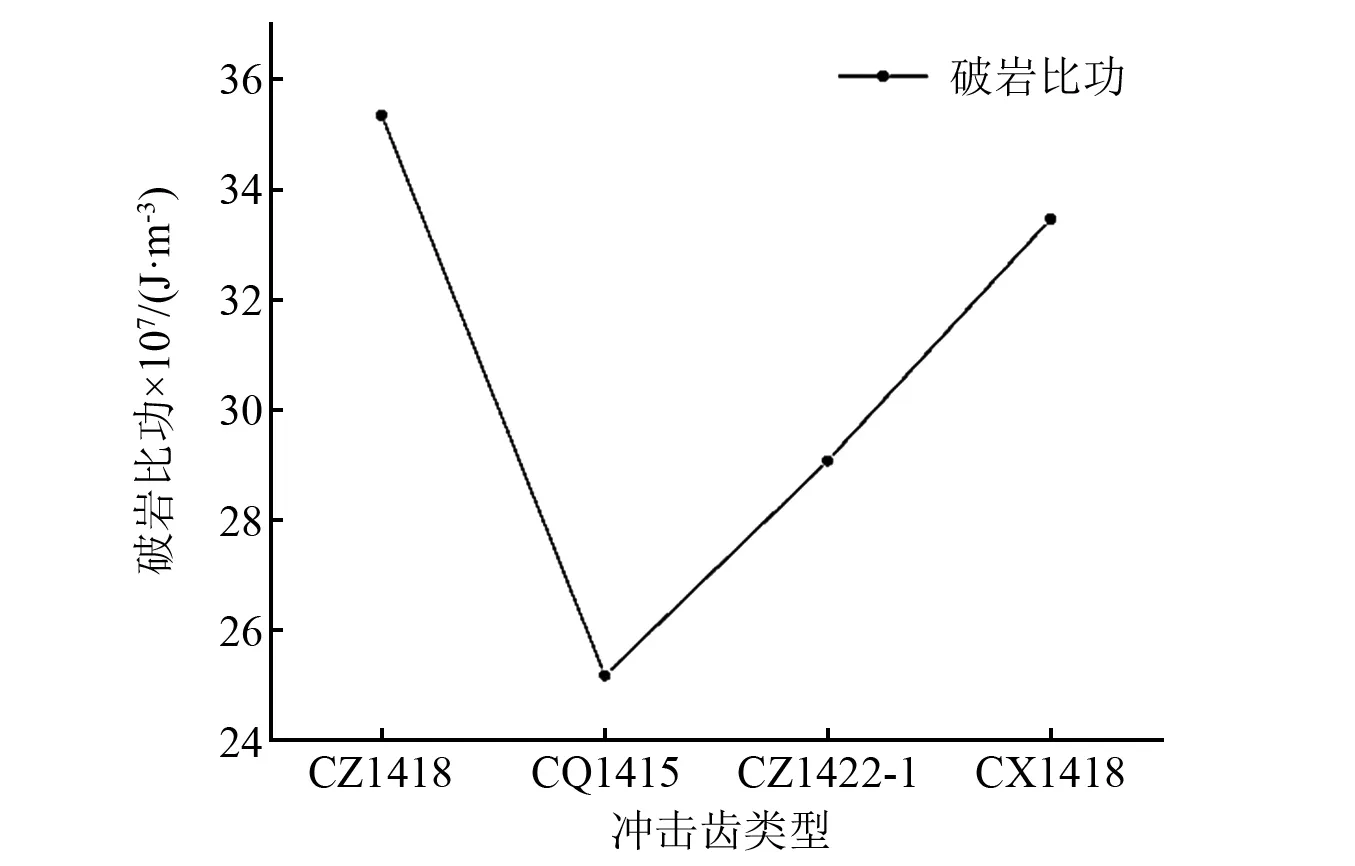
图18 破岩比功随冲击齿类型变化的变化趋势Fig.18 The changing trend of rock breaking specific energy with the change of impact tooth type

4.1.2 切削参数

切削齿切削路径偏移冲击坑距离是分析冲击齿与切削齿组合破岩效果的重要指标参数，是设计复合钻头布齿的关键。如图19所示，当偏离切削轨迹距离不断增大，破岩比功由291.5 J/cm3增加到339.5 J/cm3，破碎比功略微上升，随着偏离距离由20 mm增大至60 mm，破碎比功出现大幅下降。在单齿切削试验中，随着偏离切削轨迹距离不断增大，平均切削力不断增大。表明切削路径与冲击坑位置偏离一定距离，虽然会部分提高切削齿切削力，但复合破岩的破岩比功呈现大幅下降趋势，有助于提高复合切削效率。

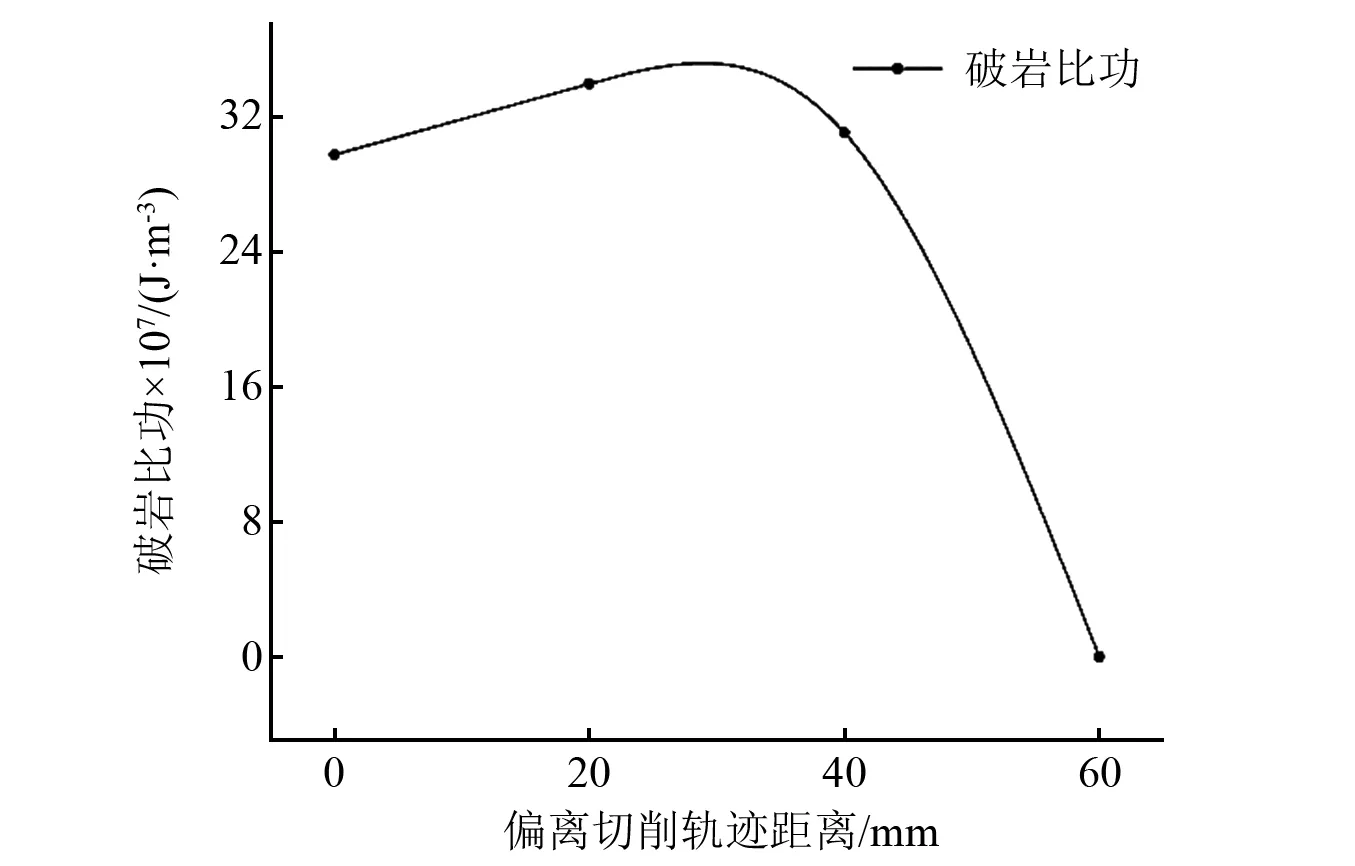
图19 破岩比功随冲击位置变化的变化趋势Fig.19 The changing trend of rock breaking specific work with impact position

如图20所示，随着切削速度从1 m/s增加到20 m/s，破岩比功由20.7 J/cm3增加到694.7 J/cm3，呈现持续上升趋势，增长了约34倍，严重降低了复合破岩的破岩效率。由于切削速度对破岩比功的影响较大，故设计该分离式复合钻头时应考虑较小的切削速度。

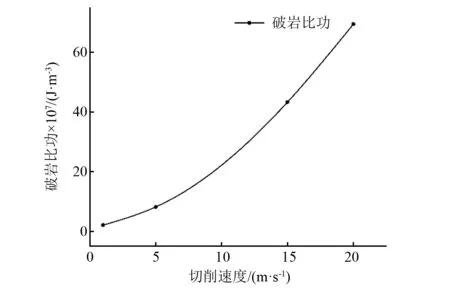
图20 破岩比功随切削速度变化的变化趋势Fig.20 The changing trend of rock breaking specific work with cutting speed

如图21所示，随着切削深度的增加，单齿切削的破岩比功持续上升，特别是切削深度从3 mm增加到4 mm时，破岩效果下降的尤为剧烈。这一规律表明较小的切削深度将更有利于提高复合破岩的破岩效率。

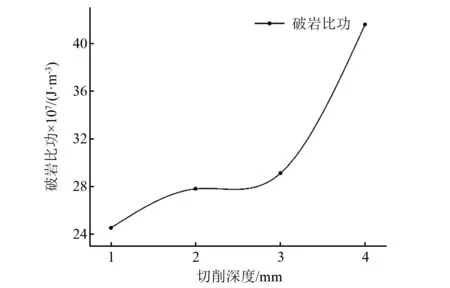
图21 破岩比功随切削深度变化的变化趋势Fig.21 The changing trend of rock breaking specific work with cutting depth

如图22所示，切削倾角由10°增加到20°，破岩比功随之增加，当切削倾角为20°时，切削齿的破岩比功达到最大值；切削倾角继续增大，破岩比功随之减少。由于没有进行更多的切削倾角下的计算，无法判断最优的切削倾角。

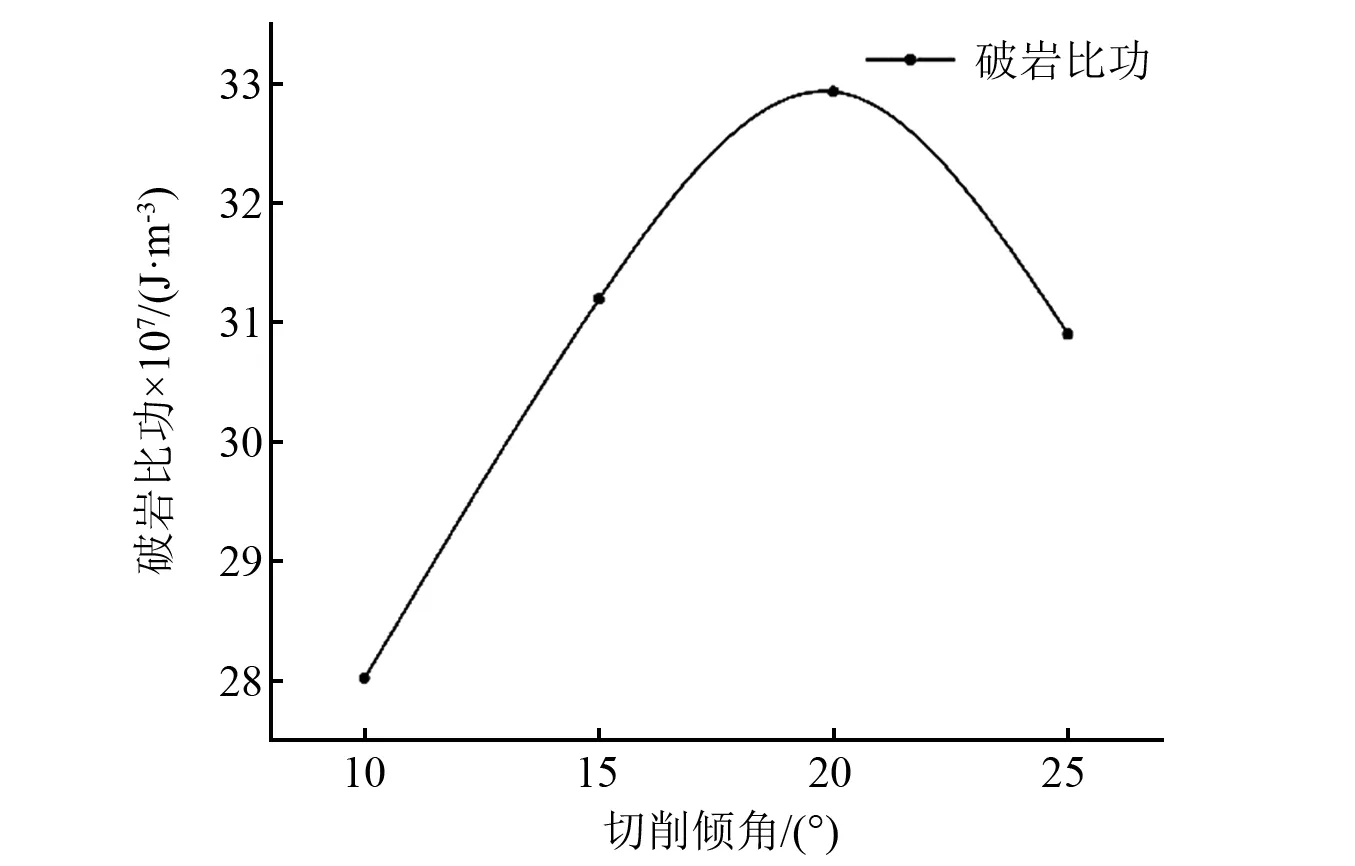
图22 破岩比功随切削倾角变化的变化趋势Fig.22 The changing trend of rock breaking specific work with cutting inclination angle

4.2 全尺寸钻头钻进对比分析

为了比较冲击-刮切复合钻头与常规PDC钻头在钻进时的差异，参考实际钻井设计了全尺寸钻头的钻进仿真模拟，将PDC钻头简化，只保留冲击齿以及切削齿，如图23所示。对于复合切削，先对8 mm直径的冲击齿施加6.3 mm冲击位移，再对PDC齿施加钻压和转速旋转切削岩石；对于常规切削，仅对切削齿施加钻压和转速；为对比分离式冲击-刮切复合钻头钻进破岩，将本文复合钻头固定刀翼与冲击齿固定在一起进行同步周期性冲击和切削，以模拟冲击器对钻头施加周期性旋冲，在数值模型中对整体切削齿和冲击齿施加周期性的冲击位移以及钻压和转速。全尺寸钻头钻进井底的形貌及其应力对比如图24所示。

图23 全尺寸钻头简化模型Fig.23 Simplified model of full-size drill

图24 全尺寸钻头钻进井底形貌及应力对比Fig.24 Bottom morphology and stress comparison of full-size drill bit

比较不同钻头破岩后的岩石破碎区形貌，如图25所示，复合钻头切削破岩时，冲击齿冲击岩石形成明显的冲击坑，有利于PDC齿切削破岩。因此冲击载荷的存在会大大降低岩石的破碎难度，进而提高后续切削的破岩体积和破岩效果。

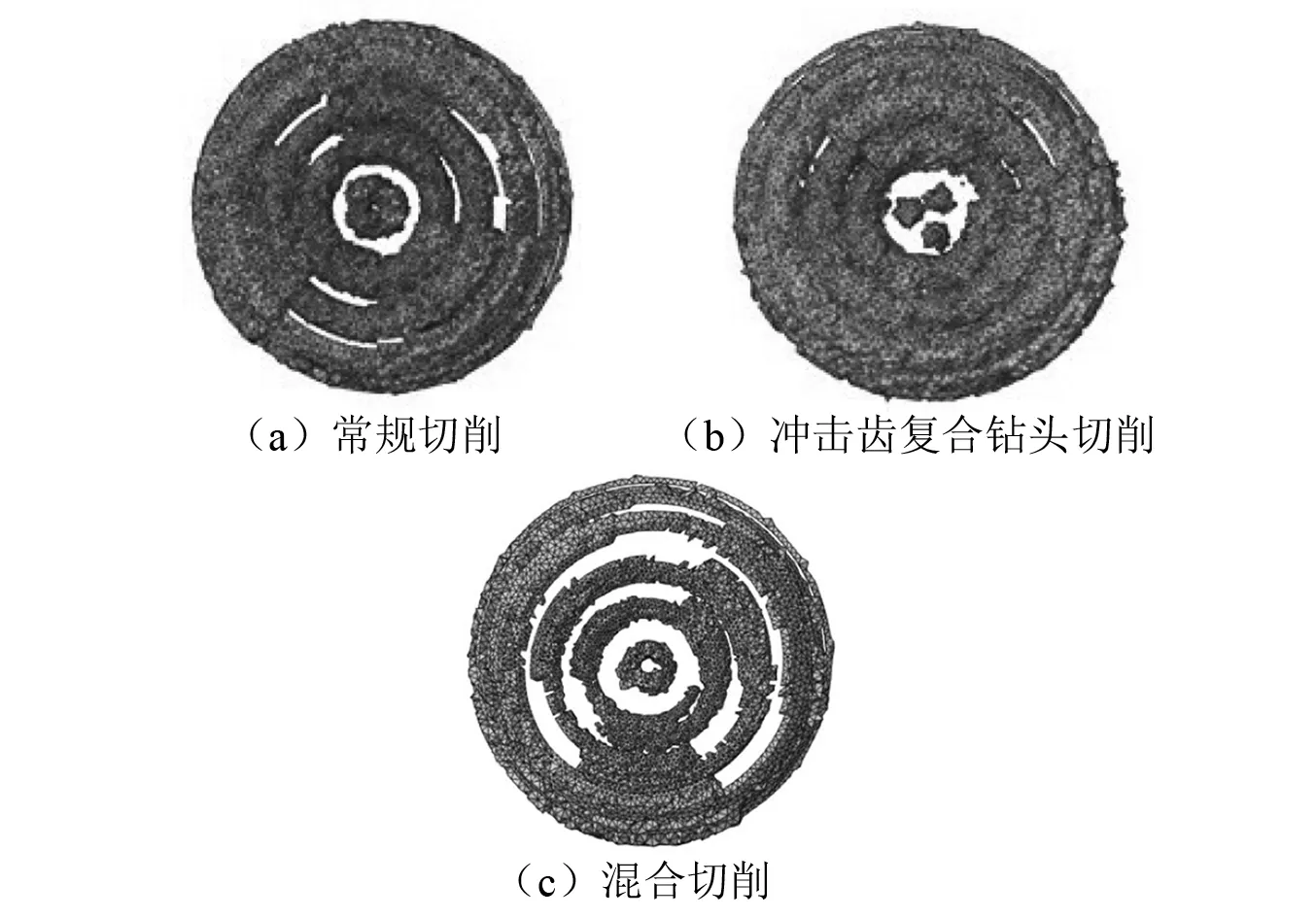
图25 各钻头钻进仿真被破碎岩石单元的形貌对比Fig.25 Comparison of the morphology of the broken rock unit of each drill bit in the simulation

如图26所示，通过对比三种类型钻头被破碎的岩石质量与钻速，与常规PDC钻头相比，复合钻头的破岩体积增加了约37%，机械钻速增加了约13%；与混合切削PDC钻头相比，破岩体积增加了约137%，机械钻速增加了约93%。对比分离式复合钻头的钻进破岩和混合式钻进破岩，可以发现混合式钻进破岩下切削齿切深周期性变化(见图26(b))、冲击齿周期性冲击井底，使得混合式复合钻头钻进破碎体积偏小。由此可见，分离式冲击-刮切复合钻头更能降低钻进的时间，节约钻井成本。

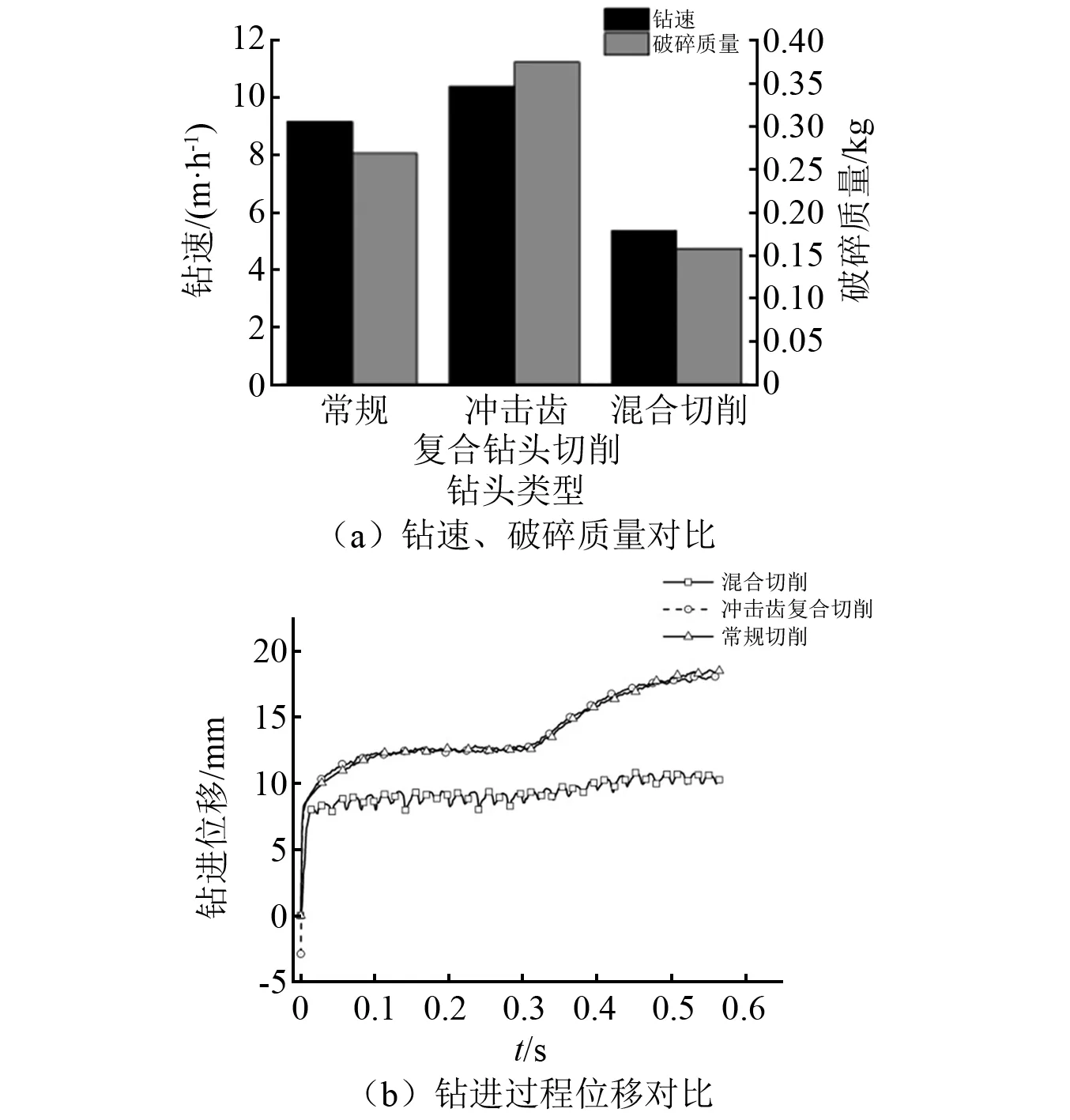
图26 不同钻头钻速、钻进位移和破碎质量对比Fig.26 Comparison of drilling speed and crushing quality and drilling displacemen of different bits

5 结 论

通过单齿冲击、单齿切削和全尺寸钻头复合破岩的数值模拟和试验，分析了冲击齿冲击对岩石形貌和应力的影响，以及冲击坑对切削过程中切削齿切削力的影响。并研究了各冲击参数和切削参数对该钻头复合破岩效率的影响规律，结论如下：

(1)冲击-刮切复合破岩中，冲击齿冲击岩石形成冲击坑，对岩石进行初步的压缩破坏，并降低冲击区域岩石的强度。相比于常规破岩，PDC切削齿所受切削载荷更小，切削力变化更加平稳。

(2)冲击速度、切削速度和切削深度越大，破岩比功随之增大，不利于提高复合破岩效率；切削路径偏离冲击坑超过20 mm后将显著提升复合破岩效率；所选冲击齿类型中，球形冲击齿能较好的冲击岩石并降低岩石强度，利于后续切削齿切削。

(3)在冲击-刮切复合钻头设计中，根据岩石特性、切削齿直径和冲击齿直径，选择球形冲击齿、1 m/s的冲击速度、1 m/s的切削速度、1 mm的切削深度和60 mm的切削路径偏离冲击坑位置，所优选的分离式冲击-刮切复合钻头更能降低钻进的时间，节约钻井成本。

致 谢

该分离式冲击-切削复合钻头由钻头研究所杨迎新等人首次提出，并经杨迎新、蔡灿、陈炼、任海涛和谢松等人逐步完善设计和研制，特此致谢说明。