非一致地震激励的改进位移输入法：误差分析与应用

李 宁，陈 浩，李忠献

(1.天津大学 建筑工程学院 滨海土木工程结构与安全教育部重点实验室，天津 300350；2.天津大学 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室，天津 300350)

如何正确计算空间差动地震动对大跨度结构的非一致效应及其影响规律，仍然是抗震研究的热点问题[1-3]。为了保证结构的安全，考虑到设计及应用的方便，需采用恰当的计算方法进行结构的非一致动力反应分析。通常的多点多维激励分析方法依据地震动模拟输入和等效输入荷载的方式不同，分为多个类型[4-10]。时域方法不仅适用于结构线性分析，也适用于非线性分析，是当前最具有普适性和有效性的计算方法。时域内多点激励计算方法主要有：直接求解法(direct solving method,DSM)、相对运动法(relative movement method,RMM)、位移输入法(displacement input method,DIM)、大质量法(large mass method,LMM)[11]和大刚度法(large stiffness method,LSM)。DIM法也是当前诸多有限元工具容易实现的一般方法，在多点激励计算中被广泛应用。而为了考虑零频信号或地面残余位移，DIM尤为适合。

DIM通过引入基底位移作为激励，求解结构响应，不同于加速度场引入惯性效应。近年来，有关学者针对DIM的计算精度、存在的问题以及解决方法等展开了研究。罗超等通过对DSM、DIM、RMM和LMM的对比研究指出，DIM方法的计算精度可以满足工程要求。惠迎新等以跨断层桥梁为研究对象，讨论了非一致激励下DIM和LMM的适用性以及误差产生的原因。结果表明：DIM能够更好考虑永久地面位移对结构响应的影响，而LMM则无法考虑，但这并不是LMM本身引起的，而是有限元实现方法不同所导致。柳国环等[12]指出，当空间结构底部单元为非经典阻尼时，DIM不会存在计算结果的不收敛问题。而国巍等[13]研究指出，DIM在隔震结构中盲目使用可能会导致严重的错误。Wilson等认为要使DIM与RMM达到相同的计算精度，则需要更小的激励步长和积分时间步长，而田玉基等却给出了相反的结论。杜宪亭等在上述研究的基础上指出：在积分方法和步长相同时，RMM较DIM易得到更好的精度，而在模态分析方法中则会得到相反的结论。李永华等[14]研究指出，RMM和DIM中由于阻尼假定的不同，会导致两个方法的计算结果存在巨大差异。在Rayleigh阻尼模型下，质量比例阻尼部分是导致误差的主要来源，并与阻尼比的大小、激励频率和结构基本频率的比值有关，而刚度比例阻尼部分不会产生误差；在单元阻尼下，两种方法计算结果基本一致。柳国环等也指出，DIM在考虑Rayleigh阻尼时的计算结果可能不稳定和不可靠，并提出了附加无质量束缚元和无质量刚性元的修正方法。笔者认为应将结构考虑为Rayleigh假定和非比例阻尼假定两类体系对待。

本文采用Rayleigh阻尼模型，在对多点激励分析理论以及现有方法分类探讨的基础上；研究了DIM的适用条件，讨论了其计算精度影响因素等，并基于理论分析提出和验证了适用于空间结构非一致激励分析方法：改进的IDIM方法(improved DIM)，该方法可推广用于大型结构非一致激励的动力响应计算。

1 DIM和MRE修正方法

1.1 DIM的理论分析

对于在地面上刚性连接的集中质量结构分析模型，其地震激励下增量动力平衡方程为

(1)

(2)

通常，采用集中质量进行建模，则Mts=0；于是式(2)可以化简为

(3)

(4)

式(4)即为DIM法求解地震差动结构反应的式子。

1.2 MRE修正方法

为了避免改动计算程序降低操作复杂性，MRE法的分析示意图如图1所示。

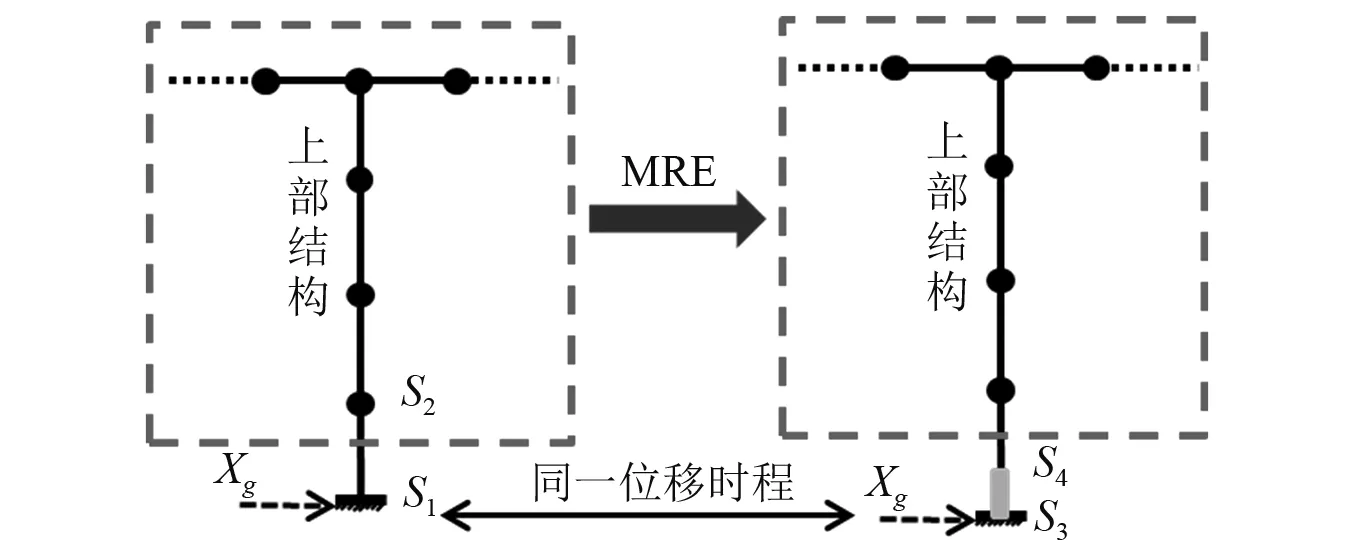
图1 MRE建模示意图Fig.1 Sketch of model adopted in MRE

在采用MRE进行建模时，可通过比较设置无质量刚性元前后结构的自振特性是否一致，判断刚性元的刚度是否足够。同时，应注意附加节点S处的质量为零。MRE修正后，由于DIM中忽略的阻尼力直接通过无质量刚性元显著影响该刚度单元的相对位移和内力，对原结构各质点的影响甚小，从而巧妙避免了DIM的误差问题。柳国环等采用商用软件，实例分析验证了MRE的合理性。然而，直观地可以看出，对刚度比例阻尼系数β较大的结构，底部刚性元尺度、相对刚性大小可能导致MRE方法并不具有通用性。下面将通过实例进行分析并指出具体原因，提出修正思路。

2 算例大跨结构模型及MRE的误差分析

2.1 算例模型及输入地震动

为验证MRE的效果，选取如图2所示的桥梁结构进行分析，该桥梁跨径为10 m+30 m+10 m，墩高6 m，材料弹性模量为2.1×1011N/m2，记为模型1。为验证MRE对于任意结构的适用性，改变弹性模量为1.0×1010N/m2，桥墩高度为10 m，其余参数不变，记为模型2。原模型与MRE模型的自振周期特性对比如表1所示(T1约为1.16 s和6.53 s)，可以看出，模型中的无质量刚性元未引起体系前几阶变化。

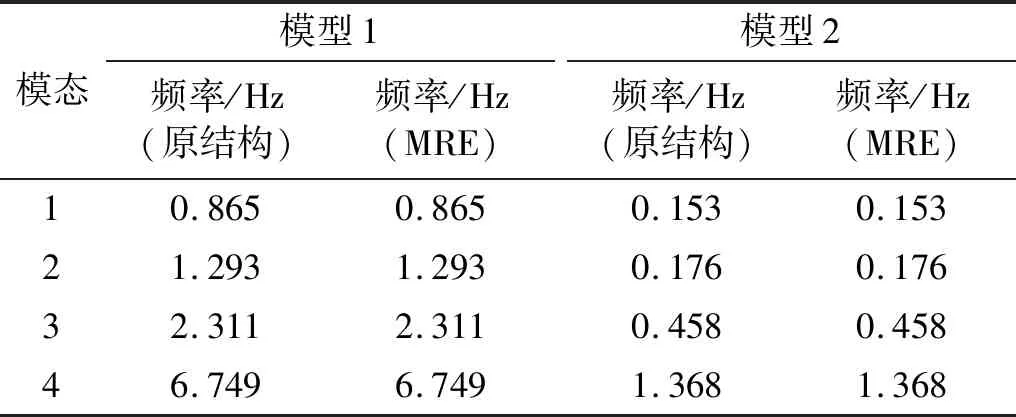
表1 桥梁结构模态信息Tab.1 The modal information of bridge structure

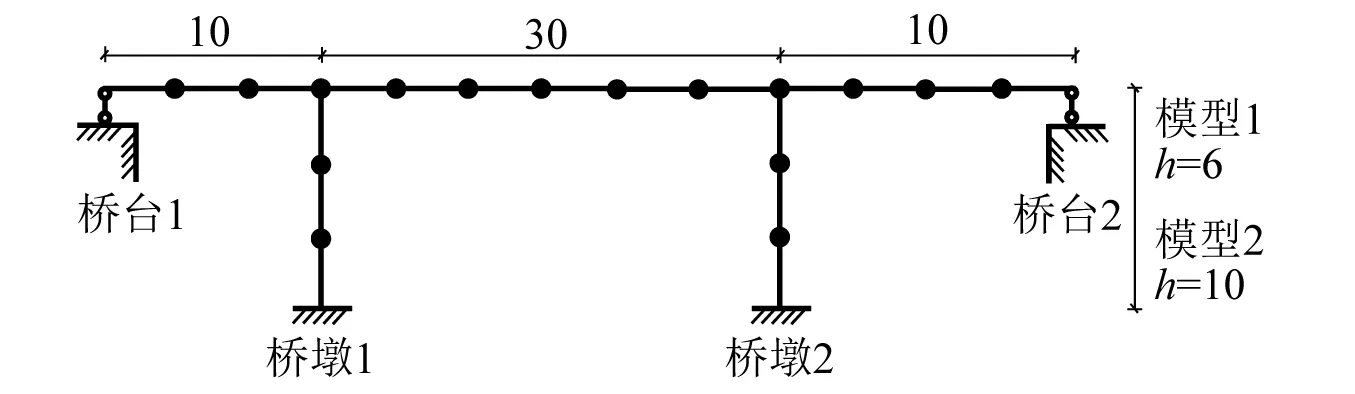
图2 桥梁结构有限元模型简图(m)Fig.2 Finite element model sketch plot of bridge structure (m)

2.2 MRE法的误差分析

因DSM可以视为理论上的精确解，因此本文定义计算误差η为

(5)

式中：f1(t)为DSM计算的结构响应；f2(t)为DIM或MRE的计算结果。

图3和图4分别给出了阻尼比为5%时，模型1和模型2采用DIM计算的桥墩1墩顶位移和墩底内力的响应峰值误差以及地震动速度增量峰值分布图。由计算结果可知，对于模型1，墩顶位移峰值误差的变化范围为0.01%～0.42%；墩底剪力变化范围为113.53%～406.78%。墩底弯矩为15.57%～77.04%；对于模型2，墩顶位移峰值误差的变化范围为0.01%～1.29%；墩底剪力误差的变化范围为130.79%～1 010.76%；墩底弯矩误差的变化范围为11.29%～390.47%。可以看出，DIM计算的墩底剪力和墩底弯矩相比于墩顶位移有着不可忽略的误差。

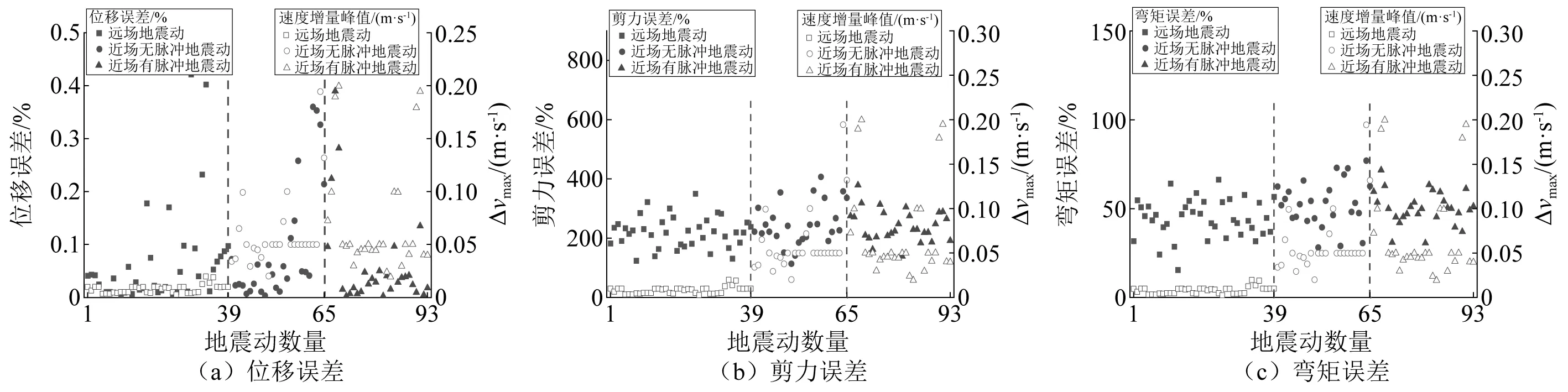
图3 模型1采用DIM计算反应误差分布Fig.3 Error distribution of model 1 with DIM

图4 模型2采用DIM计算反应误差分布Fig.4 Error distribution of model 2 with DIM

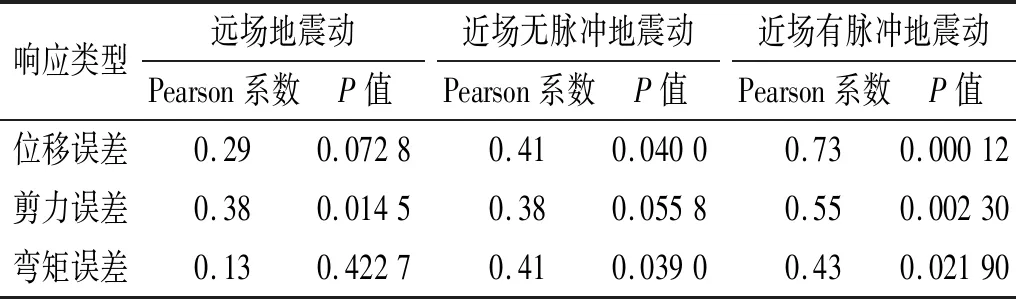
表2 模型1响应峰值误差与地震动速度增量峰值的相关性Tab.2 Correlation between the maximum response error of model 1 and the maximum incremental velocity of GMs

表3 模型2响应峰值误差与地震动速度增量峰值的相关性Tab.3 Correlation between the maximum response error of model 2 and the maximum incremental velocity of GMs

表4给出了2桥梁模型和采用MRE的峰值误差最大值。对于模型1，MRE法给出的桥墩1墩顶位移、墩底剪力和墩底弯矩的计算误差最大不超过0.41%，0.76%和1.19%；而对于模型2，MRE法给出的桥墩1墩顶位移、墩底剪力和墩底弯矩的计算误差最大达到了1.29%，27.21%和8.95%。上述计算结果表明：MRE法对相对短周期结构(模型1)具有良好的修正效果；但对于形如模型2的长周期结构，仍存在无法忽略的误差。需要说明的是，此处使用MRE的刚性元，仅考虑了不导致体系前5阶模态改变，尚未深入考虑模态截止阶数的影响。因此，MRE方法不具有通用性。

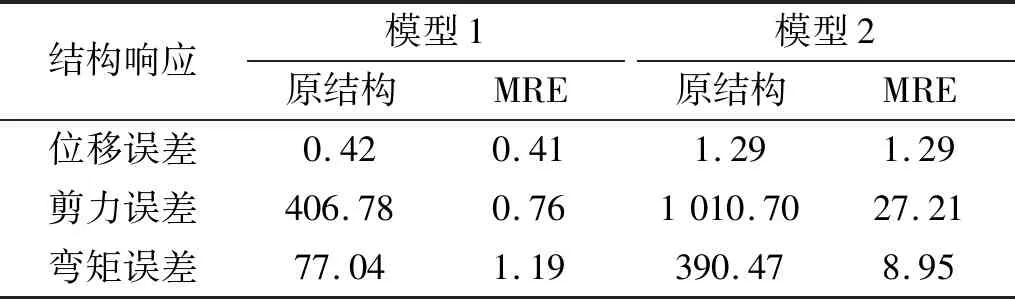
表4 不同模型的计算误差最大值Tab.4 The maximum analysis error of different models %

2.3 误差源和模拟方法的进一步探讨

为寻找MRE方法对于类似模型2所示结构计算的误差来源，本节进一步分析。对比模型1和模型2发现，两模型自振特性不同，进而导致刚度比例阻尼系数β大小不同。对于模型1，阻尼比为5%时，比例阻尼系数以前两阶模态进行计算，刚度比例阻尼系数仅为0.007 4，对于模型2，则为0.048 4。此时，刚度很大的无质量刚性元的牵连自由度也有较大的刚度比例阻尼反力产生，导致计算误差。理论上，当节点S1和节点S处的质量为零时，由结构动力学可知，有式(6)成立

(6)

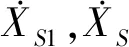
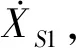
2.4 MRE法误差来源的数值验证

为验证上述探讨的正确性，图5给出了模型1和模型2在NGA953地震动(MUL279方向)作用下，结构阻尼比为10%时(为明确误差来源而设置)，无质量刚性元节点S和节点S1处的位移时程、速度时程以及桥墩底部的剪力时程。由图5可以看出：对于模型1，节点S1的位移时程和节点S处的位移时程相吻合；但对于模型2，节点S1处的位移时程并不等于节点S处的位移时程。也可以看出，对于模型1和模型2，节点S1处的速度时程为零，即动力时程只有位移场施加了，程序未考虑牵连速度。由于模型2的S处位移时程存在误差，导致其速度时程也会存在误差，最终使得剪力存在误差，如图5(c)所示。应当注意到，S1处的位移时程和速度时程为NGA953地震动的位移和速度时程。

图5 结构响应时程Fig.5 Structural response time histories

3 改进DIM方法的提出及数值验证

为避免前述所有模拟中可能的误差源，本节在MRE法的基础上，给出仅修正激励和同时修正模型和激励两种修正方法，便于软件实现和选用。

3.1 同时考虑模型及激励(I1-DIM)

上述分析指出，MRE方法修正后，DIM计算时，节点S处的位移和速度时程可能并不等于S1的位移、速度时程，即和原始地震动时程存在差异。本文根据式(6)，建议对输入的位移时程进行修正，如图6(a)所示，即

(7)

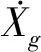
3.2 仅考虑动力激励(I2-DIM)

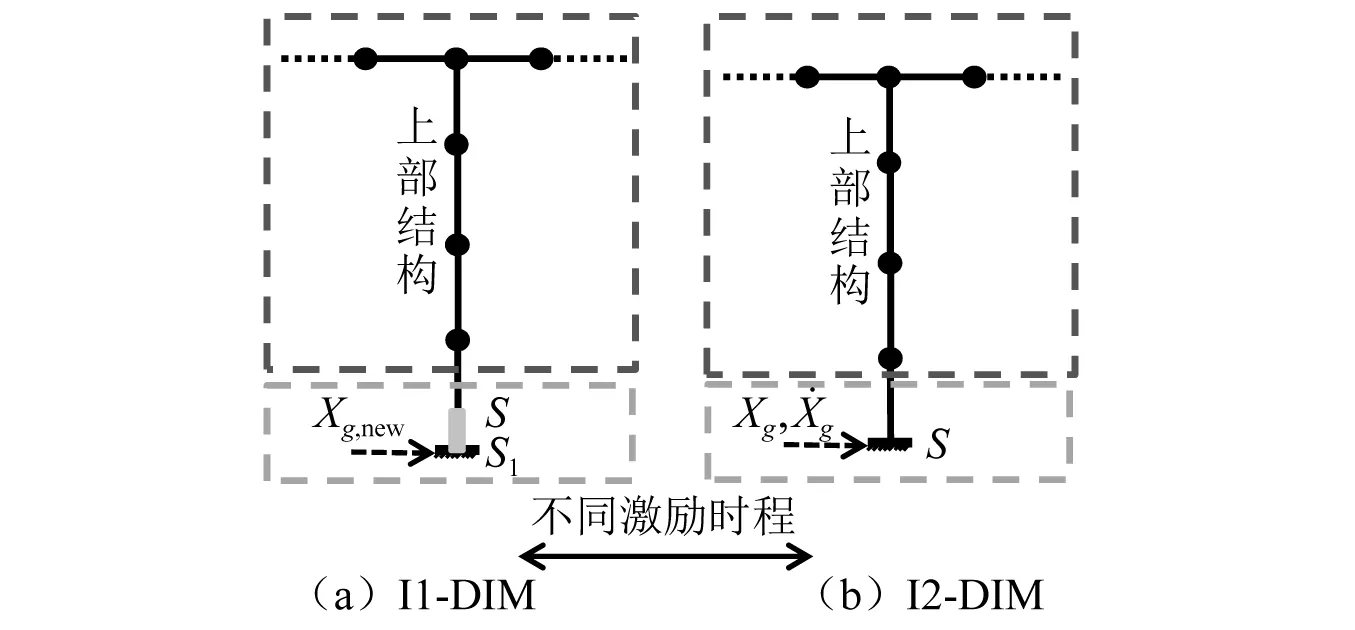
图6 改进的DIM方法Fig.6 Improved DIM methods

3.3 数值验证

本节仍采用前述模型2及地震动。图7给出了NGA953(MUL279)地震动激励下，结构阻尼比为20%时，采用二种修正后DIM计算的、无质量刚性元节点S和节点S1处的位移时程、速度时程以及桥墩底部的剪力时程。

图7 结构响应时程Fig.7 Structural response time histories

由图7可以看出：当采用I1-DIM修正后，尽管约束S1的位移时程不再等于原始地震动位移时程，且速度时程仍恒为零，但桥墩底部S处的位移时程和速度时程均等于原地震动，即，模型非一致激励输入是正确的。桥墩底部的剪力时程也和DSM的计算结果一致，验证了I1-DIM法的正确性。采用I2-DIM，桥墩底部S处的速度时程不再为零，其位移时程和速度时程也均等于原始地震动时程，且其修正后的墩底剪力也几乎完全等于DSM结果。即：采用I2-DIM后的计算结果也能达到计算精度的要求。表6给出了在不同阻尼比以及前述所有地震动激励下，采用I1-DIM和I2-DIM计算的桥墩1墩顶位移、墩底剪力和弯矩的峰值误差最大值，可以看出，最大误差不超过2.95%。至此，前述提出的两种修正方法，对于任意阻尼系数和任意地震动均具有适用性，且适用于非线性通用计算分析平台使用。

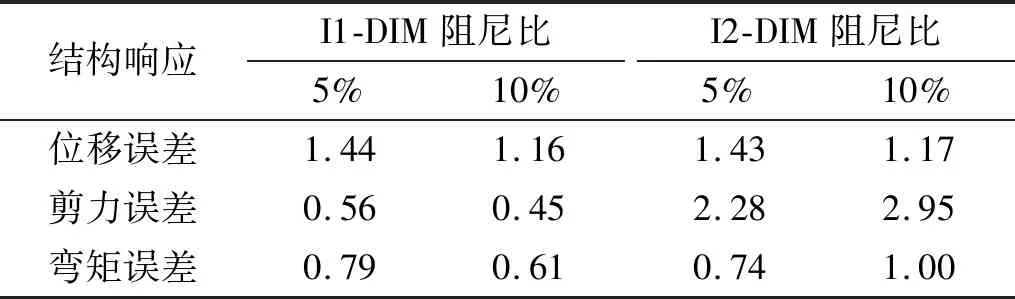
表6 I1-DIM和I2-DIM的计算误差最大值Tab.6 Maximum error using I1-DIM and I2-DIM %

I1-DIM方法和I2-DIM方法仍存在较小的计算误差，根据本文前述对误差的探讨，此时误差来源应该是信号处理、积分步长不同所致。为了分析这种差异所引入误差大小，本文计算了在仅输入加速度和仅输入速度时程时，模型2在地震动激励下的峰值误差最大值，如表7所示。由表7可知：在不同阻尼比下，最大误差不超过4.21%，仅设置加速度激励时误差最大。同时对比墩底约束处的位移、速度时程可知，原地震动已正确输入，在此不再赘述。据此建议，只要能保证桥墩底部的原始地震动时程等于激励地震动时程，均可达到较好的计算精度。同时，也可看出，信号处理的差异以及积分步长等的不同所造成的计算误差一般工程可接受的。

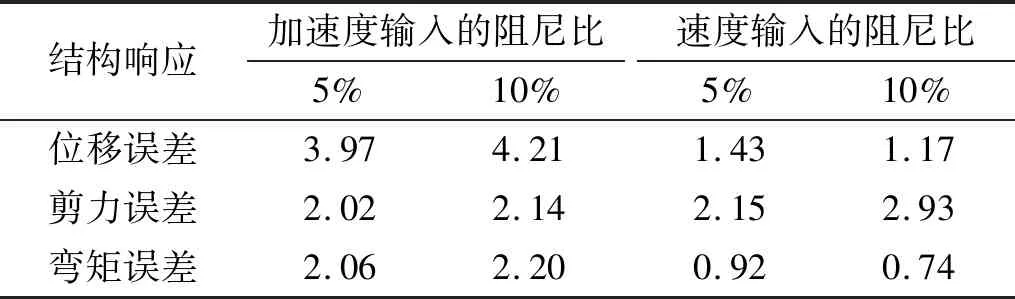
表7 不同时程信号输入时的误差最大值Tab.7 Maximum error of different input time history %

图8给出了TCU068地震动(考虑了2个墩的到时差和加速度幅值比为1∶0.75，2基底处存在不同幅值的残余位移)激励下，采用IDIM计算下的模型2桥墩1墩底剪力时程和墩顶位移时程，可以看出，改进的DIM也可以考虑残余位移和内力，对于跨断层桥梁同样具有适用性。

图8 结构响应时程Fig.8 Structural response time histories

步骤1对有限元模型施加恒荷载、静风压力或水流拟静力载荷后，分析非刚体模态特征是否合理以及恒载效应是否可以考虑。若可考虑则进行步骤2；若不合理或不能考虑(例如：底部约束释放引起变形回弹)，执行步骤3。理论推导可知，大质量法除了如下述大刚度法可能引入舍入误差外，还有源自式(2)右端第一项误差，故本文不建议使用。

步骤2明确大刚度法是否会导致计算失效或引入不可接受的舍入误差(一般施加大刚度取该方向总刚度的106倍)。若结构中无弱连接构件(小刚度的支座、支撑等)，也无屈服后可能发生刚体变位的组件，则可以采用大刚度法计算；否则进行步骤3。

步骤3建议采用DIM试算，检验程序对激励时程是否考虑了数值微分(通过对比约束处激励速度时程是否正确来判断)。若分析程序未考虑数值微分，则采用本文提出的IDIM进行计算(以I1-DIM分析即可)；若分析程序具备数值微分功能，尚应检验是否有不合理的激励信号分量产生，若有则需要滤波或信号处理后，以I2-DIM形式输入分析。

步骤4最后验证原结构底部的激励时程是否等于原始地震动时程。

4 结 论

本文针对位移输入法中存在的问题，为了方便其在有限元软件中的合理应用，在理论分析和对比校核的基础上得到了如下结论：

(1) 考虑Rayleigh阻尼，DIM存在不可忽略的计算误差，误差大小与输入地震动的类型和刚度比例阻尼系数β相关，且随着β的增大和脉冲效应的增强而增大，在分析中应引起注意。

(3) 明确了DIM类型计算误差——MRE方法对刚度比例阻尼系数较小的结构具有较好的适用性，但对于刚度比例阻尼系数较大的结构则不再适用性。本文建议了2种IDIM方法，对大跨度结构非一致激励反应分析均能够达到很好的计算精度。

(4) 综合多种算法的优劣，给出了分析空间非一致激励的结构响应分析流程，可以合理考虑非一致地震动潜在破坏性效应，且通用性强，计算准确度，建议采用。

后续将进一步探索非比例阻尼效应和地震动不确定性的影响等研究工作。