基于Bouc-Wen模型的阻尼器附加有效阻尼比解析解及应用

吴 山，何浩祥，王宝顺，陈建伟

(1.北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124;2.华北理工大学 建筑工程学院，河北 唐山 063210)

近年来，阻尼器作为典型的振动控制装置被广泛应用于建筑结构中，为主体结构提供附加阻尼和附加刚度，从而达到吸收外部激励能量并保护主体结构的目的。屈曲约束支撑(buckling restrained brace,BRB)和金属阻尼器等位移相关型阻尼器凭借减震机理明确、成本低廉及易于更换等优点在实际工程中被大量应用。

阻尼器在罕遇地震下主要凭借耗能减小结构响应，故耗能能力是其根本性能，而阻尼比是表征耗能能力的关键参数。建立计算各类型阻尼器附加有效阻尼比的精确方法从而量化阻尼器滞回耗能具有重要的理论和工程价值。GB 50011—2010《建筑抗震设计规范》[1]给出了附加有效阻尼比计算公式，但该方法是根据阻尼器在简谐激励下的变形能与结构总变形能的比值来计算的，通常是通过施加与结构主振动周期一致的简谐激励并达到预期位移时进行近似计算。该方法简单明晰，但精度偏低，需迭代试算，且并不完全适用于位移相关型阻尼器和磁流变阻尼器。此外，采用线性化等效法计算附加有效阻尼比的方法不能精确模拟结构非线性响应，也存在精度不高和计算繁复的不足。因此，亟需发展适合位移相关型阻尼器附加阻尼比的精确计算方法。

除了上述需求外，以BRB和金属阻尼器为代表的位移相关型阻尼器自身的恢复力模型精度也需要改进。JGJ 297—2013《建筑消能减震技术规程》[2]规定，位移相关型阻尼器可采用双线性恢复力模型模拟。基于双线性模型：吴克川等[3]提出了BRB消能减震结构的阻尼器滞回耗能计算公式；王维凝等[4]推导了铅阻尼器的滞回耗能公式。徐昕等[5]对计算BRB消能减震结构附加有效阻尼比的包络法、时变法计算精度进行了比较，发现包络法精度较低，计算结果偏保守，时变法精度更高，但计算繁复。有关研究表明，按滞回环面积相等原则，在预期位移下采用双线性模型对阻尼器滞回曲线进行拟合仅能保证当前条件下的准确性，而将拟合模型应用到其他位移时会产生较大偏差。Bouc-Wen模型是由微分方程描述恢复力的光滑曲线模型，具有可调性强、精度高等优点。相比双线性模型，Bouc-Wen模型可以模拟各类阻尼器恢复力的平滑屈服段，实现更精确表征，因此应用广泛。Cameron等[6]采用Bouc-Wen模型精确模拟了BRB的荷载-位移关系。黄金[7]采用双线性模型模拟BRB和主体结构性能，对BRB初始刚度、屈服后刚度比等参数对附加有效阻尼比的影响进行了分析，因需对主体结构弹性和弹塑性状态分别讨论，附加有效阻尼比无法统一表达。有鉴于此，高向宇等[8-9]建议采用改进的Bouc-Wen模型模拟BRB恢复力特性。研究结果表明：相比于双线性模型，Bouc-Wen模型在各级位移下的滞回耗能计算值具有更高的精度。李宗京等[10]提出针对阻尼器试验数据采用智能算法和Bouc-Wen模型进行精确拟合，但仍需采用数值计算方法获得阻尼比。以上成果表明，建立Bouc-Wen模型阻尼器的滞回耗能解析表达式可以为阻尼器的阻尼比精确计算提供严密的理论依据，具有重要的研究意义。吴从晓[11]曾利用积分方法对Bouc-Wen模型进行分段解析，但结果准确性欠佳。该问题的难点在于常用的Bouc-Wen模型公式是隐式形式[12-14]，基于传统形式并不能直接求出滞回环面积的精确解，无法准确表征阻尼器耗能。

有鉴于此，本文对Bouc-Wen模型进行显式化解析，推导不同参数取值情况下的耗能表征解析解，进而得到基于Bouc-Wen模型计算附加有效阻尼比的公式。结合试验数据对Bouc-Wen模型和双线性模型在模拟BRB耗能计算精度方面进行数值分析和对比，验证前者可以在各级位移下精确表征BRB耗能。对附加有效阻尼比进行参数分析，研究其变化规律和各性能参数的影响。最后，基于有限元模型，分析采用两种恢复力模型阻尼器对结构动力响应的影响。

1 基于Bouc-Wen模型的附加有效阻尼比计算公式

传统Bouc-Wen模型为隐式形式，可以由式(1)和式(2)表示

F(t)=αKD(t)+(1-α)KDyz(t)

(1)

式中：F(t)为系统恢复力；K和D(t)分别为系统的弹性刚度和轴向位移；α为屈服后刚度比；Dy为系统屈服位移；z(t)为无量纲内变量，满足方程

(2)

式中：A，γ和β为控制恢复力曲线外形的参数；λ为控制屈服尖锐程度。

1.1 Bouc-Wen模型显式化解析和耗能表征

上述的Bouc-Wen模型为隐式形式，难以得出滞回环面积的解析解，本文将对Bouc-Wen模型进行显式化解析。式(2)中，λ为决定模型屈服段尖锐程度的形状控制参数，λ越大，屈服段越锐利，趋近双线性模型，当λ取值较大时，可用双线性模型耗能表达式计算其滞回环面积，李建勤等基于30个防屈曲支撑的滞回曲线对模型参数进行了回归和分析，建议λ取0.4～2.5，并提出该参数对恢复力模型影响较小，在建议范围内取值模型形状差别不大，Cameron等和文献[15]分别采用Bouc-Wen模型模拟防屈曲支撑和剪切型金属阻尼器，其中λ均取1，模拟效果理想，可见当λ=1时采用Bouc-Wen模型可以较好地模拟防屈曲支撑等位移型阻尼器。因此，本研究中取λ=1并考虑参数条件，可得内变量z(t)和轴向位移D(t)之间的微分式为

(3)

下面根据γ和β的不同取值关系分别进行讨论。

(1) 当γ≠±β时，式(3)对D(t)积分可得

(4)

式中，D1为内变量z(t)=0时，轴向位移D(t)的值，该值可以通过内变量z(t)的反对称性z(a)=-z(-a)求出，其中a为加载幅值，即D1可以通过式(5)得出

(5)

至此，已实现对内变量z(t)的分段显式化解析，将式(4)代入式(1)可得Bouc-Wen模型显式化表达式

(6)

式(6)对D(t)求积分，得到滞回耗能Wc的表达式为

(7)

(2) 当γ=-β时，采用相同的方法求解，D1和Wc的解析表达式分别为

(8)

Wc=(1-α)KDy×

(9)

(3) 当γ=β时，D1和Wc的解析表达式分别为

(10)

Wc=(1-α)KDy×

(11)

1.2 基于Bouc-Wen模型附加有效阻尼比计算公式

GB 50011—2010《建筑抗震设计规范》给出的阻尼器附加给主体结构的有效阻尼比计算公式为

(12)

式中：ζa为阻尼器附加给主体结构的有效阻尼比；Wcj为第j个阻尼器在结构预期层间位移下往复循环一周所消耗的能量；Ws为设置阻尼器的减震体系在预期位移下的总应变能。不计及扭转影响时，设置阻尼器的减震结构在水平地震作用下的总应变能，可按式(13)估算

Ws=(1/2)∑Fiui

(13)

式中：Fi为质点i的水平地震作用标准值；ui为质点i对应于水平地震作用标准值的位移。

将消能减震体系等效成单自由度体系，阻尼器和主体结构的荷载-位移关系均采用Bouc-Wen模型表征，消能减震体系的位移记为x，阻尼器滞回耗能和减震体系总应变能如图1所示。

图1 阻尼器滞回耗能和减震体系总应变能Fig.1 Hysteretic energy dissipation of dampers and total strain energy of damping system

图1中，预期位移下阻尼器滞回耗能为滞回环面积，结构体系总应变能为三角形面积。阻尼器和消能减震体系的滞回关系均采用Bouc-Wen模型模拟，且假设两者γ和β的数值关系相同，以γ≠±β情况为例讨论阻尼器附加有效阻尼比公式，由于计算方法相同，限于篇幅不再讨论另外两种情况的表达式。

设预期位移为x，阻尼器的荷载-位移关系可表示为

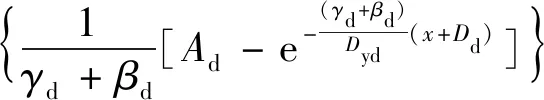
(14)

式中：Fd(x)为阻尼器预期位移为x时的阻尼力；Kd为阻尼器弹性刚度；αd为阻尼器屈服后刚度比；Ad，γd和βd为阻尼器Bouc-Wen模型的形状控制参数；Dyd为阻尼器屈服位移；Dd为式(1)中内变量z(t)=0时，阻尼器的位移，可以由式(5)求出，其中加载幅值a=x。主体结构的荷载-位移关系为

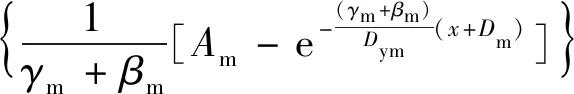
(15)

式中：Fm(x)为主体结构预期位移为x时的地震作用；Km为主体结构弹性刚度；αm为主体结构屈服后刚度和弹性刚度之比；Dym为主体结构屈服位移；Am，γm和βm为主体结构Bouc-Wen模型的形状控制参数；Dm为式(1)中内变量z(t)=0时，主体结构的位移，可以由式(5)求出，其中加载幅值a=x。消能减震体系的恢复力关系为阻尼器和主体结构荷载-位移关系的叠加，可以表示为

Fs(x)=Fd(x)+Fm(x)

(16)

式中，Fs(x)为消能减震体系预期位移为x时的地震作用。

可得阻尼器附加有效阻尼比为

(17)

当主体结构为线性时，式(17)中Fm(x)改为

Fml(x)=Kmx

(18)

需要说明的是：在式(17)中假设主体结构荷载-位移关系为Bouc-Wen模型和线性关系是便于下文进行参数分析，实际工程中的减震结构总应变能应通过结构响应计算得到。

1.3 解析解精确性验证

为了验证本文提出的基于Bouc-Wen模型的能量表征和附加有效阻尼比公式的准确性，假设在某减震结构体系中设置了三种不同参数的阻尼器，主体结构和阻尼器采用Bouc-Wen模型模拟。采用前文解析解和梯形数值积分法(数值方法)分别求预期位移为10 mm下的阻尼器耗能和附加有效阻尼比，并统计误差，其中Dym取1 mm，Dyd取0.2 mm，αd和αm取0.05，Km取500 kN/mm，Kd取470 kN/mm，Ad和Am均为1，γm取0.45，βm取0.55，阻尼器其余模型参数取值、阻尼器耗能表征和附加有效阻尼比结果，如表1所示。由表1可知，解析解结果和数值解结果十分接近，验证了解析解的正确性。

表1 不同参数下模型耗能及阻尼比误差Tab.1 Errors of dissipated energy and damping ratio of different models

2 基于Bouc-Wen模型和双线性模型的附加有效阻尼比精度分析

根据JGJ 297—2013《建筑消能减震技术规程》，BRB等位移相关型阻尼器宜采用双线性恢复力模型进行模拟。吴克川等基于双线性模型对BRB的附加有效阻尼比计算方法及变化规律进行了解析研究，提出双线性模型模拟的滞回环面积可按式(19)计算

Wc=4DbKb(1-αb)(x-Db)

(19)

式中：Wc为阻尼器在预期位移x下滞回一周所耗能量；Db，Kb和αb分别为双线性模型中阻尼器的屈服位移、弹性刚度和屈服后刚度比。

然而，双线性恢复力模型只是阻尼器恢复力-位移关系的近似表征，以滞回环面积相等为原则，采用双线性模型在预期位移下拟合阻尼器滞回环，在预期位移下可以做到面积相等，但仍采用该模型表征其他位移下阻尼器耗能则存在较大误差。为验证双线性模型的局限性，采用双线性模型和Bouc-Wen模型分别对BRB滞回试验数据进行了拟合，并对其能量表征精度进行对比。Cameron等对5个BRB试件进行了低周滞回试验，各试件试验结果均可采用，在此选取试件00～12的滞回曲线。试验采用位移控制，分16 mm，32 mm和48 mm三级加载，采取滞回环面积相等原则在预期位移32 mm下对滞回曲线进行拟合，对比采用的双线性模型和Bouc-Wen模型在16 mm和48 mm下的滞回环面积与试验滞回环面积的误差。结果表明，双线性模型参数取值具有不唯一性。因此，选取两个双线性模型与Bouc-Wen模型对比，两种恢复力模型参数取值如表2所示。表2中：BW为Bouc-Wen模型；BL1和BL2为两种双线性模型。拟合效果如图2所示，各模型在各级位移下表征的能量及误差，如表3所示。

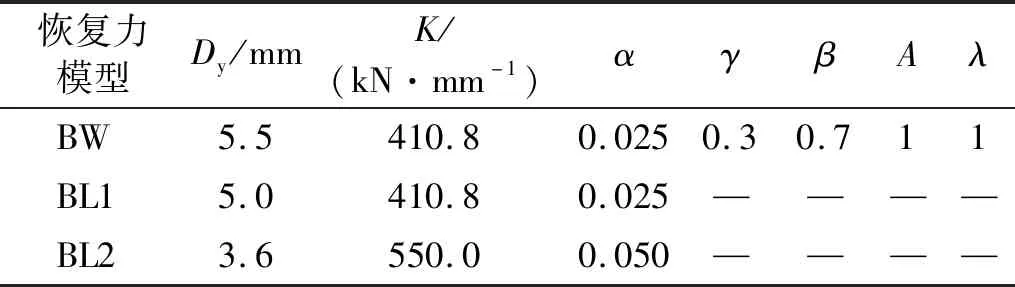
表2 恢复力模型参数取值Tab.2 Parameter value of hysteric model

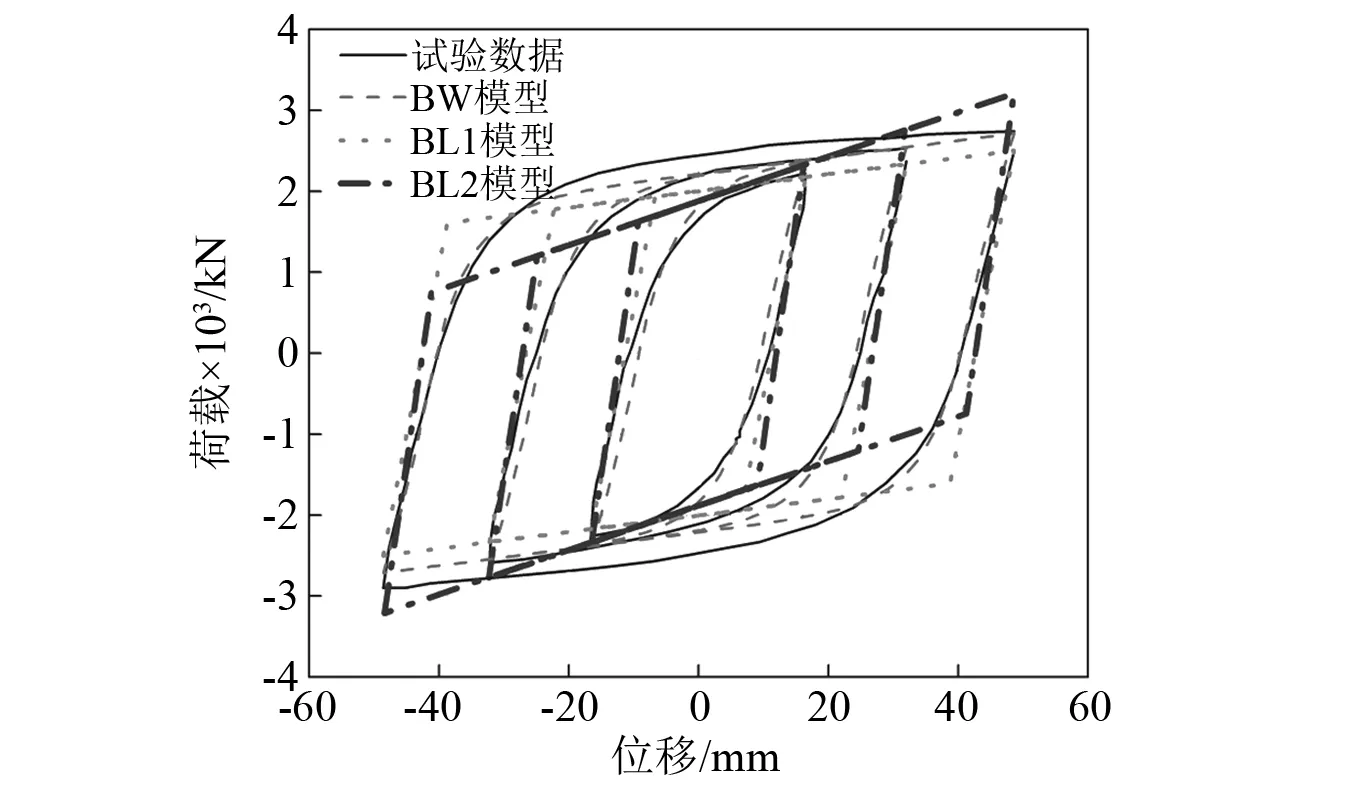
图2 各恢复力模型拟合效果Fig.2 Fitting effect of hysteretic models

表3 不同位移下恢复力模型能量表征及误差Tab.3 Energies and errors of hysteretic models under different displacements

BW模型在各级位移下拟合误差均在5%以内，而双线性模型在预期位移下拟合误差较小，但其他位移下误差明显增大，α是影响双线性模型拟合精度的关键，BL1选取的α与BW相同，但平均误差仍达到11.3%。由此可知，与双线性模型相比，Bouc-Wen模型可以在各级位移下更精确地表征阻尼器耗能。采用Bouc-Wen模型计算阻尼器附加有效阻尼比时具有优势：①阻尼器提供给结构的附加有效阻尼比与结构层间位移相关，由于某一时刻下结构各层层间位移不尽相同，因此，基于Bouc-Wen模型得到的结构附加有效阻尼比精度更高；②结构层间位移随时间改变，因此，Bouc-Wen模型适合求解时变附加有效阻尼比。

3 附加有效阻尼比参数分析

Cameron等根据BRB拟静力试验结果，采用Bouc-Wen模型对试件的恢复力模型进行了模拟，其中γd=0.45，βd=0.55。由此可知，γd≠±βd的情况是采用Bouc-Wen模型模拟BRB和软钢阻尼器恢复力模型时常遇的情况。因此，对此种情况下阻尼器附加有效阻尼比的各参数影响进行分析。

阻尼器和消能减震体系的滞回关系均采用Bouc-Wen模型模拟，对阻尼器和主体结构屈服后刚度比的比值αd/αm、弹性刚度比Kd/Km、屈服位移之比Dyd/Dym和阻尼器滞回环形状控制参数之比γd/βd对阻尼器附加有效阻尼比ζa的影响进行分析，结果如图3所示，其中结构位移比为结构位移和结构屈服位移之比。Dym取1 mm，Dyd取0.2 mm，αd和αm取0.05，Km取500 kN/mm，Kd取470 kN/mm，γd和γm均为0.45，βd和βm均为0.55，Ad和Am均为1，进行参数分析仅改变该参数比值的分子，同时保证γd+βd=1，γm+βm=1，其他参数不变。

图3 主体结构为非线性时附加有效阻尼比参数分析Fig.3 Parameter analysis of additional effective damping ratio when structure is nonlinear

可见附加有效阻尼比ζa随结构变形增大的变化趋势可以分为3个阶段：①线性上升阶段，当结构变形较小时，ζa随着结构变形增大而线性增大；②非线性上升阶段，当变形达到一定程度时，ζa仍随结构变形增大而非线性增长，但增长速率变缓，并最终达到峰值点；③线性下降阶段，ζa达到峰值点之后，结构变形继续增大，ζa开始缓慢下降，其最终值在峰值的50%以上，下降速率与参数αd/αm和γd/βd的取值有关。设ζa在3个阶段的变化速率分别为Vn1，Vn2和Vn3，增大各参数数值对Vn1，Vn2和Vn3的影响如表4所示。

表4 性能参数对ζa变化速率的影响规律Tab.4 Effect of performance parameters on variation rate of ζa

当主体结构线性，对阻尼器和主体结构弹性刚度比Kd/Km、阻尼器屈服位移Dyd进行参数分析，结果如图4所示。参数分析中各参数取值同主体结构为非线性时。附加有效阻尼比与主体结构为非线性时具有相同的变化趋势，但下降速率更快，屈服位移对附加有效阻尼比峰值没有影响。

图4 主体结构为线性时附加有效阻尼比参数分析Fig.4 Parameter analysis of additional effective damping ratio when structure is linear

由以上结果可知，通过提高BRB和金属阻尼器的截面尺寸等方式提高其初始刚度、屈服力，或使其滞回曲线更饱满，可以为主体结构提供更大的附加有效阻尼比，从而使结构体系具备更好的减震效果。

当阻尼器屈服位移过小时，附加有效阻尼比将更快到达峰值，但峰值较小，即有利于在小震下减震，但中大震下减震效果不理想。因此，应将阻尼器的屈服位移设置在合理范围内。

4 结构算例分析

为了进一步验证基于Bouc-Wen模型计算阻尼器附加有效阻尼比的精度和可行性，对比不同阻尼器恢复力模型对结构响应的影响，选取一典型钢筋混凝土框架结构进行计算分析。该框架结构共8层，每层高度4 m，共32 m高。7度抗震设防，场地类别为Ⅱ类，抗震等级为一级。设计地震分组为第二组，设计基本地震加速度值为0.15 gal。框架梁截面尺寸为700 mm×1 000 mm，采用C30混凝土，弹性模量为3.0×104MPa，抗压强度标准值为20.1 MPa，配筋钢筋弹性模量为2.0×105MPa，屈服强度为413 MPa，极限强度为620 MPa，配筋率为0.96%；框架柱截面尺寸为900 mm×900 mm，采用C35混凝土，弹性模量为31 500 MPa，抗压强度标准值为23.4 MPa，采用与框架梁相同的钢筋，配筋率为1.62%。基于SAP2000建立如图5所示有限元模型，梁柱采用杆系单元模拟，弹塑性变形用塑性铰单元模拟。结构第一周期为0.556 s。

图5 框架结构有限元模型Fig.5 Finite element model of frame structure

框架每层沿X，Y两水平方向各布置4个金属屈服型阻尼器。为探究采用不同恢复力模型模拟阻尼器而造成的结构响应差异，共设置3个结构进行对比分析，三者主体结构相同，固有阻尼比为0.05，TH0采用Bouc-Wen模型阻尼器，初始刚度取600 kN/mm，屈服位移为1.67 mm，屈服后刚度比取0.01，γ和β均为0.5，A和λ均为1。TH1和TH2的阻尼器为双线性模型，采用不同的参数对TH0阻尼器的Bouc-Wen模型在预期位移20 mm下拟合，拟合效果如图6所示，参数取值和拟合误差如表5所示，其中TH0的阻尼器恢复力模型在20 mm下表征的滞回能量为71 022 J。

表5 双线性模型参数取值及拟合误差Tab.5 Parameter values and fitting errors of bilinear models

图6 双线性模型拟合效果Fig.6 Fitting effect of bilinear models

在结构主方向(Y方向)输入El Centro波，将峰值加速度(peak ground acceleration，PGA)分别调幅至55 gal(小震)、150 gal(中震)和310 gal(大震)进行分析[16-17]。小震下在响应峰值较大时段(0～10 s)的顶层绝对位移和绝对加速度时程，如图7所示。

图7 TH0，TH1和TH2顶层响应时程Fig.7 Time history of top story response of TH0,TH1 and TH2

Bouc-Wen模型可以在各级位移下精确表征阻尼器耗能，故视TH0为准确结果。与TH0相比，TH1和TH2的时程响应绝对值之和误差与响应峰值误差可分别按式(20)和式(21)计算

(20)

(21)

式中：et和ep分别为时程响应绝对值之和误差与响应峰值误差；Ai为第i个时间点TH1或TH2的结构响应值；Bi为第i个时间点TH0的结构响应值；Ap为TH1或TH2的结构响应峰值；Bp为TH0的结构响应峰值，结构响应包括位移和加速度；N为地震动时程中时间点个数。不同PGA下两种误差计算结果，如图8所示。TH1和TH2的层间位移、层间剪力和各层绝对加速度幅值的误差，如图9所示。由结果可知，采用双线性模型模拟阻尼器性能将产生较明显的响应误差，中小震下的误差更为显著，原因在于中小震下阻尼器耗能能力有明显区别，根据图6，小位移时Bouc-Wen模型由于屈服段平滑，和两种双线性模型相比包络面积区别较大，所以中小震下结构响应区别显著，而大震下结构位移响应与拟合预期位移相近，各恢复力模型包络面积相差无几，故结构响应差别不大。此外，对于较低楼层，结构加速度响应误差较大；对于较高楼层，结构的层间位移和剪力误差较大。

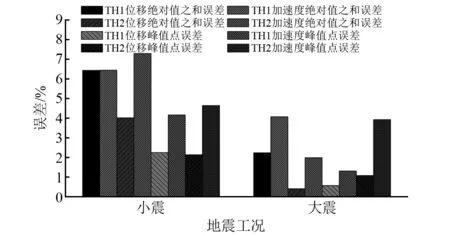
图8 TH1和TH2响应时程误差Fig.8 Error of response time history of TH1 and TH2

图9 TH1和TH2响应幅值误差Fig.9 Error of response amplitude of TH1 and TH2

为了验证基于Bouc-Wen模型的阻尼器附加有效阻尼比计算方法精度，以TH0结构响应幅值作为计算附加有效阻尼比的标准，得到不同结构在不同强度地震动下的附加有效阻尼比，结果如图10所示，层间位移需按式(22)转化为阻尼器位移

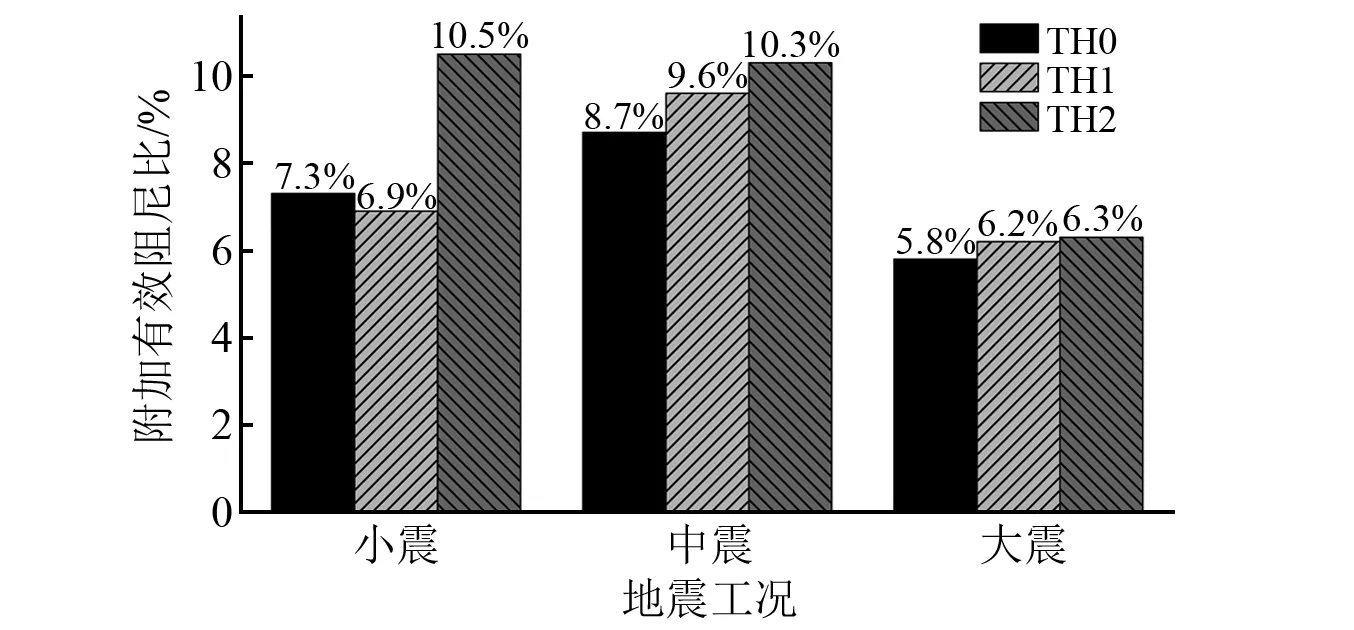
图10 TH0，TH1和TH2附加有效阻尼比Fig.10 Additional damping ratio of TH0，TH1 and TH2

a=xcosθ

(22)

式中：a为阻尼器位移；x为结构层间位移；θ为阻尼器与框架梁夹角。本算例中cosθ取0.85。

由结果可以看出，由于TH1和TH2拟合预期位移是20 mm，因此，在大震下和TH0附加有效阻尼比差别较小，但在中小震下存在较大误差，其中小震下TH2的误差达到43.8%，说明双线性模型仅在拟合预期位移左右计算附加有效阻尼比有较高精度，在其他位移下精度并不理想。此外，TH0和TH1附加有效阻尼比的变化规律是随着PGA增大先增后减，而TH2则持续下降，可见由于拟合参数取值具有不唯一性，由双线性模型得到的阻尼比变化规律不一致、不准确，且易高估阻尼器的减震性能。因此，基于Bouc-Wen模型计算附加有效阻尼比在精度和稳定性上均优于双线性模型。

综上，采用Bouc-Wen模型和双线性模型计算阻尼器提供给结构的附加有效阻尼比时，结果存在一定差异，尤其是当阻尼器位移与拟合预期位移差异较大时应重视该现象。对于滞回曲线更接近于Bouc-Wen模型的阻尼器，宜选择该模型而不是双线性模型并根据本文提出的解析方法来进行阻尼器的滞回耗能和阻尼比计算、参数设计及减震结构建模和动力分析。

5 结 论

采用Bouc-Wen模型表征位移相关型阻尼器的滞回特性及阻尼比具有良好的精度，针对该模型的特性及隐式表达的局限性，本文对基于Bouc-Wen模型的附加有效阻尼比计算公式进行了解析推导，并对附加有效阻尼比变化规律、参数灵敏度及对结构响应的影响进行了分析。相关结论如下：

(1) 本文提出的基于Bouc-Wen模型的附加有效阻尼比计算公式在不同位移下均有较高的精度，而双线性模型仅仅在预期位移下能较准确算得附加有效阻尼比，在其他位移下精度较差，且由于参数取值具有不唯一性，难以稳定地体现附加有效阻尼比随结构位移的变化规律。

(2) 对于阻尼器本身而言，采用Bouc-Wen模型和双线性模型算得的附加有效阻尼比有一定的差异，在阻尼器设计和优化时应优先采用Bouc-Wen模型。对于采用阻尼器的减震结构体系而言，采用不同恢复力模型的阻尼器造成的结构动力响应差异相对弱化，但对于中小震下的减震分析和顶部楼层响应而言，应重视选用双线性模型引起的误差。

(3) 附加有效阻尼比随结构位移先增后减，呈抛物线状，变化过程大体可分为3个阶段：线性上升阶段、非线性上升阶段、线性下降阶段。初始刚度更大、屈服后刚度更小、极限承载力更高且恢复力模型更饱满的阻尼器，可以为主体结构提供更大的附加有效阻尼比，使结构体系达到更好的减震效果。当阻尼器屈服位移较小时，附加有效阻尼比将更快到达峰值，但其值较小，有利于在中小震下减震，但大震下减震效果不理想。依据Bouc-Wen模型计算精确的阻尼器阻尼比有利于阻尼器的精细化设计和性能提升。