二元复合材料板的自由振动:半解析法1)

薛 坚 牛牧青 张文勇 陈立群

(哈尔滨工业大学 (深圳)理学院,广东深圳 518055)

引言

板结构广泛应用在航空、航天、航海以及建筑工程等领域[1-3].由于薄板结构“轻”和“薄”的特性,其相对其他构件来说更易产生振动[4].结构振动带来的危害不容忽视.在交通运输领域,振动会降低结构的安全度和乘客的舒适度[5].在航空航天领域,振动会影响航天器的工作性能,甚至引发安全事故.比如,有些火箭发射失利是由于振动引发的故障.在工程实践中,当外激励频率接近板结构的固有频率时,会出现共振现象.因此在板结构设计期间应考虑的重要因素之一是它们的振动特性[6-9].研究板结构固有频率和振型等振动特性,对结构安全有效地运行具有重要的意义.

超材料中可调控的振动带隙为结构的减振提供了新思路[10-12].从实际材料和结构出发,通过对结构自身结构形式和材料进行合理设计,可以得到低频的局域共振带隙[13-16].相对于超材料结构,二维的二元或三元周期结构不需要附加其他构件,也不影响与其他结构的连通性.通过改变二元板结构的材料参数和几何构型可以调整带隙位置和带宽.目前针对二元或三元超材料板的研究工作主要集中在振动带隙的计算和分析上[17-18],研究的方法目前主要有平面波展开法[19-20]、有限元法[15]、有限差分法[21]等数值方法.而探究超材料板中局域共振单元的固有频率和振型,能清晰、直观地了解结构的振动特性,为结构和材料的设计提供理论依据.

二复合材料板一般由材料参数差异较大的硬材料和软材料构成.通过设计复合材料在板面内的分布,可以改善结构的振动特性.然而,这种非均匀设计也增大了板结构分析的困难.在分析梁板结构自由振动问题的方法中,比较常见的有改进傅里叶法、伽辽金法、区域分解法、里兹法等等.里兹法是一种基于能量变分的近似方法,在研究结构的力学特性方面表现出高效,易实施等特点[22-23].近几年来,研究者们利用里兹法对各种非均匀板结构进行了研究,例如阶梯/加筋板[24-26]、带孔板[27-28]、裂纹板[29-33].在Ritz 法实施过程中,最关键的一步是构造能合理描述结构特性且满足边界条件的试函数.Gao等[25]将雅克比正交多项式和三角级数作为位移场的试函数,并利用雅克比-里兹法研究了阶梯环形和圆形板的振动响应.Chan 和Tai[26]基于里兹法对阶梯Mindlin 板进行建模,利用分层高阶梁单元获得位移场的试函数,得到的结果比使用均匀梁函数的精度更高.Deng 等[27]以雅克比多项式作为试函数,在Ritz 法的框架下建立了声学黑洞压电悬臂梁的半解析模型.Huang 等[29]将裂纹函数和多项式组合成裂纹板位移场的试函数,并利用带特殊试函数的Ritz法研究了含裂纹功能梯度板的自由振动.Xue 和Wang[30]构造了含裂纹加筋板位移场的试函数,并研究了裂纹参数和筋条参数耦合作用下对结构频率和振型的影响规律.据作者所知,迄今为止没有可用的解析模型可以分析二元复合材料板的自由振动.由于硬材料和软材料在板平面内的非均匀分布,直接使用带有传统全局试函数的Ritz 方法来研究该结构的振动特性可能会遇到收敛性和计算效率方面的问题.

本文针对含有方形嵌入体二元复合材料板的自由振动问题,建立结构的半解析模型,分析几何构型对板振动特性的影响规律.根据二元材料的分布,将二维平板分解成两个区域,分别构建各区域的动能和势能.通过在板位移场中附加区域试函数,来合理描述板内材料参数巨大差异导致的局部位移非光滑性.基于两区域的边界条件,构造位移场的试函数.利用里兹法求得不同嵌入体尺寸和位置下板的固有频率和振型.

1 理论建模

1.1 模型描述

通过在刚度较大的矩形基体板中嵌入一个低刚度矩形子板,得到二元复合材料板(如图1 所示).根据材料参数的不同,将基体和嵌入体定义为板的两个子区域①和②.将笛卡尔坐标系的原点o建立在二元复合材料板的中点.板在x和y方向的尺寸分别为a和b,矩形嵌入体在x和y方向的尺寸分别为a1+a2和b1+b2.

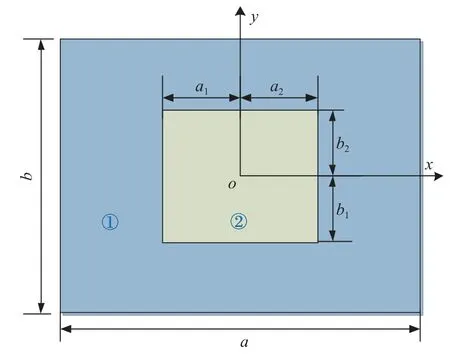
图1 二元复合材料板的几何形状和尺寸Fig.1 Geometry and dimension of binary composite plates

1.2 结构势能和动能

在自由振动的分析中,存储在体积为V的弹性体内应变能为

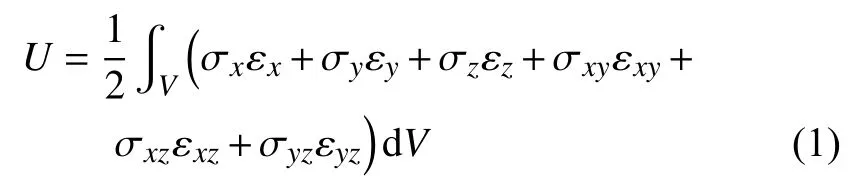
其中 εx,εy,εz,εxy,εxz,εyz是应变分量,σx,σy,σz,σxy,σxz,σyz是应力分量.

基于薄板理论,板的应变能为

根据本构关系,对式(2)在厚度z方向上积分,二元复合材料板两个子区域的势能可表示成与横向位移w(k)(x,y)相关的函数

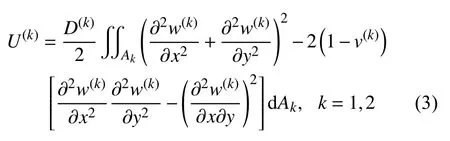
其中,Ak表示子区的中面,D(k)=E(k)h3/[12(1-v(k))2]是抗弯刚度,E(k)是子区材料的弹性模量,v(k)是泊松比,h是板的厚度.

根据运动学假设,密度为 ρ 物体的动能为

其中,ρ(k)是每个子区的材料密度;分别表示板面内位移和横向位移对时间的一阶导数;对于横向振动的板,式中的=0.在厚度z方向积分之后,式(4)退化成

二元复合材料板各子区的动能可表示成

1.3 边界条件和振型函数

根据两子区连接处的变形协调条件构造位移场的振型函数是本文研究的关键步骤之一.对于均质材料板,假设的振型函数只要线性无关且满足基本边界条件即可.而二元复合材料板中两子区的材料参数具有数量级差异.传统振型函数中多项式组合很难模拟刚度突变引起局部位移的非光滑性.本研究基于两子区的边界条件,通过在振型函数中附加区域试函数,来描述板内材料参数差异性导致位移或转角的突变.

本文所提出方法适用于简支、悬臂和自由等多种边界条件.为简明起见,选取最常见的四边简支(SSSS)作为板的边界条件.

对于SSSS 矩形板,其位移边界条件为

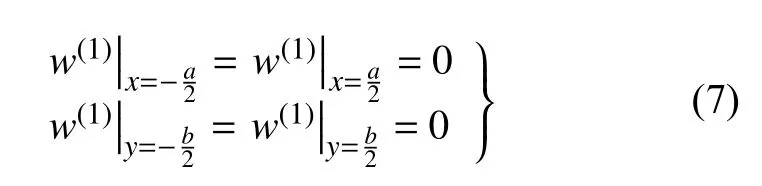
两子区在连接处的位移和转角协调条件为

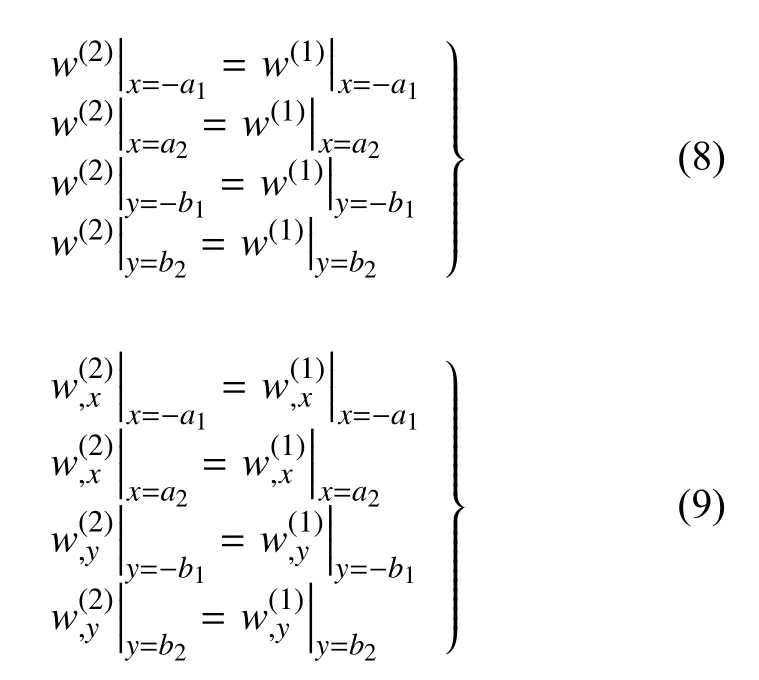
后文的Ritz 法求解需要选择合适的线性无关且满足本质边界条件位移场试函数,以保证解的精度.综合考虑计算的稳定性、效率和结果的收敛速度等方面,本文选取切比雪夫多项式作为振型函数的基函数来计算二元复合材料板的固有频率和振型.

切比雪夫多项式是正交多项式中比较常用的一种,一维切比雪夫多项式可以表示为

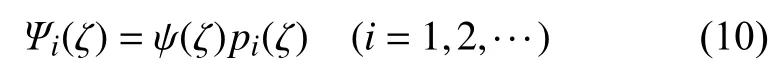
这里的 ψ(ζ)是与边界条件相关的函数,使得每个多项式 Ψi(ζ)都满足任意的边界条件;pi(ζ)是基函数,其表达式为

令式子中的 ζ 等于2x/a,即可得到x方向的基函数

同理,令 ζ=2y/b就得到y方向的基函数

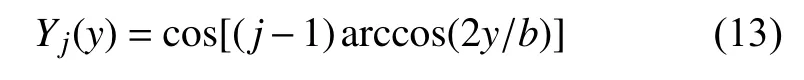
各个子区的横向位移可以假设成

其中 ψ(x,y)和χ(x,y)分别是和边界条件和变形协调条件相关的函数.χ(x,y)具体表达式为

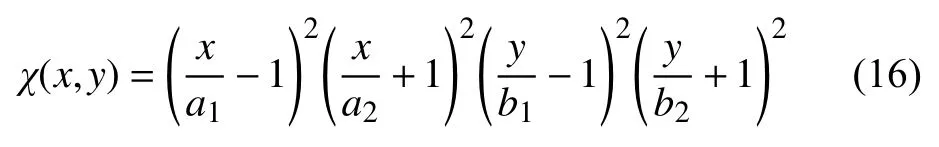
ψ(x,y)在不同的边界条件下有不同的表达式,在SSSS 的边界条件下,其表达式为

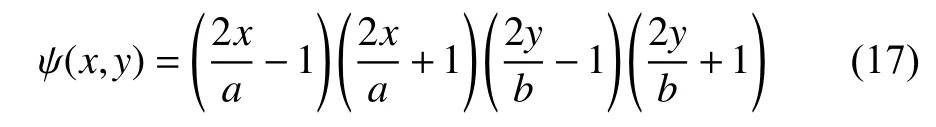
1.4 里兹法

本研究应用Ritz 法来计算板的固有频率和模态.二元复合材料板的总能量为

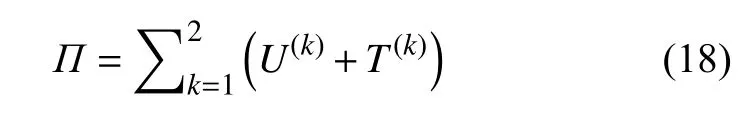
将振型函数式(16)和式(17)代入到势能式(3)和动能式(6)之后再代入到板的总能量(18)中,然后分别对每一个待定系数求偏导数得到相应的方程组

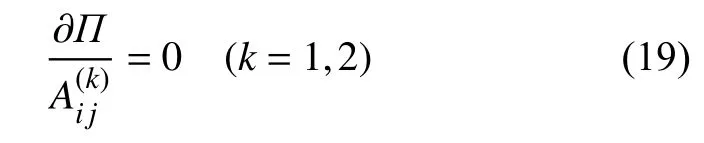
这里将振型函数里所有的待定系数组成一个向量,向量的维数等于所有待定系数的总数=I×J+M×N,且q=.方程组(19)可以转换成

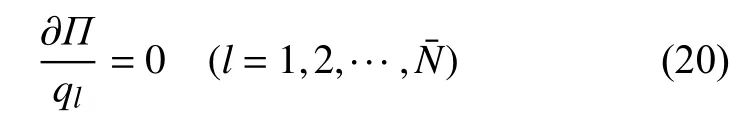
从而导出一个特征值问题

其中K和M的元素可表示为

通过求解方程(21)得到的特征值和特征向量分别对应的就是板的固有频率和模态.

2 结果分析

利用前文提出的方法,可计算不同边界条件下任意两种材料组成的二元复合材料板的固有频率和振型.通过参数分析,研究嵌入体的几何构型和材料参数对板振动特性的影响规律.本文分别选取弹性模量较小的环氧树脂和弹性模量较大的Al2O3作为嵌入体和基体.具体材料参数为:E(1)=403 GPa,ρ(1)=3986 kg/m3,υ(1)=0.23,E(2)=4.35 GPa,ρ(2)=1180 kg/m3,υ(2)=0.37.

2.1 收敛分析及有限元验证

在Ritz 法中,随着试函数项数的增加,所得到的结果越来越接近于精确解.表1 通过改变式(14)和式(15)中全局试函数I和J以及区域试函数M和N的值,并求解方程(21)得到二元复合材料板固有频率(l表示阶数),来验证本文提出方法的收敛性和准确性.其中,全局试函数里的I和J均取10,12,14,15 或16 而区域试函数M和N均取0,2,3,4,5 或6,M×N取0 表示没有附加区域试函数.板中嵌入体的几何尺寸为:a1=a2=0.2a,b1=b2=0.2b.为对比起见,采用ABAQUS 里的S4 R 壳单元建立了二元复合材料板的有限元模型,并共划分了2511 个网格.

根据表1,当附加函数项数M=N=0 时,随着全局试函数I和J的增加,前五阶固有频率逐渐收敛到一个稳定值.当I×J分别取15×15 和16×16 时,第一阶和第四阶频率已经分别稳定在87.54和329.8,其他阶的频率变化不超过0.5%.值得注意的是:尽管传统的全局试函数展现出一定的收敛性,但是收敛到的结果不一定是正确的;尤其是第四阶频率,使用全局试函数(I和J均取15 或16)得到的结果与有限元仿真结果差异极大(大于30%);然而,附加区域试函数可以大大提高计算效率和结果准确性,I×J和M×M分别取15×15 和4×4 时,结果与有限元结果的误差几乎等于0.从表1 中可以看出:区域试函数M=N=2 时,第四阶和第五阶固有频率快速降低,并且已经收敛于精确解;而且随着附加区域试函数项数M×N增加到4×4 时,各阶频率都收敛到一个稳定的值.通过与Abaqus 仿真结果对比,理论解与有限元法结果非常吻合,前五阶频率中最大误差为3.6%,从而验证了本文所提出方法的正确性.

表1 二元复合材料板固有频率的收敛性分析Table 1 Convergence of natural frequencies for the binary composite plates

图2 给出了表1 中前五阶固有频率对应的振型图.将本文方法得到的振型图与有限元结果进行比较,两者吻合良好.从图中可以看出,第四阶振型出现了明显的振动局部化,即嵌入体部分的位移较大,而基体板的位移非常小.这是因为基体板的刚度远大于嵌入体的刚度导致的.此外,前面表1 中的收敛分析可知,仅使用全局试函数得到的第四阶固有频率无法收敛到一个准确的结果.这是因为传统的全局试函数很难描述复合材料板面内刚度突变以及振动局部化问题.而附加区域试函数则是解决该问题的一个非常有效的途径.

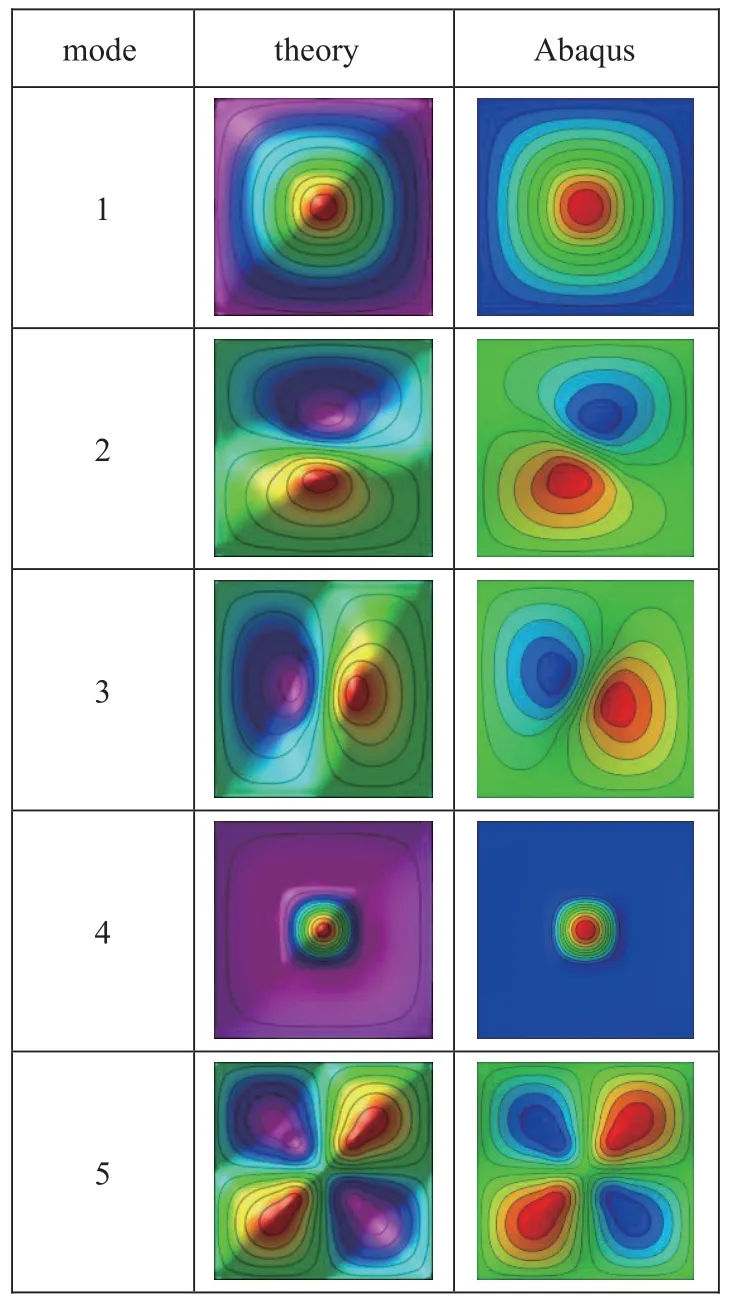
图2 二元复合材料板前五阶振型图Fig.2 First five modes of binary composite plates

2.2 几何尺寸分析

图3 考察了嵌入体尺寸为a1=a2=0.25a,b1=b2=0.25b时板前两阶横向位移和转角的振型图,图中同时给出了振型的二维和三维视图.和图2 中的振型对比可以看出:随着嵌入体面内几何尺寸增大,其固有频率减小,局部振动振型从第四阶变成第二阶,振动局部化的区域也增大了.实际上二元复合材料板的振型可以看成是基板和嵌入体振型的耦合.而具有明显振动局域化的振型以及对应的频率主要和嵌入体的几何尺寸和材料参数有关.对单个矩形板来说,它的长宽和固有频率是直接成反比的.因此,嵌入体面内几何尺寸增大会显著降低局域共振发生的频率,所对应的振型阶数也会发生改变.图4 给出了一阶振型(w)、转角(w,x)以及应变(w,xx)在x=0处的截面图.从图4 和图3 中转角三维振型图可以看出,在基体和嵌入体的连接处出现了明显的非光滑现象,尤其是应变在y/b=0.25 处发生了突变.两种不同嵌入体尺寸板的前两阶振型截面图(x=0)在图5 中给出.从图5 可以看出嵌入体尺寸越大,各阶振型中局部的不光滑性就越明显.

图3 二元复合材料板振型图Fig.3 Modes of binary composite plates

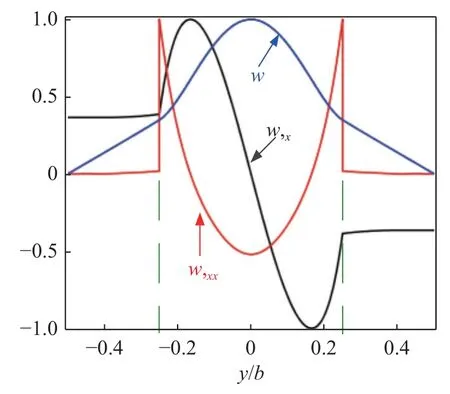
图4 位移、转角和应变的截面图(x=0)Fig.4 Sectional view of displacement,rotation and strain (x=0)

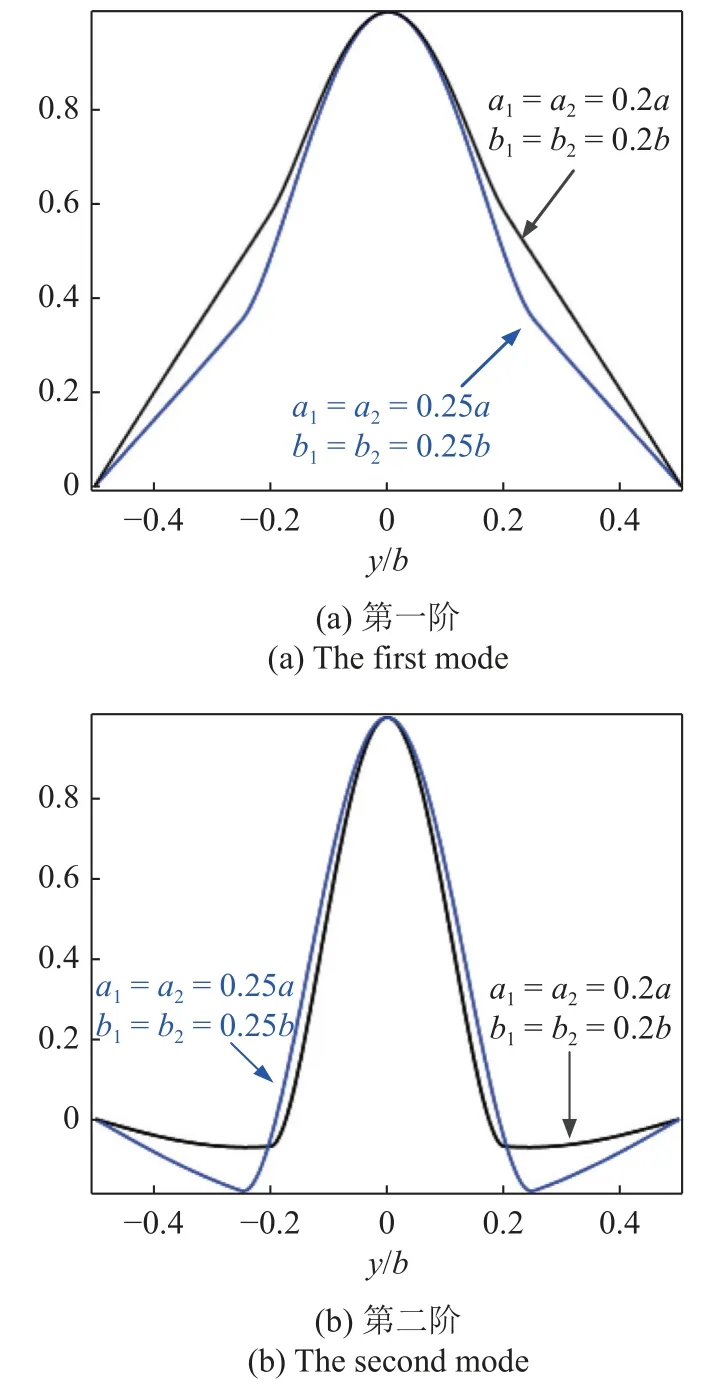
图5 不同嵌入体尺寸下板振型截面图(x=0)Fig.5 Cross-sectional views of the modes of the plates with different inlay sizes (x=0)

2.3 嵌入体位置研究

图6 和图7 分别考察了不同嵌入体位置下二元复合材料板的固有频率和振型.case A 表示嵌入体的中心与板的中心重合,其几何尺寸与2.1 中的算例保持一致.case B 和case C 中嵌入体的几何尺寸分别为a1=0.3a,a2=0.1a,b1=0.1b,b2=0.3b和a1=0.2a,a2=0.2a,b1=0.1b,b2=0.3b.从固有频率对比(如图6)可以看出:嵌入体位置对低阶频率的影响比高阶频率要小,嵌入体位置在一定范围内的变化对一阶固有频率的影响可以忽略不计.这是因为嵌入体位置的变化不会影响二元复合材料板整体的刚度,因此对结构的固有频率影响较小.结合图2 和图7,通过对比三种情况下板的振型,可以得出嵌入体的位置对振型影响比对固有频率的影响更明显,尤其是第二阶振型.因为对基体板而言,嵌入体的刚度非常小,因此嵌入体所在的位置更容易出现较大的位移.将三种情况下的第二阶和第四阶振型对比发现:嵌入体的位置决定了振动模态中振动节线和位移最高点的分布,即可以通过改变嵌入体的位置调整振动局部化的位置.

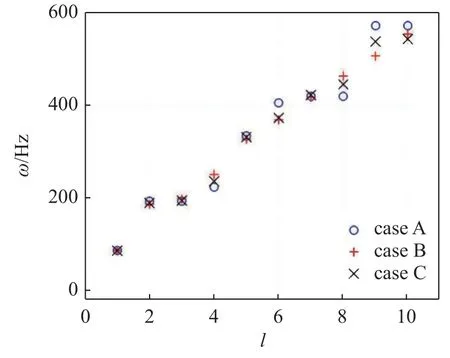
图6 不同嵌入体位置下二元复合材料板固有频率Fig.6 Frequencies of the plate with different inlay locations

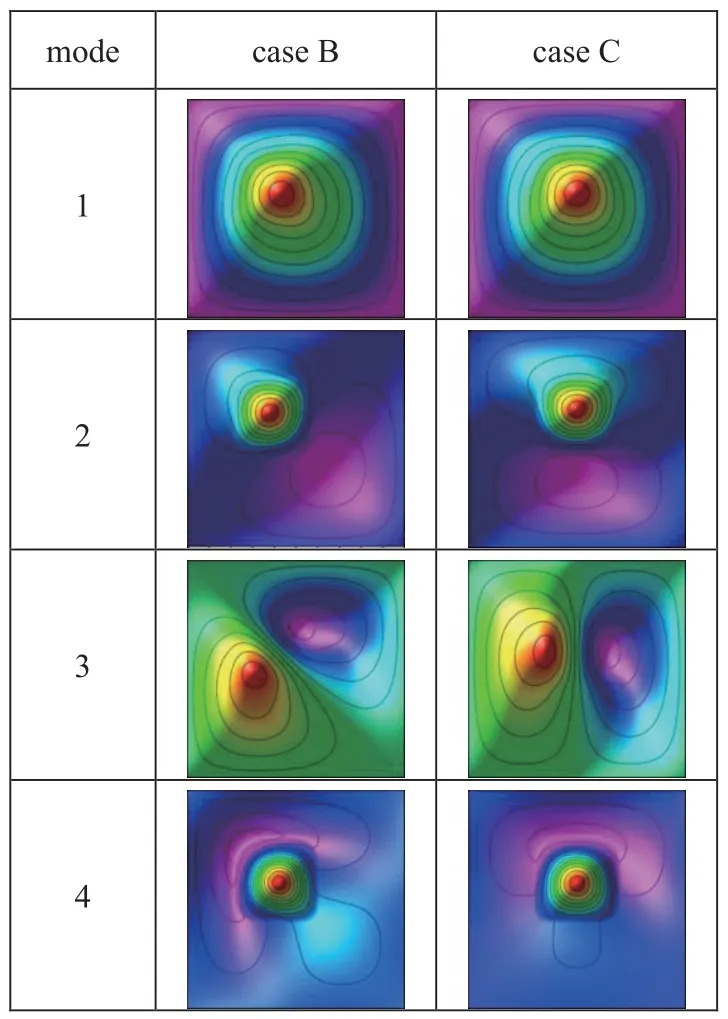
图7 不同嵌入体位置下二元复合材料板的振型Fig.7 Modes of the plate with different inlay locations

3 结论

本文建立了二元复合材料板自由振动的半解析模型,并通过有限元分析验证了理论方法与结果的正确性.通过参数分析,探究了嵌入体几何尺寸和位置对结构固有频率和振型的影响规律,并得到以下结论.

(1)通过在位移的振型函数中附加区域试函数,可以合理描述复合材料板面内刚度突变引起局部位移、转角和应变的非光滑性.

(2)在利用里兹法分析具有振动局部化的模态时,使用全局试函数会得到不准确的结果,而附加区域试函数可以显著提高收敛速度以及结果的准确性.

(3)嵌入体和基体材料参数的差异性会导致二元复合材料板出现明显的振动局部化.振型中振动局部化的位置由嵌入体的位置决定.具有该现象振型阶数随着嵌入体尺寸的增大而减小,即振动局部化振型可以通过增大嵌入体的尺寸向低频移动.