轮对非线性动力学系统蛇行运动的解析解1)

史禾慕 曾晓辉 ,* 吴 晗

* (中国科学院力学研究所流固耦合系统力学重点实验室,北京 100190)

† (中国科学院大学工程科学学院,北京 100049)

** (大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024)

引言

铁路车辆蛇行动力学响应特性是列车设计和运营中的关键问题,国内外学者对此进行了大量研究.关于整车系统动力学的分析大都采用数值方法.Schupp[1]将基于路径跟踪法的分岔分析软件和Simpack 多体动力仿真软件相结合研究系统的分岔特性,计算了车辆系统的极限环.Cheng 等[2-3]研究了车辆系统的不同参数对于临界速度的影响规律.文献[4-5]等研究了车辆系统的分岔特性,计算了车辆系统的分岔图和极限环等.文献[6]分别采用路径跟随(path-following)方法和蛮力(brute-force)方法研究了铁路客车的分岔和蛇行运动特性.True[7]对于几种求解车辆系统非线性临界速度的方法进行了分析,并给出了求解非线性速度的正确方法.Iwnicki等[8]总结了铁路货车的发展历史,研究了几种常见铁路货车的动力学特性.翟婉明[9]提出了车辆-轨道耦合动力学理论,使得理论研究更能反应铁路轮轨系统实际情况,对于轨道类型对车辆系统的临界速度影响进行了广泛研究.曾京[10]采用QR 算法和黄金分割法计算了17 自由度经典客车模型的线性临界速度,采用打靶法计算了其邻域的极限环.罗仁和曾京[11]的研究表明,在研究列车系统蛇行运动稳定性时,采用单节车模型计算得到的临界速度与多编组列车的临界速度相差很小.高学军等[12-13]采用延续算法计算了车辆系统的周期解,研究了车辆系统的分岔和混沌现象.Zeng 等[14-19]综合考虑了气动载荷对车辆动力学系统固有特性的影响以及强迫激励的作用,给出了气动载荷作用下车辆系统动力学响应特性分析方法,分析了相关参数的影响规律.

上述对整车动力学系统进行研究更接近实际情况,也搞清楚了一些作用机理.尽管如此,目前仍然有一些问题的内在机制不很清楚.部分原因是,整车系统自由度较多、可变参数也多,各参数对蛇行稳定性影响的效应交织在一起,不易分清各种因素的贡献大小,也就不容易更深刻理解为什么会有这样的影响规律.这种状况并不利于高效地改进工程设计.

轮对系统保留了影响车辆系统动力学性能的几个关键的要素:轮轨几何非线性约束、轮轨接触蠕滑关系、悬挂系统等.从蛇行稳定性问题的角度来说,轮对系统也是能从相当程度上代表整车系统蛇行稳定性特性的典型子系统.而且,轮对系统自由度少、参数少,可以采用解析方法进行分析,便于更深入地认识车辆动力响应特性及内在机理.目前国内外学者针对轮对系统也开展了相关研究.

Wagner[20]计算了具有亚临界霍普夫分岔的铁路轮对系统的两个稳定解的吸引域,并给出两个稳定解出现的概率.Casanueva 等[21]建立了考虑轮对柔性的轮对动态稳定性模型,分析了轮对参数对于临界速度的影响规律.Antali 等[22-23]推导了圆锥车轮在圆柱轨道的精确非线性方程,研究了铁路轮对的运动特性.Song 等[24]建立了1/5 轮对比例模型,通过实验和数值研究了车轮踏面锥度对于横向动力学特性的影响.Pascal 和Sany[25]建立了考虑轮轨共形接触的独立轮对动力学模型并研究了其动力学特性.文献[26]研究了具有三次和五次非线性的轮对动力学方程的亚临界霍普夫分岔和鞍结分岔,并通过实验进行了验证.文献[27]研究了轮对系统在两分岔参数下的分岔行为.Ge 等[28]建立了具有非线性等效锥度和轮轨力的修正铁路轮对动力学模型,并对其失稳机理进行了研究.Guo 等[29]建立了考虑轮轨接触非线性的铁路车辆轮对动力学模型,并对其分岔特性进行了研究.武世江等[30]对考虑陀螺效应的轮对系统的霍普夫分岔特性进行了研究,给出了线性临界速度表达式,基于打靶法计算了轮对系统的分岔图.

本文采用解析方法对轮对系统的蛇行运动稳定性问题开展研究.推导出带有小参数的两自由度方程,并采用多尺度方法[31]进行解析求解;给出轮对系统极限环幅值的解析表达式并对其稳定性进行判定;给出了轮对系统非线性临界速度的解析表达式.将所获得的解析解与数值结果进行对比,验证了解析解的正确性.采用得到的解析解进行了参数影响分析.

1 轮对动力学建模

1.1 模型概述

轮对系统是铁路车辆动力学系统中最关键的部分,它包含悬挂系统以及两个通过车轴连在一起的车轮(称为轮对).一系悬挂系统将轮对和转向架构架连接起来;轮对受钢轨约束,在钢轨上无跳跃地运动.轮对系统示意图如图1 所示.

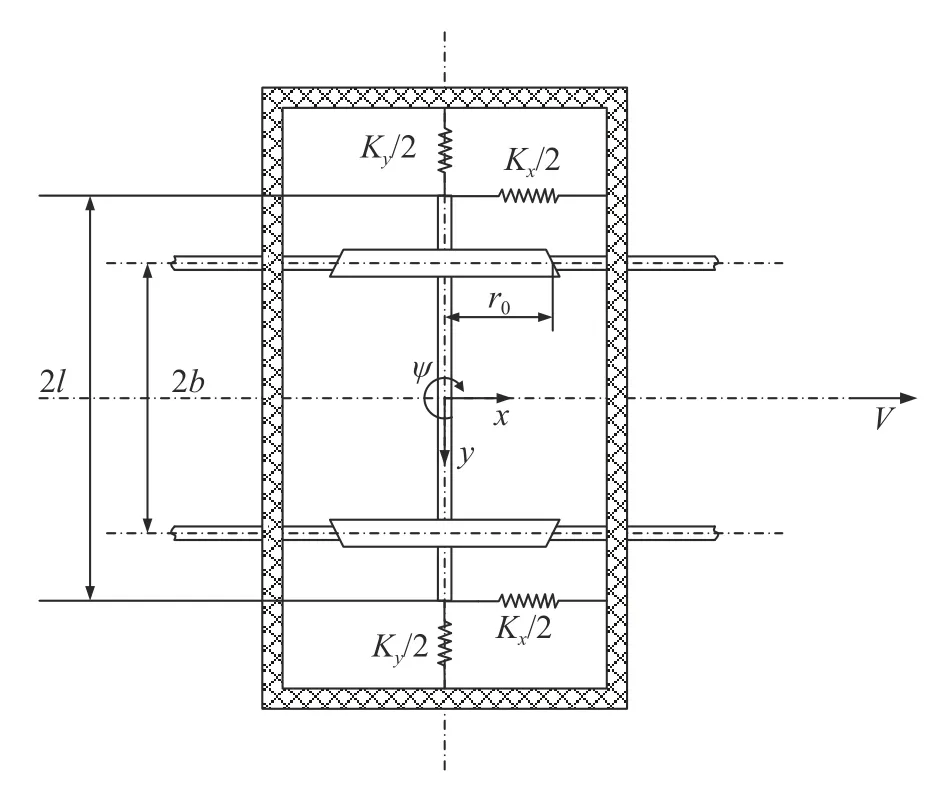
图1 轮对模型示意图Fig.1 Schematic diagram of the wheelset model

在上述轮对系统中,转向架构架沿水平方向匀速前进,轮对沿着轨距不变、刚性路基的平直轨道运动.轮对和构架之间由一系悬挂弹簧连接.车轮与钢轨永保接触,由此轮对的垂向和侧滚位移与其横摆和摇头位移相关联,于是考虑模型有横摆y和摇头ψ两个自由度,车轮和钢轨间的蠕滑符合线性规律,不考虑自旋蠕滑的影响.系统的非线性来自于轮轨接触非线性回复力.

1.2 轮对动力学方程

通过牛顿-欧拉法推导轮对动力学方程如下所示

式中,m是轮对的质量,J是轮对相对于垂直轴的摇头转动惯量,FLx和FLy是左侧车轮的纵向和横向蠕滑力,FRx和FRy是右侧车轮的纵向和横向蠕滑力,Kx和Ky是一系悬挂纵向、横向弹簧总刚度.Fc代表由轴重和轮轨几何关系引起的横向复原力,b是名义滚动圆距离之半,l是一系悬挂横向距离之半.

本文中采用卡尔克(Kalker)线性蠕滑理论计算轮轨接触蠕滑力[20,27-28,30,32-33],如下

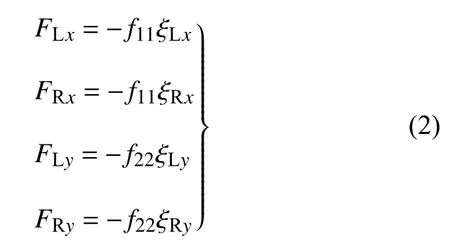
式中,f11和f22是车轮的纵向、横向蠕滑系数,ξLx和ξLy是左侧车轮的纵向、横向蠕滑率,ξRx和ξRy是右侧车轮的纵向、横向蠕滑率,具体表达式如下

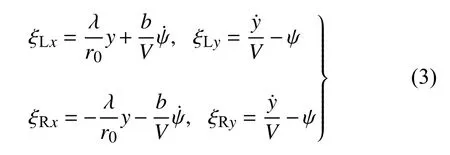
式中,λ是等效锥度,r0是名义滚动圆半径,V是轮对运行速度.

车辆动力学中轮轨接触恢复力通常由轮轨接触几何和轮对轴重决定,表达式如下

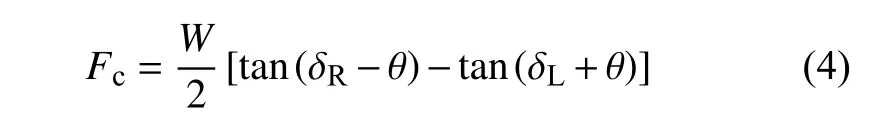
式中,W是轴重,δL和δR是左、右车轮接触角,θ是轮对侧滚角.对于LMA 型车轮踏面和CHN60 型钢轨接触配合,接触几何参数tan(δR-θ)-tan(δL+θ)随轮对横摆的变化关系可用多项式函数拟合,如图2所示.

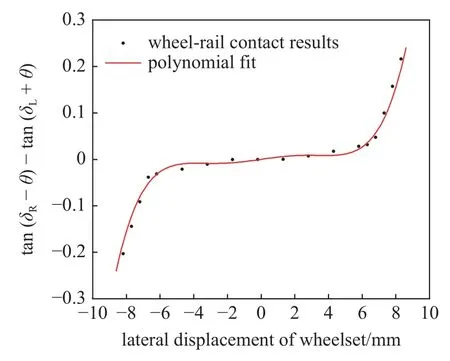
图2 tan(δR-θ)-tan(δL+θ)随轮对横摆变化关系Fig.2 tan(δR-θ)-tan(δL+θ)varies with the lateral displacement of wheelset

具体的拟合公式如下

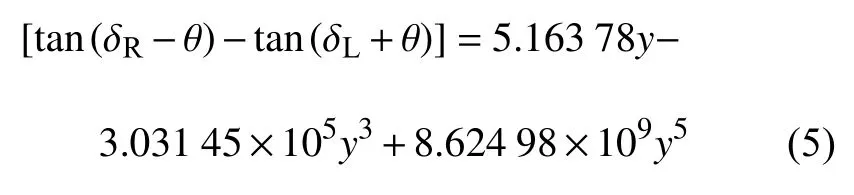
将式(5)代入式(4)有

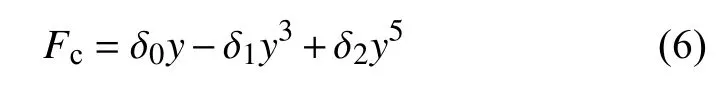
式中δ0,δ1和δ2是关于轮轨接触横向复原力的多项式拟合函数的系数.

将式(2)～式(6)代入式(1),重写轮对动力学表达式如下

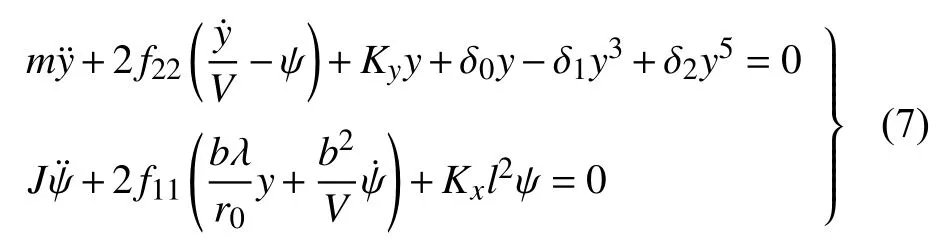
方程(7)中各符号参数的取值参见附录A 中的表A1.

由于方程(7)带有三次和五次非线性,很难得到其精确解,于是考虑采用摄动法求解其近似解析解.

为采用多尺度方法求解如式(7)所示的非线性方程,首先选择合适的特征量对动力学方程进行无量纲化,把式(7)变为带有小参数的无量纲方程,如式(8)所示

式中

对于目前常用的轮轨外形(LMA 型车轮踏面和CHN60 型钢轨)和刚度[20,28]等参数进行计算,式(8)中非线性项的系数ε约0.1,此时无量纲化的动力学方程(8)可以采用多尺度方法进行求解.

2 多尺度法求解轮对动力学方程

本节给出基于多尺度方法的方程(8)的一阶解析解.

设方程(8)的解的形式

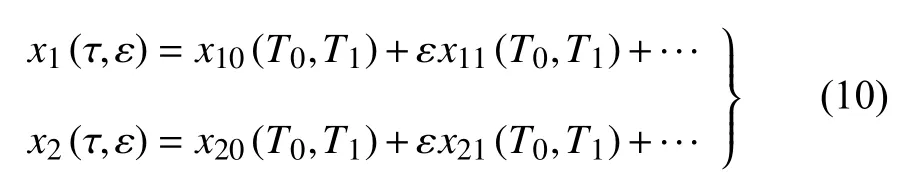
式中Tn=εnτ(n=0,1,2,···),于是对时间的微分可表示为如下形式

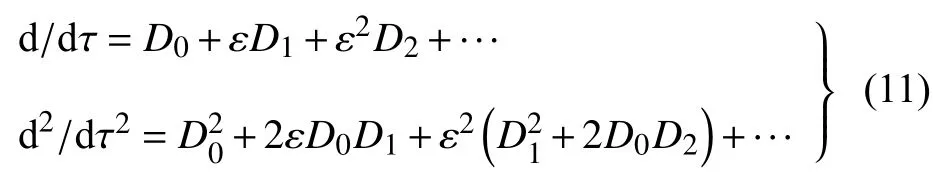
将式(10)和式(11)代入方程(8),并令两端ε0和ε1的系数分别相等,得到

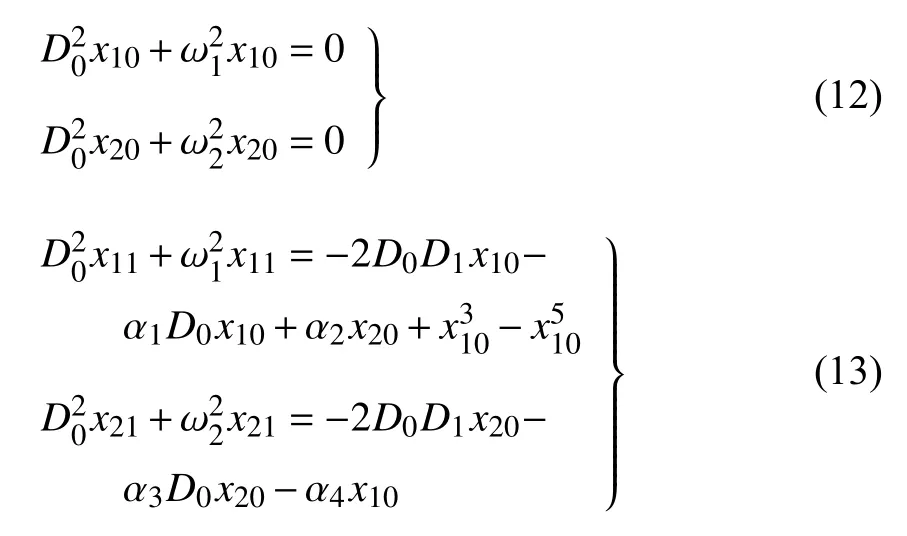
方程(12)的解可写成如下形式

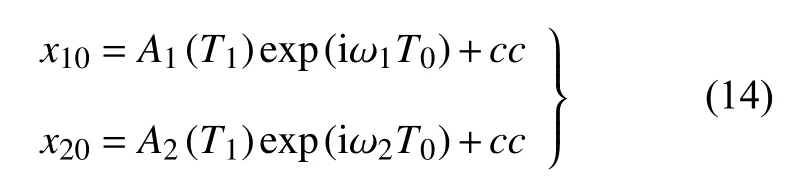
式中An(n=1,2)为待定复函数,cc表示左边各项的共轭复数.

将式(14)代入方程(13)有

式中横线代表该函数的共轭复数.为避免久期项的存在,函数An(n=1,2)需满足以下方程

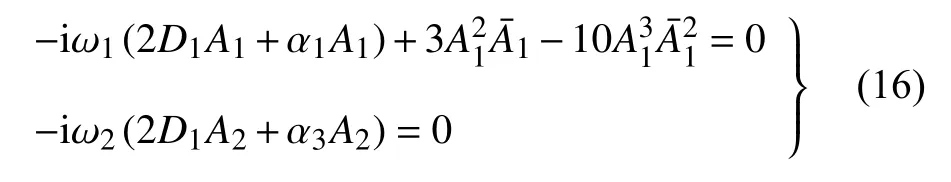
在上式中将An(n=1,2)写成指数形式

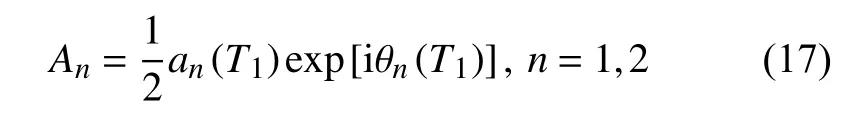
式中an和θn(n=1,2)都是实数,将式(17)代入式(16),并分离实部和虚部,得到

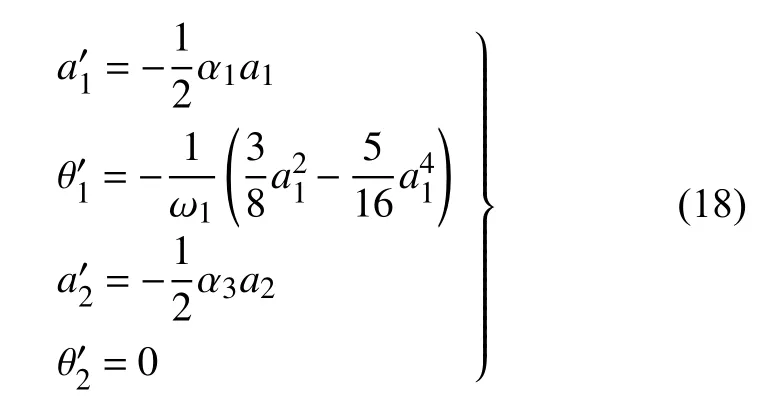
式中,一撇代表对T1求导数.对上式积分可以得到

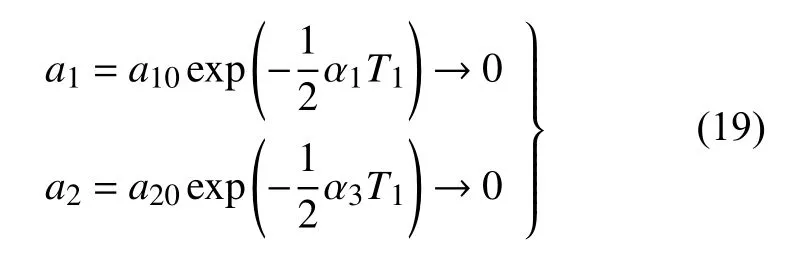
众所周知,铁路轮对动力系统是一个自激振动系统,当运行速度超过临界速度后,系统会出现蛇行失稳导致蛇行运动振幅不再衰减,此时蛇行运动的振幅和频率与运行速度相关.工程实际中,式(19)中参数α1和α3总是正数,因此无论速度如何变化,随着时间的增加,系统蛇行运动幅值a1和a2总是趋近于零.这显然与实际情况不符.实际上在这里需要考虑系统的内共振的影响.由于轮对的蛇行运动是轮对的横摆和摇头相耦合的运动,通过内共振可以将轮对的横摆和摇头运动结合起来,这一点也是符合实际意义的.下面给出考虑内共振时方程的解.

对于系统的内共振情况,引入解谐参数σ1来表示频率ω1和ω2的接近程度，即

将上式代入式(15),为避免久期项的存在,函数An(n=1,2)需满足以下方程

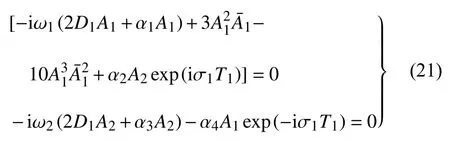
将式(17)代入上式,分离实部和虚部有

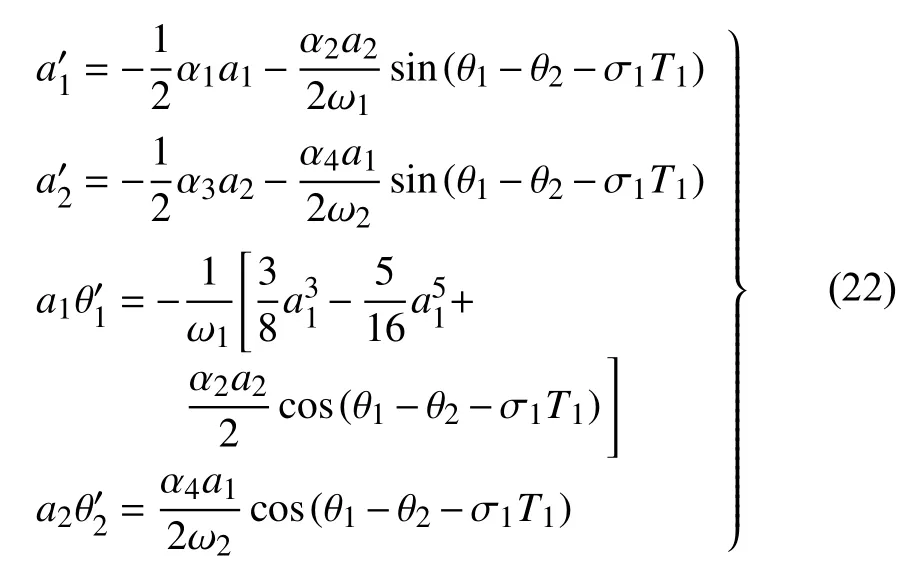
可见,系统总有零解,当系统的幅值(a1,a2)不为零时,引入

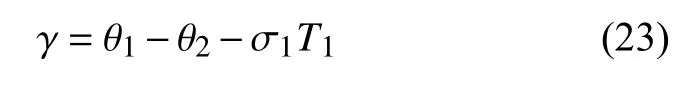
利用上式将式(22)化为自治形式

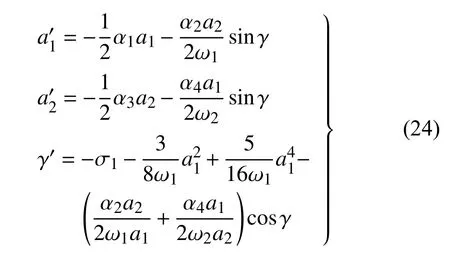
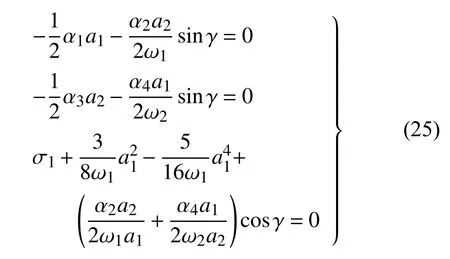
由方程组(25)中前两式可得

在这里考虑稳态幅值均为正,由式(26)可得

将上式代入方程组(25)中第二式有

利用三角恒等式 cos2γ+sin2γ=1,有

将上式和式(27)代入方程组(25)中第三式,化简有

由于 Γ1＜0,需要分情况讨论

(1)Δ±≥0,Γ2±≥0

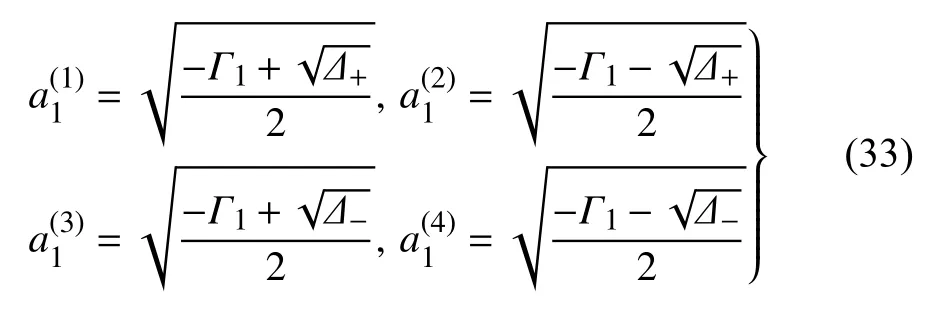
(2)Γ2±＜0

(3)Δ±＜0,系统无非零稳态解,此时系统只有零解.

根据稳态解幅值表达式(33)和式(34)可知,稳态解幅值是随速度变化的函数.Δ±和 Γ2±也是随速度变化的函数,于是不同的运行速度下,系统稳态解的数目可能也不相同.通常情况下,系统的非线性临界速度Vn对应系统发生分岔时的速度,于是,通过求解系统发生分岔时的运行速度来判定系统的Vn.结合式(33)和式(34)可知,此时系统可能有多个分岔点,每一个分岔点对应的速度可能并不相同,即系统在不同的速度下均有可能发生分岔,通常系统发生分岔时的最小速度对应系统的Vn.基于此,下面对系统可能发生分岔的情况逐一讨论.

(1)当 Δ±=0 时,系统发生分岔,此时对应系统的一个分岔速度,称为第一分岔速度

(2)当 Γ2±=0 时,系统发生分岔,此时也对应系统的一个分岔速度,称为第二分岔速度

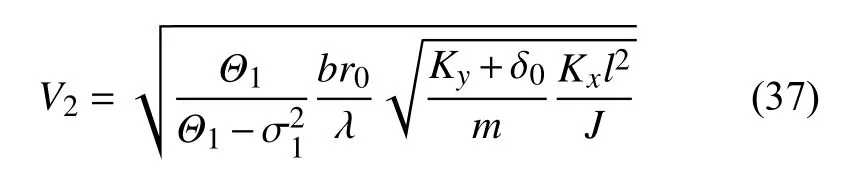
(3)当 Δ+=Δ-,并且系统满足 Δ±＞0 时,此时对应系统的一个分岔速度,称为第三分岔速度

此时系统还需满足

综合上述分析,可判定系统的Vn为

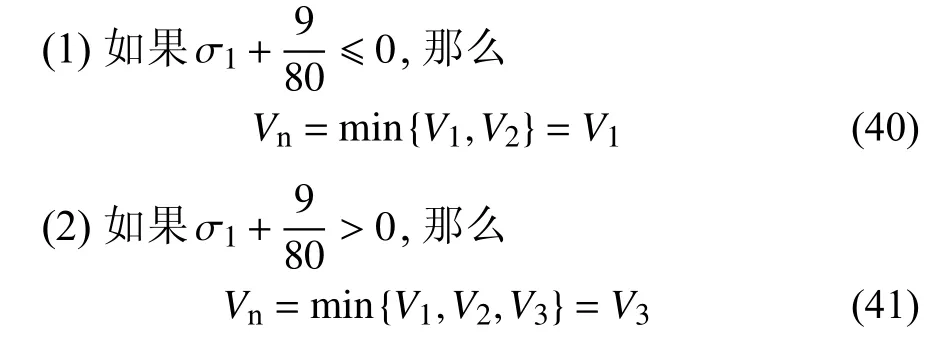
当求得系统稳态幅值a1后,代入式(27)～式(29)可求得a2,γ.对于求得的稳态解稳定性判定,可采用文献[31]中的方法,为此设

式中a10,a20,γ0是系统的一组稳态解,它对应方程组(24)的奇点,即满足式(25).δa1,δa2,δγ是叠加的小的摄动量.将式(42)代入方程组(24),并对δa1,δa2,δγ进行泰勒展开保留一次项,得到

此时系统稳态运动的稳定性依赖于式(43)右端的系数矩阵的特征值,右边系数矩阵如下

式中

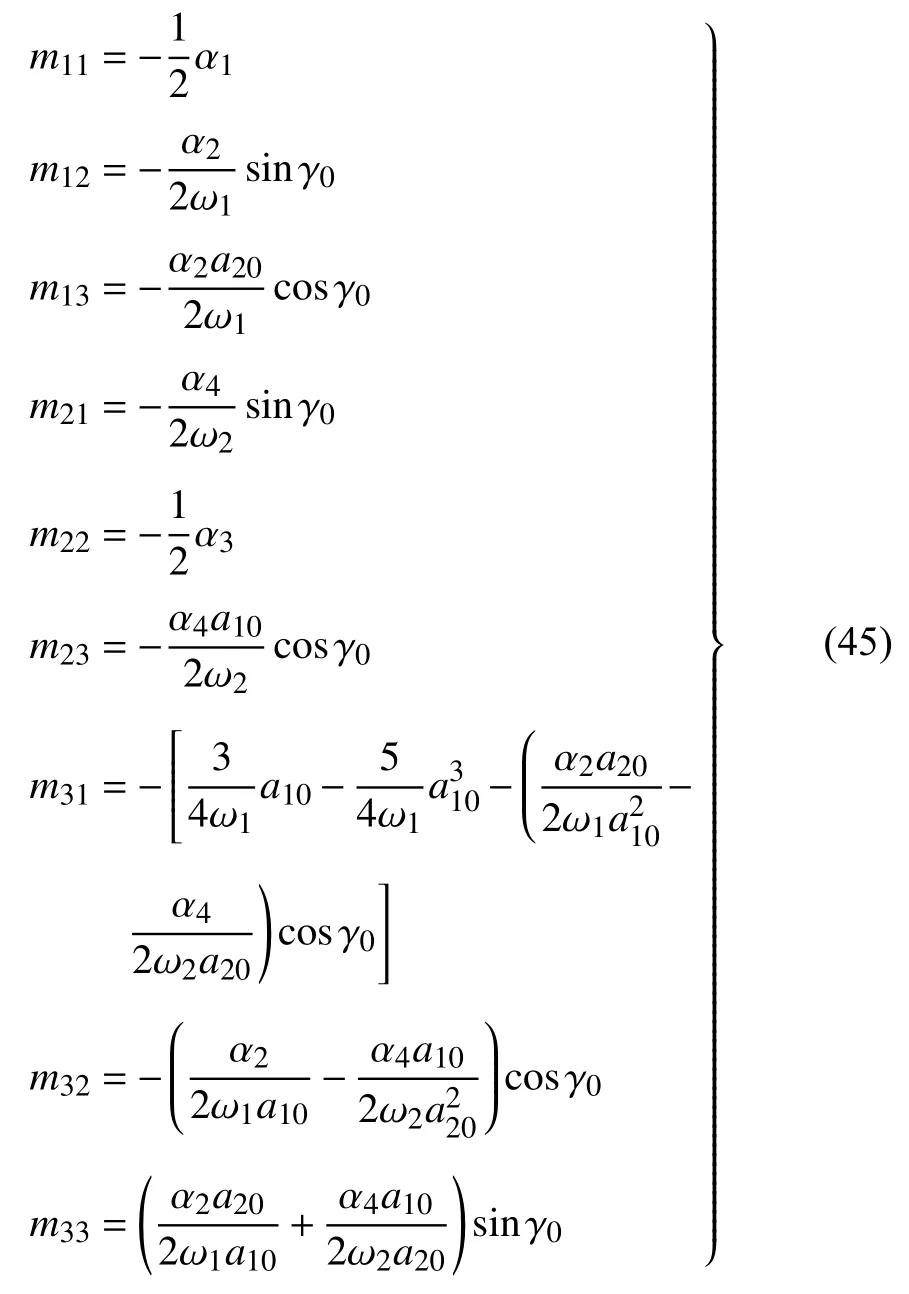
此时特征方程

对上式展开有

式中

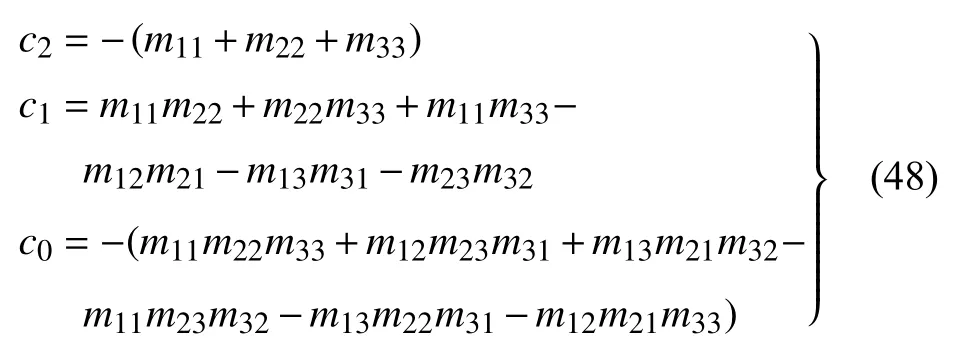
对于方程(47),采用卡尔达诺(Cardano)公式求解如下

式中

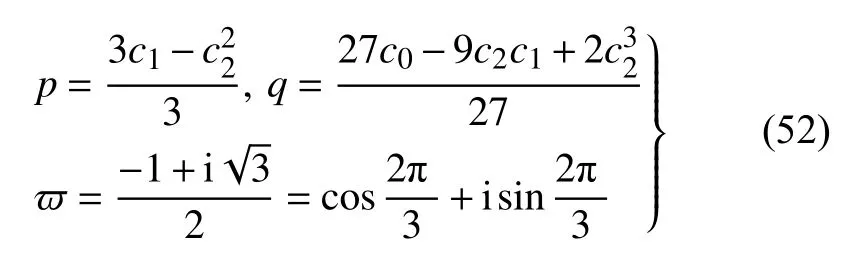
当式(49)～式(51)所对应所有特征值λi(i=1,2,3)的实部均为负数时,对应的稳态运动是稳定的,否则稳态运动不稳定.

将式(14)和式(17)代入式(10),结合式(23),可以得到稳态解的一次近似为

式中，a1,a2,γ均是常数,此时无量纲x1和x2以同一种频率振动,当系统存在稳定的周期解时,系统的蛇行运动频率fh

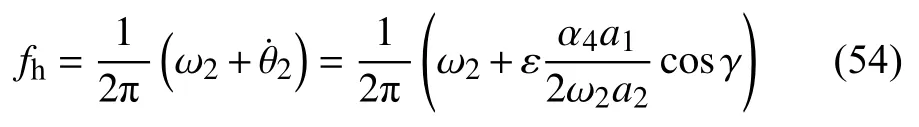
3 结果和讨论

3.1 验证

重新计算文献[20]给出的轮对横摆分岔图的算例,并将本文结果与该文献的结果进行了对比,如图3所示.

图3 中红色三角符号代表文献[20]中轮对横摆幅值结果,蓝色曲线是自编程序的计算结果,二者吻合很好.此外,在之前的研究[14-19]中,将自编程序计算结果和与已有文献中的实验结果和数值结果也进行了许多对比验证.

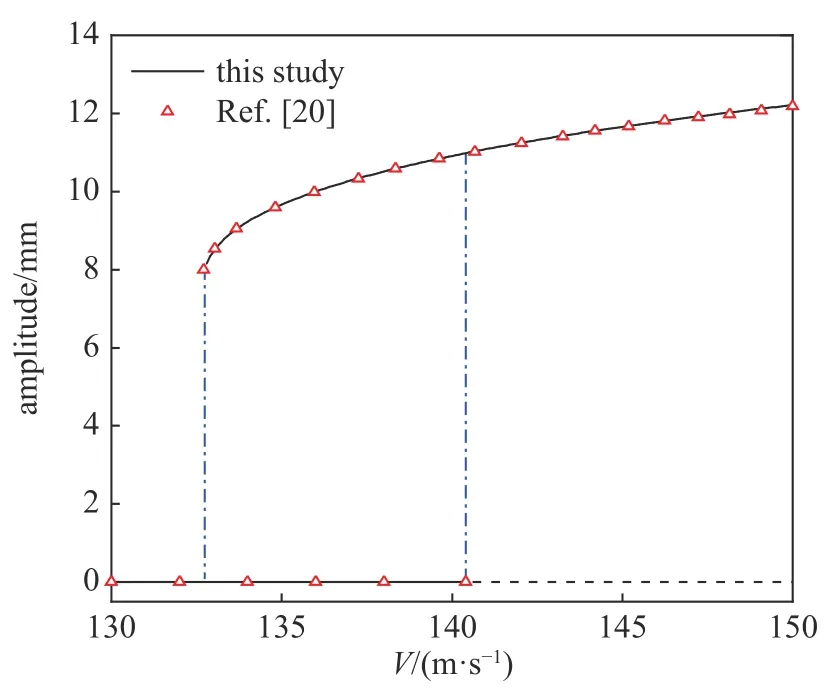
图3 本研究结果与文献[20]结果对比Fig.3 Comparison of results between this paper and Ref.[20]

接下来将数值计算结果和多尺度法的分析结果对比.数值计算采用四阶变步长荣格-库塔(Runge-Kutta,RK)法直接对方程(8)进行数值积分,略去瞬态部分得到x1和x2的时间历程曲线如图4(a)所示,图4(b)是相轨迹在相平面上的投影.

由图4 可知,此时x1和x2作周期运动,对其时间历程曲线进行快速傅里叶变换(FFT)得到x1和x2的频谱图,如图5 所示.

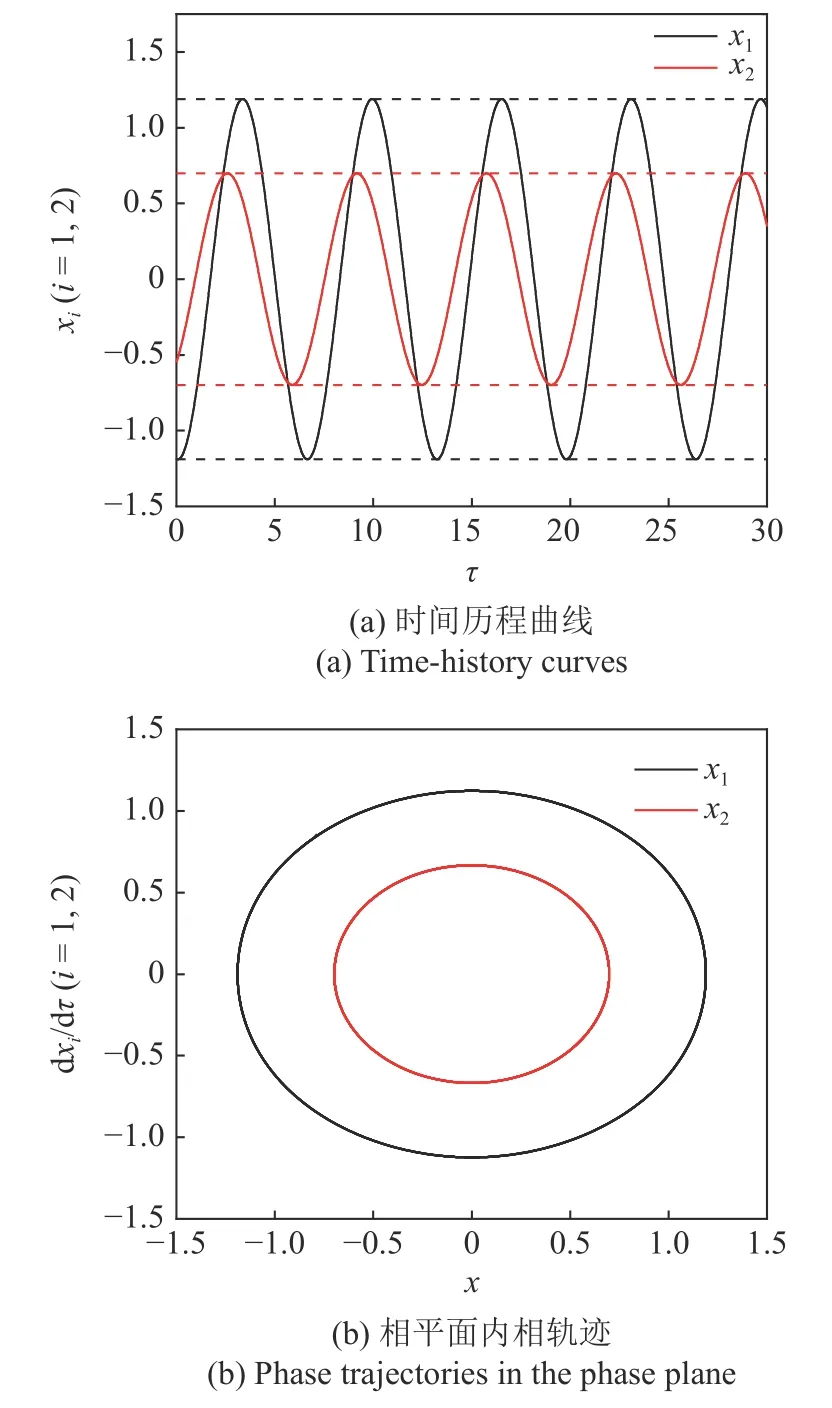
图4 时间历程曲线与相平面内相轨迹Fig.4 Time-history curves and phase trajectories in the phase plane

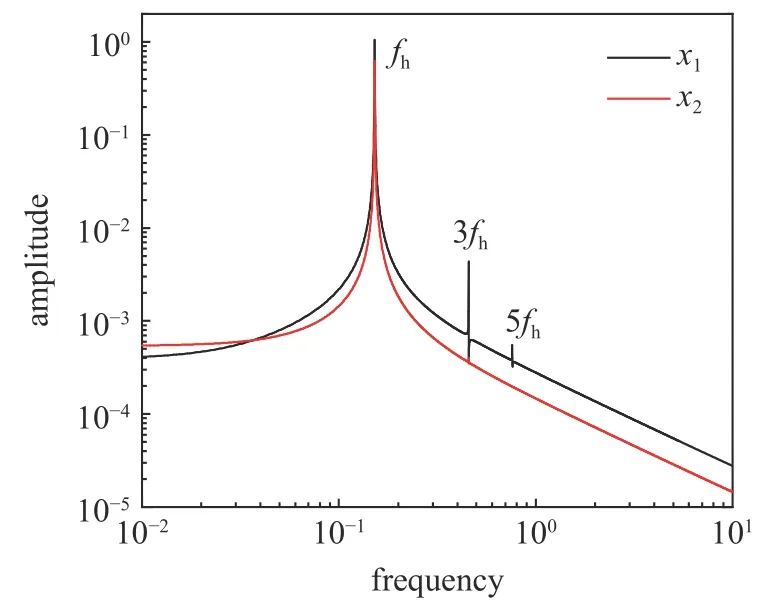
图5 x1 和x2 的频谱图Fig.5 Frequency spectra of x1 and x2

由频谱分析结合图5 可知,此时x1和x2的频率组成由基频fh及fh的奇数倍频组成.fh所对应的谐波分量幅值远大于其他谐波分量幅值.x1和x2以相同的频率fh作周期运动.此时数值计算得到的系统的蛇行运动频率fh为0.152 00,而由本文解析公式(式(54))计算得到的fh为0.151 89,相对误差仅0.07%.我们对x1和x2的时间历程曲线进行滤波处理,得到相应的仅包含基频fh的时间曲线如图6 所示.

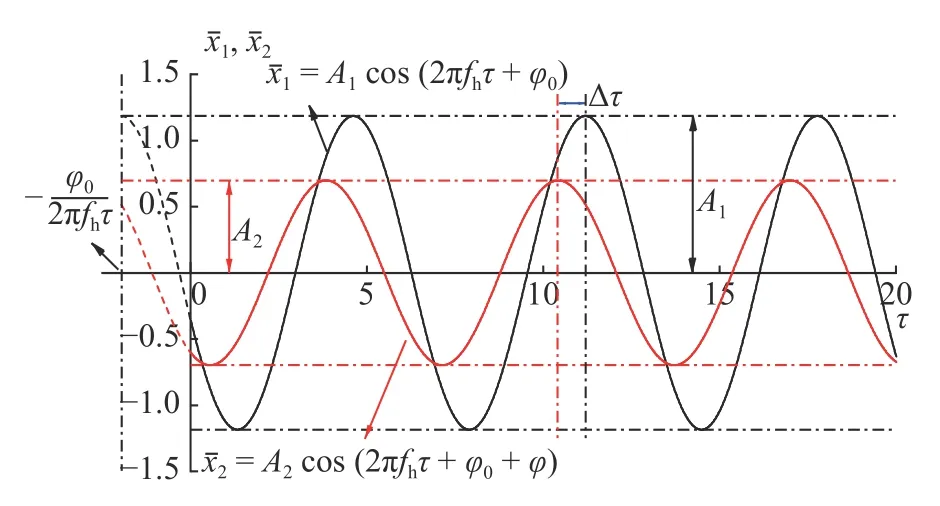
图6 fh 对应的时间历程曲线Fig.6 Time-history curves corresponding to fh

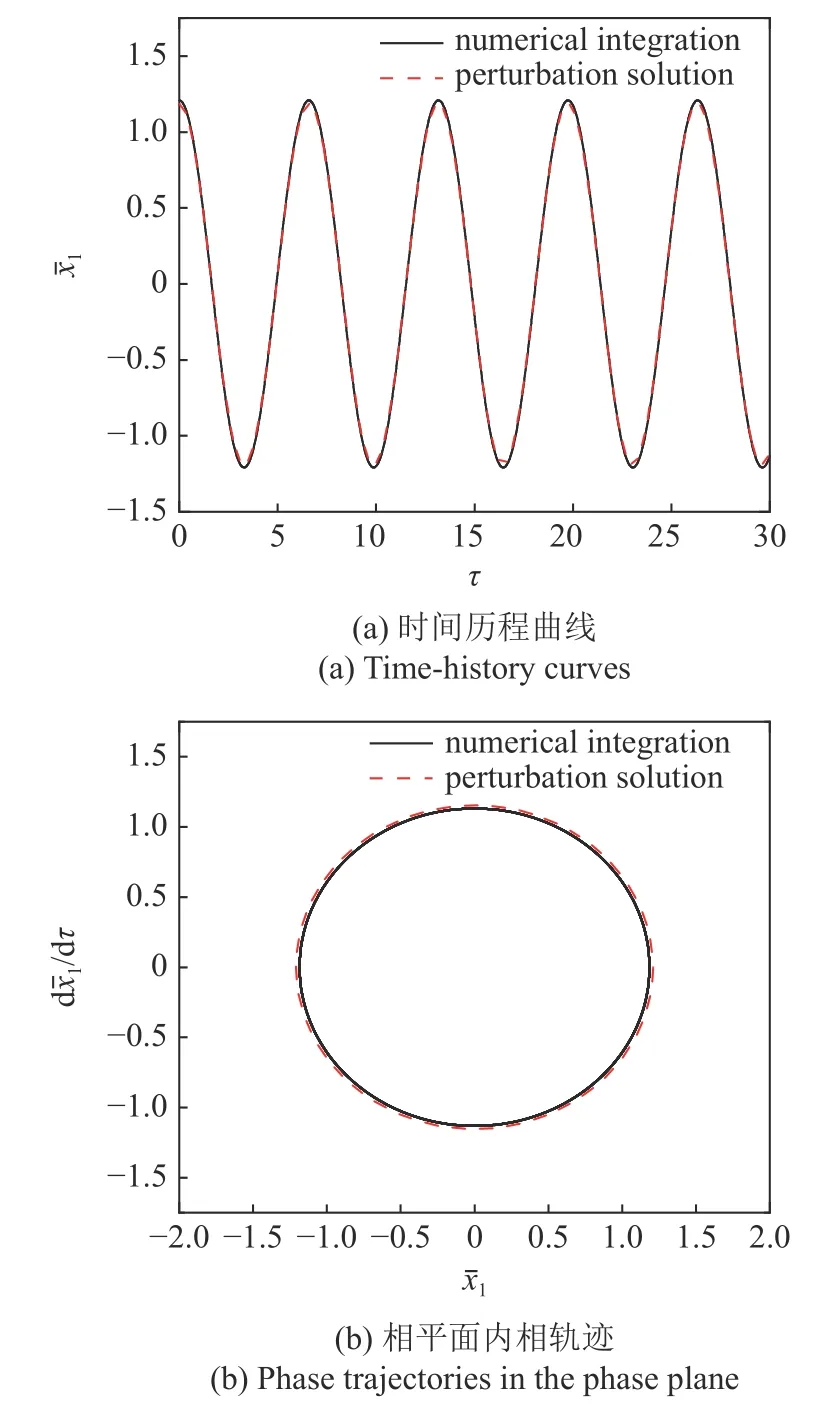
图7 摄动解与数值积分结果对比Fig.7 Comparison between perturbation solution and numerical integration

图8 给出了由本文解析式(27)、式(33)和式(34)计算的轮对横摆和摇头角分岔图和数值结果的对比.图8 中,实线代表稳定的稳态运动的幅值,虚线代表不稳定的稳态运动的幅值,数值积分不能求解出不稳定的稳态周期幅值.结合图8 可以看出,由本文解析解(式(35)～式(38))计算的分岔速度中的线性临界速度Vc约为204.7 m/s,由线性化系统系数矩阵特征值计算的Vc为207.1 m/s,相对误差1.16%.因此,本文推导的解析解也能给出关于线性临界速度的一个很好的近似.由本文解析式(35)～式(41)计算的非线性临界速度Vn约为191.0 m/s,由降速法计算的Vn约为191.2 m/s,相对误差约0.1%.系统的稳定的稳态周期幅值相对误差不超过10%.

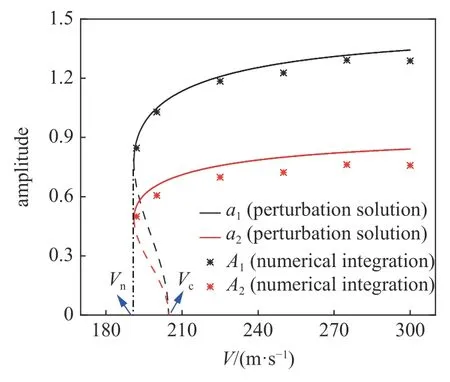
图8 摄动解计算分岔图和数值积分结果对比Fig.8 Comparison of bifurcation diagrams calculated by perturbation solution and numerical integration

通过以上解析公式的计算结果与数值结果的详细对比,我们验证了第2 章中基于多尺度法给出的一阶解析解的正确性.

采用数值法计算轮对系统的非线性临界速度通常需要大量的计算,例如,当采用降速法时:基于路径跟踪策略,首先通过增加运行速度使系统经过扰动后处于稳定的周期运动的状态,即系统有稳定的极限环幅值,随后逐步降低运行速度,在每一步中,当前速度下系统的最终稳态解对应的运动状态作为后续下一个运行速度的初始值从而继续计算,当初值问题的暂态解最终趋于平凡解时,计算结束.此时对应系统的一个分岔速度,通常为非线性临界速度.计算的非线性临界速度的精度取决速度离散化的步长,要获得更加准确的临界速度值,需要细化离散化的步长,导致时间成本增加.而通过非线性临界速度的解析表达式,我们可以直接求解系统的非线性临界速度,更重要的是,我们可以更加方便直接的进行参数对于系统非线性临界速度的影响规律研究.

3.2 参数影响规律

根据非线性临界速度的解析表达式(35)～式(41),很明显,系统的V1,V2,V3与等效锥度λ的平方根成反比,从而系统的非线性临界速度Vn与λ的平方根成反比.图9 给出了由式(35)～式(41)确定的Vn随λ的变化曲线.随着λ的增加,Vn的减小速率逐渐减小.文献[34]中给出,系统的线性临界速度Vc与λ的平方根近似成反比,这说明λ对于Vc和Vn具有相同的影响规律.工程应用中,为提高车辆的运动稳定性,我们应该尽可能提高系统的Vc和Vn.于是在满足其他设计要求的情况下,我们应该尽可能减小车轮踏面的等效锥度.

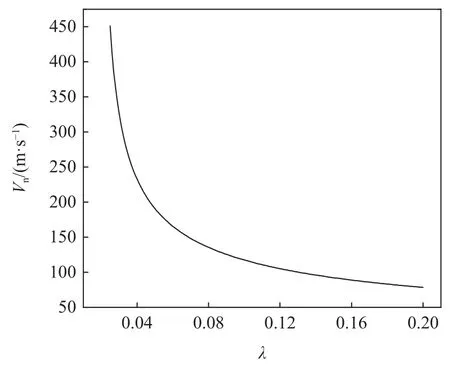
图9 Vn 与λ 的关系曲线Fig.9 Relationship between the Vn with λ

接下来我们研究Vn随一系纵向刚度Kx这一单一因素的变化规律,其他参数保持不变,如图10 所示.

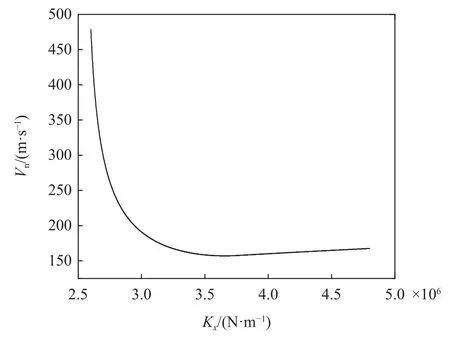
图10 Vn 与Kx 的关系曲线Fig.10 Relationship between the Vn with Kx

当 σ1+=0 时,对应有

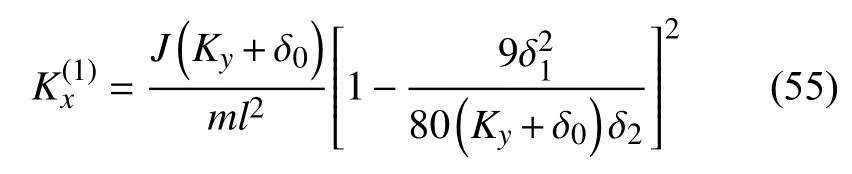
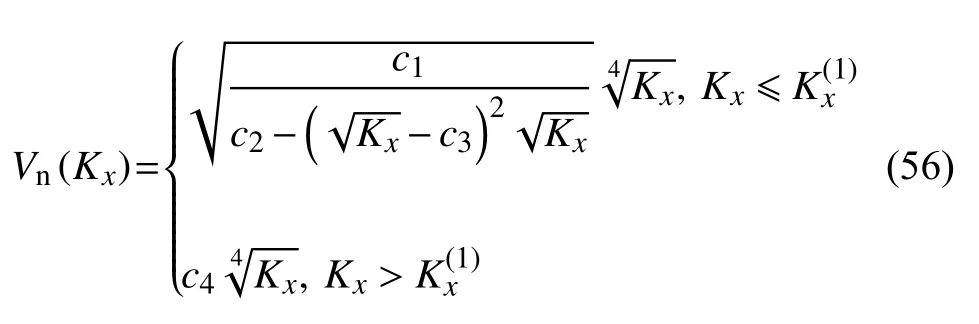
式中c1,c2,c3,c4均是常数.

式(56)中,当Kx＞=3.832 6 MN/m 时,Vn与Kx的四次方根成正比,是随Kx增加而缓慢单调增的函数;而当Kx＜=3.832 6 MN/m 时,从上面表达式可以看出,Kx的四次方根之前的因子不再是常量,而是Kx的非线性函数,因而该式是一个具有极值的函数,我们可以求出其极值.在我们所关注的参数范围内,求Vn解析表达式关于Kx的导数并令其等于零,化简有

图11 和12 给出由本文解析式(27)、式(33)和式(34)计算的无量纲横摆和摇头角分岔图.

图11 中,分别计算了一系纵向刚度Kx取2.9 MN/m,3.0 MN/m 和3.1 MN/m 时系统无量纲横摆和摇头角幅值随速度V的变化曲线.结果表明,同一Kx值对应系统稳定的极限环幅值随着V的增加而逐渐增大,当V越大,极限环幅值的增大速率越慢.同一V值,系统稳定的极限环幅值随着Kx的增大而增大.

图11 不同Kx 值对应系统的分岔图Fig.11 Bifurcation diagram of the system with different Kx

图12 中,分别计算了车轮踏面等效锥度λ取0.04,0.05 和0.06 时系统无量纲横摆和摇头角幅值随速度V的变化曲线.结果表明,同一λ值对应系统稳定的极限环幅值随着V的增加而逐渐增大,当V越大,极限环幅值的增大速率越慢.同一V值,系统稳定的极限环幅值随着λ的增大而增大.

图12 不同λ 值对应系统的分岔图Fig.12 Bifurcation diagram of the system with different λ

一般情况下,根据Vn的表达式(35)～式(41),系统的许多其他参数均会对Vn有所影响,因此在设计转向架参数时,应该对各种不同的参数组合方案进行比较,以期获得最佳的参数匹配范围.本文推导的解析表达式可以对系统参数的初期设计提供一定参考.在进行参数优化设计时,不需要采用数值方法对每一个参数组合进行大量微分方程组的积分计算,采用本文给出的解析表达式(35)～式(41)可以很快计算出每个参数组合对应的动力学性能指标,从而快速获得最优参数组合.

4 结论

本文采用多尺度方法对车辆轮对系统动力学特性进行了解析求解.主要工作和结论如下.

(1)给出了系统的极限环幅值和非线性临界速度的解析表达式.相比于数值解法,通过解析公式,我们可以直接给出系统的非线性临界速度,更加方便地研究系统参数对于非线性临界速度的影响规律.给出了一系纵向悬挂刚度和车轮踏面等效锥度对于系统分岔图和非线性临界速度的影响规律.

(2)在满足其他设计要求的情况下,一系悬挂刚度对临界速度影响较为复杂.在我们所研究的参数范围内,系统非线性临界速度随一系纵向刚度的变化存在一个极小值.在刚度较低(极小值左侧)时,临界速度随刚度减小而有较明显增加,而当刚度较高(极小值右侧)时,临界速度会随刚度增加缓慢增加.适当减小车轮踏面等效锥度有助于提升车辆系统的线性和非线性临界速度,从而提升车辆运动稳定性.车辆系统发生蛇行失稳时的极限环幅值随着一系纵向悬挂刚度和车轮踏面等效锥度的增加而有所增加.

(3)在转向架结构设计与参数优化过程中,通过本文给出的解析表达式,可以很方便地计算出系统不同参数组合下的极限环幅值和非线性临界速度,便于快速比较不同参数组合下的多种方案,从而筛选出最佳的参数匹配关系,为转向架结构设计与参数优化提供参考.

附录

附表 A1 轮对参数Table A1 Wheelset parameters