变转速工况下高速列车轴承转子系统特性分析1)

王宝森 刘永强 张 斌

* (石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

† (石家庄铁道大学交通运输学院，石家庄 050043)

** (南卡罗来纳大学工程与计算机学院,美国哥伦比亚 29208)

引言

随着高速铁路的发展,高速列车的安全、可靠运行越来越受到重视,而轴承作为列车走行部的关键部件,其好坏和运动状态决定了列车的运行质量.国内外的专家学者提出了多种不同的方法来检测列车轴承中是否存在故障,评价轴承的运动状态,其中包括:轴温检测法[1]、声发射缺陷检测方法[2]和用于故障检测、识别和定位的振动信号的信号处理方法[3]等等.然而以上这些方法易受外界干扰,故障检测的准确性也会受到显著影响.

众所周知,存在故障的轴承的振动信号会显示出周期性的峰值[4],这些峰值的频率和幅度与轴承故障的严重程度和位置有关.基于此,快速傅里叶变换FFT 被用于研究快速诊断轴承故障的频谱分析技术[5],并开发了相应的实验室模块[6].然而,故障信号常常被其他信号调制和湮没,极大地影响了这些基于FFT 的方法的准确性.为了提高故障信号提取效率和信号特征分析的准确性,引入了经验模态分解[7]、集成经验模态分解[8]和小波变换[9]等时频域分析技术,以进行信号的预处理和特征提取.例如,基于带宽经验模式分解和自适应多尺度形态分析的故障诊断方法就被应用于轴承的早期故障诊断,并得到了良好的效果[7].随着神经网络技术的发展,基于深度学习的轴承故障诊断技术也蓬勃发展,多种网络模型被应用到了故障诊断和信号处理过程中,其中包括卷积神经网络模型[10]、基于自动编码器的深度神经网络模型[11]和深度信念网络[12].但是这些方法通常应用于常见旋转机械的轴承故障诊断和系统运动状态研究.与常用轴承不同,高速列车轴承常常工作在高速、重载的环境中,且极易受到轴承转子系统内部零件间碰撞产生的冲击信号的调制.传统的信号处理方法难以从这类信号中提取特征,并对轴承系统的运动状态做出准确判断.为了解决这个问题,一种基于模型仿真的方法被提出来并获得不断改进和完善,其基本思想为:利用牛顿第二定律建立一组微分方程组来模拟轴承-转子系统,通过对方程组进行数值求解得到系统响应,从机理角度研究系统的运动状态和故障对系统运动状态的影响.

文献[13]建立了一个具有单点内圈故障的轴承模型,模型由一系列冲击和冲击衰减函数组成,来描述轴承运行过程中滚子通过故障位置时所产生的撞击现象.最后通过振动信号频谱的解调谱验证了模型的有效性.Rafsanjani 等[14]建立了内圈、外圈和滚动体表面存在缺陷的滚动轴承非线性动力学模型,并利用经典的Floquet 定理对模型进行了稳定性分析.陈果[15]建立了航空发动机转子-滚动轴承-机匣耦合动力学模型,并分析了弹性支承刚度、挤压油膜阻尼器等系统参数对系统运动状态的影响.曹青松等[16]针对高速列车滚动轴承内圈与轴径配合面出现松动故障的问题,提出了车体-车架-悬挂-轮轨垂直耦合动力学模型.文献[17]建立了一个包含牵引驱动系统和轴箱轴承的综合的三维车辆-轨道耦合动力学模型,模型考虑了轴箱轴承与其他部件(如轮对和转向架构架)之间的动态相互作用.刘永强等[18]建立了12 自由度含有外圈故障的高速列车轴箱轴承非线性动力学模型,并从非线性动力学角度研究了轴承转速和故障尺寸对系统运动状态的影响.然而,在实际列车运行过程中,轴承的旋转速度是不断发生变化的.上述已有模型的不足之处是它们无法确定变转速工况下轴承滚子的空间位置,因此不能真正模拟高速列车轴承的实际运动状态.Mishra 等[19-20]建立了滚动轴承的键合图模型,用于在不稳定工况下产生振动信号,但是该模型主要是用于故障诊断研究,并不能研究系统参数和系统稳定性之间的关系.此外,大多数现有的模型均是基于非线性动力学来对系统进行状态分析,结果偏向于理论,难以与实际工程应用相结合.更为重要的是,选择合适的参量对高速列车轴承进行可靠性评估是目前亟待解决的问题[21],然而能够描述高速列车轴承在变转速工况下运动状态的指标还很少.针对这些问题,本工作提出了角度迭代法,用来确定滚动体在任意时刻的空间角度,建立了可以在匀速工况和变转速工况下运行的高速列车轴承转子系统动力学模型,以二维不变矩为特征指标对变转速工况下轴承-转子系统稳定性作了定量分析,并进一步研究了在不同转速条件下,转子系统稳定性临界状态对应的轴承最大故障,以期对高速列车轴承安全运行提供实际指导.

1 轴承模型

1.1 轴承转子系统耦合模型建立

1.1.1 转子(车轴)系统模型

该模型为一个轮对包含有一根车轴和两组轴承-转子系统(因为其左右对称,所以这里只讨论其中一组),车轴向外延伸并由轴箱支撑,相当于固定在地面上,简化的轴承转子系统模型如图1 所示.模型保留了轮对各组成部分间的位置和作用力关系,可以模拟轴承-转子系统的运动和作用力规律.本文中接触角α=10°,半锥角β=1.7°.由振动力学[22]知识可知,车轴质量可以等效至车轴中心处,在本文称其为转子.

图1 轴承转子系统模型Fig.1 Model of bearings and rotor coupling system

在转子系统模型中,轴承的支座反力是关键力元,它受滚动体和内、外圈滚道之间的接触力影响.轴承在运行过程中,滚动体的位置不断变化,同时也会引起各滚动体与内外圈滚道间接触力方向和大小的变化.由于轴承运动时轴承内、外圈上的力是通过滚动体传递的,所以支座反力是所有滚动体处接触力的合力.在实际应用中,轴承的运动状态和受力是非常复杂的,为了简化计算,同时不降低模型的准确性,引入以下假设:

(1)外圈固定在刚体上,且转速为0,但是在横向和垂向上考虑有位移变化;

(2)滚动体在滚道上的运动形式是纯滚动,不考虑打滑现象;

(3)滚动体和滚道之间的接触力满足胡克定律.

为了求解轴承的支座反力,首先要确定每一个滚动体的空间角度.双列圆锥滚子轴承的侧视图如图2 所示,N0个滚子均匀分布在内外滚道间,角度间隔为2π/N0,在轴承旋转过程中,第i(i=1,2,···,N0)个滚子在时间t时刻的位置角为

图2 轴承侧视图Fig.2 Side view of the bearing

其中γ(t)是编号为1 的滚动体在时间t内转过的角度,初始角度γ(t0)=0.在第i个滚子处的接触形变量为

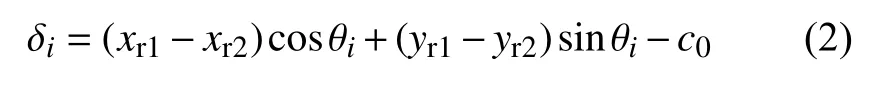
其中,c0是轴承径向间隙;xr1,xr2分别是右侧轴承内圈和外圈的横向位移;yr1,yr2分别是右侧轴承内圈和外圈的垂向位移.根据非线性赫兹接触理论可知,滚动体与滚道之间的接触力为[23]

其中,Kt为接触刚度;在圆锥滚子轴承中,n=10/9;当δi＞0,Hi=1;当δi≤0,Hi=0,此时滚动体与滚道不接触.将每个滚动体处求得的接触力分解到横向和垂向两个方向上,再按方向求和便得到了两个方向上的接触力合力[24],即

其中,FxR,FyR分别为右侧轴承横向和垂向两个方向上的接触力合力.类似地,左侧轴承两个方向上的接触力合力FxL,FyL也可用同样的方式求得.

1.1.2 轴承系统模型

将轴承系统模型视为一系列弹簧-质量模型的耦合模型,则每一部分的位移和速度都可用牛顿第二定律来表示.轴承动力学模型的示意图如图3 所示.轴承在运行过程中,变刚度振动和轮轨激励会导致轴承内外圈、传感器和其他元件产生固有振动,通过调整单元谐振器的刚度和阻尼系数来模拟这些高频振动可以使模型更加准确[25-26].

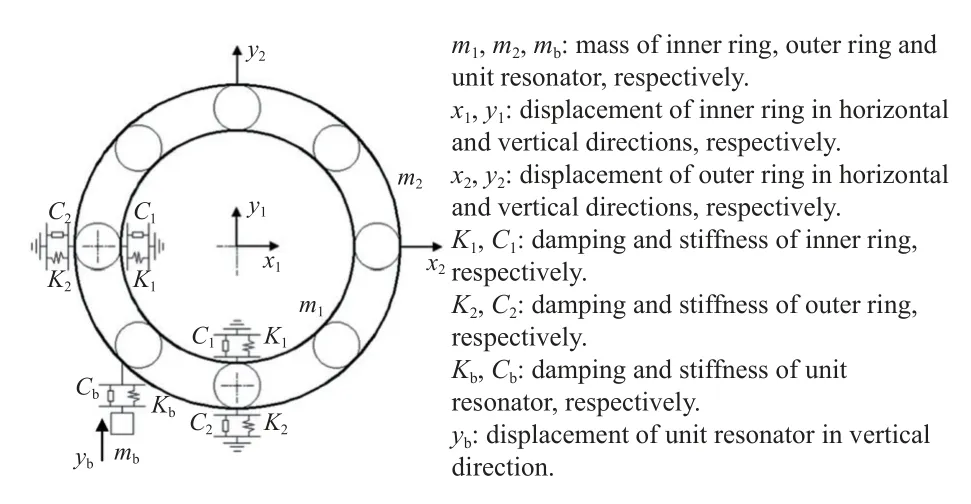
图3 轴承动力学模型Fig.3 Bearing dynamics model

根据牛顿第二定律,轴承转子系统的动力学方程组如式(5)所示

其中,K,C分别为列车车轴的刚度和阻尼;xc,yc分别为车轴中间截面质心的横向和垂向位移;xl1,xl2,yl1,yl2分别是左侧轴承内圈和外圈的横向和垂向位移;yrb,ylb分别为位于右侧和左侧轴承的单元谐振器的垂向位移;F是单个轴承所承载的轴重.在式(5)中,式 Ⅰ 是车轴横向和垂向振动方程;式 Ⅱ 和式 Ⅳ分别为右侧和左侧轴承的横向和垂向振动方程;式Ⅲ 和式 Ⅴ 分别为右侧和左侧单元谐振器振动方程.

1.2 角度迭代法

式(1)中,滚动体转过的角度γ(t)是决定模型是否可以模拟变转速工况下轴承运动状态的关键参数.高速列车在运行过程中,特别是在加速和制动时,其车轴的旋转角速度w0(t)会不断发生变化,所以γ(t)与时间t也非确定的函数关系,为了解决这个问题,确定滚动体在任意时刻的空间角度位置,借鉴文献[19-20]中通过式(6)中的积分求解角度的方法,提出了一种角度迭代的方法,来确定在任意时刻滚动体的空间角度位置,即

角度迭代法假设w0(t)在极短的时间段Δt(Δt→0)内是定值,所以滚动体在t+Δt时间段内转过的角度可以表示为γ(t+Δt)=γ(t)+w(t)Δt,如图2所示.其中,当轴承存在外圈和内圈故障时,w(t)是滚动体和故障区域在时刻t时的相对转速.当滚动体出现故障时,w(t)表示滚动体在时刻t的自转转速.在MATLAB 仿真过程中,Δt代表了ode45 函数在每一次迭代时的步长.基于此,滚动体的空间角度问题转化为不同故障条件下w(t)的求解问题.根据轴承内几何关系可知

其中,d表示滚动体的直径,D表示轴承节径.

2 轴承模型的验证

2.1 系统参数

本文选取了某型号高速动车组的转向架轴箱轴承作为实验对象,其几何参数如表1 所示,轴承系统参数如表2 所示[27],单元谐振器参数如表3 所示.

表1 轴承几何参数Table 1 Geometric parameters of the bearing

表2 轴承系统模型参数Table 2 Parameter of the bearing system model

表3 单元谐振器参数Table 3 The parameter of the unit resonator

2.2 模型的仿真和验证

为了验证模型的有效性,在仿真模型中分别添加了内圈和外圈故障,并得到了模型在定转速和变转速工况下的振动响应.为了进行对比,对外圈故障和内圈故障轴承在相同工况下进行对比实验.由于两种故障类型下得到的结果相似,为了节省篇幅,这里只讨论了轴承存在外圈故障的情况.

在轴承的内圈和外圈滚到位置分别加工了通槽故障,外圈故障宽度Lo=1 mm,内圈故障宽度Lr=0.1 mm.轴承外圈、外圈故障和内圈故障示意图如图4 所示.在轴承实验中,采样时间为10 s,采样频率为51 200 Hz.

图4 轴承外圈、外圈故障和内圈故障示意图Fig.4 The schematic diagram of the outer ring,the outer ring fault and the inner ring fault

加速度传感器安装在轴承轴箱外侧.实验平台和传感器位置如图5 所示.

图5 实验台和传感器安装位置示意图Fig.5 The schematic diagram of the test rig and sensors’ location

2.2.1 匀转速工况

主轴转速(即轴承内圈转速)w0=1600 r/min,轴承外圈故障特征频率为[28]

在该实验条件下,fouter=188.87 Hz.

(1)仿真

轴承外圈仿真振动加速度时域波形和对应的频谱图如图6 所示.

从图6(a)的时域波形中可以看到明显的周期性冲击,这意味着轴承存在有单点故障.而图6(b)的频域曲线中则可发现在外圈故障特征频率及其倍频附近都存在峰值,发现的故障特征频率仿真值与理论计算结果的误差为0.07%,证明了该模型在表达轴承故障特征方面是有效的.

图6 匀速工况下的仿真结果Fig.6 Simulation results under constant speed condition

(2)轴承实验

根据轴承实验结果,轴承外圈振动加速度时域波形和对应的频谱图如图7 所示.受实验过程中背景噪声的影响,在时域波形中虽然无法看到明显周期性冲击信号,但是经过包络谱分析后,在图7(b)中可以找到外圈故障特征频率的基频、2 倍频和4 倍频,其中基频实验结果和理论值的误差为3.7%,证明实验是有效的,也再次证明该模型的有效性.

图7 匀速工况下的实验结果Fig.7 Experimental results under constant speed condition

2.2.2 变转速工况

根据理论计算结果,外圈故障特征阶比为[8,29-30]

根据轴承的几何参数可计算得到fo=7.082.本文使用文献[31] 所述的转速提取方法从实验信号中提取到了相应的瞬时转速曲线,为了使仿真更接近实际,利用小波降噪提取了实验信号中的噪声信号,并添加到了仿真得到的振动信号中.在实验过程中,先将实验台主轴加速到某一转速并保持一段时间,然后逐渐减速到0,信号采样时间为60 s,采样频率为51 200 Hz.

(1)实验

变转速工况下的实验结果如图8 所示.从图8(a)中可以看出,轴承外圈振动加速度的幅值与主轴转速呈正相关.图8(b)中的阶比谱峰值也和理论计算结果吻合,其中基频的误差为5.95%.

图8 变转速工况下的实验结果Fig.8 Experimental results under variable speed condition

(2)仿真

变转速工况下的仿真结果如图9 所示,其中从实验信号中提取得到的瞬时转速曲线作为输入信号应用到仿真中,以保证仿真实验和实际实验在转速上的一致性.从图9(a)中可以看出,其外圈振动加速度的幅值和转速呈正相关.但因为简化后的模型在结构上比真实的轴承简单,参数取值也存在着不可避免的误差,故障引起的冲击不会被其他部件的振动信号调制,故幅值较低.图9(b)中,在故障特征阶比的基频及其倍频处均出现峰值,且仿真结果和理论计算结果几乎相等.仿真结果和实验结果都证明了该模型在变转速工况下的有效性.

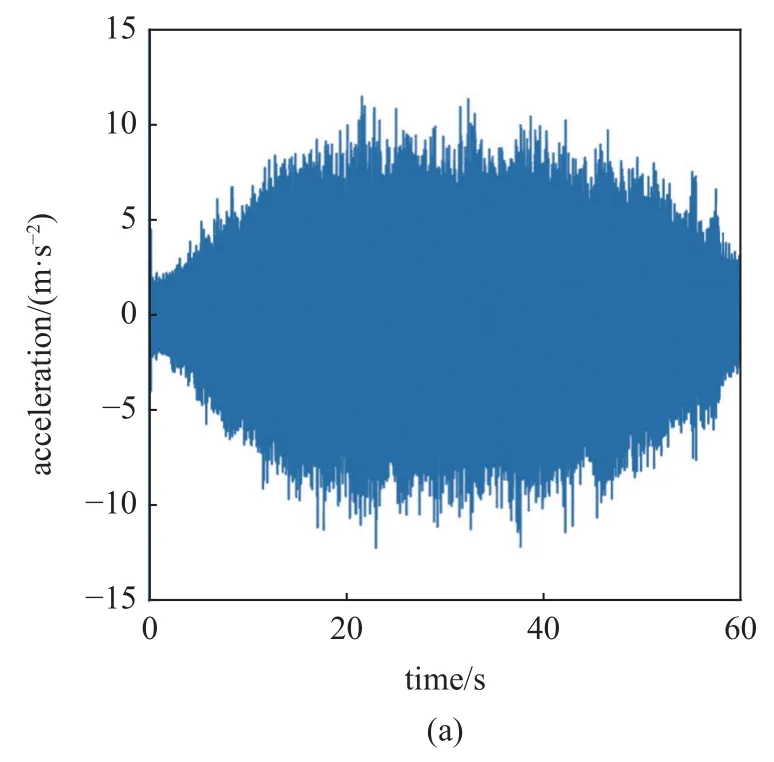
图9 变转速工况下的仿真结果Fig.9 Simulation results under variable speed condition

3 基于轴心轨迹的系统稳定性分析

系统稳定性是指轴承转子系统保持稳定运行状态的能力.在本文中,由轴心轨迹的偏差来表示,偏差越大,系统越不稳定.具有良好稳定性的轴承系统的轴心轨迹会表现得较为集中,轨迹收敛;相反,轴心轨迹会较为发散.将轴承系统振动响应的横向位移和垂向位移分别作为横向和纵向坐标画在同一个图中即可得到轴心轨迹.对于仿真模型,系统位移可直接得到.在实际轴承实验中采集到的信号均为振动加速度信号,将加速度信号经过滤波、降噪、去除异常值、去趋势项和两次积分等处理后便得到了相应的位移信号,就可以绘出外圈轴心轨迹.为了研究外圈故障、内圈故障和滚动体故障对系统稳定性的影响,分别进行了相应的仿真模拟,其中轴承内圈角加速度wac=320 r/min2,故障尺寸L0=1 mm,仿真时间为2 s.对于三种故障类型,转子和右侧轴承内圈(下文的轴承处轴心轨迹表示右侧轴承的内圈轴心轨迹)轴心轨迹如图10 和图11 所示,其中ORF表示外圈故障,IRF 表示内圈故障,REF 表示滚动体故障,下同.

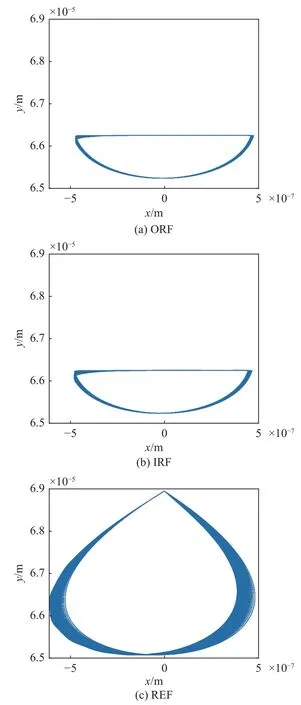
图11 轴承处轴心轨迹Fig.11 Axis trajectory diagram at the bearing

从图10 中可以看出,当轴承存在外圈故障和内圈故障时,轴心轨迹在仿真时间内会收敛到一个集中区域,为了评价收敛速度对于稳定性的影响,将轴心轨迹第一次重合的时刻定义为“收敛节点”,利用MATLAB 绘制动态图的功能,在轴心轨迹重合时刻进行标记来确定“收敛节点”对应的时刻.由此可知,外圈故障的“收敛节点”为0.53 s,内圈故障为0.50 s.“收敛节点”对应的时间越短,系统就越稳定,所以内圈故障对系统稳定性影响较小.当轴承存在滚动体故障时,其转子处轴心轨迹没有明显的收敛规律,且轨迹半径变化幅度很大,说明滚动体故障对系统稳定性有较大程度的影响,对轴承的运行有较大的安全隐患.

图10 转子处轴心轨迹Fig.10 Axis trajectory diagram at the rotor

由于轴承系统比转子系统结构更为紧凑,故稳定性也较好,其轴心轨迹比较稳定,“收敛节点”的值极小.然而当轴承存在滚动体故障时,其轴心轨迹的运动范围和振动位移均比轴承存在其他两种故障时要大,使得滚动体故障对系统稳定性的影响也较大.总的来说,滚动体故障对列车安全运行的影响最大,在实际对轴承故障检测和维护时应该给予滚动体更多关注.

4 基于二维不变矩的系统稳定性定量分析

虽然轴心轨迹可以在一定程度上评价系统的稳定性,但是这种影响并不直观,更多的是定性评价.为了定量比较轴承滚动体故障对系统运动稳定性的影响,采用二维不变矩作为特征指标.1962 年,Hu[32]提出了平面几何图形的二维不变性理论,并提出了7 个几何矩的不变量(前两个分别评价图形的集中程度和对称度,故本文只应用前两个).利用二维不变矩进行图像分类和识别的方法[33]现已成熟地应用到了工业图像中无损检测、人脸特征提取[34]和医学领域的病变细胞的自动识别等领域.

密度分布函数ρ(x,y)的(p+q)阶矩用黎曼积分定义为

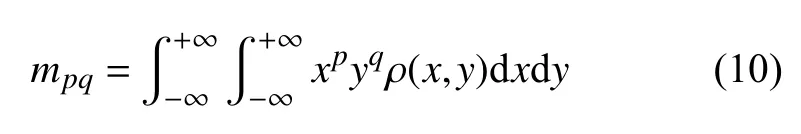
图像的0 阶矩表示图像的质量

图像的一阶矩可以用来确定图像的质心

将图像的坐标原点平移至(xc,yc)处,即得到对于图像位移不变的中心矩

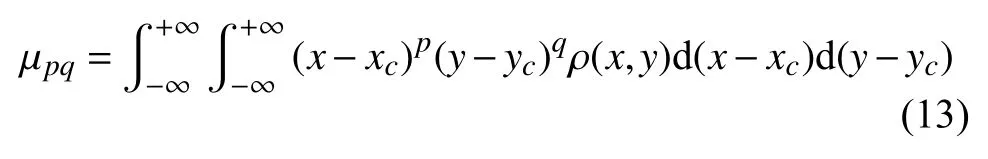
对μpq归一化处理,保证中心矩对尺度变化的恒定

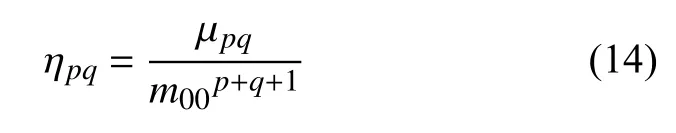
依据此给出Hu[32]提出的前两个不变矩,其特征可以对图像的位移、尺度和旋转变换保持恒定

由于不变矩在图形发生尺度、位移和旋转变化时都保持恒定,故可以将其应用到故障轴承转子系统的轴心轨迹定量评价中,以此来判断轴承转子系统的运动稳定性.φ1可以用来评价轴心轨迹的离散程度,φ1越大,表示越发散,系统稳定性就越差.φ2可以用来评价轴心轨迹的对称性,φ2越大,表示对称性越差,系统稳定性就越差.

4.1 匀速工况下的系统稳定性分析

为了使分析结果更有说服力,在实验条件允许的情况下进行了定转速工况下的对比实验.多次重复2.2.1 中的实验,通常情况下,高速列车在运行过程中,轴承内圈的转速相对较高,为了和实际情况保持一致,设置仿真和实验的主轴转速在1200 r/min和2100 r/min 之间.分别进行4 组实验,其中实验台主轴转速分别为1200,1500,1800,2100 r/min,外圈故障尺寸为1 mm,内圈故障尺寸为0.1 mm.在外圈故障和内圈故障条件下的对比结果如图12 和图13所示.

图13 内圈故障条件下对比结果Fig.13 Results comparison under the condition of inner ring fault

从图12 中可以看出,实验结果明显大于仿真结果,这是因为实际实验中的背景噪声导致轴心轨迹的图形发生变形和偏移,使图形的发散程度和不对称程度变大,进而使φ1和φ2的值偏大.总的来说,当轴承存在外圈故障时,系统稳定性会随着转速的升高而变差,所以在列车实际运行过程中,如果轴承产生外圈故障,降低转速是保持系统运动稳定性和避免严重事故的有效手段.

图12 外圈故障条件下对比结果Fig.12 Results comparison under the condition of outer ring fault

与外圈故障不同的是,内圈故障在转速为1800 r/min 时的值均比2100 r/min 时的值更大,说明内圈存在故障时,转速越高系统稳定性越好,这是因为内圈存在故障时,故障所处的方位会随着轴承旋转而不断改变,转速越高,故障产生的振动冲击在圆周方向上分布越密集,使此时轴心轨迹的发散程度和不对称程度降低,从而使φ1和φ2的值降低.所以在列车运行过程中,如果轴承产生内圈故障,在不考虑其他因素的前提下,适当提高转速会有助于提高系统稳定性.

4.2 变转速工况下的系统稳定性分析

高速列车在运行过程中速度经常会发生变化,其轴承转子系统的运动状态也不同于列车匀速行驶的情况,因此有必要对轴承转子系统的稳定性进行分析.分别在外圈故障、内圈故障和滚动体故障条件下进行仿真,轴承内圈的角加速度从0 变化至500 r/min2,分别求得在轴承处和转子处φ1和φ2的值.轴承处φ1和φ2的值与角加速度的关系如图14 所示,转子处φ1和φ2的值与角加速度的关系如图15 所示.在接下来的讨论中,为了解释方便,定义φ1,type,location和φ2,type,location为不同故障条件下不同位置轴心轨迹的φ1和φ2的值,其中type={ORF,IRF,REF},location={rotor,bearing}.例如φ1,bearing表示在轴承处轴心轨迹的φ1的值,φ2,IRF,rotor表示在内圈故障条件下转子处轴心轨迹的φ2的值.

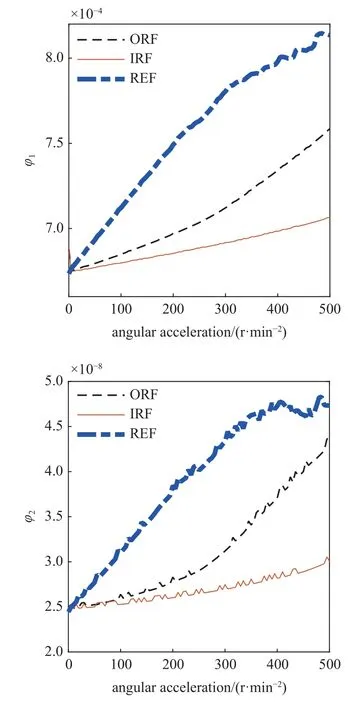
图14 轴承处轴心轨迹的φ1 和φ2 的值Fig.14 Values of φ1 and φ2 of axis trajectory at bearing

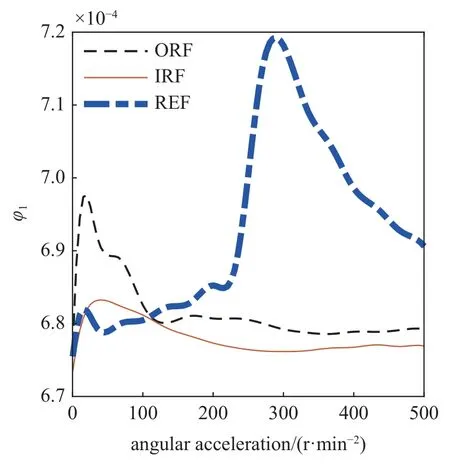
图15 转子处轴心轨迹的φ1 和φ2 的值Fig.15 Values of φ1 and φ2 of axis trajectory at rotor

图15 转子处轴心轨迹的φ1 和φ2 的值(续)Fig.15 Values of φ1 and φ2 of axis trajectory at rotor (continued)

从图14 中可以看出,φ1,bearing和φ2,bearing都随着角加速度的变大而变大,这是因为车轴加速度的增加很大程度上影响了三种故障类型时轴心轨迹的发散程度和不对称程度.由此可知,在加速阶段,列车的加速度越大,其轴承系统的稳定性就越差.同时,当轴承存在滚动体故障时,φ1和φ2的值都是最大的,说明滚动体故障在加速阶段对轴承系统的稳定性影响是最大的.根据轴承故障模型可知,当轴承存在外圈故障时,轴承处轴心轨迹周期性地受到来自同一方向的振动冲击的影响,单向冲击示意图如图16(a)所示,其轨迹的发散程度和不对称程度都有所增加,因而导致其对应的φ1和φ2的值均比内圈故障条件下的要大,所以在加速阶段,外圈故障对轴承系统稳定性的影响比内圈故障更大.

图16 三种角加速度下转子处轴心轨迹Fig.16 Axis trajectory at rotor under the conditions of three angular accelerations

在转子处,三种故障类型对系统稳定性的影响较为复杂.外圈故障、内圈故障和滚动体故障对应的φ1和φ2的值随角加速度变化的曲线均产生了交点.对于φ1而言,其对应角加速度约为120 r/min2,当车轴角加速度小于这个值时,φ1,ORF,rotor和φ1,IRF,rotor都大于φ1,REF,rotor,当车轴角加速度大于这个值时,φ1,ORF,rotor和φ1,IRF,rotor都小于φ1,REF,rotor.这表明,在低角加速度工况下,外圈故障和内圈故障对系统稳定性的影响较大,而在较高角加速度工况下,滚动体故障对系统稳定性的影响较大,但是这种影响随着角加速度的升高,先增大而后逐渐减小.原因是轴承存在滚动体故障时,轴心轨迹更加扭曲,所以φ1和φ2的值较高,而随着角加速度的升高,轴心轨迹逐渐收敛至同一区域,形状不再发生更大变化,表现为φ1和φ2的值逐渐下降且趋于平稳.对于φ2而言,其交点对应的角加速度大约为200 r/min2,也可以得到相似的结论.

为了进一步解释这个现象,选取了三种角加速度的工况(wac=3,100,300 r/min2),绘制了在不同故障条件下转子处轴心轨迹,如图16 所示.为了避免因仿真时间太短导致的误差,将每一种工况的仿真时间延长至10 s.

从图16 中可以看出,当角加速度较小时(3 r/min2),轴承外圈故障会使转子受到同一方向周期性的冲击,即单向冲击,导致转子处轴心轨迹在同一位置产生一个尖峰,集中程度和对称性都受到了一定程度的影响,所以对应的φ1和φ2的值会较大.相反,轴承存在内圈故障和滚动体故障时,轴心轨迹会快速收敛,所以对应的φ1和φ2的值会较小,表明此时转子系统的稳定性较好.因此,在该条件下,外圈故障对转子系统稳定性的影响较大.

随着角加速度的增大(100 r/min2),因故障引起的单向冲击对轴心轨迹的影响程度逐渐降低.轴承存在外圈故障和内圈故障时,轴心轨迹快速收敛至稳定区域,其对应的φ1和φ2的值也比较小.但是当轴承存在滚动体故障时,轴心轨迹变得不规则,明显偏离椭圆形状,发散程度和不对称度更高,其对应的φ1和φ2的值也比较大.因此在该工况下,滚动体故障对转子系统稳定性的影响较大.

在角加速度保持在一个较高水平时(300 r/min2),三种故障类型时的轴心轨迹都快速收敛至各自的稳定区域内,形状也趋于统一,这使得轴心轨迹所对应的φ1和φ2的值偏差变小,如图15 所示.然而,当轴承存在滚动体故障时,其轴心轨迹更为发散,其收敛区域的对称程度较低,所以其对应的φ1和φ2的值依然较大.因此在该条件下,滚动体故障对转子系统稳定性的影响是最大的.

5 稳定性临界状态分析

高速列车在运行过程中,轴承转子系统可能会发生故障,导致其不能按照原来的速度继续行驶,甚至停车.所以,确定列车在保持某一速度时所能允许的轴承最大故障尺寸具有较强的实际工程意义.本节重点讨论在各个速度条件下,轴承所能允许的最大故障,即系统的稳定性临界状态所对应的故障尺寸.由于轴承结构紧密,系统稳定性较好,所以重点研究转子系统,即车轴的稳定性临界状态.定义车轴的稳定性临界状态为车轴质心轨迹对应二维不变矩的值最后一次和无故障条件下的值相等或接近时的状态.根据之前章节的分析也可以看出,φ1和φ2的变化规律也类似,故本章仅以φ1为特征指标.

设置仿真工况为w0(t)=100,600,1100,1600,2100 r/min,分别对应列车运行速度 16.59,99.53,182.46,265.40,348.34 km/h.故障尺寸为0～3 mm,步长为0.037 5 mm.以外圈故障为例,得到了φ1,ORF,rotor的变化规律,如图17 所示.

其中,在转速为2100 r/min 时,有两个临界状态,基于实际工程要求,在轴承转速较大时,必然要求轴承故障尺寸越小越好,故取较小者.从图17 中可以看出,总体上,轴承转速越大,其稳定性临界状态对应的最大故障尺寸越小.这是符合实际情况的.因为随着轴承转速的提高,轴承故障对系统的影响也会越来越大.但是这种影响机制是复杂且非线性的,在某些转速条件下(如1600 r/min),故障尺寸的值不符合速度越高对应故障尺寸越小这种规律.

按照同样的方法分别计算了轴承存在内圈故障和滚动体故障时稳定性临界状态对应的最大故障尺寸,如表4 所示.

从图17 和表4 中可以看出轴承转速在较高水平时,轴承所能允许的最大故障尺寸都比较小.在同一转速条件下,外圈故障尺寸大都是最大的,而滚动体故障尺寸大都是最小的.在变转速条件下外圈故障对转子系统稳定性的影响也体现在了匀速工况下,在转速较低时,稳定性临界状态对应的最大外圈故障也比较小.由此可得出结论,当列车运行速度较小时,对轴承外圈故障尺寸的要求相对比较苛刻,原因是此时外圈故障对系统稳定性影响较大.当列车运行速度较大时,稳定性临界状态所对应的滚动体故障尺寸最小,也从侧面证明滚动体对系统稳定性影响最大.

表4 不同转速条件下稳定性临界状态对应的最大故障尺寸Table 4 Maximum fault size corresponding to stability critical state under different speed conditions

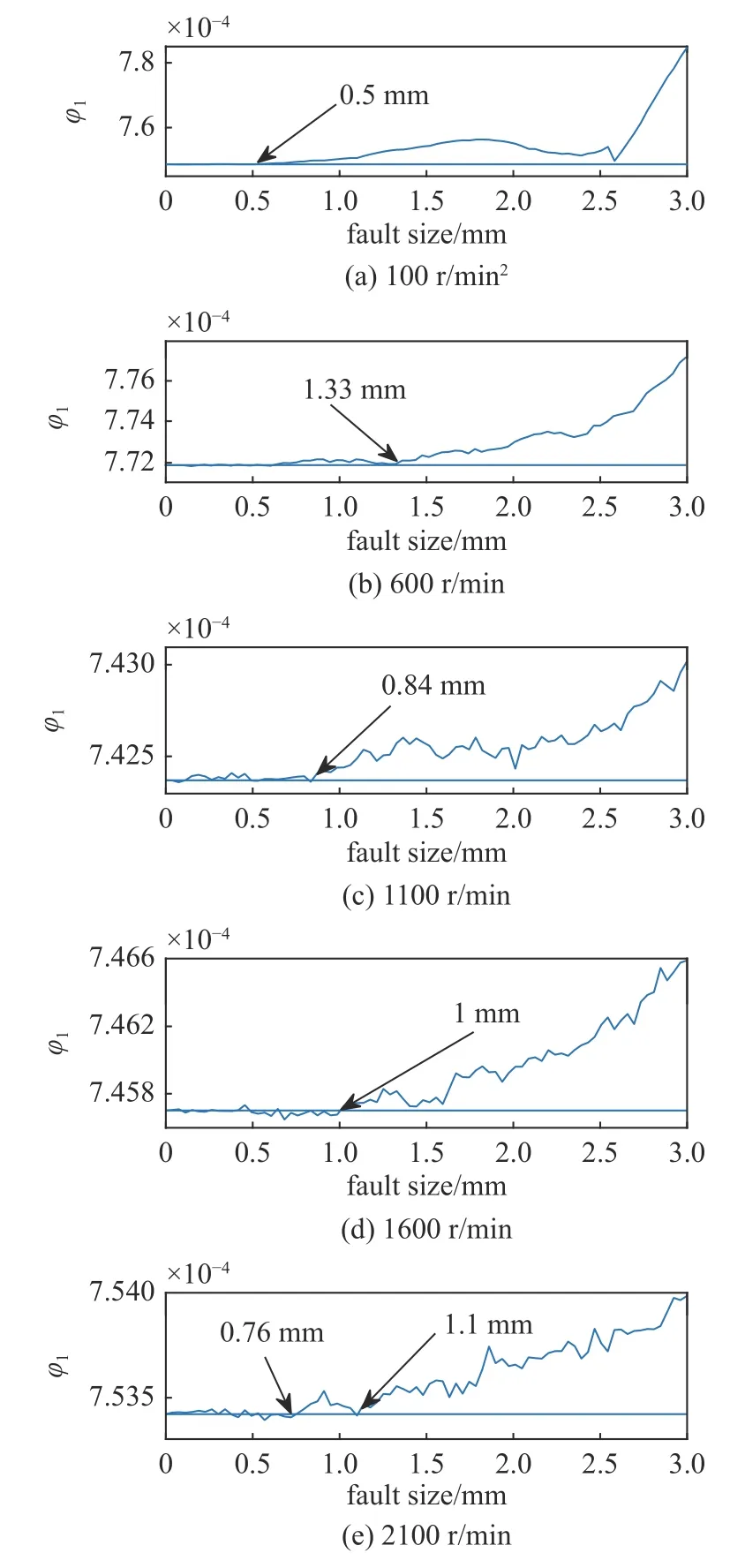
图17 不同转速条件下φ1,ORF,rotor 随故障尺寸的变化规律Fig.17 Variation of φ1,ORF,rotor with fault size at different rotating speeds

6 结论

(1)提出了一种高速列车轴承转子系统动力学模型,模型通过角度迭代法确定了滚动体在任意时刻的空间角度位置.利用MATLAB 计算得到了模型在匀速工况和变转速工况下的振动响应.通过相应的实际轴承实验,验证了模型在两种工况下的有效性.

(2)利用轴心轨迹分析了外圈故障、内圈故障和滚动体故障对轴承转子系统稳定性的影响.并通过相应的轴承实验进行了验证.

(3)利用二维不变矩对定量分析了外圈故障、内圈故障和滚动体故障对轴承转子系统稳定性的影响.分析结果表明,在车轴角加速度较小时,外圈故障对系统稳定性的影响较大,而车轴角加速度较高时,滚动体对系统稳定性影响较大.

(4)研究了不同轴承不同转速条件下,转子系统稳定性临界状态对应的最大故障尺寸.研究结果表明,轴承转速较低和较高时,所对应的滚动体故障尺寸较小.