基于优化多核极限学习机的车轮多边形磨耗识别1)

谢 博 陈是扦 徐明坤 杨云帆 王开云 ,

* (西南交通大学牵引动力国家重点实验室,成都 610031)

† (兰州交通大学机电工程学院,兰州 730070)

引言

随着列车向高速、重载方向的飞速发展,轮轨之间的相互动力作用逐步加强,车轮多边形磨损也日趋严重[1-2].随着运营里程增加会导致多边形车轮磨耗的逐步恶化,不仅造成车辆异常振动,行车稳定性和安全性也会受到威胁,通过车载设备准确识别多边形车轮具有重要意义[3-4].

目前,有学者在多边形车轮的形成机理和磨耗特征上取得了一定研究成果,但对于车轮多边形动态量化识别的研究较少.现有的多边形车轮检测方法可分为静态检测与动态检测两类,传统的静态检测方法中接触式测量方法包括轮径尺测量法,不落轮镟床测量,车轮粗糙度测量仪等[5-6].静态测量方式虽然具有较高的测量精度但普遍存在占用车辆周转时间,劳动强度大,效率低等问题[7],然而,动态检测能有效弥补以上不足,是未来列车车轮缺陷检测的发展趋势.动态检测分为地面式和车载式,地面式检测系统为当列车慢速经过时对车轮外形及故障进行检测.Gao 等[8]结合激光位移传感器和涡流传感器搭建测量装置对列车通过时的车轮直径进行动态测量,通过现场试验验证,该测量系统能够满足车轮直径动态测量的精度要求.Gong 等[9]提出了一种基于结构光视觉的车轮直径测量方法,该方法中包含结构光视觉的三维重建和图像处理等关键技术,并分别在实验室和现场验证了测量方法的准确性和鲁棒性.地面式检测方法不能实现连续在线监测,无法及时掌握多边形车轮磨耗的发展趋势.车载式车轮动态检测方法可实现车轮状态实时监测,且设备结构简单,其中车载监测的轴箱加速度是主要的数据来源[10-11].丁建明等[12]基于轴箱垂向振动加速度提出一种车轮不圆顺车载动态检测方法,并通过动力学仿真数据对该方法的可靠性和工程适应性进行了验证.Song 等[13]研究了轴箱加速度与车轮多边形在时域、频域和高速条件下的定量关系,结果表明轴箱加速度及其频率与多边形车轮阶次和幅值有定量关系,可实现车轮多边形及损伤程度检测.然而,上述基于轴箱加速度的车载式检测方法在检测多边形车轮幅值的精度方面还有待进一步研究.

近年来,随着列车监测大数据的不断累积,基于数据驱动算法的损伤识别取得了显著成效,在车轮损伤识别方面,王其昂等[14]设计卷积神经网络结构识别列车车轮是否出现多边形损伤,在高铁车轮损伤识别中表现出较高的识别精度且具有轻型高效的特点.Chi 等[15]提出了一种基于数据驱动的方法来预测多边形磨损程度,研究成果可用于指导实际车轮维护优先级分配.此外,基于神经网络的损伤识别方法在其他领域也取得了显著成果,极限学习机(extreme learning machine,ELM)及其改进算法作为一种快速且有效的学习方法已广泛应用于各领域研究中[16-18],Hu 等[19]提出了一种ELM 的新型改进方法,可以快速、准确地识别旋转机械的故障状态.Cai 等[20]基于灰狼优化算法提出了一种参数学习策略优化核极限学习机 (kernel extreme learning machine,KELM),并在多个实际应用中验证了算法性能.但总体而言,数据驱动算法在列车车轮损伤识别方面报道较少.

本文提出一种基于列车轴箱垂向加速度的车轮多边形磨耗识别方法,首先从轴箱加速度中分析出多边形车轮阶次信息,实现主要阶次(即多边形车轮磨耗的较大幅值对应阶次)识别,然后建立基于遗传变异粒子群 (genetic mutation particle swarm optimization,GMPSO)优化多核极限学习机 (multiple kernel extreme learning machine,MKELM)的多边形车轮磨耗幅值识别模型,选用各主要阶次对应的加速度幅值与轴箱加速度信号熵特征作为模型的输入特征,输出多边形车轮阶次对应的磨耗幅值,从而实现车轮多边形磨耗定量识别,以期为车轮镟修及超限预警提供参考数据.

1 方法与理论分析

1.1 优化的MKELM

1.1.1 MKELM 方法

Huang 等[21]在单隐层神经网络的基础上提出ELM.由n维输入xi=[xi1,xi2,···,xin]T和l维输出yi=[yi1,yi2,···,yil]T组成N个样本,则含L个隐含层节点的神经网络可定义如下

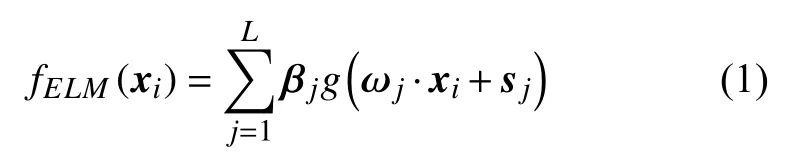
式中 βj=[βj1,βj2,···,βjl]表示隐含层节点的输出权值,ωj=[ωj1,ωj2,···,ωjn]为隐含层节点的输入权值,g(x)为激活函数,sj=[s1,s2,···,sL]T表示隐含层节点偏差.

输出矩阵又可简化表示如下

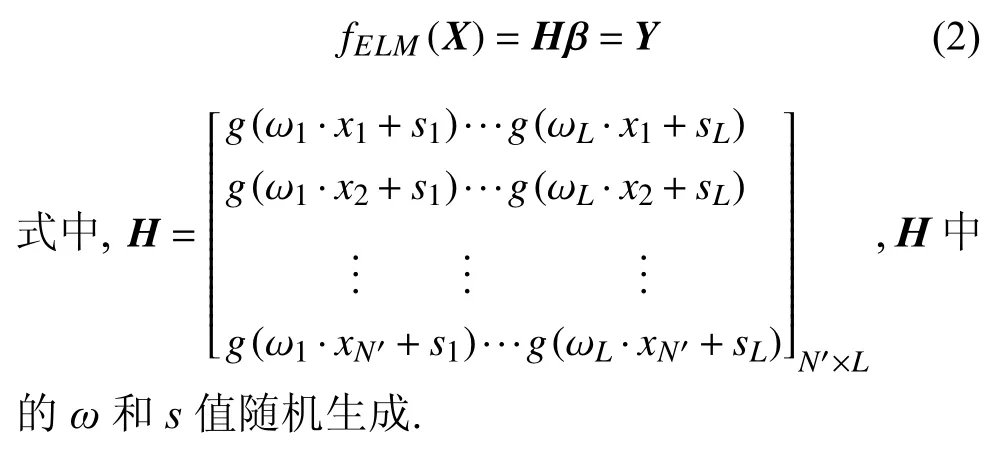
给定正则化系数S,式(2)中输出权值的最小二乘解为

极限学习机虽具有网络结构简单、训练速度快等优点,但仍存在需要预先设定隐含层节点个数,随机给定输入权值 ω 和隐含层偏差s等不足[22],与ELM 相比,KELM 方法在网络训练过程中,仅需选择适当的核参数与正则化系数,通过矩阵运算,获得网络的输出权值[23].对于一个测试样本x,ELM 输出函数的核矩阵公式定义如下

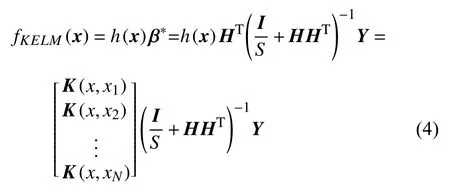
式中,K(xi,xj)为核函数.

但在实际应用中很难寻找最合适的核函数,基于常用的核函数特点,将KELM 机拓展为MKELM[24],本文采取多核函数线性加权组合的方式构建MKELM,选择分别如式(5)～式(7)所示的三阶多项式、高斯和小波三种核函数加权组合构建复合核函数,如式(8)所示

式中,C0表示多项式核函数参数,σ表示高斯核函数的核宽度,a表示小波核函数参数,Ω(X,xk)为所定义的组合核函数,Ci为核函数对应的权重且C1+C2+C3=1.

集成三种类型核函数用于多边形车轮磨耗幅值识别的MKELM 表达式如下

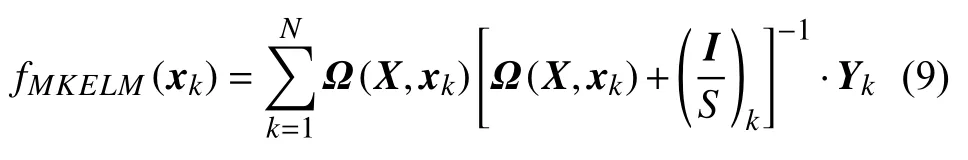
1.1.2 GMPSO-MKELM 方法

本研究中主要采用PSO 算法[25],并在优化过程中引入遗传算法的复制、交叉和变异策略来优化MKELM[26].PSO 算法的基本思想为:在可解空间中随机初始化一组优化问题解的“粒子”,每个粒子通过适应度函数计算适应度值来评估粒子质量,然后通过迭代的方式跟踪粒子的个体极值pi和全局极值pg改变自己的位置,直到搜寻到全局最优解.本文MKELM 的待优化参数包括核参数C0,σ和a,核权重C1和C2和正则项系数S.以上六个参数优化步骤如下.

(1)初始化GMPSO 算法参数,将验证集的均方根误差(root mean square error,RMSE)定义为寻优过程的适应度函数.

(2)利用PSO 算法对待寻优参数组成的种群U进行参数优化.粒子速度v和位置z更新公式如式(10)和式(11)所示,然后通过适应度函数对每个粒子进行评估

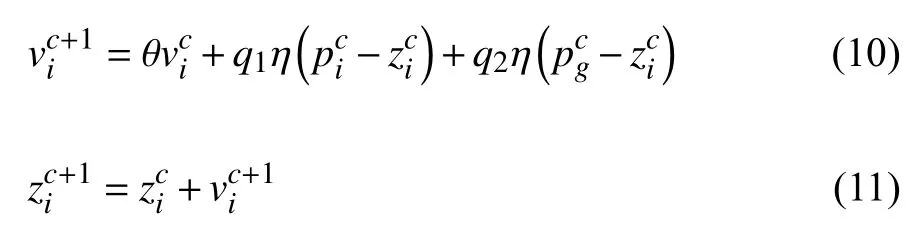
式中,θ 为惯性权重,q1和q2表示学习因子,η 取[0,1]之间的随机数,c表示迭代次数.

(3)根据适应度值对种群中粒子按升序排列并等分为“好”、“中”、“差”三类.然后引入遗传算法的复制、交叉和变异操作,将适应度值为“好”的粒子直接复制进入下一代,“中”、“差”适应度值的粒子分别进行交叉和变异操作.更新粒子个体极值pi和种群全局极值pg.

(4)转到步骤(2),循环迭代,直到达到最大迭代次数,得到最优粒子位置即可获得MKELM 的最优参数组合.

1.2 特征分析

本节介绍了所提出的多边形车轮检测方法中阶次分析以及磨耗幅值识别的特征提取方法,所选用的特征主要包含以下两方面:(1)多边形车轮各阶次对应的加速度幅值;(2)轴箱加速度信号熵特征.

1.2.1 阶次分析

本文方法针对列车匀速平稳条件下的多边形车轮进行阶次分析.首先,根据列车运行速度,计算车轮转动频率,然后由加速度传感器采样频率估计车轮旋转一周振动信号采样点数nsample,计算方法如下

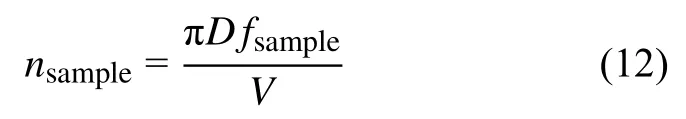
式中D为车轮直径,fsample为振动信号采样频率,V为列车运行速度.

按车轮旋转周期内信号采样点数为移动窗口长度划分轴箱垂向加速度信号时间序列,并对每个时间窗内的加速度信号进行阶次分析.首先,对轴箱加速度信号进行FFT 得到信号频率分布,然后,根据车轮转动频率计算得到加速度信号阶次与幅值,并先按幅值降序后阶次升序重新排列,最终筛选得到由多边形车轮引起的轴箱加速度信号主要阶次以及对应的加速度幅值.

1.2.2 熵理论

多边形车轮磨耗的阶次与幅值大小将直接影响轴箱垂向加速度信号的复杂度和不规则程度,不同阶次与幅值的多边形车轮引起的轴箱加速度时间序列复杂度越小,则熵值越小,反之,则熵值越大.本研究方法中引入模糊熵[27]和样本熵[28]量化振动时间序列复杂度,并将其作为多边形车轮幅值估计特征.

模糊熵和样本熵都是衡量信号复杂程度的特征指标,可用来描述多边形车轮引起的轴箱加速度信号特征.区别在于模糊熵中引入模糊隶属度函数,而样本熵中采用硬阈值判据.本研究分别从两方面衡量信号复杂程度,充分挖掘数据潜在特征.两种熵特征的计算步骤在文献[27-28]中详细介绍,计算流程如图1 所示.

图1 熵特征计算流程图Fig.1 Calculation flow chart of entropy characteristics

定义模糊熵FuzzyEn和样本熵SampEn计算公式分别如式(13)和式(14)所示

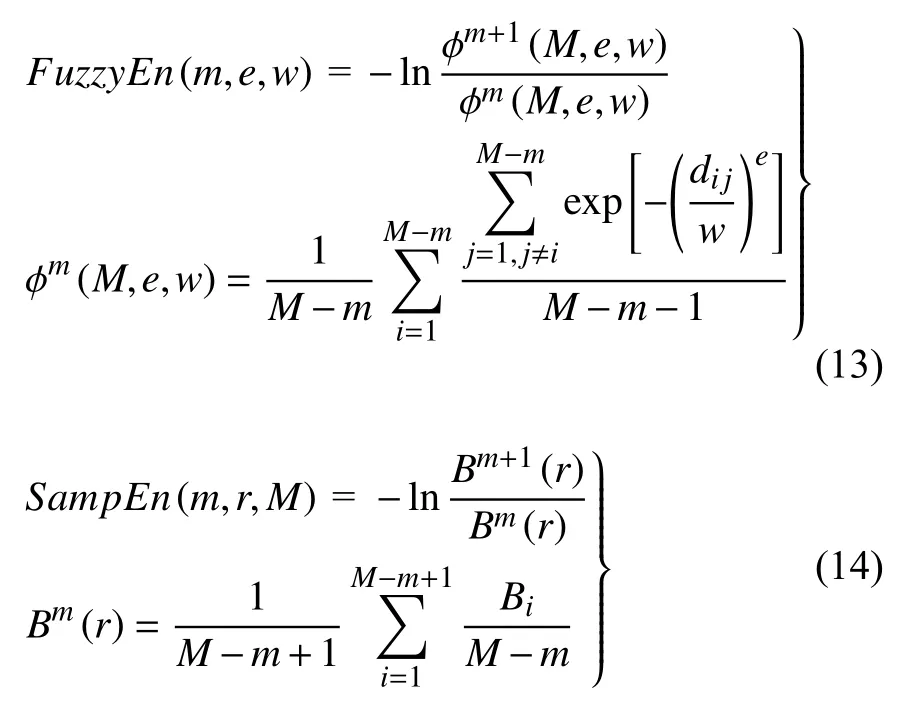
式中m表示模式维数,r表示相似容限阈值,M表示原始数据长度,Bi为向量之间距离小于r的数量,e和w分别表示模糊函数的边界梯度和相似容忍,dij表示向量间对应元素之差的最大绝对值.

1.3 多边形车轮识别方法

本文所提出的基于GMPSO 优化MKELM 模型定量识别多边形车轮磨耗的算法流程如图2 所示.该方法基于列车轴箱垂向加速度信号,识别多边形车轮磨耗的阶次与幅值,主要包含以下步骤.

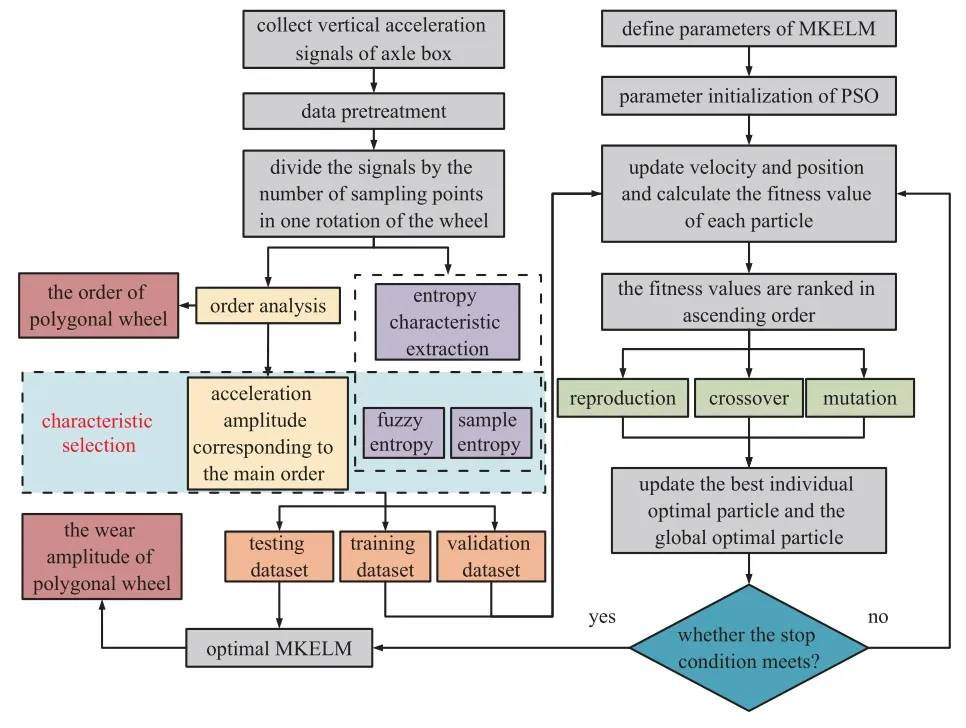
图2 多边形车轮识别算法流程图Fig.2 Flow chart of polygonal wheels identification algorithm

(1)振动信号采集:在轴箱合适位置布设加速度传感器采集由多边形车轮引起的加速度信号,并完成数据滤波与异常数据剔除等数据预处理.在数据滤波方面,根据列车运行速度V,多边形车轮不平顺波长范围 λ 所对应的激励频率f可通过下式计算得到

以此确定轴箱加速度滤波带宽,减少由轨道不平顺引起的干扰.

(2)阶次分析:根据列车速度计算车轮转频,以车轮旋转周期划分轴箱加速度信号,对单个周期信号进行FFT,获取多边形车轮阶次与相应的加速度幅值.

(3)特征提取:多边形车轮幅值识别的特征集构成分为两部分,其一,将步骤(2)中获取的阶次谱按先幅值降序后阶次升序重新排列筛选出主要阶次,以主要阶次对应的加速度幅值为部分特征;其二,计算每个车轮旋转周期内加速度信号的模糊熵和样本熵特征.

(4)优化MKELM 模型构建:以步骤(3)所提取特征为输入集,车轮磨耗幅值为输出集,构建模型样本集并划分训练集与测试集.然后,设定MKELM 参数寻优范围,将训练集与验证集输入MKELM 模型,采用GMPSO 算法寻优迭代至最大次数后停止,输出最优参数组合并重新训练网络.

(5)多边形车轮磨耗幅值识别:将测试集输入到参数优化后的MKELM 模型,识别出多边形车轮主要阶次对应的磨耗幅值.

2 车轮多边形磨耗识别仿真分析

2.1 机车动力学模型

结合国内某型电力机车实际车辆结构与动力学模型参数,在SIMPACK 软件中搭建机车动力学模型,如图3 所示.所建立的机车车辆系统模型由车体(1 个)、构架(2 个)、轮对(4 个)、牵引电机(4 个)和牵引拉杆(2 个)组成,其中,车体与两构架之间通过二系悬挂连接,构架与轮对之间通过一系悬挂连接,各部件间悬挂连接均采用弹簧阻尼系统模拟.轮对、构架和车体均考虑纵向、横向、垂向、摇头、点头和侧滚6 个自由度,牵引拉杆考虑5 个自由度(侧滚未考虑),电机考虑垂向和点头2 个自由度[29].车辆系统动力学仿真计算详细参数设置见文献[30-31].

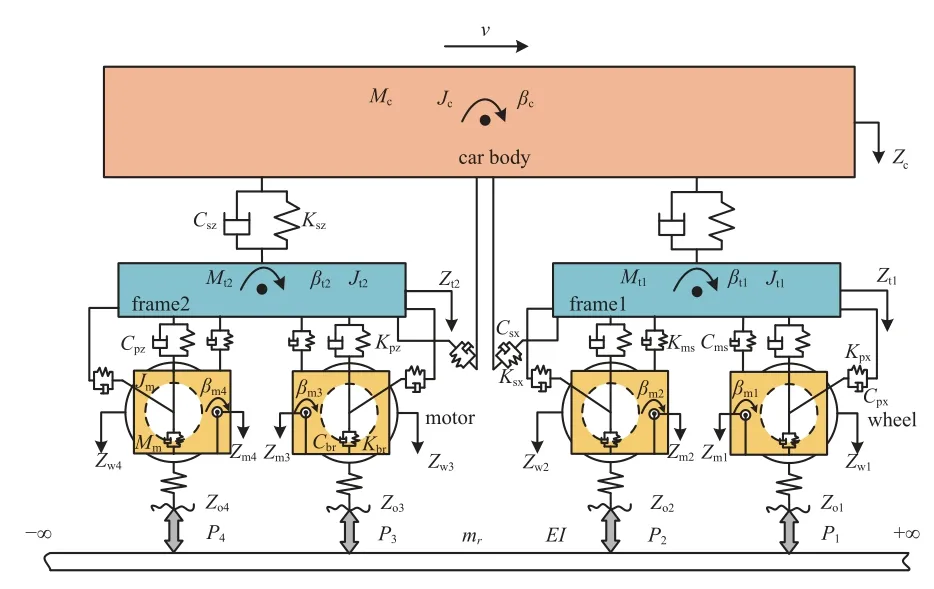
图3 机车动力学模型Fig.3 Locomotive dynamic model

2.2 多边形车轮构造

幅值和阶次是描述车轮多边形磨耗的主要参数,仿真研究中采用不同频率和幅值谐波叠加的方式构建多边形车轮,即

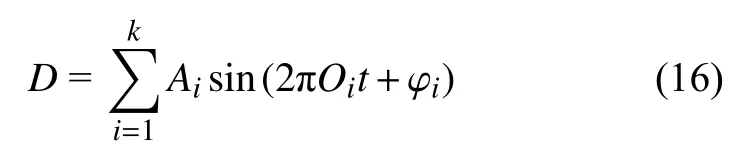
式中,t表示采样周期,φi表示谐波对应的初始相位角,谐波频率Oi的生成范围设定为10～20 的正整数,谐波幅值Ai设定为0.01～0.1 mm 范围内的随机数[1].

采用k=3 组随机匹配的谐波频率和幅值构建10 个多边形车轮,如图4 所示,将其输入到机车动力学模型中进行动力学仿真分析.

图4 仿真多边形车轮Fig.4 Simulated polygonal wheels

2.3 仿真多边形车轮识别

本节通过仿真分析验证多边形车轮识别模型的有效性,设定车辆以60 km/h 匀速运行于直线路段,同时采用美国五级谱模拟轨道不平顺.在图4 给定的多边形车轮磨耗激励作用下,计算得到了轴箱垂向加速度响应,部分加速度时域信号(2 kHz 采样频率)如图5 所示.

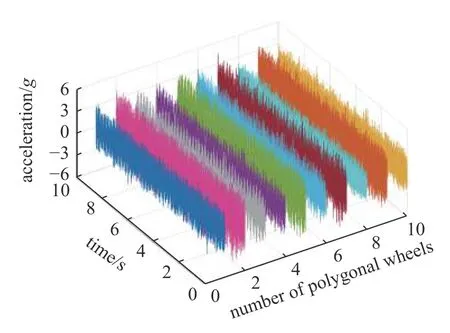
图5 轴箱垂向加速度时域信号Fig.5 Time-domain vertical acceleration signals of axle box

首先,进行轴箱加速度采样信号预处理,根据所提出的数据滤波带宽设置方法和仿真多边形车轮主要阶次范围,设置带通滤波上、下截止频率分别为42 Hz 和85 Hz.然后,开展多边形车轮阶次分析,依次对单个车轮旋转周期内的加速度信号进行FFT,准确识别出各多边形车轮3 个主要阶次,同时统计出各阶次对应的加速度幅值,由于线路不平顺和车辆结构振动传递的影响会导致同一阶次对应的加速度幅值在不同时间窗中存在细微差异.图6 展示了其中单个车轮旋转周期的十个多边形车轮阶次识别结果,通过与所构造的真实值对比,结果表明均实现了阶次的准确识别.然后,计算各时间窗内加速度信号的模糊熵和样本熵特征,由阶次对应的加速度幅值和熵特征组成的N×5 维输入特征集xi与多边形车轮磨耗幅值组成的N×3 维输出集yi构建样本集{xi,yi},i=1,2,···,N.在仿真研究中共采集N=6150个样本,随机划分5000 个为训练集,1000 个为验证集,150 个为测试集.

图6 多边形车轮阶次识别结果Fig.6 The order identification results of polygonal wheels

将训练集与验证集用于多核极限学习机参数寻优,迭代寻优过程如图7 所示.从图7 中可以看出,迭代次数达到123 次后验证集的RMSE 保持恒定,此时输出MKELM 模型的全局最优参数组合.在此基础上,重新训练网络模型并将测试集输入最优MKELM 中验证多边形车轮磨耗幅值识别精度,其中,仿真数据分析分别选用3 组测试集,每组50 个样本进行验证.图8 展示了其中一组测试集的识别结果,图中3 个连续幅值为一组表示同一多边形车轮主要阶次对应的磨耗幅值,从图8 中可以直观地看出,采用优化MKELM 模型识别的多边形车轮幅值与真实值具有较高的拟合度,3 组测试集的RMSE统计结果分别为0.001 8,0.003 7 和0.001 0,证明了本文所提出的识别方法不仅表现出较高的识别精度而且具有较好的稳定性.

图7 参数组合寻优迭代过程Fig.7 Iterative process of parameter combination optimization

图8 多边形车轮磨耗幅值识别结果Fig.8 The wear amplitude identification results of polygonal wheels

此外,考虑科学的训练集样本数以适应多边形车轮定量检测的需要,利用仿真分析的样本集进一步分析样本数量对多边形车轮磨耗幅值定量识别的影响.统计5 个测试集随着训练样本数量变化,多边形车轮磨耗幅值识别结果的RMSE 变化规律如图9 所示.从图中可以看出,随着有效训练样本数量增加,5 个测试集的识别精度均呈不断提高的变化趋势.因此,所提出的识别算法在应用过程中应尽可能地增加有效试验样本数量,以提高多边形车轮磨耗幅值的识别精度.

图9 不同训练集样本数量的识别误差Fig.9 Identification errors of the different number of training samples

为进一步验证本文所提出的优化MKELM 方法的泛化能力,表1 中分别对比了ELM 和KELM 模型识别多边形车轮磨耗幅值的RMSE 统计结果,其中,由于ELM 输入权值和隐含层偏差随机生成,会导致输出结果不稳定,故以10 次输出结果的RMSE平均值为ELM 识别精度统计结果;KELM 分别选用高斯、三阶多项式和小波三种常用核函数进行对比验证.从对比结果可以看出,本文所提出的优化MKELM 模型在三组测试集中均表现出更高的识别精度.此外,基于ELM 的识别模型在时间成本上具有突出优势,为了证明本文识别方法在实际应用中具有应用潜力,表1 中统计了不同对比模型的测试集检测时间.其中,本文所提出的优化MKELM 检测时间为0.017 3 s,可满足工程应用需求,与其他识别模型相比,虽然检测时间有所增加,但获得了更高的识别精度.综上所述,GMPSO-MKELM 模型在多边形车轮磨耗幅值识别方面具有较强的泛化性能和应用潜力.

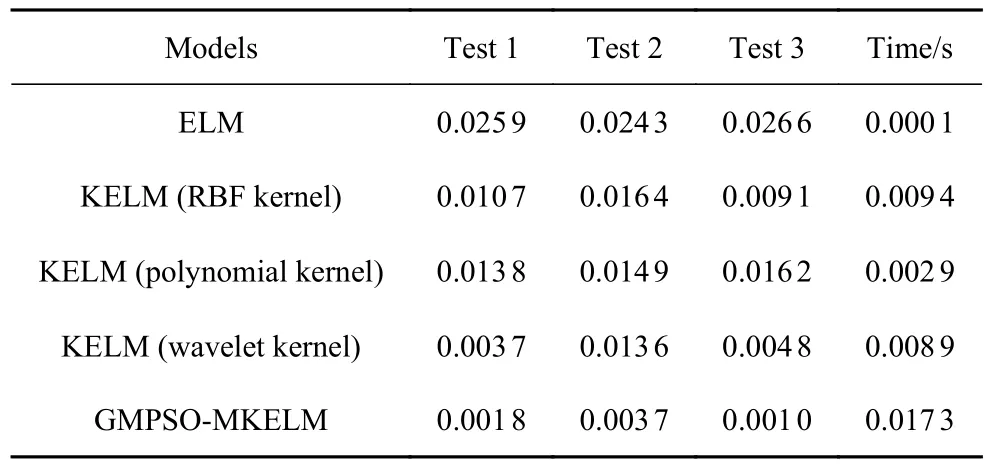
表1 不同模型的磨耗幅值识别RMSE 与时间Table 1 Identification RMSE and time of wear amplitude with different models

3 实例分析

为了充分证明本文所提出的车轮多边形磨耗识别方法的有效性和适用性,保证识别模型可应用于实际场景中,本节利用从国内某机务段运营的电力机车采集的实测数据进行试验验证.

3.1 现场试验

所选用的国内某型试验机车如图10(a)所示,该机车长期运营后,存在车轮多边形磨耗.试验中选用镟修前和镟修后机车四轴车轮为研究对象,在机车轴箱的合适位置布设加速度传感器测量轴箱垂向加速度响应,如图10(b)所示.为验证识别模型对轻度多边形车轮磨耗的检测能力,选用镟修后车轮为研究对象,车轮镟修方式采用如图10(c)所示的不落轮镟床镟修,其中四轴左侧车轮经镟修后仍存在多边形现象,而右侧车轮经镟修后车轮多边形基本消失,因此,在实例研究中,以镟修前四轴左右侧车轮和镟修后右侧车轮为识别对象.现场利用如图10(d)所示的Müller-BBM 车轮粗糙度测量仪对机车多边形车轮周向轮廓进行测试.

图10 现场试验.(a)试验机车;(b)轴箱加速度测量;(c)车轮镟修;(d)多边形车轮测量Fig.10 Field testing.(a)Testing locomotive;(b)measurement of axle box acceleration;(c)wheel lathing;(d)measurement of polygonal wheels

车轮镟修前后的采样数据经FFT 后得到阶次和磨耗幅值测试结果如图11 所示,其中,四轴左侧车轮多边形磨耗主要阶次为16～18 阶,对应的幅值分别为0.033 6 mm,0.082 9 mm 和0.068 0 mm,四轴右侧车轮多边形磨耗主要阶次为17～19 阶,对应的幅值分别为0.036 7 mm,0.033 2 mm 和0.016 7 mm.四轴左侧车轮镟修后仍存在主要阶次为15～17 阶,幅值分别为0.003 1 mm,0.009 0 mm 和0.001 8 mm 的多边形磨耗.以上三个车轮表现出不同程度的多边形磨耗,且各自主要阶次分布在不同区域,有益于充分验证多边形车轮识别模型的适用性.

图11 试验多边形车轮阶次与磨耗幅值测试结果Fig.11 The order and wear amplitude testing results of polygonal wheels

3.2 多边形车轮识别

以4096 Hz 采样频率采集列车分别以40 km/h,60 km/h,80 km/h 速度运行过程中的轴箱垂向加速度响应,在信号预处理中,去除由于焊缝及其他轨道病害引起的异常冲击信号区段,并按不同速度等级设置相应的滤波带宽完成数据滤波.部分加速度信号时域测试结果如图12 所示,可以看出车轮镟修前左右侧多边形车轮引起的轴箱垂向加速度响应无明显差异,而镟修后加速度响应显著减小.试验中共采集N=850 个数据样本,其中随机划分600 个为训练集,100 个为验证集,150 个为测试集.在此基础上,开展多边形车轮参数的定量识别研究.根据本文中阶次分析方法,统计各样本所包含的多边形车轮阶次和对应的加速度幅值信息,图13 展示了单个样本的识别结果,从图中可以看出,根据加速度幅值大小可确定多边形车轮所包含的主要阶次.

图12 实测轴箱垂向加速度信号Fig.12 Field test vertical acceleration signals of axle box

图13 多边形车轮阶次识别结果Fig.13 The order identification results of polygonal wheels

接下来,利用各样本计算出的多边形车轮主要阶次对应的加速度幅值与各样本熵特征构建多边形车轮磨耗幅值识别特征集,然后将训练集与验证集输入优化MKELM 模型中寻优参数组合并训练网络,最后,将测试集输入最优MKELM 中进行验证.实测数据分析同样选用3 组测试集,每组50 个样本进行验证.图14 为其中一组测试集识别结果对比,从图中可以看出本文所提出的多边形车轮幅值识别方法具有较高的识别准确率,3 组测试集的RMSE统计结果分别为0.018 3,0.013 4 和0.016 5,以此证明了本文所提出的多边形车轮磨耗识别方法在实际应用中的适用性,同时也再次证明了该方法的识别精度和算法稳定性.

图14 多边形车轮磨耗幅值识别结果Fig.14 The wear amplitude identification results of polygonal wheels

表2 中采用实测数据集同样对比了所提出的优化MKELM 模型与ELM 和KELM 模型识别多边形车轮磨耗幅值的识别精度和时间,从统计结果可以看出本文所提出的优化MKELM 模型在三组测试集中用较少的时间成本换取了更高的识别精度,再次证明了GMPSO-MKELM 模型的泛化性能.因此,本文所提出的GMPSO-MKELM 在实际中更具有应用潜力.

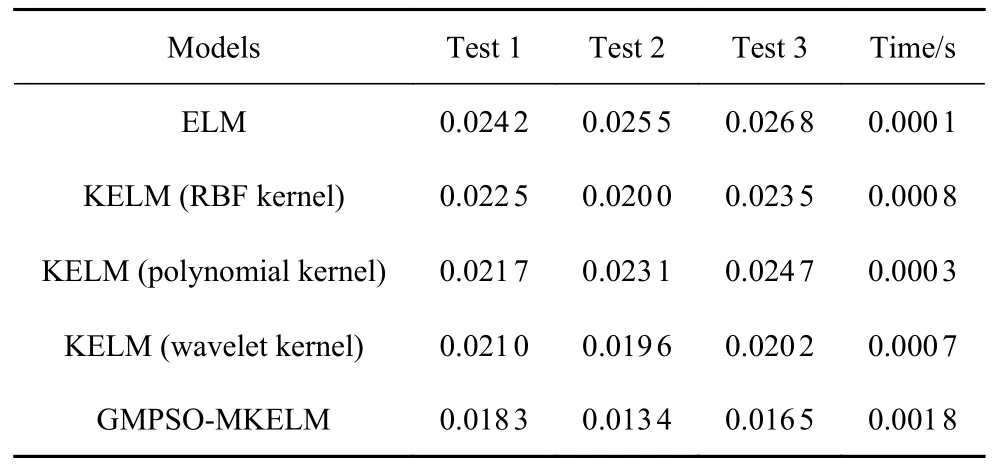
表2 不同模型的磨耗幅值识别RMSE 与时间Table 2 Identification RMSE and time of wear amplitude with different models

4 结论

本文提出了一种多边形车轮定量检测方法,基于列车轴箱垂向加速度能有效识别出车轮多边形磨耗阶次和幅值,主要研究结论如下:

(1)本文所提出的识别模型适用于列车匀速平稳运行状态下准确识别车轮多边形磨耗主要阶次与幅值;

(2)通过构建的有效特征组合实现了车轮多边形磨耗幅值的精准识别,可实现RMSE 为0.001 0(仿真结果)与0.013 4 (试验结果)的识别精度,且均具有较好的算法稳定性;

(3)搭建了车轮多边形磨耗幅值识别的GMPSOMKELM 优化模型,优化后的模型相比于ELM 和KELM 具有更高的识别精度,且在时间成本上表现出良好的工程应用前景.

本研究基于神经网络模型拓展了多边形车轮定量识别的研究思路,未来可利用车载监测大数据训练模型,并将识别模型进一步推广应用于列车车轮状态实时在线监测.