基于DRBF-EKF 算法的车辆质心侧偏角与路面附着系数动态联合估计1)

李韶华 王桂洋 ,2) 杨泽坤 , 王雪玮

* (石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

† (石家庄铁道大学河北省交通工程结构力学行为演变与控制重点实验室,石家庄 050043)

** (石家庄铁道大学机械工程学院,石家庄 050043)

引言

建立准确的车辆模型及高精度关键状态参数估计是实现车辆精确控制的前提和基础[1-3].四轮独立驱动 (four-wheel independent drive,4WID)电动汽车具有独立驱动的轮毂电机和内置传感器,相对于传统车辆可以实现更丰富多样的状态估计算法和控制策略[4-6].

在车辆状态参数估计方面,车辆侧偏角是提高稳定性的技术基础[7-11].扩展卡尔曼滤波和无迹卡尔曼滤波是最常用的车辆状态估计方法.文献[11]在常规工况下利用卡尔曼滤波方法对侧向车速进行估计,该估计器虽然能够准确地估计侧向车速,但车辆工作在非线性区域时会出现较大估计误差.Cheng等[12]提出了一种基于积分校正融合的自适应平方根立方卡尔曼滤波器(ASCKF)估计器,通过考虑传感器未知有色噪声,补偿车辆非线性动力学引起的估计误差,提高车辆侧偏角估计精度.赵万忠等[13]采用无迹卡尔曼滤波算法对汽车质心侧偏角、横摆角速度、路面附着系数等状态参数进行估计,提高了估计精度.利用车载传感器信息进行车辆状态参数估计也是当前的研究热点.Xia 等[14]基于车辆运动学模型进行侧滑角估计,简化惯性导航系统的速度和姿态误差,提高了估计精度.张征等[15]利用低成本普通车载传感器信息,电机输入信息和驾驶信号,采用无迹卡尔曼滤波算法对质心侧偏角进行估计,利用硬件在环实时仿真平台进行了验证.利用动力学方法进行车辆质心侧偏角估计时,需要充分地考虑轮胎与路面的相互作用关系,估计精度依赖于建立精确的车辆模型.

在轮胎-路面接触特性方面,常用的方法是设计观测器和卡尔曼滤波[16-18],熊璐等[19]利用车辆纵侧向激励,分别设计不同激励条件下的路面附着系数估计方法,通过车辆状态参数判断满足的激励条件,设计融合观测器进行估计结果融合.Cheng 等[20]提出了一种可以同时观察轮胎-路面摩擦系数和轮胎力的监控系统,通过模式切换观测器,估计车辆处于正常行驶、制动和转向等不同工况时的轮胎-路面摩擦系数.樊东升等[21]利用双容积卡尔曼滤波进行路面附着系数估计,进行了对接路面双移线工况仿真实验,验证了算法的有效性.随着人工智能技术在多个领域的不断发展,也越来越多地应用到了车辆研究领域中[22-30].王岩等[31]提出了一种基于支持向量机的智能轮胎路面辨识算法.伍文广[32]利用Carsim/Simulink 联合仿真,建立Elman 神经网络路面附着系数识别模型,与传统的BP 网络相比,降低了误差.林棻等[33]提出一种基于改进Keras 模型的路面附着系数估计方法,通过仿真验证表明所设计的估计器在路面附着系数估计中的有效性与可靠性.在利用深度学习和图像处理等方法来进行路面附着系数估计时,增加的视觉传感器会提高成本,也会增加算法的计算难度和处理时间.

本工作采用DRBF-EKF 神经网络方法,针对分布式驱动电动汽车,利用现有车载传感器,开发一种能够同时估计车辆质心侧偏角和路面附着系数的联合估计器,以期能够在保持精度的前提下,降低车辆质心侧偏角和路面附着系数估计过程中的计算复杂度和程序运行时间.

1 4WID 车辆动力学模型

4WID 车辆的四个轮毂电机内配有轮速和转角传感器,建立七自由度车辆动力学模型如图1 所示.

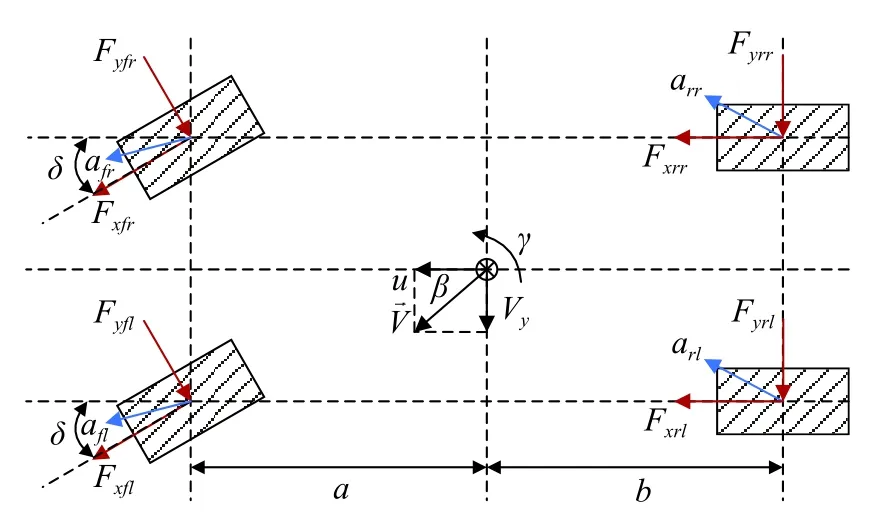
图1 四轮独立驱动车辆动力学模型Fig.1 Dynamic model for four-wheel independent drive vehicle

车辆的运动微分方程如下:

(1)纵向运动

(2)侧向运动

(3)横摆运动

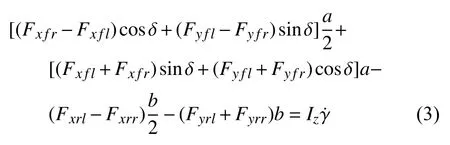
式中,δ 为前轮转角;ax为纵向加速度;vx,vy分别为纵向、侧向速度;m为整车质量;fl,fr,rl,rr分别为车辆的左前轮、右前轮、左后轮、右后轮;Fx,Fy分别为轮胎的纵向力、侧向力;a,b分别是质心至前后轴的距离;γ 为横摆角速度;Iz为整车绕z轴方向的转动惯量。

轮胎的纵向力和侧向力采用非线性的Dugoff模型计算,即

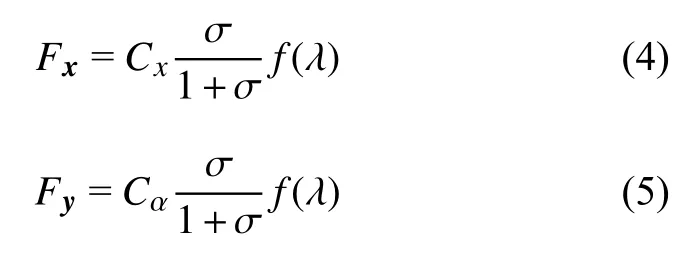
式中,σ 为车轮滑移率;Cx,Cα分别为轮胎纵向刚度、侧向刚度;λ 与摩擦系数 μ有关,μ 为轮胎与路面摩擦系数,α 为车轮侧偏角,函数f(λ)定义为

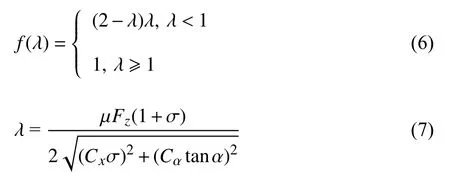
各轮胎垂直载荷

各车轮侧偏角

各车轮轮心纵向速度

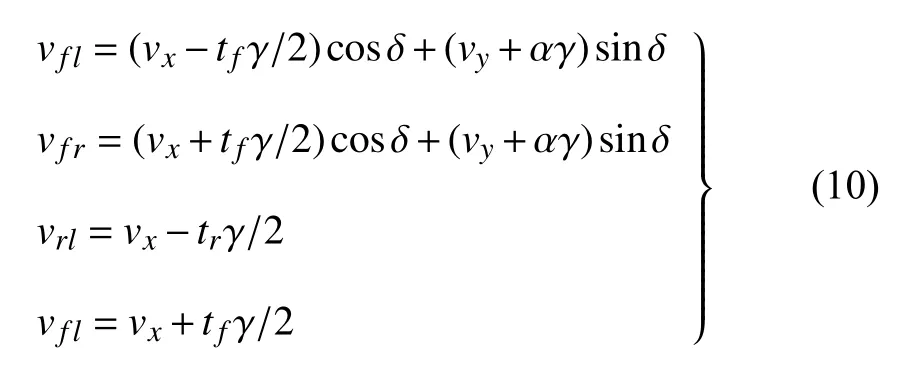
驱动工况,纵向滑移率

式中,tf,tr分别为前、后轮轴距;l为前后轴距离;Fzij为轮胎垂向力;h为质心高度;αij为轮胎侧偏角;vij为轮心纵向速度;wij为车轮角速度;R为车轮半径.

2 质心侧偏角和路面附着系数动态联合估计

由车辆的纵向和侧向车速,可得车辆质心侧偏角计算公式

根据车辆运动微分方程(1)～(3)和轮胎模型计算(4)～(11)确定车辆质心侧偏角估计器的输入为:[μ,δ,ax,ay],输出为车辆质心侧偏角 β.

在路面附着系数估计时,需要找到和路面附着系数最密切相关的参数作为输入量,由式(1)～式(11),可以确定路面附着系数μ和车辆行驶状态参数之间的函数关系[33]

路面附着系数估计和16 个参数都存在非线性关系,神经网络在处理非线性问题中输入量与输出量具有较强的相关性,因此利用PCA (principal component analysis)[34]多元统计方法进行主成分分析,提取最相关的特征参数,并进行数据降维,从而有效解决了RBF 网络在高维时难以寻找网络中心的问题,提高预测精度和预测效率,步骤如下:

(1)设有m条n维数据,数据预处理中心化X-;

(3)对协方差矩阵做特征值分解;

(4)选出最大的k个特征值对应的特征向量;

(5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P;

(6)Y=PX即为降到k维后的数据集.

取车速75 km/h,路面附着系数0.8,蛇形工况下,得到16 个车辆响应参数的400 组数据,对每两组数据之间利用SPSS 软件进行相关性分析.看两者是否相关主要看两个方面:显著水平以及相关系数.结果如图2 所示,蓝色表示各参数与路面附着系数 μ 的相关系数,值越大相关性越高.可以看出,路面附着系数与各车轮滑移率是完全相关的,与各车轮角速度也具有较强相关性,结合主成分分析,最终确定DRBF-EKF 神经网络在路面附着系数估计时输入和输出关系表达式为

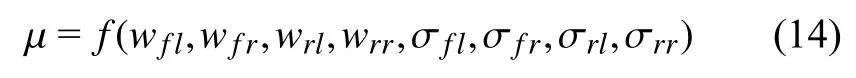
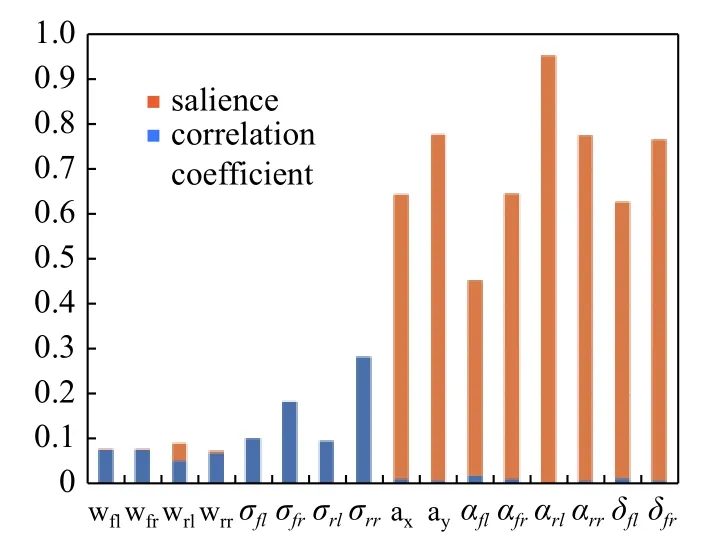
图2 PCA 相关性分析Fig.2 PCA correlation analysis

2.1 扩展卡尔曼滤波状态空间描述

扩展卡尔曼滤波的工作原理是以线性最小方差估计为依据,利用递推算法,通过被提取信号的测量值估算出所需信号.将Dugoff 轮胎模型代入车辆动力学方程,整理得到以下状态方程和测量方程

式中,状态变量x=[γ βvx]T,ay为观测量,系统输入量u=[Fxf Fxrδax]T.

真实值与预测值之间的误差协方差矩阵

卡尔曼增益Kk

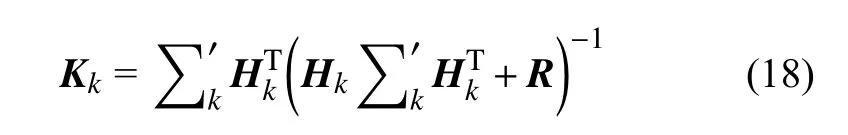
求解式(16)与式(17)的雅可比矩阵并对其进行系统离散化后得到状态转移矩阵

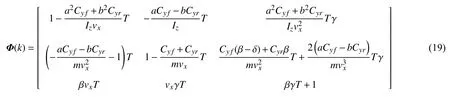
观测方程的雅可比矩阵如下

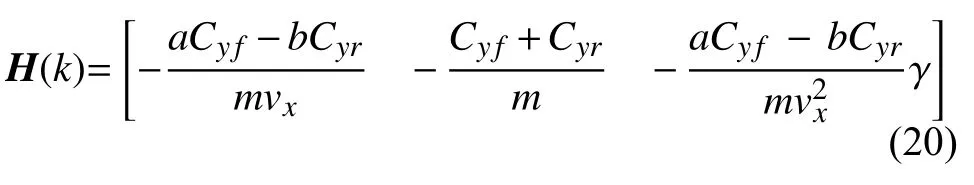
将 Φ(k),H(k)代入算法的表达式并进行迭代计算得到状态估计值.

2.2 基于K-means 算法改进的RBF 神经网络

在选择正确训练数据集的情况下,神经网络对于质心侧偏角的估计要优于运动和动力学方法[35].RBF 神经网络也是前馈神经网络,由输入层、隐含层和输出层三层神经元构成,能够根据样本自适应增加隐含层单元的个数,具有拟合精度高、速度快、泛化能力强等优点.首先利用K-means 算法确定初始RBF 神经网络的聚类中心及其个数[36],可以降低迭代次数,提高算法的运行速度.如果该样本到网络所有中心的距离都大于r,那么生成一个新的隐单元.如果不是,则将该样本归到距离r最小距离所属的类中,并且保持r不变;之后确定径向基函数的宽度以及隐含层到输出层之间的权值,最后输出结果.步骤如下:

(1)随机选择K个聚类中心;

(2)根据每个初始聚类中心的欧几里德平均距离,对剩余的数据集进行欧式距离计算,生成距离矩阵;

(3)在计算过程中,准则函数不断变化,直至函数收敛,得到K个原始聚类中心;

(4)样本Xt时网络的输出Yt为

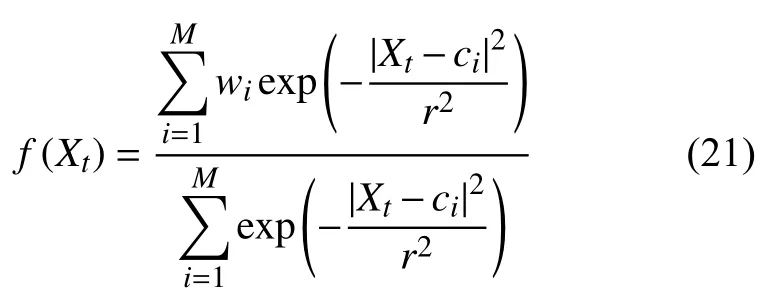
其中,宽度r的大小决定了RBF 网络的复杂度.r越小,聚类数目越多,计算量越大,精度也就越高;r越大,聚类数目少,计算量就相对较小,精度也会降低.

RBF 神经网络采用梯度下降的训练方法,目标函数为样本的输出误差,通过最小化误差实现对中心、宽度和网络权值的学习

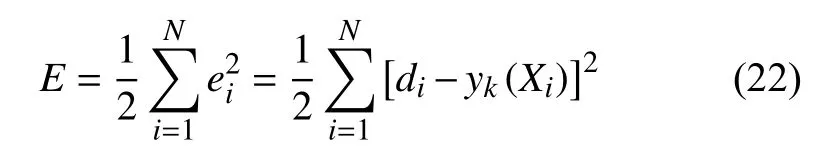
采用梯度下降训练方法,提高训练效率,各参数修正量与负梯度成正比

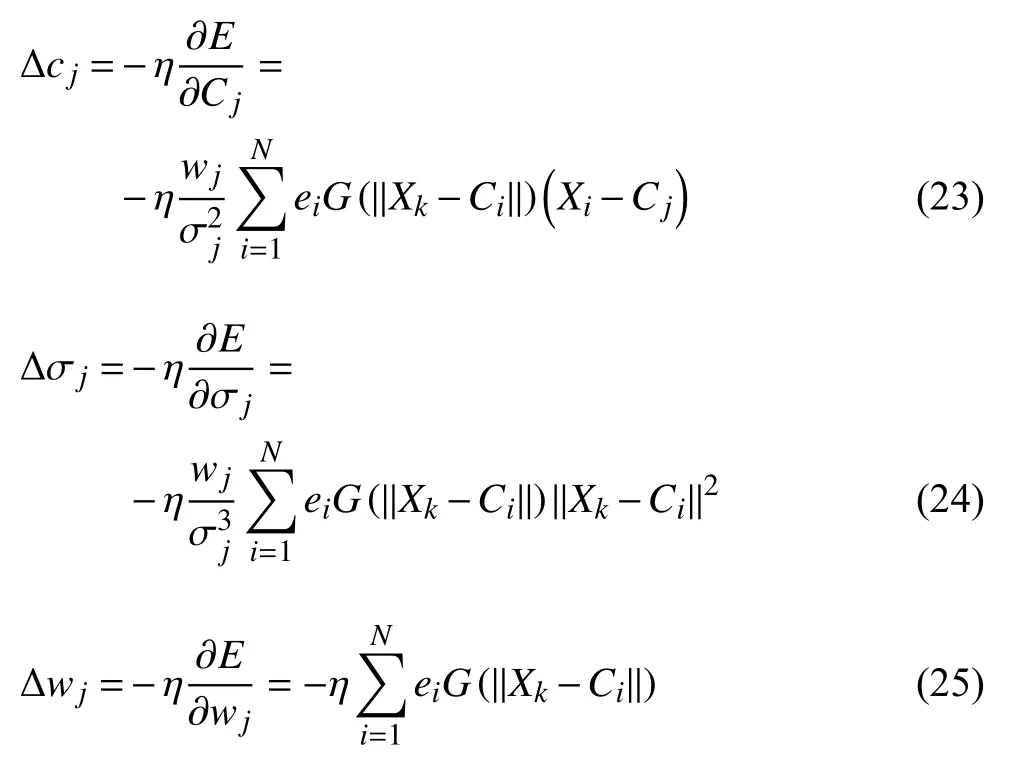
采用均方根误差(RMSE)作为神经网络预测性能评价函数,采用平均绝对误差(MAE)衡量车辆质心侧偏角和路面附着系数估计误差

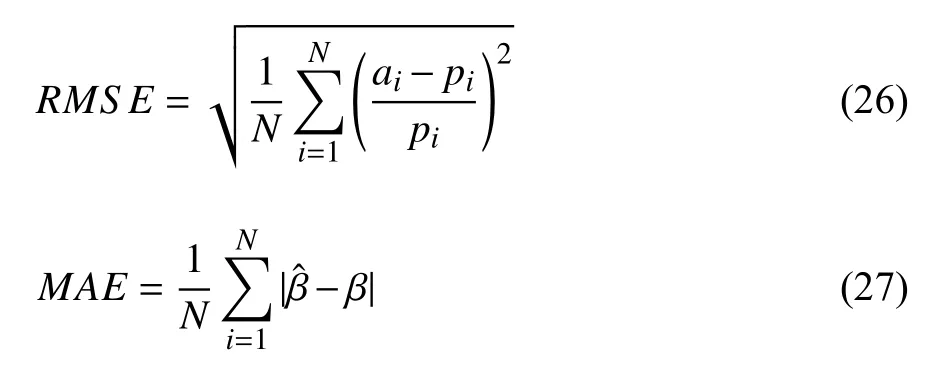
建立质心侧偏角和路面附着系数联合估计器,其中路面附着系数估计器的输出 μ 作为车辆质心侧偏角估计器的输入,车辆质心侧偏角估计器的输出纵向速度vx作为路面附着系数估计器的输入,结构框图如图3 所示.

图3 质心侧偏角与路面附着系数动态联合估计结构框图Fig.3 Structural diagram of dynamic joint estimation of sideslip angle and road adhesion coefficient

该估计器在路面附着系数估计时,为了解决RBF 网络在高维时难以寻找网络中心的问题,采用PCA 多元统计方法,提取主元特征参数,降低维度.由于实际路况复杂,采集车载传感器信息后往往含有较强的噪声信号,DRBF-EKF 算法首先利用 EKF进行滤波降噪后更有利于DRBF 建模精度的提高.通过实时反馈路面附着系数和车速,实现了变路面变车速工况下的车辆质心侧偏角和路面附着系数的联合估计.

3 仿真和实车实验

3.1 仿真

为了验证所提出的质心侧偏角与路面附着系数动态联合估计DRBF-EKF 算法,针对课题组的4WID 纯电动全线控沙滩车(UTV),利用CarSim 软件建立整车动力学模型,进行不同工况下的仿真.车辆主要参数见表1,工况及路面附着系数、车速设置见表2,仿真时间设为20 s.仿真发现,车辆在附着系数0.2 的路面上以90 km/h 速度行驶时会出现失稳现象,因此只保留了30,60 km/h 的数据.每种工况下,在可测参数向量和待估参数向量元素曲线上均匀取200 个点,对设置的8 种工况,得到可测参数向量和待估参数向量共1600 组数据用于神经网络模型的训练.

表1 车辆主要参数Table 1 Main parameters of the vehicle

表2 采集不同工况数据Table 2 Collect different working conditions data

(1)单一路面

式(15)中,路面附着系数和滑移率有很强的相关性,所以在求路面附着系数时,滑移率作为神经网络的输入.由式(12)可以看出,滑移率和轮毂电机转速有很强的相关性,而实验车辆也是轮毂电机驱动的,可以在不增加外在传感器的情况下测得车轮的转角和转速,所以,仿真试验中把轮毂电机的转速作为了质心侧偏角与路面附着系数动态联合估计器的输入.

工况一:车速60 km/h、蛇形工况、冰路面(μ=0.2)

在此种工况下,由Carsim 车辆动力学仿真软件得到的四个车轮角速度、前轮转角、车辆侧向加速度和纵向速度,如图示4(a)和图4(b)所示.采用所提出的DRBF-EKF 联合估计算法,得到的车辆质心侧偏角估计结果和误差如图4(c)和图4(d)所示,路面附着系数估计结果和误差如图4(e)和图4(f)所示.

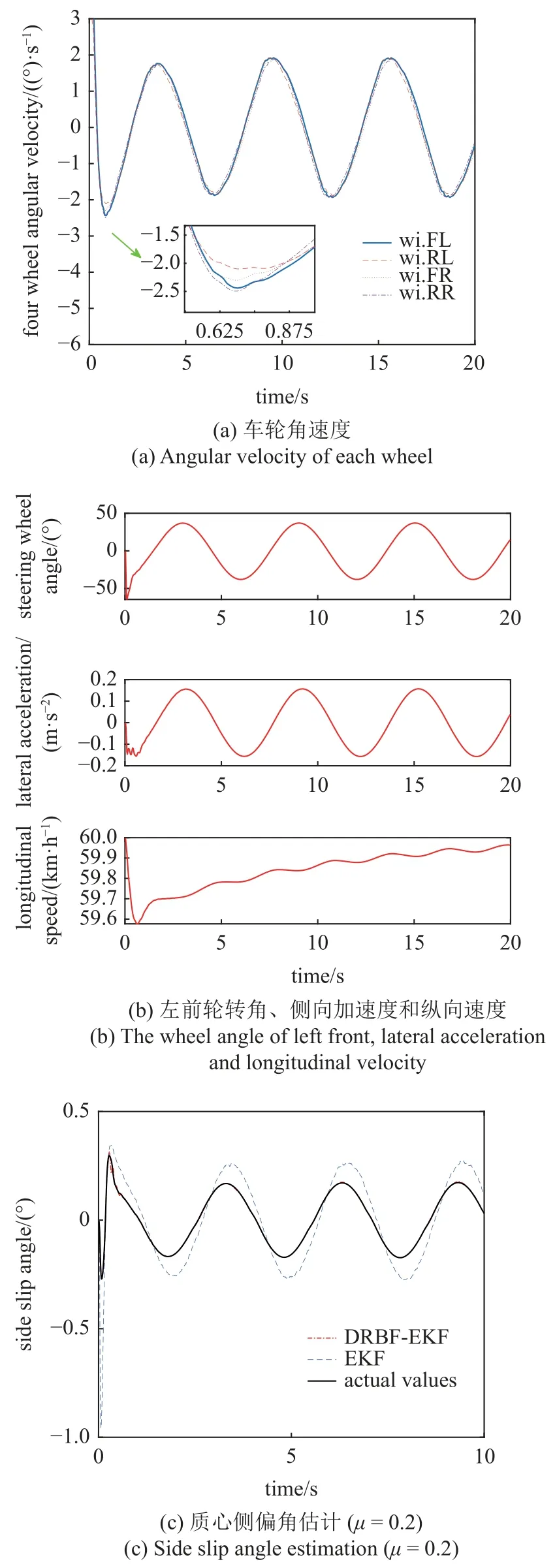
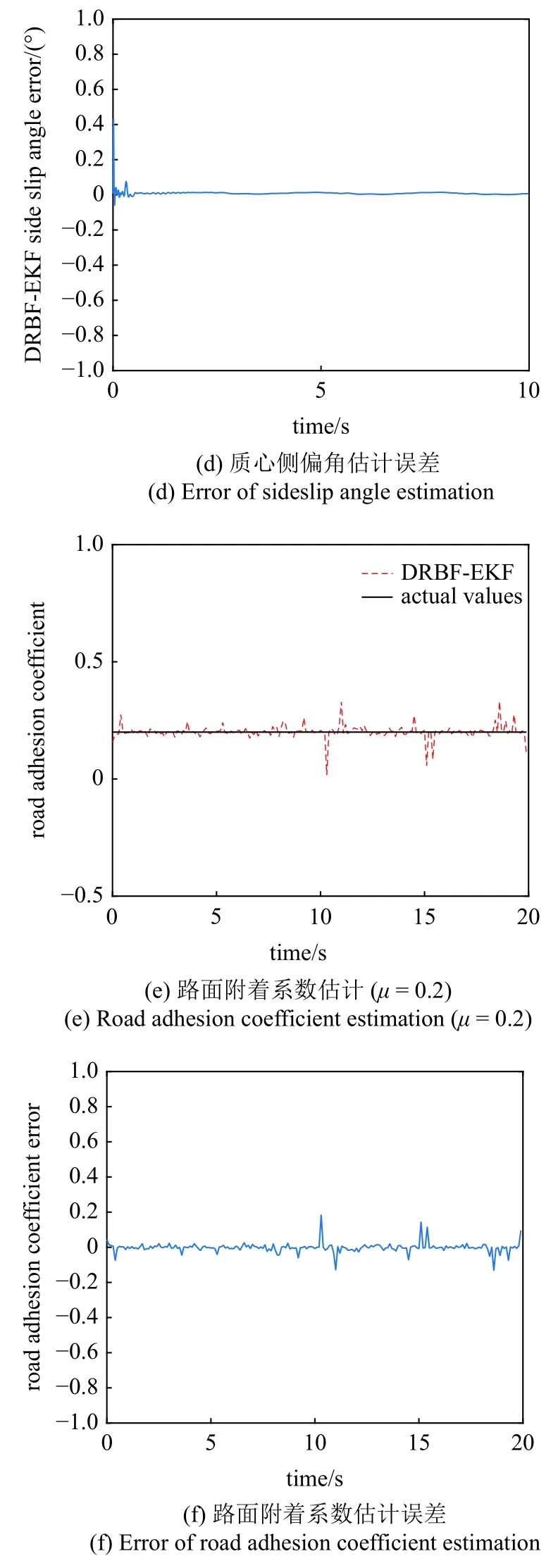
图4 冰路面质心侧偏角和路面附着系数联合估计Fig.4 Joint estimation of side slip angle and road adhesion coefficient on ice road

由图4 可以看出,所提出的DRBF-EKF 动态联合估计算法,在质心侧偏角估计时,与没有考虑路面附着系数和车速动态反馈的EKF 估计方法相比,在1 秒内就能较快地调整跟踪实际值.而EKF 方法需要不断调整模型估计值和传感器测量值的采信程度得到预测值,导致在开始阶段需要一定的调整时间.在后期联合估计方法仍能保持较高的估计进度,并且误差较小,由表3 可以看出质心侧偏角的平均绝对误差为0.029 3°.在路面附着系数估计时,DRBFEKF 动态联合估计结果平稳,误差在 ±0.1 以内.

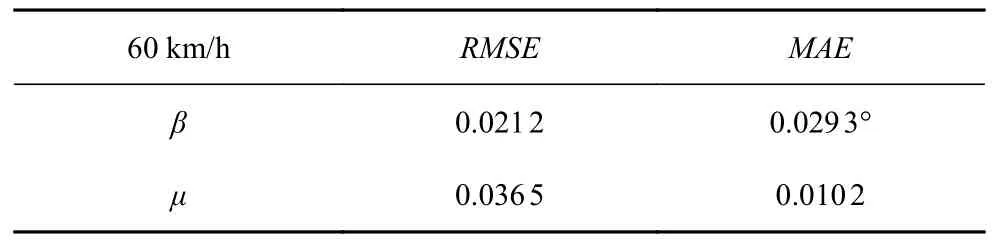
表3 车速60 km/h 冰路面估计误差Table 3 Error of vehicle speed 60 km/h on ice road

工况二:车速90 km/h、蛇形工况、干燥柏油路面(μ=0.85)

在此种工况下,车辆响应如图5(a)和图5(b)所示,DRBF-EKF 动态联合估计的结果如图5(c)和图5(d)所示,误差见表4.

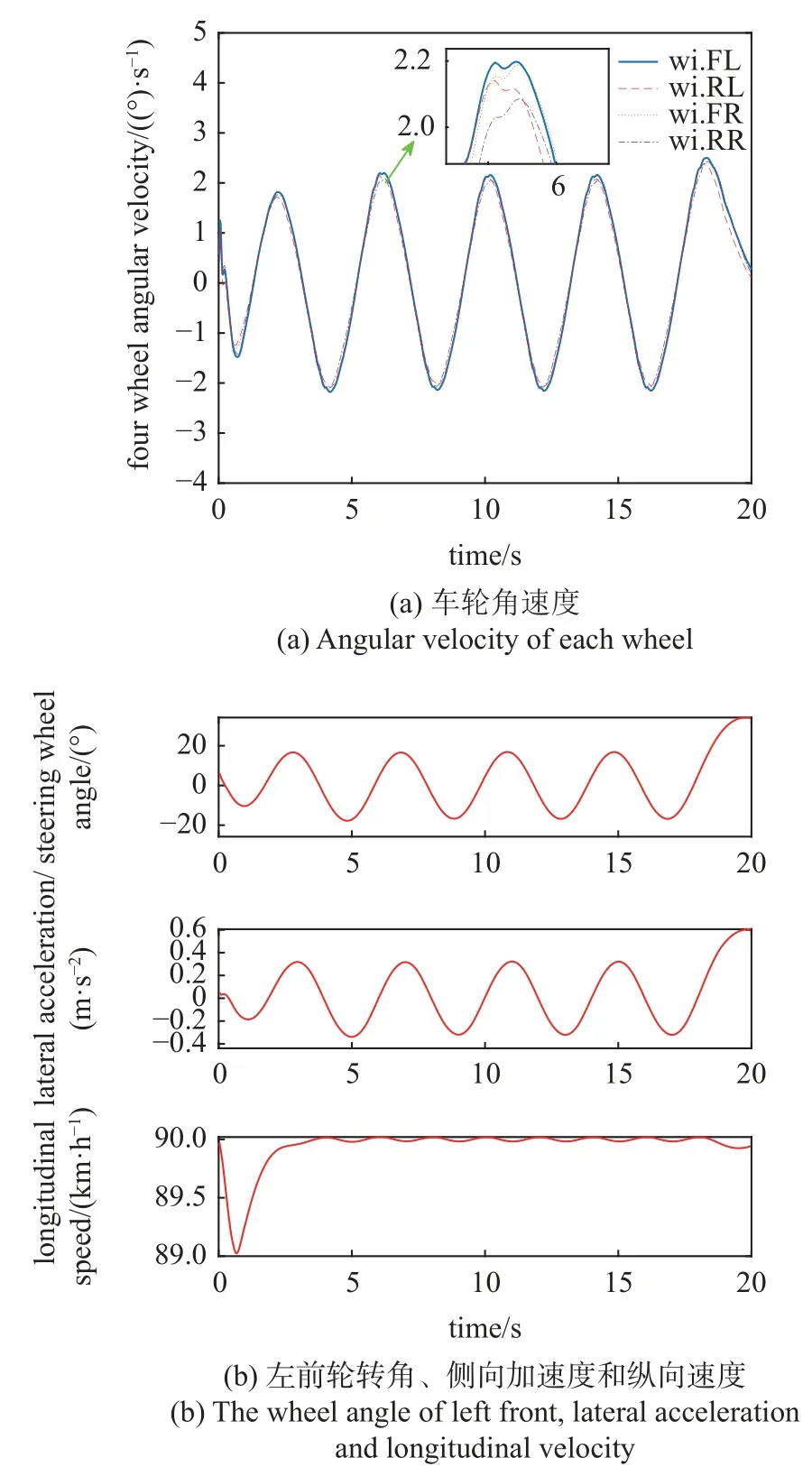
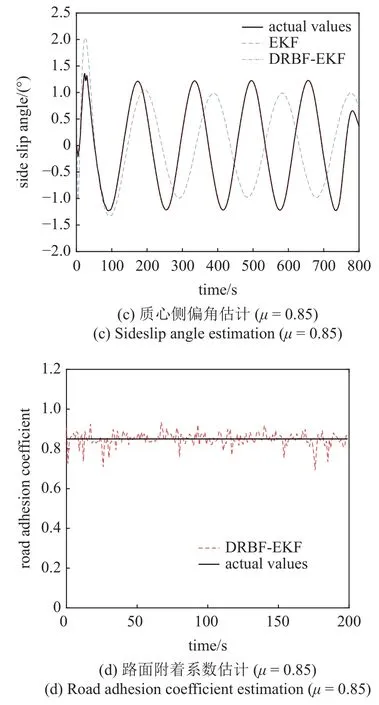
图5 干燥柏油路质心侧偏角和路面附着系数联合估计Fig.5 Joint estimation of side slip angle and road adhesion coefficient on dry asphalt road

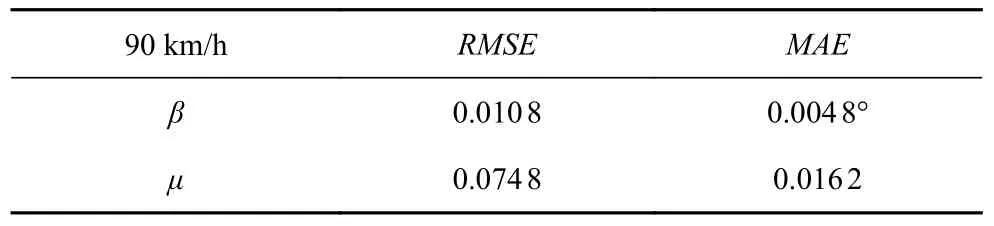
表4 车速90 km/h 干燥柏油路估计误差Table 4 Error of vehicle speed 90 km/h on dry asphalt

由图5 可以看出,在90 km/h 干燥柏油路面,在质心侧偏角估计方面,DRBF-EKF 动态联合估计方法与EKF 算法相比,具有较高的估计精度,质心侧偏角的平均绝对误差为0.004 8°.在路面附着系数估计时,车辆高速情况下比低速情况下估计精度有所降低,但估计结果总体平稳,估计误差稳定在误差在 ±0.15 以内.

(2)对接路面

工况一:车速60 km/h,由冰路面行驶到第10 秒时进入干燥柏油路面行驶10 秒,和由干燥柏油路面行驶到第10 秒时进入冰路面行驶10 秒时间.基于所提出的算法进行质心侧偏角和路面附着系数估计,结果如图6、图7 及表5 所示.

表5 车速60 km/h 对接路面估计误差Table 5 Error of vehicle speed 60 km/h on joint road

图6 由冰路面至干燥柏油路质心侧偏角和路面附着系数联合估计Fig.6 Joint estimation of sideslip angle and road adhesion coefficient from ice road to dry asphalt road

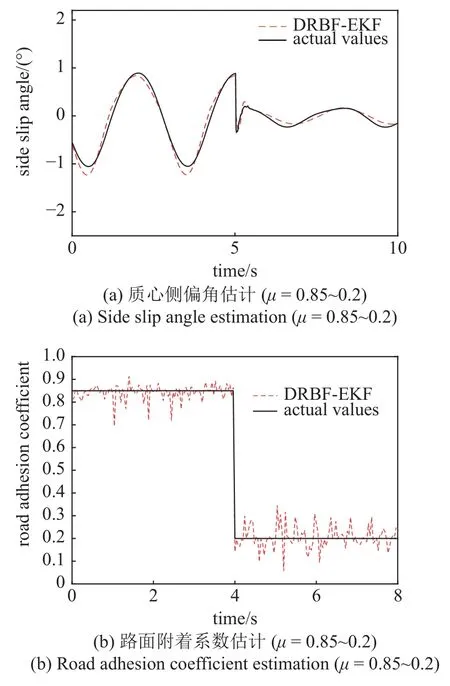
图7 由干燥柏油路至冰路面质心侧偏角和路面附着系数联合估计Fig.7 Joint estimation of sideslip angle and road adhesion coefficient from dry asphalt road to ice road

由图6 可以看出,60 km/h 对接路面,在由冰路面到干燥柏油路对接路面时,由于工况的变化质心侧偏角估计出现较大误差,在0.8 秒后恢复,能够对实际值进行快速调整和有效跟踪.图7 由干燥柏油路到冰路面时,质心侧偏角估计没有出现这种情况.在路面附着系数估计时,由于工况复杂度增加,比单一路面估计误差增大,但是最大误差小于0.18,能够稳定在实际值附近.

工况二:车速90 km/h 对接路面,质心侧偏角和路面附着系数联合估计结果如图8、图9 及表6所示.

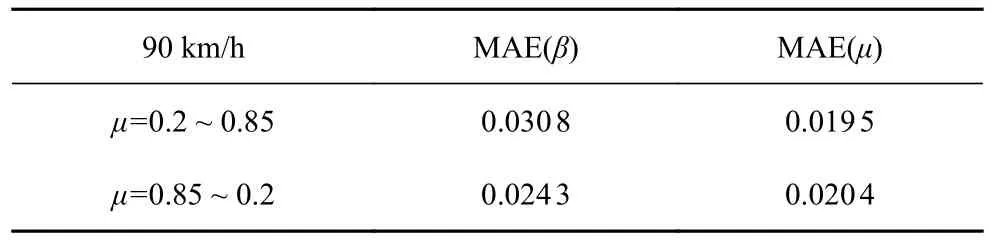
表6 车速90 km/h 对接路面估计误差Table 6 Error of vehicle speed 90 km/h on joint road

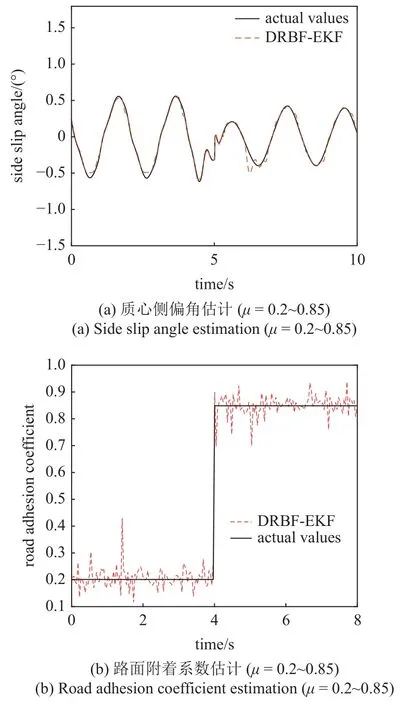
图8 由冰路面至干燥柏油路质心侧偏角和路面附着系数联合估计Fig.8 Joint estimation of sideslip angle and road adhesion coefficient from ice road to dry asphalt road

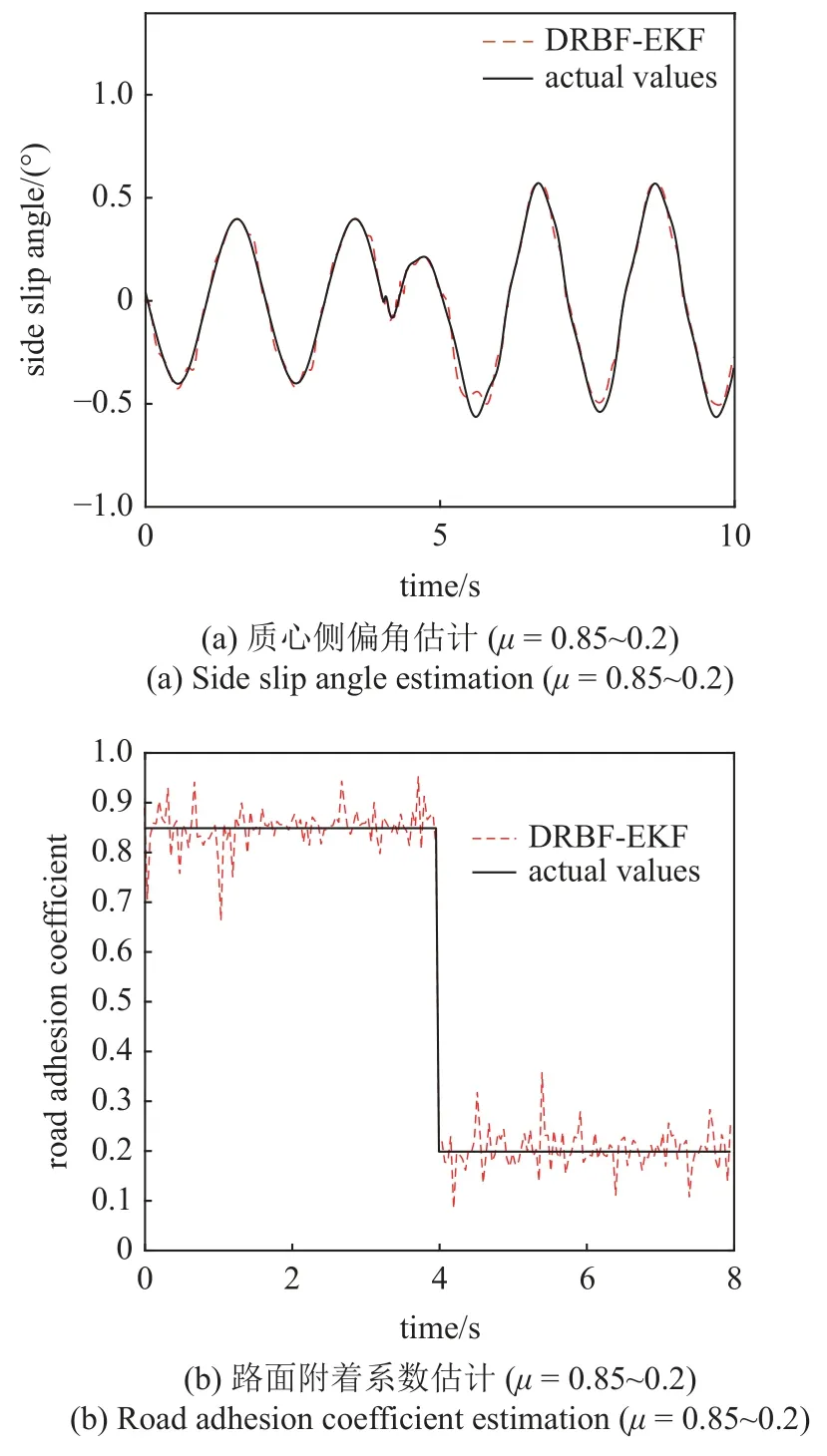
图9 由干燥柏油路至冰路面质心侧偏角和路面附着系数联合估计Fig.9 Joint estimation of sideslip angle and road adhesion coefficient from dry asphalt road to ice road

由图8、图9 及表6 可以看出,在对接路面上由于路面特性发生变化,对算法的自适应性提出更高要求.所提出DRBF-EKF 算法在质心侧偏角和路面附着系数估计时,质心侧偏角和路面附着系数平均绝对误差最大值为0.030 8,在不同车速下都能够自适应地稳定在测试值附近.

3.2 实车实验

实验车辆采用4WID 纯电全线控沙滩车(UTV),由轮毂电机内置WSS 传感器可测得四个车轮转速和转角,通过CAN 总线传输到电脑端,车载惯性导航IMU 型号为MTI-G-710,采样周期为2.5 ms.实验车辆、传感器及数据采集设备如图10所示.

图10 实验车辆和传感器设备Fig.10 Vehicle and sensors equipment for the experiment

由于实车实验测得的数据量巨大,10 秒内得到轮毂电机传感器数据3932 组,惯导数据13 706 组.为了得到一个计算快捷的轻量化模型,在进行时间戳电脑时间对齐后,对所测数据均匀取400 个样本进行训练和测试.轮毂电机内置传感器如图11(a)和图11(b)所示,惯导测得的数据如图11(c)和图11(d)所示.

图11 轮毂电机内置传感器和惯导测得数据Fig.11 In-wheel motor sensors and IMU measurement data

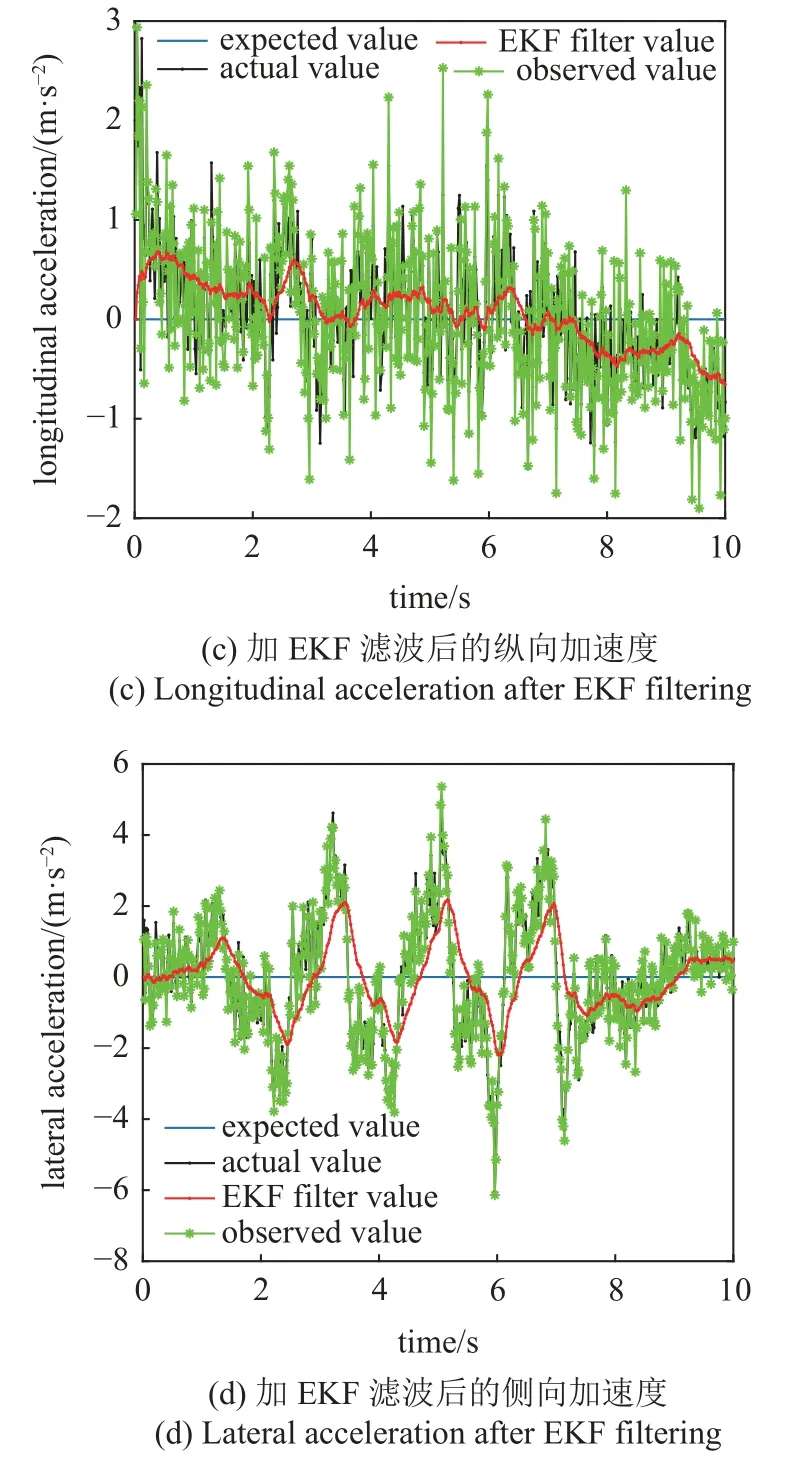
图11 轮毂电机内置传感器和惯导测得数据 (续)Fig.11 In-wheel motor sensors and IMU measurement data (continued)

由图11 可以看出,实验车辆在低速条件下转弯时方向盘出现抖动,导致左前轮转角在转弯时所测数据不光滑.纵向加速度、侧向加速度由惯性导航单元测出,所得噪声较大,由EKF 滤波去除噪声后得到的估计值较为平稳.

采用本文所提出的算法,进行质心侧偏角和路面附着系数联合估计,结果如图12 所示,DRBFEKF 联合隐含层神经元个数和估计误差的关系如图13 所示,DRBF-EKF 和DRBF 估计质心侧偏角误差见表7.

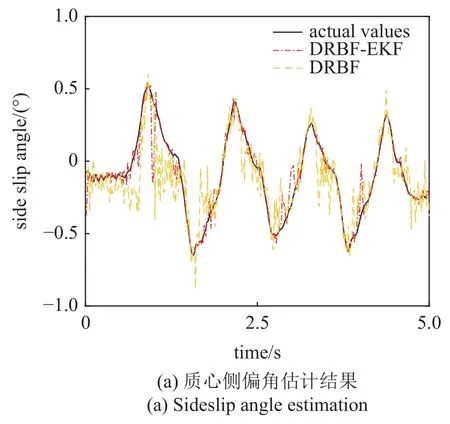
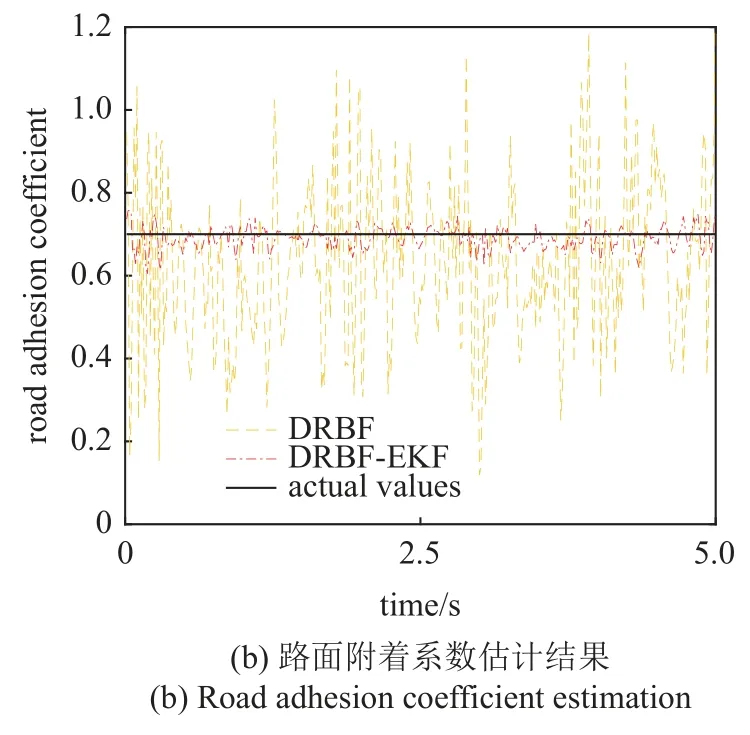
图12 DRBF-EKF 质心侧偏角和路面附着系数联合估计Fig.12 DRBF-EKF sideslip angle and road adhesion coefficient joint estimation

图13 DRBF-EKF 估计精度与隐含层神经元个数关系Fig.13 The relationship between DRBF-EKF estimation accuracy and the number of hidden layer neurons

由图12 和图13 和表7 可知:(1)在加入EKF滤波之后,DRBF-EKF 方法可以消除方向盘转角的抖动,对质心侧偏角和路面附着系数估计结果几乎没有影响;(2)所提出的DRBF-EKF 方法在质心侧偏角估计时具有较高的估计精度,平均绝对误差为0.036 7°,小于没有加EKF 滤波的DRBF 估计误差0.116 2°,精度提高了68%,与惯性导航单元测得的实际值保持较好的一致性;(3)在路面附着系数估计时,增加EKF 滤波后,DRBF-EKF 估计精度提高了79%,估计值稳定在0.7 左右;(4)DRBF-EKF 方法在估计时,随着隐含层神经元个数的增加,估计精度提高,但同样会增加计算复杂度,延长算法运行时间.在质心侧偏角估计时,隐含层神经元个数75 和140 时的误差差别不大.综合考虑,在质心侧偏角估计时,隐含层神经元个数75 时为最优解,同样路面附着系数估计时,隐含层神经元个数取62 最优.

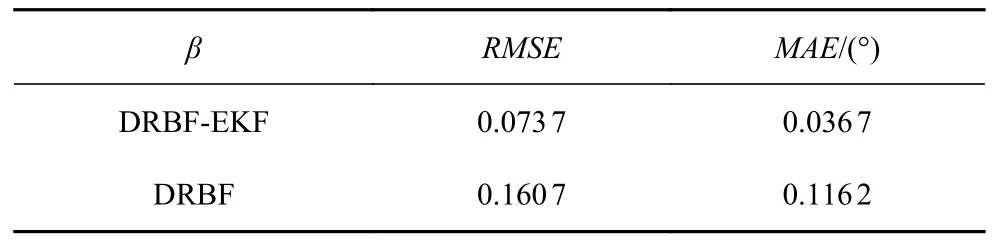
表7 DRBF-EKF 和DRBF 质心侧偏角估计误差结果对比Table 7 The error between DRBF-EKF and DRBF sideslip angle estimation

4 结论

本文针对分布式驱动电动汽车在质心侧偏角和路面附着系数估计过程中,估计精度和实时性不能同时满足的问题,利用现有传感器,提出了一种结合PCA 多元统计分析、扩展卡尔曼滤波、K-means 算法改进的RBF 神经网络车辆质心侧偏角和路面附着系数动态联合估计器.通过仿真和实车实验验证了该算法的有效性,得到主要结论如下.

(1)所设计的DRBF-EKF 动态联合估计器实时性和估计精度均优于扩展卡尔曼滤波算法,算法架构简单,运行速度快,在不同车速和路面特性变化时也表现出较强的鲁棒性,因此该算法具有良好的工程应用前景.

(2)DRBF-EKF 估计方法与DRBF 方法相比,显著提高了估计精度,其中,质心侧偏角估计精度提高了68%,路面附着系数估计精度提高了79%.

(3)分析了DRBF-EKF 估计方法在质心侧偏角和路面附着系数联合估计时,可以同时满足估计精度和实时性要求的最佳隐含层神经元个数,研究思路和结果可为相关研究提供参考.