基于有限元方法的换热器内部管路传热特性分析

王 震* 刘惠军

（山东铁雄新沙能源有限公司）

0 引言

换热器是重要的热量传递装备，在能源化工、金属冶炼、动力工程等领域被广泛应用[1]。换热器的种类较多，体积、功能和造价等有着显著差异。管壳式换热器是化工反应中的重要设备，在石油冶炼行业被广泛应用，其数量约占换热器总数的75%以上。管壳式换热器的核心换热元件为换热管，其受到复杂的热力载荷作用，也是影响换热效率的关键元件[2]。目前，换热方面的研究方法包括现场测试、理论计算和数值仿真等[3]。在流体分析方面，数值仿真方案有着更好的应用价值与效果[4]。通过有限元分析得出的仿真数据误差较低，能够满足绝大多数工程需要[5]。为此，基于Fluent 软件对换热器内管路流场特性进行研究，通过仿真结果进行分析，定性地判断换热器的性能。此外，由于热载荷具有循环性，因此需要对换热管结构进行模态分析，根据激振频率下的振型结果，有效地衡量整个结构设计的合理性。

1 流场基本控制方程与定解条件

1.1 流体能量方程

基于节点理论的动量定理，可得出以下结论：在换热器内部流体表面，承受的外力合力与节点之间流体转移过程中单位时间上的动量变化量相匹配。节点理论主要将流体分为微单元进行计算，而流体相邻单元之间的黏性阻力可进行二次分解。因此，在二维坐标系oxy条件下，可将换热管外缘流体的动量方程表示为：

1.2 定解条件

换热特性的求解关键在于能量方程，需要给定换热边界条件，即定解条件。对于传热控制方程中难以求解的为动量方程，目前尚未没有完全求解的方法，均采用近似模型方法进行研究。有限元计算中的定解条件是指边界上的物理参数，包括流速、压力以及热流载荷等。根据传热介质的能量方程表达式形式可知，该偏微分方程具有封闭性，结合动量方程和质量连续方程，理论上可以完成相关的参数的求解。但是，动量方程自身具有显著的非线性效应，通过理论推导直接进行计算存在较大难度。目前，主流的研究方案为相似理论和实验模型，否则难以得出求解结果。对于传热过程而言，可在动量方程的基础上，引入边界层理论，从而在局域范围内简化模型的同时确保计算精度，具有较好的工程意义。

1.3 边界层分析

边界层理论最早由西方国家研究得出，其针对对流换热过程，将控制方程进行了转换，满足不同边界条件下的求解要求。根据边界层理论可知，换热器内的流体介质在热传递的过程中，可分为边界层和主流层两个区域。其中，边界层内流体具有更显著的黏性效应，因此传热流体在切向方向的流速和压力具有一定的梯度特性。而对于主流层，流体的黏性效应几乎不再影响其动力参数，因此可将其视为理想状态。边界层之前的流体速度即为主流区流速u∞，一般工程上将主流区流速的99%位置作为边界层的基本划分界限。边界层在二维坐标系oxy下的基本结构组成如图1 所示，根据湍动特点又可以分为层流层（宽度为xc）、过渡层和湍流层。在厚度方向上，又可以分为层流底层（厚度为δ）和缓冲层（厚度为δ′）。在层流层内，传热方程满足特定的规律和控制方程，因此，可有效地简化动量方程。在流体分析软件中，集成了专业的边界层算法处理器，能够有效地确保精度和可靠性。

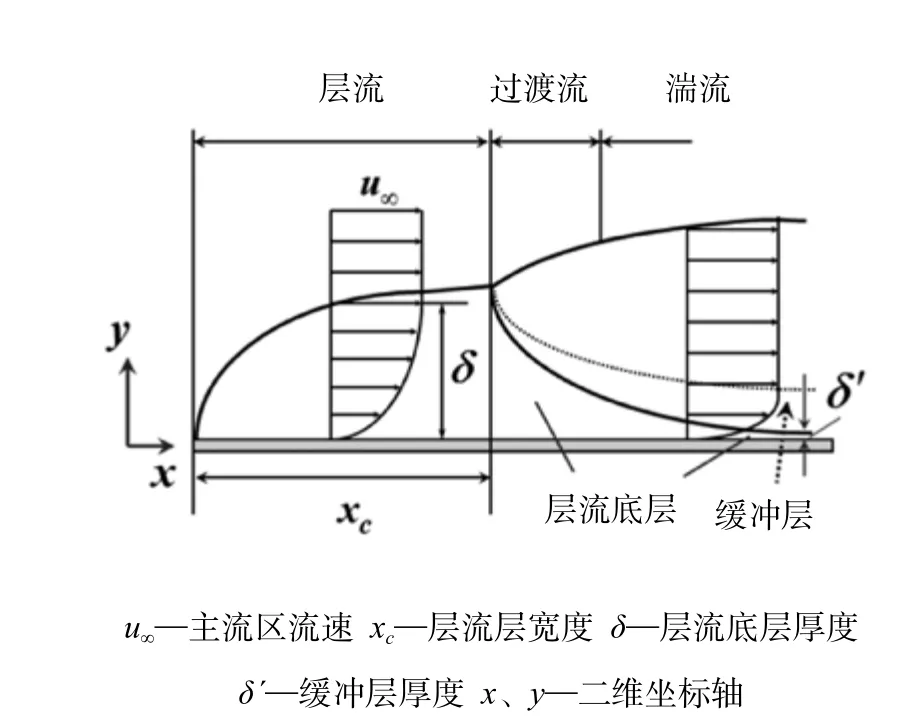
图1 边界层主体结构

2 换热管传热特性分析

2.1 管路模型的建立与网格划分

换热器内部的换热效果受很多因素影响，在机械结构方面，换热管和折流板尺寸均能造成流场发生突变效应。因此，在管路模型中建立单管模型，并考虑折流板对流场的影响效果。通过三维建模软件UG 将模型导入ANSYS 软件中，得出固体模型结构，如图2 所示。通过布尔运算转换为流体模型，其中，L1和L2分别为折流板左侧和右侧距离换热管轴线的距离，θ为换热管轴线与折流板端面的夹角。

图2 换热管结构模型

导入后的模型需要进行网格划分和相关参数定义。其中，网格的划分质量对于模型的计算精度和效率有着关键的影响。边界层处理方法有两种：壁面函数法和近壁模型法。近壁模型法对于网格的密度要求较高，即在网格层面上区分边界层与主流层。由于换热管轴向尺寸较大，因此，文中优选壁面函数法进行传热计算，在求解器中考虑流体交互效应。在Gambit 软件内将模型进行分段和网格划分，得出网格形状和疏密程度，如图3 所示。在壁面函数法条件下，需要校验第一层网格尺寸，因此需要局部加密，并确保网格的畸变程度处于较低的水平，在二维平面内分析传热介质的速度场和压力场。

图3 网格划分结果

2.2 结果分析

通过连续的迭代计算，能够得出换热管流体模型的稳态速度场、压力场和温度场，如图4 所示。从图4 可以看出：换热器内的流体介质在换热管和折流板作用下，流速呈现局部降低趋势，分布具有不连续性，两侧的速率大小差异较大，速度梯度较为显著；压力分布与速度分布呈现出明显的区别，压力具有双侧对称的特点，在流速同向一侧形成多环状结构，压力的差异性较小，梯度不明显；从温度场分布可以看出，该换热管对于温度的控制效果良好，未出现局部温度过高问题。

图4 流场分析结果

3 换热管模态分析

3.1 模态分析原理

在长期工作条件下，换热器内传热介质的流体运动对于机械结构的疲劳损伤不可忽略，因此，需要对结构刚度和模态响应进行分析和研究。模态分析能够有效地弥补静态结构设计的不足，在动态载荷条件下判定结构的稳定性和可靠性，是性能优化的重要技术手段。从本质上分析，模态计算是一种结构动力学研究方法[6]，能够对换热管和折流板结构进行激振频率下的动态模拟。模态特性对应的研究目标为固有频率和振型，其中，固有频率是所有机械结构的固有属性，理论上来说有无数个，但是实际工况下的激振频率是有限的。振型是指特定固有频率下的振幅响应，并能够基于振型仿真结果对机械结构进行改善。目前，随着有限元技术的发展和进步，模态仿真的结果与试验结果已经相差无几，在各个行业和领域有着广泛的应用。

3.2 振型分析

通过UG 软件建立换热管和折流板模型，导入ANSYS Workbench 模块中进行模态计算。由于换热管在换热器内部为固定状态，因此，模态分析类型选用自由模态，即忽略前六阶的无效固频，将第七阶模态作为有效分析结果。有效模态结果中的前两阶振型如图5 所示。根据计算结果可知：第一阶固有频率为11.5 Hz，在该激振频率下，折流板端面容易发生较大位移，最大位移分布呈团状；第二阶固有频率为28.2 Hz，最大振幅分布呈条状，对于冲击力的抵抗性能较好。在模态分析中，振型中的位移为相对位移，并非激振下的实际位移。

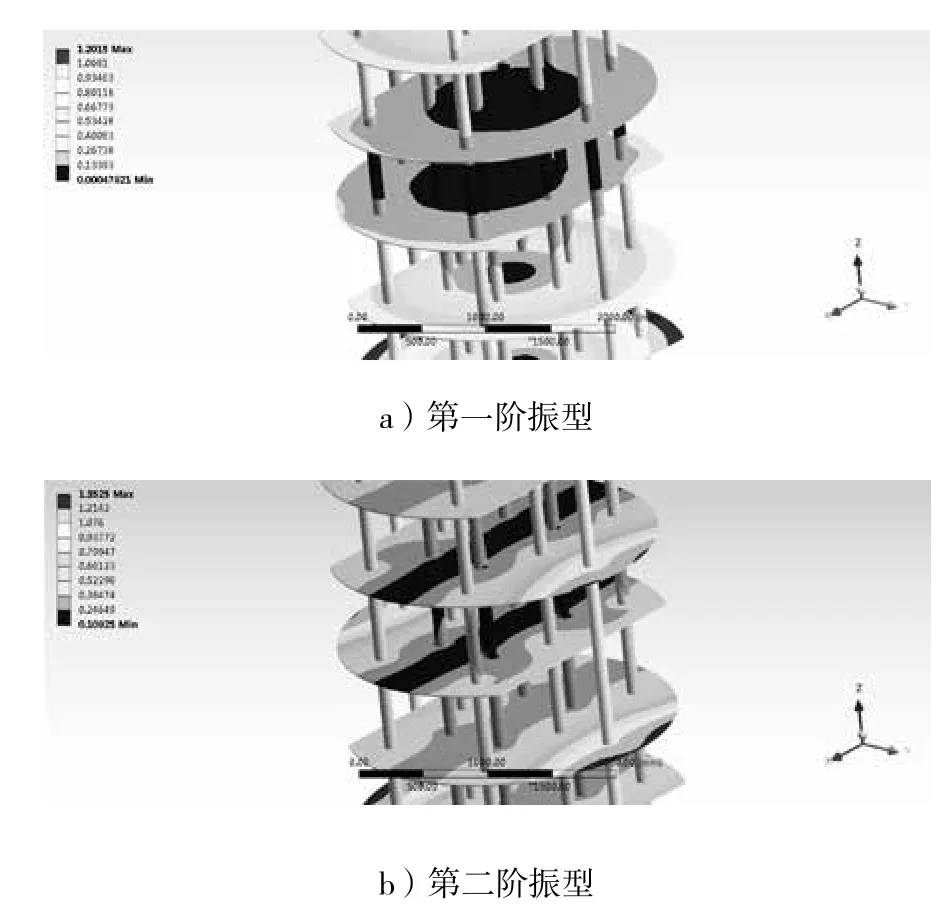
图5 振型分析结果

4 结论

换热器是重要的过程装备，其传热特性对于整个流程的生产效率有着重要的影响。采用试验方法进行传热特性的研究，不但成本较高，而且难以获得传热因素的影响效果。基于有限元方法，建立传热管流体模型，通过对速度场、压力场和温度场进行分析，验证了换热器内部流体介质的稳定性。

通过换热管和折流板整体结构的模态分析，得出刚度薄弱结构，能够为后续的结构优化提供重要的依据。在换热器内部，换热管路为单通密闭式结构，能够有效地隔开冷介质与热介质。不同介质之间的传热主要依赖于管壁外缘的流场动态特性，即换热器的换热性能。在工程中，换热系数和压降是换热管的核心性能参数。从数值上分析，当换热管的换热系数和压降的比例提升时，能够证明该设备的换热性能随之提升。因此，需要确保该比值处于较高的范围，可根据换热器内部结构特点，采用流体能量方程表达不同介质之间的换热状态。