基于亥姆霍兹自由能的实际气体状态方程

齐 超* 刘 拓,2 易满满

（1.西安航天动力研究所 2.西安航天远征流体控制股份有限公司 3.北京电子工程总体研究所）

0 引言

氮气是石油、化工、航空航天等行业的常用气体。石化工业中氮气广泛应用于油田钻井、采油、作业等工序；航空航天工业中氮气广泛用于挤压驱动液体火箭推进剂，或作为工质通过喷管直接流动产生推力等[1-2]。氮气的物性（包括温度、压力、密度、黏度、比热容、焓、熵等）是上述工业系统设计的重要基础。

气体状态方程是用来描述气体物性的函数关系，通过两个独立变量，可以推导计算出其余物性参数。气体状态方程包括理想气体状态方程和实际气体状态方程。本文对四种常用的气体状态方程：理想气体方程、范德瓦尔斯方程、Redlich-Kwong 方程以及基于亥姆霍兹自由能的Span 方程，进行了描述和分析。最后以美国国家标准与技术研究院（NIST）的氮气物性数据为标准，对上述四种状态方程进行了对比中分析。

1 氮气基本性质

氮气的基本性质如表1 所示。气体状态方程中的系数往往需要通过表1 中的分子量、临界温度、临界压力、临界密度等参数计算。

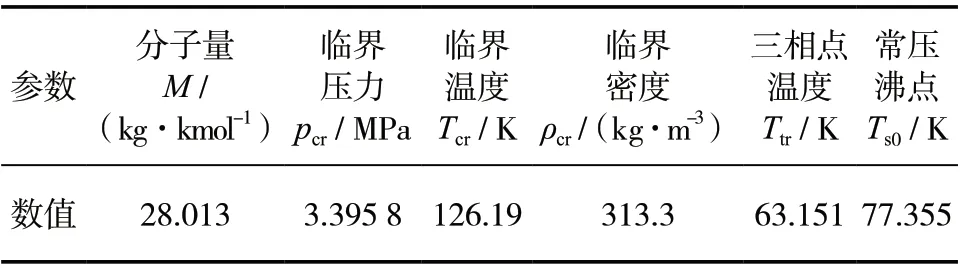
表1 氮气基本性质

2 气体状态方程

2.1 理想气体状态方程

理想气体是一种理想模型，假设气体分子本身不占有体积且分子间无相互作用力。实际应用中往往把压力较低的气体近似看作理想气体[3]。由于理想气体的特性，气体密度与气体温度、压力呈现简单线性关系，理想气体状态方程如式（1）所示：

2.2 范德瓦尔斯气体状态方程

范德瓦尔斯对理想气体状态方程式进行了修正，提出了考虑了实际气体分子本身的体积以及分子间的相互作用力的影响的实际气体状态方程——范德瓦尔斯方程。范德瓦尔斯方程如式（2）所示：

对于氮气工质，通过式（3）可以得到范德瓦尔斯方程中的a、b值，计算后可得常数a、b分别为174.3 m6·Pa/kg2、0.001 38 m3/kg。

2.3 Redlich-Kwong气体状态方程

在范德瓦尔斯方程的基础上，Redlich 和Kwong通过对内压力项的修正，提出了含有两个常数的R-K方程，保留了范德瓦尔斯方程的简单形式，提高了计算精度[4-5]。R-K 方程如式（4）所示：

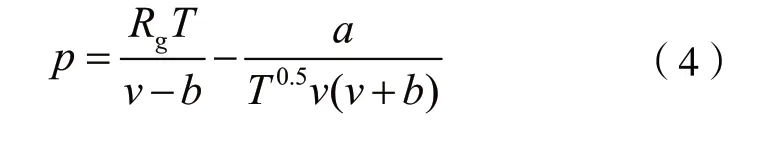
与范德瓦尔斯方程类似，系数a考虑分子之间吸引力，与气体本身性质有关，单位为m6·Pa·K0.5/kg2；系数b考虑了分子本身有体积，也与气体本身性质有关，单位为m3/kg；a、b可通过式（5）计算：

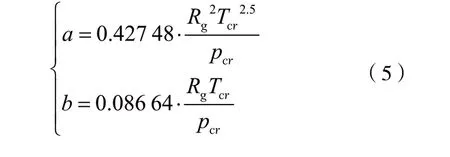
对于氮气工质，通过式（5）计算可得R-K 方程中的a、b分别为1 983.6 m6·Pa·K0.5/kg2、0.000 956 m3/kg。

从式（2）和式（4）可以看出， R-K 方程与范德瓦尔斯方程的形式类似，均可展开为比体积的三次方程式，因此二者往往也称为立方型方程。

2.4 Span气体状态方程

与上述理想气体状态方程和基于理想气体状态方程修正的立方型方程不同，通过能量方程利用偏离函数思想推导出亥姆霍兹自由能状态方程，改变了以往的计算方法，计算范围广且精度更高[6]。

亥姆霍兹自由能A表示成两个独立变量密度ρ和温度T的函数，即：

通过式（10）和表2 中的系数即可进行三参数（温度、压力、密度）的迭代求解。

表2 Span状态方程系数

3 状态方程比较

以美国国家标准与技术研究院（NIST）的氮气物性数据为标准，对上述4 种状态方程的计算精度进行对比。工质为氮气，温度分别为200 K、300 K、400 K 和500 K；压力为0.1～50 MPa，各工况下NIST数据和各状态方程的计算结果如图1 所示。

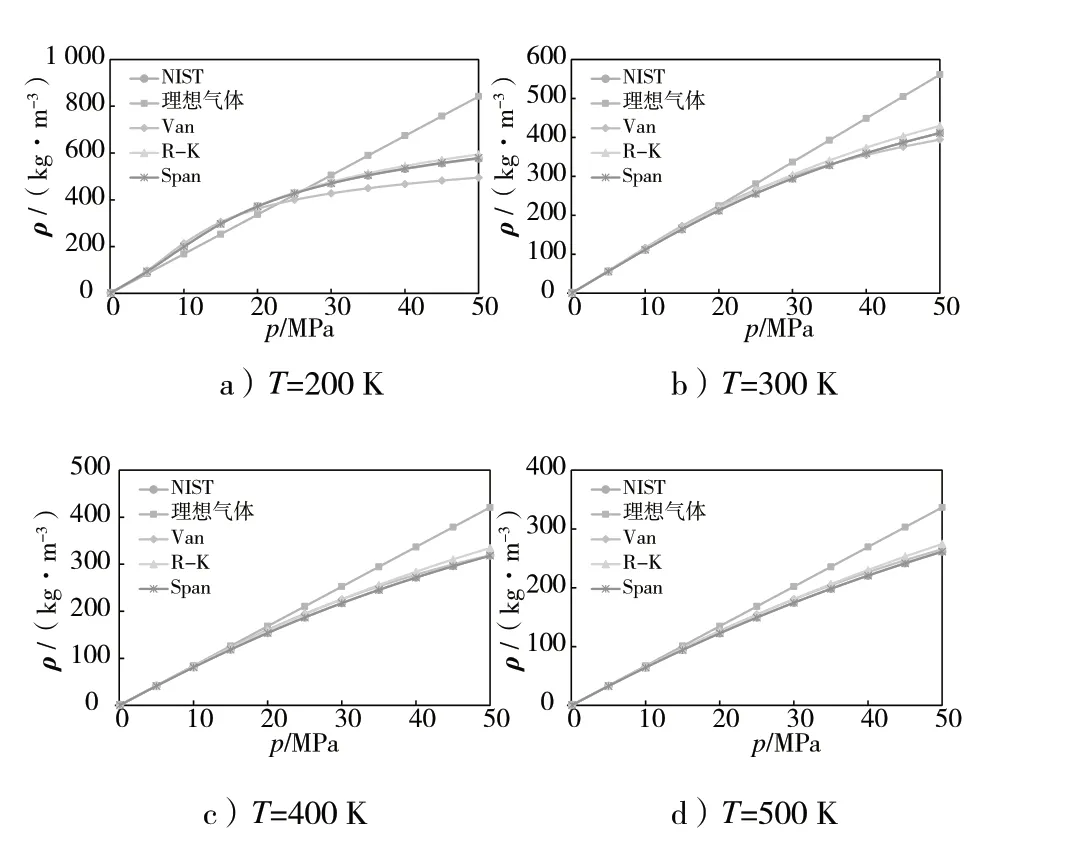
图1 密度计算结果对比

从图1 可以看出，理想气体状态方程计算的密度与压力始终呈线性关系。200 K 温度下，随着压力不断提高，气体的非理想性越来越显著，范德瓦尔斯方程（Van）、R-K 方程（R-K）以及Span 方程（Span）计算得到的氮气密度随着压力的增加逐渐放缓，其中范德瓦尔斯方程计算的密度最小，且与其余两个方程存在一定差异；Span 方程的计算结果与NIST 数据非常接近，R-K 方程的计算结果介于范德瓦尔斯方程与Span 方程之间。随着温度升高，三种实际气体状态方程的计算结果逐渐趋同，且均与NIST 数据较为接近，同时由于介质状态接近理想气体，理想气体状态方程计算的偏差也逐渐减小。

理想气体状态方程、范德瓦尔斯方程、R-K 方程以及Span 方程计算结果与NIST 数据更直观的偏差如图2 所示。图2 中横轴为NIST 数据，纵轴为各方程在相同工况下的计算结果。密度较小时，各方程的计算结果与NIST 数据非常接近；密度较大时，理想气体状态方程的偏差越来越大，范德瓦尔斯方程的偏差也逐渐扩大到10%以上，Span 方程与NIST 结果一致性很好，基本落在等值线上，R-K 方程的偏差介于范德瓦尔斯方程与Span 方程之间。事实上，密度越小，气体越接近理想气体状态，各方程的计算偏差越小；密度越大，气体非理想性越显著，计算结果偏差越大。

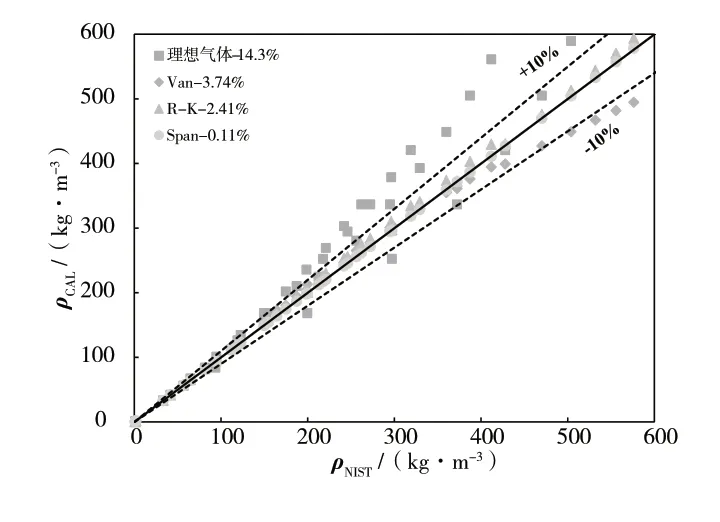
图2 密度计算结果偏差

如上所述，理想气体状态方程与NIST 数据存在较大偏差，三种实际气体状态方程的计算结果与标准数据较为接近，为了更清晰地比较三种实际气体状态方程的计算精度，给出了范德瓦尔斯方程、R-K 方程以及Span 方程在不同工况下的计算偏差，如图3所示。图3 中横轴为NIST 数据，纵轴为各方程在相同工况下的计算偏差。从图3 可以看出，密度较小时（＜400 kg/m3），范德瓦尔斯方程与R-K 方程的计算偏差较为接近，计算偏差基本都能控制在5%以内；密度较大时（≥400 kg/m3），R-K 方程依然保持了相对较好的计算精度，而范德瓦尔斯方程的计算结果出现了较大偏差，相对偏差达到10%以上。Span 方程的计算偏差基本都落在x轴上，意味着在全工况范围内Span 方程的计算偏差非常小，都能控制在0.5%以内。综上可知，Span 方程的计算精度远高于另外两种立方型方程。

图3 三种实际气体状态方程计算偏差

表3 所示为各方程的计算结果统计。统计结果与上述分析一致，基于亥姆霍兹自由能的Span 方程计算精度最高，平均偏差为0.11%，R-K 方程和范德瓦尔斯方程次之，平均偏差分别为2.41%、3.74%，理想气体状态方程偏差最大，为14.3%。

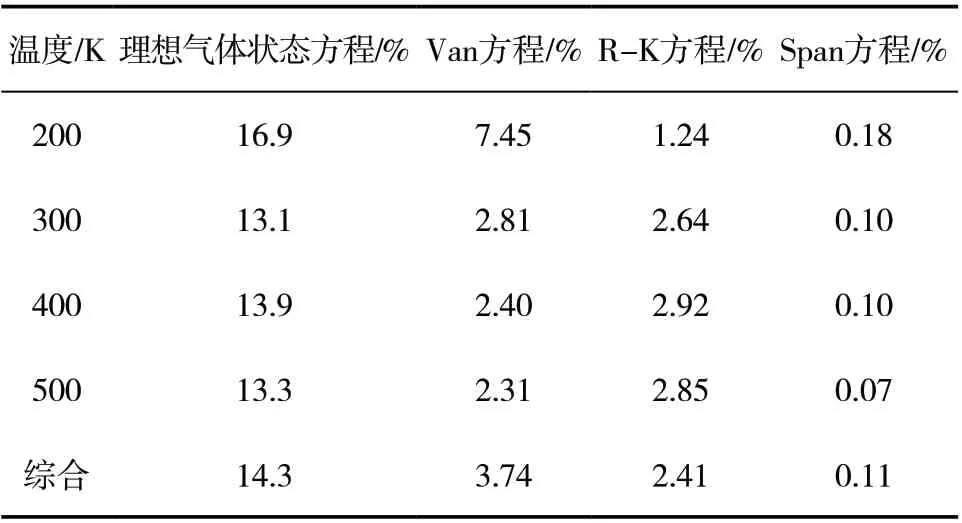
表3 计算结果偏差统计

综上所述，当气体温度较高、压力较低时，气体分子间距较大，分子之间的作用力较小，介质接近理想气体状态，四种状态方程的计算结果偏差较小；温度越低、压力越高时，气体非理想性逐渐显著，理想气体状态方程和立方型方程存在一定偏差。基于亥姆霍兹自由能的Span 方程在各工况下都展现出了较好的计算精度。

4 结论

本文对理想气体状态方程、范德瓦尔斯气体状态方程、R-K 气体状态方程以及基于亥姆霍兹自由能的Span 气体状态方程进行了介绍。通过上述四种状态方程计算了氮气在200～500 K、0.1～50.0 MPa 工况下的密度。以NIST 的氮气物性数据为标准，对上述几种状态方程进行了比较，结果表明Span 方程的计算结果和标准值吻合最好，平均偏差为0.11%，远小于理想气体状态方程和立方型气体状态方程，可以用于氮气物性的精确计算。