循环制动工况下货车车轮疲劳强度研究

刘思达，付茂海，徐德山，张家梁

(西南交通大学 机械工程学院，四川 成都 610031)

0 引言

川藏铁路是我国第二条进藏铁路，其中雅安至林芝段线路最复杂，地形陡度起伏最大，更有从海拔500 m四川盆地区域急剧爬升至海拔4 500 m的川西高原地区。线路规划上，在火夹仲至泸定段，从坡顶行至泸定时，若不考虑在康定停车，则有一段坡度约为-30‰、长约80 km的长大下坡道，这对列车的制动性能和车轮的安全问题提出了更高的要求。

虽然车辆速度和载重不断提升，但踏面制动仍是我国货车的主要制动方式。在川藏铁路上运行的列车，车轮不仅要承受长大下坡道循环制动过程中由于踏面制动产生的热负荷，还有由于轨道的曲线性、不平顺性产生的动载荷及轮轴组装时由于过盈配合产生的压装应力，因此对川藏铁路上货车车轮疲劳强度的分析就显得尤其重要。针对车轮辐板疲劳问题，Seo等[1]采用UIC标准和多轴疲劳准则中的Dang Van法则评价车轮辐板的疲劳强度。刘雅玲等[2]建立了1/2车轮车轴模型，参照TB/T 3463-2016，在机械载荷和热负荷共同作用下对车轮静强度和疲劳强度进行了校核。

上述文献采用了不同的疲劳强度准则对车轮疲劳强度进行校核，但对车轮在循环制动下的疲劳强度鲜有分析，故本文以川藏铁路为研究背景，首先选取不同坡度下的长大下坡道进行车轮的循环制动计算，然后采用TB/T 3463-2016[3]对此线路上运行的货车的车轮辐板进行疲劳分析及评定。

1 长大下坡道循环制动工况计算

循环制动是货物列车在长大下坡道运行时电制动力不足情况下采用的一种安全制动策略。列车在采取周期性制动时，坡道下滑力大于基本阻力与电制动力之和，仅依靠电制动力无法使列车速度降低，需要周期性地施加空气制动以控制车速，可将该过程列车运动进行数学化表述，将列车视为刚性点，列车运动学方程表示为：

dvdt=Gi-Bd(v)-Bk(r,v)-w0(v)M.

(1)

dxdt=v.

(2)

v(t)≤vX.

(3)

tz≥tc+tk.

(4)

其中：v和x分别为列车运行速度及运行里程；Gi为列车在坡度i上的下滑力；Bd(v)为速度v时机车的最大电制动力；r为减压量；Bk(r,v)为减压量r、速度v时的空气制动力；w0(v)为列车基本阻力；M为列车总质量；vX为制动限速；tz为列车从缓解速增至制动限速过程中的增速时间；tc和tk分别为再充风时间及空走时间，按照TB/T 1470.1-2018《列车牵引计算规程》[4]取值。

根据川藏线的基本情况,列车编组形式选取为HXD1(本务机车)+HXD1(重联机车)+22辆C70E型敞车，牵引重量为2 070.2 t，列车总重为2 470.2 t。在-30‰坡度下，列车下滑力为727 kN，而一台机车能提供的最大电制动力为461 kN，故当两台机车电制动正常时无需使用空气制动，因此本文计算在一台机车电制动失效时，在干燥轨面行驶的列车的循环制动特性。以紧急制动距离1 400 m计算坡道限速，对制动管主压力为500 kPa的列车行驶在坡度-24‰、长度90 km以及坡度-30‰、长度80 km两种长大下坡道下做循环制动计算，计算结果如图1所示。

图1 列车循环制动曲线

在制动计算时，一台机车全程施加电制动力，两种线路施加空气制动减压量都为50 kPa，每块闸瓦压力为4.007 kN。由图1可知：在-24‰坡度、90 km长大下坡下列车通过时间为4 500 s，制动限速为78 km/h，在一个循环内列车制动时间为5 s，缓解时间为21 s；在-30‰坡度、80 km长大下坡下列车通过时间为4 684 s，制动限速为68 km/h，在一个循环内列车制动时间为35 s，缓解时间为21 s。

2 长大下坡道循环制动下车轮的温度场分析

车轮选取为HESA型车轮，车轮滚动圆直径为840 mm，踏面类型为LM型，辐板为S型，轴重为25 t。车轮材料为CL60钢，材料密度为7 833 kg/m3，其他材料参数如表1所示，对流换热系数按TB/T 3463-2016的推荐取22.713 W/(m2·℃)，环境温度为24 ℃。

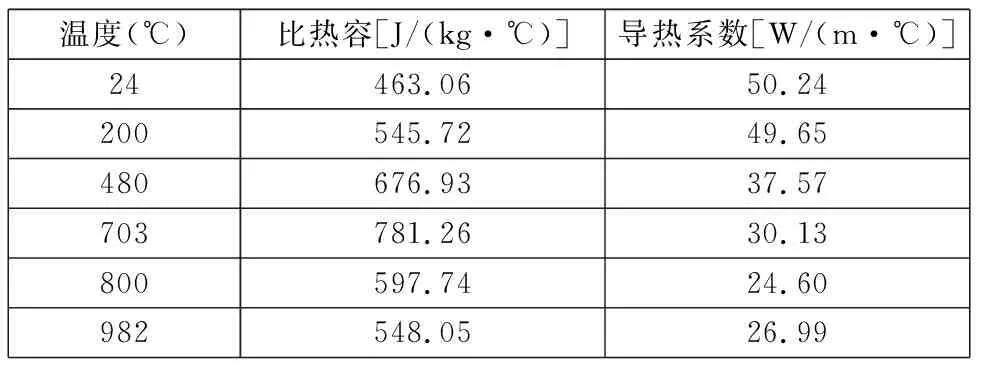
表1 车轮材料热学属性

在温度场计算时，将车轮踏面与闸瓦作用产生的热流密度作为第二类边界条件，将车轮的外表面与周围环境的对流换热作为第三类边界条件，将对称面作为绝热面；将热流密度简化为沿车轮踏面均匀分布[5]，作用于车轮踏面中心宽约85 mm。计算得到两种坡度循环制动下的车轮最高温度时间历程，如图2所示。

图2 车轮循环制动温度场特性

图2分析结果表明：制动主管压力为500 kPa的列车运行在坡度为-24‰和-30‰的线路上时，车轮最高温度分别为203.09 ℃和440.52 ℃；车轮最高温度随运行里程的增加而增大；当车辆运行在坡道末段时，车轮温度变化率略小于车辆运行在坡道起始段时的数值；车轮在一个循环内的最高温度呈现先上升后下降的状态，这与列车的速度运行变化基本一致，列车在减速过程中，速度降低使得车轮的摩擦热也相应减小，车轮温升速率也相应减小，当闸瓦离开车轮时，此时无热流的输入，车轮仅与周围空气进行对流换热，使车轮温度大幅减低。由于坡度的增加，列车的下滑分力也相应增加，在选定相同减压量的情况下，车轮的减速度降低且缓解时的加速度提高，使得列车的制动时间增多，在对流换热系数不变的情况下，车轮的热流输入时间增加，使得在更大坡度的车轮温升速率更高。

3 长大下坡道循环制动下车轮辐板疲劳强度分析

根据TB/T 3463-2016的规定，车轮的机械载荷包括轮轨垂向力、横向力和旋转角速度等部分，列车运行分为直线运行、曲线通过和道岔通过三种工况。在直线运行工况施加FZ1=0.625Pg；曲线通过工况施加FZ2=0.625Pg，FY2=0.35Pg；道岔工况施加FZ3=0.625Pg，FY3=0.21Pg。其中P为轴重，g为重力加速度。各工况的加载位置如图3所示。

图3 TB/T3463-2016各载荷在车轮上的作用位置

标准规定车轮疲劳强度采用主应力方向的应力变化量进行评定[6]。在车轮n个断面按照图示各载荷作用位置施加节点力，求解每个机械载荷工况与热载荷耦合下、转动过程中的车轮应力场，每个节点均可得到3n组应力张量。按照公式(5)～公式(8)计算各点的应力变化量Δσij：

Δσ11=σ11max-σ11min.

(5)

Δσ12=σ12max-σ12min.

(6)

Δσ21=σ21max-σ21min.

(7)

Δσ22=σ22max-σ22min.

(8)

其中：σ11max和σ22max为上述3n组应力张量中最大的σ1及σ2；σ11min和σ22min为上述3n组应力张量分别向σ11max及σ22max方向上投影的最小值；σ12max为σ11max所在工况下的最大σ2(若σ11max发生在曲线工况，则σ12max即为所有曲线工况的最大σ2)；σ21max为σ22max所在工况下的最大σ1(若σ22max发生在曲线工况，则σ21max即为所有曲线工况的最大σ1)；σ12min和σ21min分别为上述3n组应力张量分别向σ12max及σ21max方向上投影的最小值。

计算得到车轮辐板上各点的应力变化值Δσ应小于许用的应力变化值[Δσ]，计算结果如图4～图5所示。根据标准，由CL60钢制造的车轮辐板，其许用的应力变化值[Δσ]=360 MPa。

图4和图5的结果表明：在-24‰坡度下车轮辐板最大应力变化值出现在Δσ11与Δσ21，最大值为230.7 MPa，小于360 MPa，符合标准规定，四种应力变化的最大值位置均在车轮外侧辐板靠近轮毂圆弧段；在-30‰坡度下车轮辐板最大应力变化值为Δσ11，最大值为492.94 MPa，此外Δσ21、Δσ22最大值均大于360 MPa，超过了标准规定的许用值，其中Δσ11与Δσ21的最大值均在车轮内外侧辐板靠近轮辋圆弧段以及车轮内侧辐板靠近轮毂圆弧段，而Δσ12与Δσ22的最大值位置在车轮外侧辐板靠近轮毂圆弧段处。在不同坡度制动时车轮的温度不同，在两种温度下，车轮辐板应力变化最大值的位置发生了变化，在温度较低时，受轮轴间装配应力的影响大于温度的影响；当车轮温度较大时，辐板与靠近轮辋圆弧段处在温度的作用下产生了较大的热应力，从而影响了车轮辐板疲劳值的分布。由此可见，若车轮温度持续升高将对车轮的运行安全产生极大的危害。

图4 -24‰坡度下车轮辐板各点应力变化值

图5 -30‰坡度下车轮辐板各点应力变化值

4 结论

本文根据川藏铁路特点，对列车行驶在-24‰坡度、90 km和-30‰坡度、80 km长大下坡道进行制动计算，并对车轮在两种线路下的温度场特性进行了计算分析，最后根据TB/T 3463-2016对车轮辐板进行了疲劳强度评定，得出以下结论：在一台机车电制动失效的情况下，列车行驶在坡度更大的长大下坡道时，施加相同的减压量，列车在-30‰坡道的制动时间要大于-24‰坡道；车轮的最高温度随坡度的增加而升高，最高温度均出现在踏面处，-24‰坡道和-30‰坡道的最高温度分别为203.09 ℃和440.52 ℃；车轮辐板的应力变化值在-24‰坡道可以满足TB/T 3463-2016标准需求，而在-30‰坡道不能满足标准需求，且辐板易出现疲劳破坏的位置在车轮温度的影响下发生了变化。