谐波齿轮传动的传动误差建模与补偿

李 平，李静宇

(1.绵阳职业技术学院 智能制造学院，四川 绵阳 621000；2.沈阳农业大学，辽宁 沈阳 110000)

0 引言

因谐波齿轮传动兼具结构紧凑、零齿隙、高传动比、大扭矩、高响应及高传动精度等结构和运动学特性，故被广泛应用于高传动比减速装置、智能机器人、精密定位装置及航空航天等众多领域[1]。谐波齿轮传动系统一般由刚性内齿齿环(CS)、柔性薄壁外齿齿轮(FS)和椭圆形的波发生器(WG)三部分组成。

包含谐波齿轮传动的典型设备，通常以半闭环控制系统进行控制，即电机轴的转速或位置可以由电机轴上的传感器直接检测和控制，而负载端的转速或位置则由具有一定表观分辨率的传感器间接控制[2]。由于固有结构误差和FS的柔性，传动系统所固有的“角传动误差”就具有了非线性属性，因此在负载端则不能获得小于传感器表观分辨率的理想控制精度[3]。尽管谐波传动齿轮由于其零齿隙可以显著减少传动误差，但由于FS中的运动误差和非线性弹性变形引起的角传动误差仍然存在，就难免会导致半闭环控制系统的误差补偿能力下降[4]。

本研究将角传动误差分为同步分量和非线性弹性分量两部分，其中同步分量表现为与转动同步的周期性角传动误差，是由齿轮制造过程中固有的结构误差引起；非线性弹性分量表现为非线性弹性变形引起的具有滞后性的非线性现象[5]。同步分量通常可以被建模为传动系统转动角度的周期性振动，因此可以用基于模型的前馈方式来进行补偿[6]；而非线性弹性分量则通常被认为是机构中的弹性元件引起的无规则振动[7]。更重要的是，非线性弹性分量的非线性弹性属性可能会使半闭环控制系统的静态定位精度下降,特别是当负载角为几十到几百弧秒(1弧秒=1/3 600°)且要求精确定位的微位移区域，非线性弹性分量引起的负载端角传动稳态误差会使执行器不能精确定位[8]。与常规机械振动的动态行为不同，非线性弹性分量引起的静态定位精度下降现象现在尚未得到很好的研究。

在此背景下，本文提出了一种新的谐波齿轮角传动误差精确建模和补偿方法，以提高谐波齿轮传动系统的角传动精度和静态定位精度[9]。

1 角传动误差数学建模

谐波齿轮传动系统一般由刚性内齿齿环(CS)、柔性薄壁外齿齿轮(FS)和椭圆形的波发生器(WG)三部分组成，其中WG是在有长短轴的凸轮上套装柔性薄壁球轴承而成,谐波齿轮结构如图1所示。其传动原理为:WG的长轴两端支撑FS的两端外齿与CS的内齿啮合，随着WG转动，FS的长短轴位置发生变化，从而改变其与CS的啮合位置，最终实现大传动比减速。

谐波齿轮的角传动误差θTE通常由电机角位移θM、负载角位移θL及齿轮系数N三者通过下式表达：

θTE=θL-θMN.

(1)

为了提高模型的静态定位精度，故将角传动误差θTE定义为同步分量θSync和非线性弹性分量θHys的总和，并分别进行建模研究。

1.1 同步分量数学建模

同步分量θSync是由FS和CS齿的运动误差及齿轮和负载轴的装配误差引起，所以其与WG、FS和CS的相对转动同步[10]。通常认为θSync由电机角度的同步分量(θTEM)、FS与WG相对角度的同步分量(θTER)及负载角的同步分量(θTEL)三部分组成[11]。因为闭环检测系统无法直接检测负载角θTEL，且与θTEM相比，在同步分量建模中θTEL和θTER可以忽略不计，故只需用θTEM对θSync进行数学建模即可，因此同步分量的数学模型可表示为下式所示的周期性脉动:

θSync=∑nMi=1AM(i)cos[iθTEM+ΦM(i)].

(2)

其中：i为电机角度的谐波阶数,i=1,2,…,nM；AM为谐波幅度；ΦM为谐波相位。

图1 谐波齿轮结构

按式(2)对同步分量进行MATLAB建模分析，所得频谱如图2所示。图2中，传动误差波形由步进幅度为3.6°的电机轴顺时针运转一周的微调运动的电机角位移θM和负载角位移θL表示[12]。在AM(i)和ΦM(i)参数化中，提取了频谱幅度中的主要分量，如表1所示。

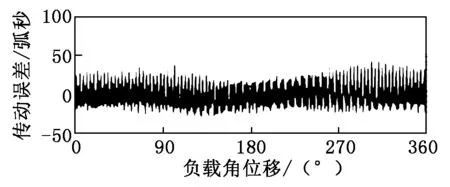
图2 同步分量的频谱分析图

表1 同步分量模型参数

1.2 非线性分量数学建模

为了准确仿真分析模拟谐波齿轮传动的非线性分量，所以在保证电机轴输出(0°～180°)±0.6°的正弦角度振幅的同时，提供0.05 Hz的超低频率，以消除惯性力和动态扭转共振的影响[13]。采用MATLAB按上述假设进行非线性分量数学建模所得分析结果如图3所示，图3(a)和图3(b)分别展示了顺时针方向(顺时针方向定义为负值，所以该正弦曲线的对称轴为-180°)电机轴输出转角和负载端传动误差在180°、45°和5°三个正弦角度振幅上随时间的变化曲线。由图3可知，在10 s、20 s、30 s三个速度反转点，3个正弦曲线振幅上的传动误差均约在0～80弧秒之间变化，且同步分量引起的振动分量仅叠加在了180°和45°的正弦角度振幅上，引起传动误差的波动，使其呈不规则波浪线状，而在5°这个正弦角度振幅上，所得传动误差曲线为接近平滑的样条曲线。

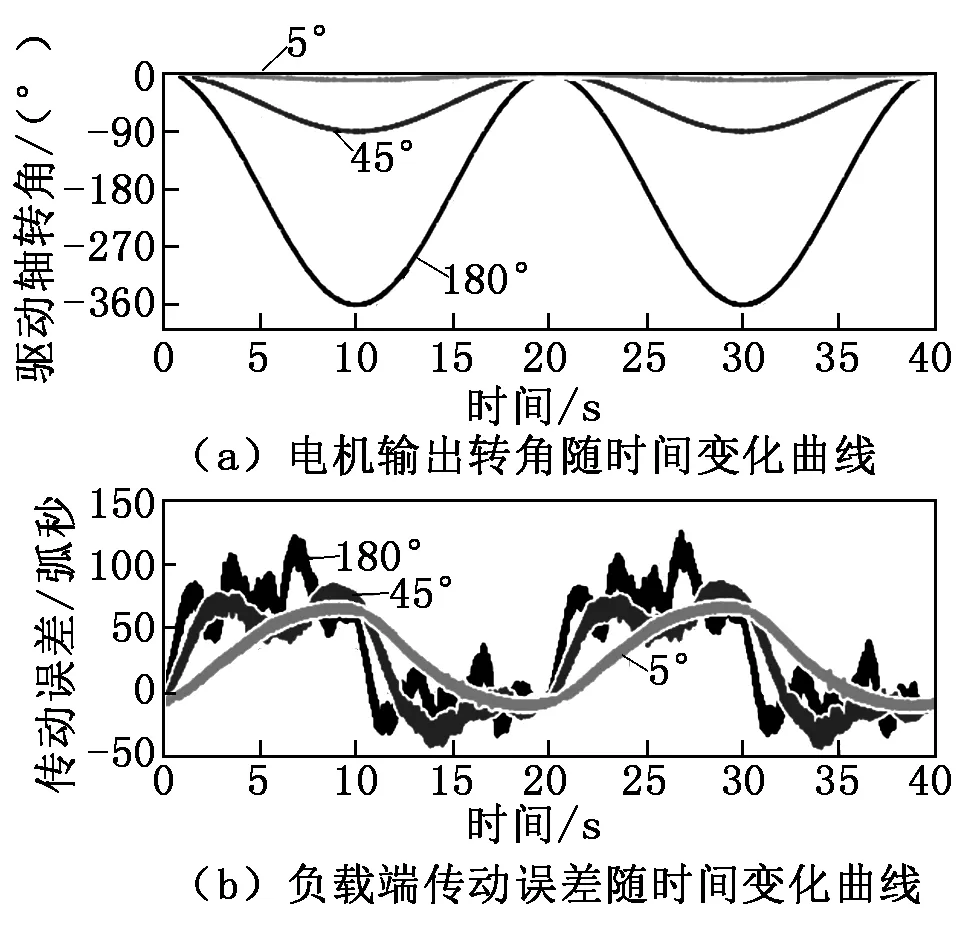
图3 电机轴输出转角和负载端传动误差变化曲线

同时对图3(b)负载端传动误差随时间变化曲线进行Lissajous变换，结果如图4所示，进一步证明了传动误差中的水平波动仅仅是非周期性滞后现象。同时由图4可推得：

(1) 传动误差的非线性弹性分量表现出具有非周期性的滞后特性，在大幅度运动中叠加到了电机角度的周期性同步分量上。

(2) 速度反转时迟滞曲线的倾斜角度是恒定的，与正弦角度振幅的大小无关。

图4 电机转角与负载端传动误差的Lissajous图形

这种非线性特征看起来与传动系统微位移区域中由弹性变形和滞后属性引起的滚动摩擦相似，因此，非线性弹性分量θHys在数学上可以由具有非线性弹性变形的滞后模型表示[14]。电机角位移θM和θHys的概念性非线性弹性变形的滞后模型如图5所示，其中δ为负载端的非线性弹性位移，θoffset为非稳定区的水平波动。由此可推得：

(1) 非线性弹性分量θHys随电机角位移θM变化。

(2) 存在非稳定区域θr，且该区域中的误差会随速度方向变化。

(3) 滞后行为发生在非稳定区域。

基于上述结论，非线性弹性分量θHys的数学模型可表示为速度反转后与负载端的非线性弹性位移δ相关的公式：

θHys=sgn(ωM)[2θoffsetg(ξ)-θ′Hys] |δ|<θrand|θHys|<θoffset

sgn(ωM)θoffset|δ|≥θror|θHys|≥θoffset.

(3)

且

g(ξ)=12-n[ξn-1-(n-1)ξ]n≠2ξ(1-lnξ)n=2.

(4)

δ=|θM-δ0|.

(5)

ξ=δθr.

(6)

其中：ωM为电机轴的角速度；sgn(ωM)为速度符号函数；n为迟滞宽度；δ0为速度反转时的电机轴转角。

图5 非线性弹性变形的滞后模型

2 数学模型实验验证

本节通过phET模拟实验软件搭建如图6所示模拟实验平台，对所建立的数学模型进行验证。其通过角度反馈以典型的半封闭控制系统进行控制，分辨率为8 000脉冲/转的电机编码器安装在电机延长轴上，分辨率为2 880 000脉冲/转的负载端编码器通过弹性联轴器与负载连接，测量并评估负载转动角度，并输出角位移。

1-反馈信号输出端口；2-弹性联轴器；3-负载端编码器；4-检测信号输出端口；5-惯性载荷轮；6-电机；7-电机编码器；8-控制信号输入端口图6 模拟实验平台

模拟样机的传动比为50，FS的齿数zf=80，CS的齿数zc=82，且电机轴上电机和负载间的惯性比为1∶3[15]。

2.1 同步分量的模拟实验验证

通过模拟实验得到同步分量的实验波形(实线)和MATLAB建模分析预测波形(虚线)比较如图7所示，其中负载角(横轴)循环往复了3次。由图7可知，该模型可以精确预测传动误差的同步分量。

图7 实验和模型中同步分量的波形比较

2.2 非线性分量的模拟实验验证

将MATLAB分析得到的响应波形与模拟实验得到的波形进行反复比较，然后对数学模型的自由参数进行优化，最后确定的自由参数如表2所示。最终模拟实验所得波形(实线)和MATLAB建模分析预测波形(虚线)中角度传动误差和滞后特性的比较波形如图8和图9所示。

表2 自由参数值

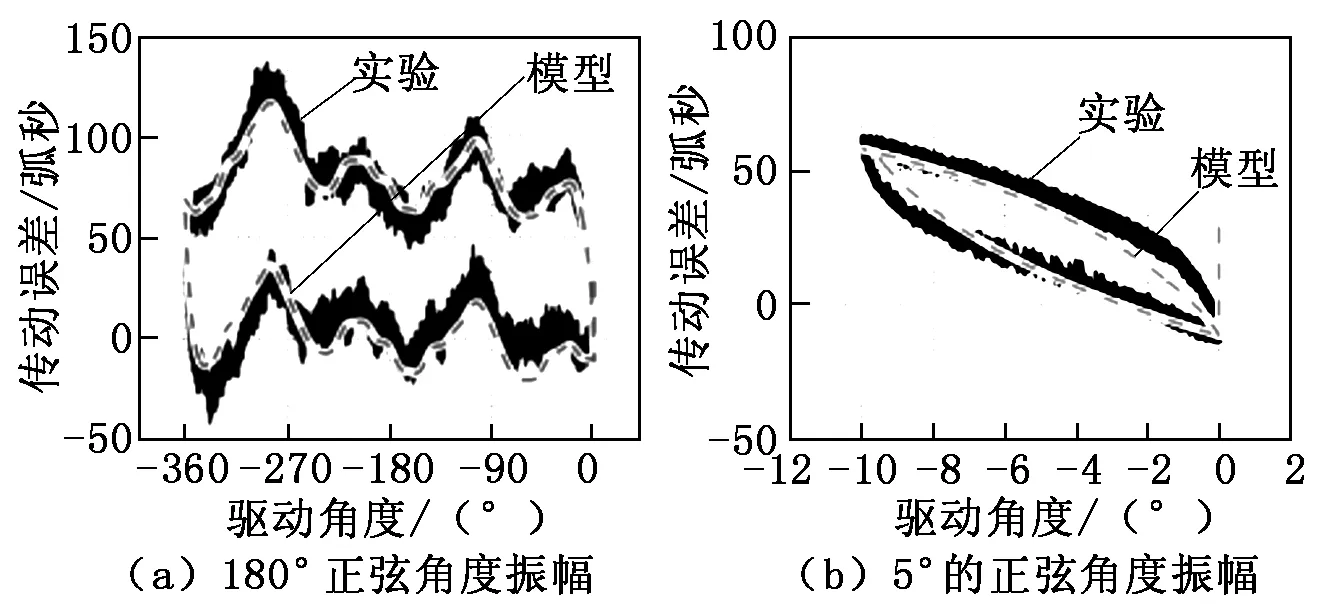
图8 传动误差随驱动角度的变化曲线

图9 传动误差随时间的变化曲线

由图8和图9分析可得，非线性分量模型可以精确地预测角传动误差，验证了所提出数学模型的正确性。

3 角传动误差补偿方法建立及模拟试验

本节主要是以上节新建的传动误差预测数学模型为基础编制控制程序，并将其整合到定位控制系统中，对传动误差引起的稳态角误差进行精确的前置补偿，控制系统中角传动误差的补偿方案如图10所示。补偿角输入值为：

Nθ*TE=N(θSync+θHys).

(7)

其中：N为齿轮系数；θ*TE中的上标*表示反馈量，其基本含义与θTE相同，只是与输出量进行区分。

如图10所示，补偿后系统的最终输入值是从原始电机原始角位移输入值θ*M中减去Nθ*TE得到的。在模拟实验验证中，在顺时针和逆时针方向分别做了间隔周期为2 s的240步微步运动，其中为确保每次微步运动都能为同步分量提供不同角传动振幅的传动误差曲线，所以步进电机的点动步进幅度设为43.56°。

图10 角传动误差的补偿方案

设定目标角度为0弧秒且叠加了240次微步运动，在模拟实验平台上进行顺时针方向的模拟实验，并随后利用MATLAB中的Simulink模块进行编程和图像处理，得到其电机端和负载端角度响应稳定性波形，如图11和图12所示。由图11(a)和图12(a)的响应曲线可推得：传动误差仅会激起负载端的稳态误差，而对电机输入端无明显影响，在负载端角度稳定的过程中及电机和负载端角度出现瞬时的过冲或欠冲时，因角度传动误差会随第1节中分析的角度而变化，故会出现散射响应。图11(a)、图12(a)没有进行任何补偿，稳态角附近角度散射严重；图12(b)和图12(c)的单分量建模补偿，仅在很低程度上削弱了稳态时的角度散射；如图12(d)所示，与上述图片相比，在双分量补偿的情况下，电机角度精确地定位到了目标角度，且双分量综合补偿模型极大降低了稳态时的角度散射，从而有效抑制了负载端的稳态误差。同时，逆时针方向的负载角度响应的稳定性波形如图13所示。逆时针方向转动的分析波形与顺时针方向相同，再次验证了数学模型和补偿方法的正确性。

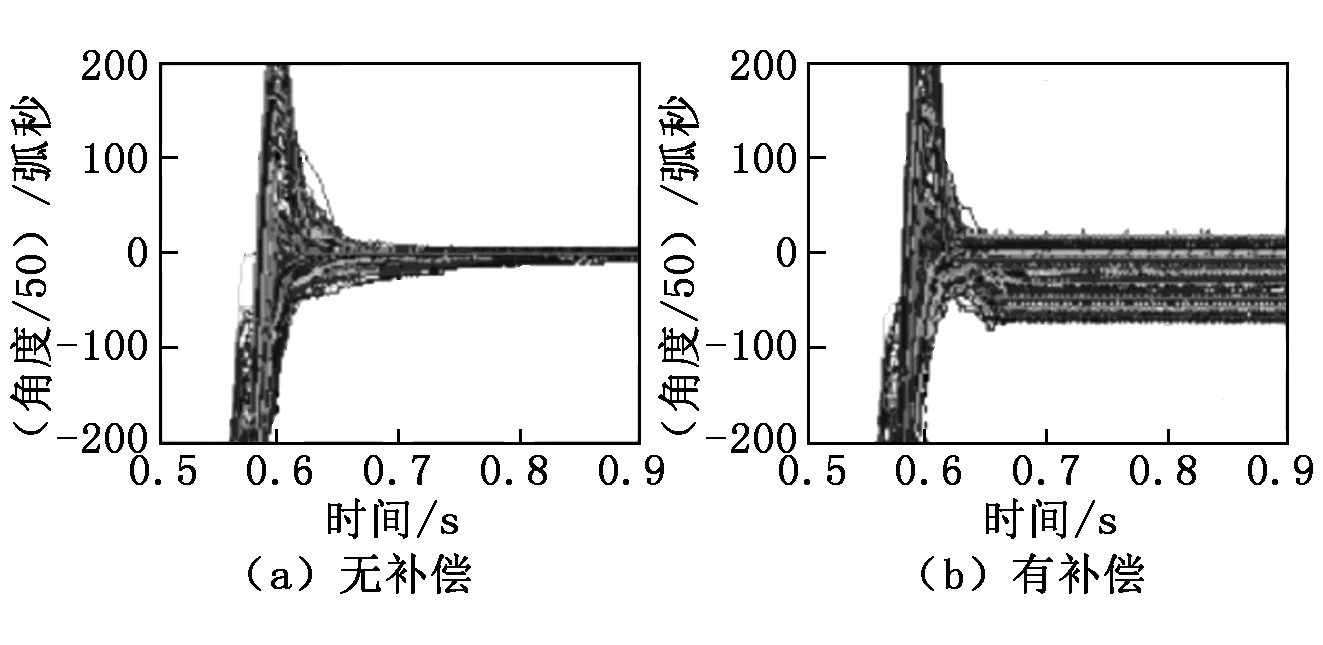
图11 顺时针转动稳定时电机端角度的放大响应波形

为了定量验证模型的补偿性能，每次试验都通过Origin作图评估分析了负载端角度稳态误差的统计值3Δ(正态分布中的3Δ原则)和平均值，如表3所示。表3中每个项目中的第一行表示绝对值，第二行表示由没有补偿的值进行归一化处理后的相对值。

由3Δ的统计结果分析可得，将双分量补偿数学模型应用到新补偿方法中，可以成功将稳态时的角度散射降低40%，大大抑制了负载端的稳态误差，增加了谐波齿轮传动系统的角传动精度和静态定位精度。

图13 逆时针转动稳定时负载端角度的响应波形

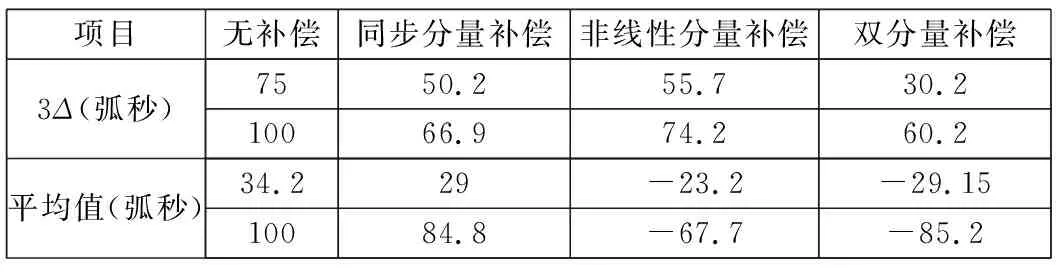
表3 负载端角稳态误差的统计值和平均值

4 结论

本文提出了一种谐波传动齿轮角传动误差及静态定位误差的数学模型及补偿方法，其对静态定位精度在稳定时的性能提升尤为明显。在建模过程中，根据角传动误差在微位移区域表现为周期性脉动和具有滞后特性的非线性特性，将角传动误差分为同步和非线性弹性两个分量。因此，通过对旋转角度的频谱分析方法，完成了同步分量的数学建模；基于具有滞后特性的滚动摩擦建模框架的新数学公式被应用于非线性弹性部件理论，完成了非线性弹性分量的数学建模。将提出的传输误差模型作为基于模型的前馈补偿，应用于谐波齿轮传动的半闭环式控制系统的定位系统中，并进行了模拟试验验证。

一方面，使用仿真软件模拟实验室定位装置进行了数值模拟和模拟实验，验证了所提出的数学模型和补偿方法的正确性。另一方面，通过微步运动进行了模拟定位试验，以建立的误差数学模型为基础，以创新的误差补偿方法为手段，成功补偿了角传动的稳态误差。3Δ定量统计表明，稳态时的角度散射降低了40%，大大抑制了负载端的稳态误差，提高了静态定位精度，最终证明了数学模型和补偿方法的正确性。