螺旋槽专用数控铣床立柱拓扑优化设计
薛柏惠,杨赫然,孙兴伟,董祉序,刘 寅
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
0 引言
螺旋槽专用数控铣床[1]机械结构主要由主传动系统、进给系统及基础支承件等组成,立柱是连接机床床身与刀具的重要基础支承件之一。机床加工过程中,在外载荷作用下立柱的变形和振动会影响机床的加工精度[2]。基于拓扑优化[3]的方法来改善机床的动态特性,可实现整机轻量化设计、降低制造成本。
本文以某系列螺旋槽专用数控铣床的立柱结构为研究对象,在对立柱结构进行静、动态特性分析的基础之上,采用拓扑优化的方法对立柱进行结构优化设计,根据拓扑优化结果改进结构,并利用响应面法对立柱改进结构参数尺寸进行优化选择,在保证制造工艺的前提下,最终确定立柱结构最佳结构廓形及尺寸。
1 立柱有限元分析
1.1 螺旋槽专用数控铣床立柱有限元模型建立
根据某螺旋槽专用数控铣床的整体参数,在三维建模软件SolidWorks中建立该螺旋槽专用数控铣床模型,如图1所示。
机床立柱材料为HT150,简化后的立柱三维模型如图2(a)所示。利用有限元分析软件ANSYS Workbench对其进行网格划分,网格划分后得到单元数为1 568 897个、节点数为1 064 893个,网格平均质量为0.89,网格质量满足分析需求。立柱有限元模型如图2(b)所示。
1.2 立柱静态特性分析
机床切削力载荷常用的计算方法有两种,即指数公式法和功率估算法,本文采用功率估算法对该铣床铣削时产生的铣削力进行计算。功率估算法将切削时电机消耗分为主切削力和进给力所消耗的功率。机床切削力计算相关参数如表1所示。

图1 某螺旋槽专用数控铣床三维模型

图2 立柱三维模型和有限元模型

表1 机床切削力计算相关参数
该铣床在加工时进给力相对于切削力来说很小,忽略进给力所消耗的功率,将切削力功率看成电机功率的主要成分。该铣床工作时立柱所受到的切削力由式(1)及式(2)计算得出[4]:
Fc=Pcvc.
(1)
vc=πdn01 000.
(2)
其中:Fc为机床切削力,N;Pc为切削功率,W;vc为切削速度,m/s;d为刀具直径,mm;n0为刀具转速,r/s。
作用在立柱上的切削力各向分力可由式(3)计算得出:
Fx=F2c-F2z-F2yFy=0.3FcFz=0.5Fc.
(3)
其中:Fx为X向切削力,N;Fy为Y向切削力,N;Fz为Z向切削力,N。
在有限元分析软件ANSYS Workbench的静力分析模块中施加由式(3)计算得出的切削力,同时对立柱有限元模型施加约束及载荷。最终获得的立柱总变形云图、等效应变云图和等效应力云图分别如图3~图5所示。
通过静力分析可知,机床立柱最大变形出现在立柱前侧与顶部连接处,最大变形量为20.48 μm,由立柱应力和应变云图得出立柱在X轴负方向发生弯曲。
1.3 立柱模态分析
立柱的动态特性反眏其受外部激振时的结构稳定性。其中低阶模态基本决定了立柱的动态性能,通过模态分析得到的立柱前4阶振型云图如图6~图9所示。

图3 立柱总变形云图 图4 立柱等效应变云图 图5 立柱等效应力云图

图6 立柱第1阶振型云图 图7 立柱第2阶振型云图 图8 立柱第3阶振型云图

图9 立柱第4阶振型云图
根据模态分析结果可知,立柱1阶固有频率下的模态振型为立柱上部沿Y轴左右摆动,2阶固有频率下的模态振型为立柱上部沿X轴前后呼吸振动。
2 立柱拓扑优化
由上述分析结果可知,立柱虽然满足使用设计要求,但立柱前侧与顶部连接处为变形量最大的位置,立柱前侧右地脚等效应力偏大。在不影响装配的情况下,为保证加工精度,可对立柱前侧进行结构优化,改善立柱的动静态特性;并通过拓扑优化的方法,获得立柱材料质量的最佳分布。
本文采用拓扑优化方法中的变密度法对立柱结构进行优化设计,在拓扑优化的数学模型前引入特征函数:
ρ(x)=0x∈θvoid1x∈θmat.
(4)
其中:ρ(x)为结构材料的特征属性;θvoid为孔洞区域;θmat为实体结构区域。若某处为保留区域,特征属性赋值为“1”;若此处为可移除区域,则材料被删除,特征属性赋值为“0”。本文中立柱的拓扑优化数学模型表示为:
findX=[x1,x2,…,xn]T
mininizef(X)=FTUs.t.V≤V*F=KUxi∈{0,1}i=1,2,3,…,n.
(5)
其中:xi为特征变量,即设计变量;n为设计变量的个数;f(X)为目标函数,代表立柱结构的柔度;F为结构所受外力向量;U为结构位移向量;V为优化后立柱体积上限值;V*为优化前体积;K为总刚度矩阵。
在拓扑优化求解设置中,考虑到立柱装配布置的需求,为避免优化后立柱结构改变使其与其他结构件装配发生干涉,排除立柱前侧、地脚固定区域、立柱顶部及立柱后侧,其余部分为优化区域。
使用ANSYS Workbench的拓扑优化模块对立柱进行拓扑优化计算。最终立柱正面和底面的优化结果如图10所示。

图10 立柱优化结果
在优化分析结果中,将保留结果值定义为0.1,可移除区域显示为立柱前侧偏上部分区域、立柱底部中间区域和立柱后侧丝杠装配区域。为提高立柱刚度,在立柱前侧中间部分增加筋结构。
3 基于响应面法的立柱结构尺寸优化
采用响应面优化法对立柱改进尺寸进行优化设计,设定多目标优化对立柱尺寸进行最优选取。
对拓扑优化后的立柱尺寸进行优化,其中11个设计变量相对独立互不干涉,同时考虑到立柱装配和制造工艺要求,对11个设计变量制定取值范围,立柱优化选取参数名称、初始值及取值范围如表2所示。
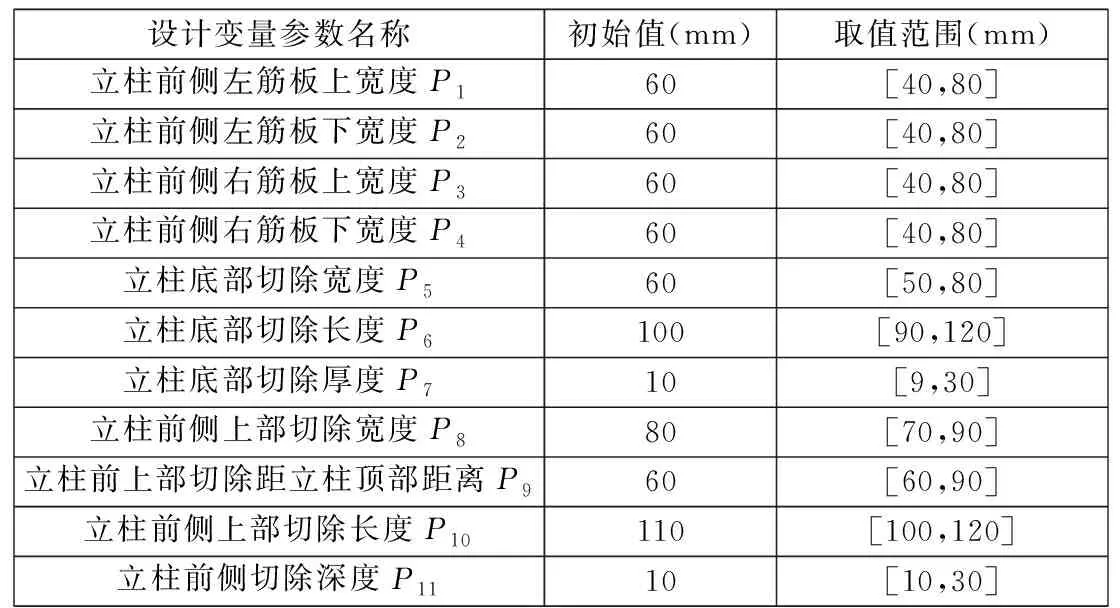
表2 立柱优化选取参数名称、初始值及取值范围
考虑到试验设计的经济性以及结构优化分析的高效率和适用性,采用拟合精度较高的Box-Behnken Design(BBD)方法[5]计算出每组的最大变形量、等效应变值、等效应力值和前4阶固有频率值。设置立柱多目标函数和约束条件如下:
minimizeDminimizeσminimizeδminimizemmaximizeM1maximizeM2maximizeM3maximizeM4s.t.m≤m*,σ<[σ].
(6)
其中:D为立柱最大变形量;σ为立柱等效应力最大值;[σ]为材料许用应力;δ为立柱最大等效应变;M1~M4分别为立柱第1阶~第4阶固有频率值;m*为立柱原始总质量;m为立柱优化后总质量。
4 立柱优化结果分析
在ANSYS Workbench软件中,使用基于响应面法优化[6]模块对设计变量进行多目标寻优,对最终结果圆整后的立柱设计变量最优结果如表3所示。

表3 立柱设计变量最优解
对优化后的结构进行仿真分析,并对立柱优化前、后的性能参数进行对比,结果如表4所示。由表4可知:最大变形量减小了24.9%,最大等效应力减小了21.3%,最大等效应变降低了15.9%,1阶~4阶固有频率都有一定程度的提升,立柱优化后质量减轻且改进后立柱的铸造难度没有增加。

表4 立柱优化前后性能参数对比
5 结语
为改善螺旋槽专用数控铣床立柱的工作性能,从而保证机床的加工高精度,在对立柱进行有限元分析的基础上,运用拓扑优化方法对其结构廓形进行改进并基于响应面优化的方法确定立柱结构的最优尺寸。优化后的立柱在质量有所降低的情况下,其最大变形量、最大等效应变、最大等效应力均有所下降,且其前几阶固有频率均有较显著的提升。本文提出的方法为机床类产品的关键零部件或类似机械结构优化设计提供了理论指导。

