永磁同步电机模糊滑模速度控制器设计

禹聪， 康尔良

(1.哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150080；2.黑龙江省高校直驱系统工程技术创新中心，黑龙江 哈尔滨 150080)

0 引 言

近几年，永磁同步电机(permanent magnet synchronous motor，PMSM)由于其存在效率高、功率密度以及体积较小等几大优势被广泛地应用到很多领域，同时国内外学者针对PMSM的控制策略以及控制方法做了大量的研究和实践[1-2]。传统的PMSM控制方式PI控制存在着鲁棒性差、系统不稳定等问题，不能满足控制系统的高性能要求[3]。

为了满足系统的控制要求、提高PMSM的控制性能，学者及研究人员针对PMSM的控制方法进行了研究，针对其控制方式主要可以分为几种类型， 如矢量控制[4]和直接转矩控制[5]等，同时针对控制系统提出了很多现代控制方式，例如滑模控制[6-8]、自适应控制[9-10]、模型预测控制[11-12]、神经网络控制[13]等方式。

滑模控制(sliding mode control,SMC)由于其具有强鲁棒性以及对系统不确定性不敏感等优势被广泛应用于运动控制、过程控制等领域[14]。SMC与传统PI控制的区别在于其控制的不连续性，它的运动过程可以分为两段运动，其一是系统状态量在状态空间规则下趋向滑模面的运动，其二是状态变量受到在滑模面两侧空间规则以及滑模面规则下做穿插滑动的运动，通过设计趋近律函数保证了系统状态变量能在有限的时间内到达收敛点，从而使得系统在有限时间内收敛。

但是传统的SMC存在着超调量大、响应速度慢以及抖振等问题，抖振是SMC固有的一个问题，其根源在于控制函数的不断切换，它会导致系统转速波动和系统不稳定，抖振的削弱也一直是研究的热门话题[15]。文献[16]设计了一种新型的模糊自抗扰控制器，将模糊逻辑引入自抗扰控制器中改善了系统的动态响应性能，论文研究了低转速的情况，且转速波动较大。文献[17]提出了一种新型的滑模速度控制器，其采用了一种用于侧线模式的高稳定滑模面，由仿真得知此新型滑模控制器相比于传统的SMC系统具有更快的动态响应、更高的稳定性。文献[18]设计了一种新型的模糊控制方式，通过采用模糊控制理论使得滑模增益自整定，相比于传统的SMC控制系统而言，此系统动态性能更好，同时具有较强的抗干扰能力。

本文针对传统SMC系统中存在的超调量大、动态响应慢以及抖振问题采用基于模糊控制的滑模控制方式设计一种模糊滑模速度控制器(fuzzy sliding mode speed controller,FIMSMC)。系统采用指数趋近作为系统状态量的趋近方式，引入模糊控制理论，采用模糊控制方式对滑模增益进行动态调节，FIMSMC相对于传统SMC控制提高系统的动态响应速度、抗干扰能力以及有效削弱系统的抖振问题。

1 滑模控制理论

一般情况下的非线性系统

(1)

式中：x∈Rn,y∈Rm为系统的状态量和控制器变量。

其滑模面函数为

s(x,t),s∈Rm。

(2)

控制器函数如下：

(3)

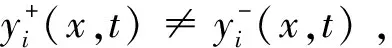
1)滑动模态存在；

3)滑模运动的稳定性。

以上3点是滑模控制的基本条件，系统可以在有限时间达到稳定状态。

本文采用指数趋近律作为控制器的滑模控制律为

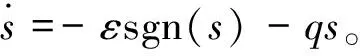
(4)

定义滑模面函数为

(5)

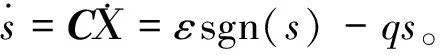
(6)

y=(CB)-1[-CAΧ-εsgn(s)-qs]。

(7)

2 模糊滑模速度控制器

2.1 改进滑模速度控制器设计

为了方便滑模控制器的设计，基于d-q坐标轴下建立表贴式PMSM的数学模型如下：

(8)

式中：Ls为定子电感；R为电阻；在d-q坐标系下ud、uq为电压；id、iq为电流；pn为电机极对数；wm为机械角速度；ψf为永磁磁链；TL为负载转矩；J为转动惯量。

系统采用id=0转子磁场定向的控制方式，此方式能够有更好的控制效果，此时式(1)可表示为：

(9)

定义PMSM控制系统的状态变量为：

(10)

式中：x1、x2为系统状态变量；wr为定义转子转速；wm为电机实际转子转速。

由式(2)、式(3)可得：

(11)

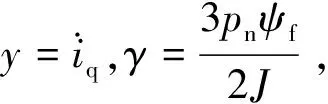
(12)

定义此滑模控制的函数为

s=cx1+x2。

(13)

式中c>0为滑模设计参数，由式(13)求导可得

(14)

由式(4)、式(14)可得

(15)

(16)

采用指数趋近律作为系统状态变量的趋近方式，针对其切换函数，本文采用平滑切换的sigmoid(s)函数代替不连续的sgn(s)符号函数

(17)

Sigmoid函数如图1所示。

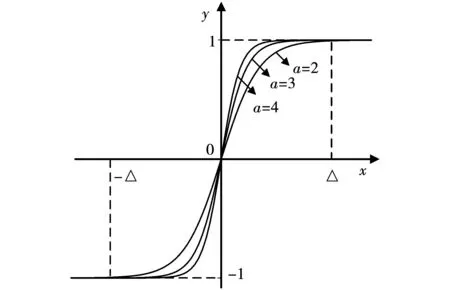
图1 Sigmoid函数图像Fig.1 Sigmoid function image

由图1可知，随着a的增大，sigmoid(s)切换函数过零点部分函数曲线越陡，抖振削弱效果越差，本文采用a=2时的平滑切换sigmoid(s)函数作为滑模控制的开关函数

(18)

2.2 模糊控制器设计

为了提高系统的动态响应性能以及减小滑模本身固有的抖振问题，本章研究了模糊逻辑理论，将模糊控制引入SMC中，采用动态滑模增益的形式对系统进行更为精准的控制，将系统状态量趋近滑模面的距离动态关联滑模增益设置模糊规则，实现系统滑模趋近速度以关联的模糊规则动态变化，通过模糊关联规则输出实现系统状态量的趋近速度动态变化。

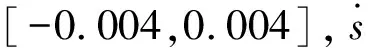
设计模糊规则如表1所示。

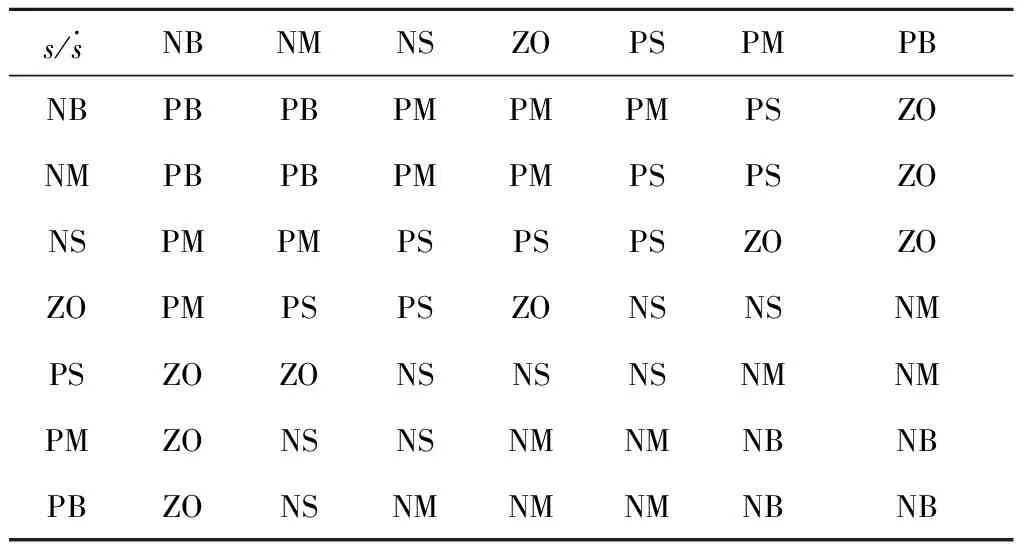
表1 控制规则

如表1所示，模糊控制设计为7个模糊子集，同时设计为7个模糊输出，系统采用Mamdani模糊算法和重心反模糊化。输入输出量采用三角形隶属度函数如图2～图4所示。

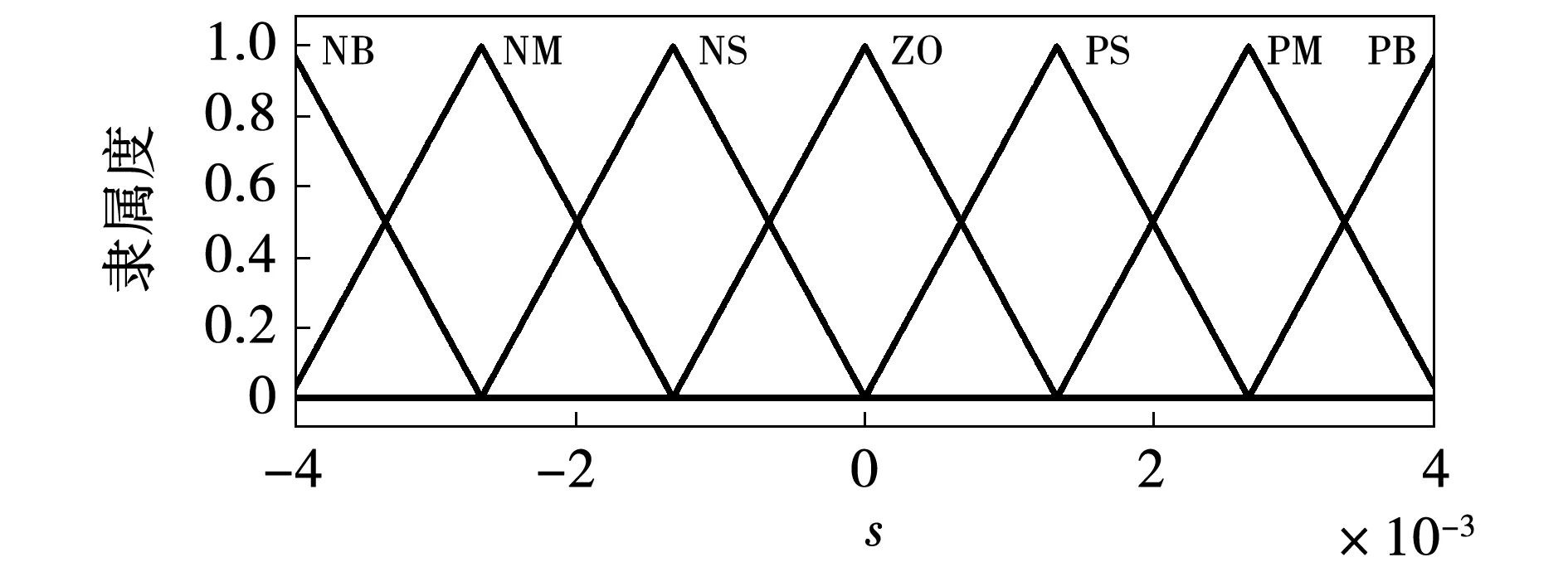
图2 输入s的隶属函数Fig.2 Enter the membership function of s

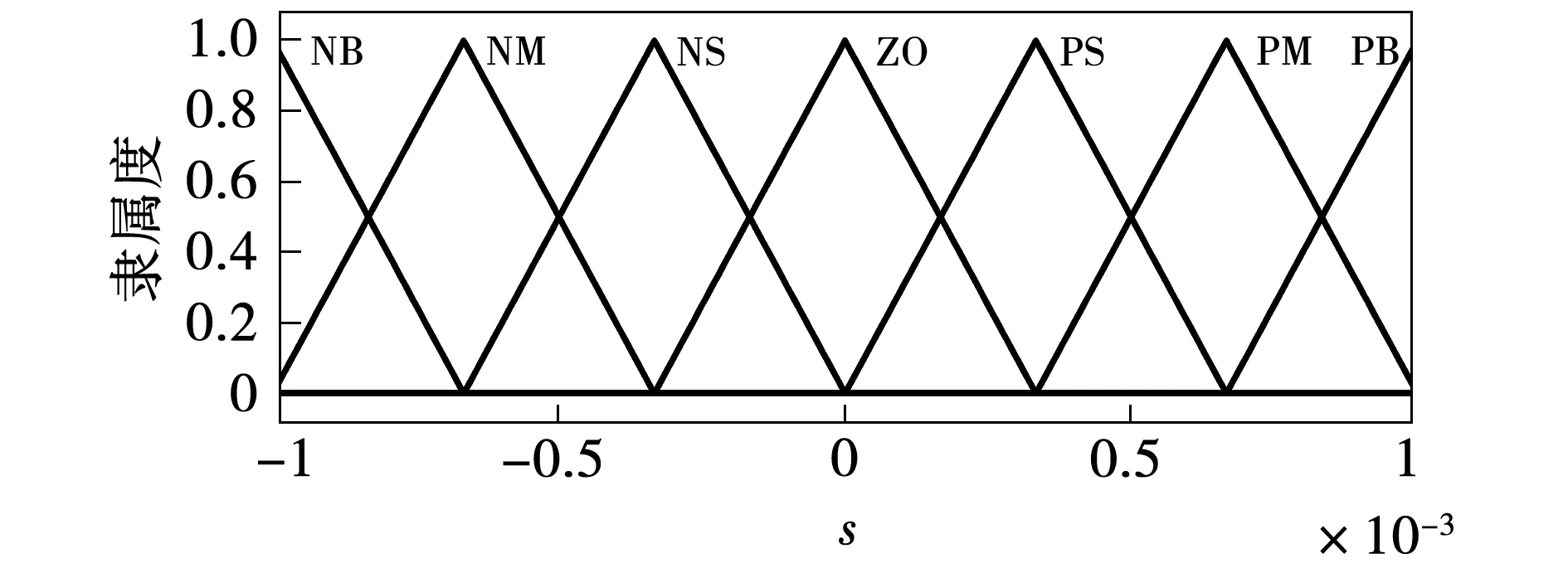
图3 输入的隶属函数Fig.3 Enter the membership function of

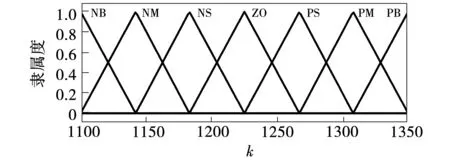
图4 输出P(s)的隶属函数Fig.4 Membership function of output P(s)

将控制规则引入改进滑模控制器(improved sliding mode controller,IMSMC)中，实现了滑模增益的自整定，系统状态变量距离滑模面较远时会通过模糊关联规则输出大增益值，状态变量距离滑模面较近时会通过模糊关联规则输出小增益值，此方式可以提高系统的动态响应速度，实现系统无超调启动，同时有效地削弱系统的抖振，使得系统转子转速波动减小。

3 仿真和实验验证

为了验证本文提出方案，本节通过Simulink进行模型搭建，系统采用id=0控制方式，设定仿真时间为0.2 s，搭建实验平台以此方式验证了本文所提控制策略。永磁同步电机参数如表2所示。

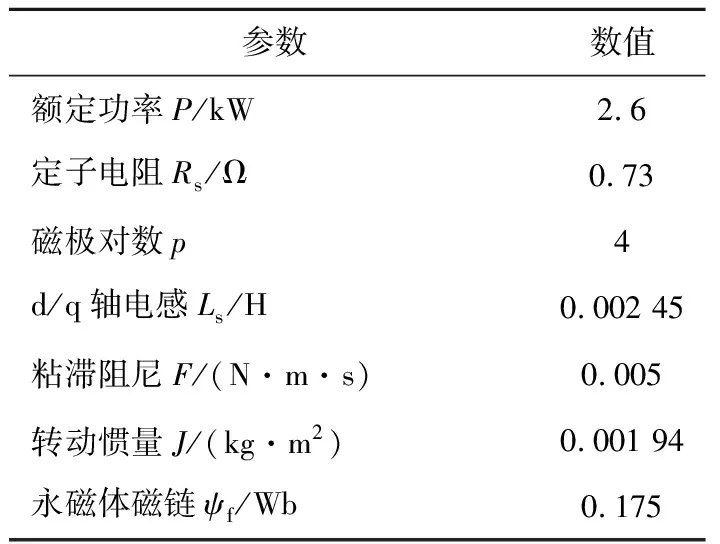
表2 PMSM参数

永磁同步电机控制系统框图如图5所示。

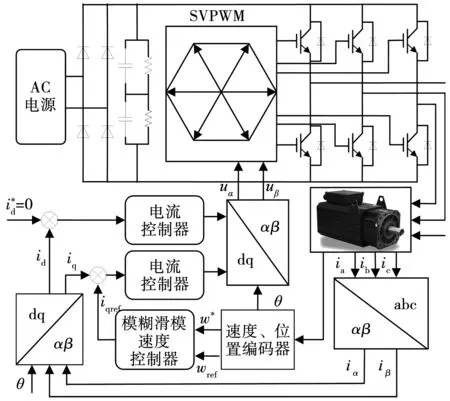
图5 永磁同步电机系统框图Fig.5 System block diagram of permanent magnet synchronous motor

传统SMC与IMSMC系统仿真波形如图6、图7所示。

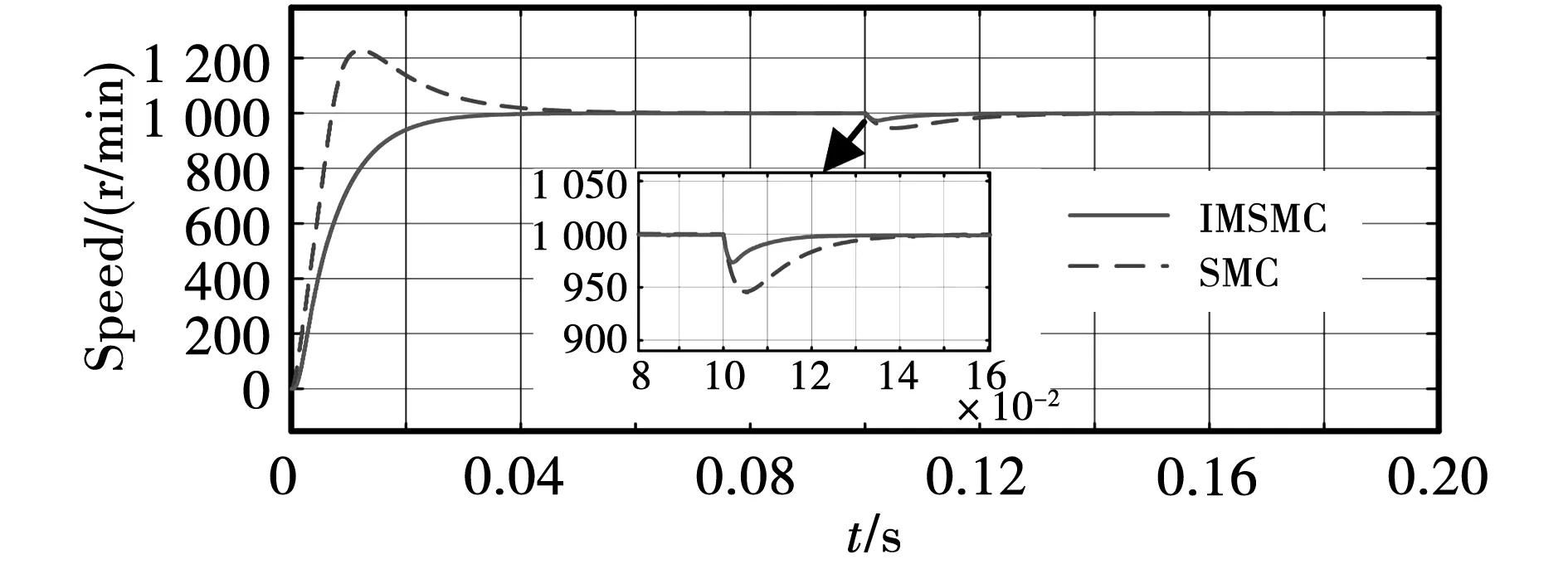
图6 传统SMC与IMSMC控制系统速度波形Fig.6 Speed waveform of traditional SMC and IMSMC control system

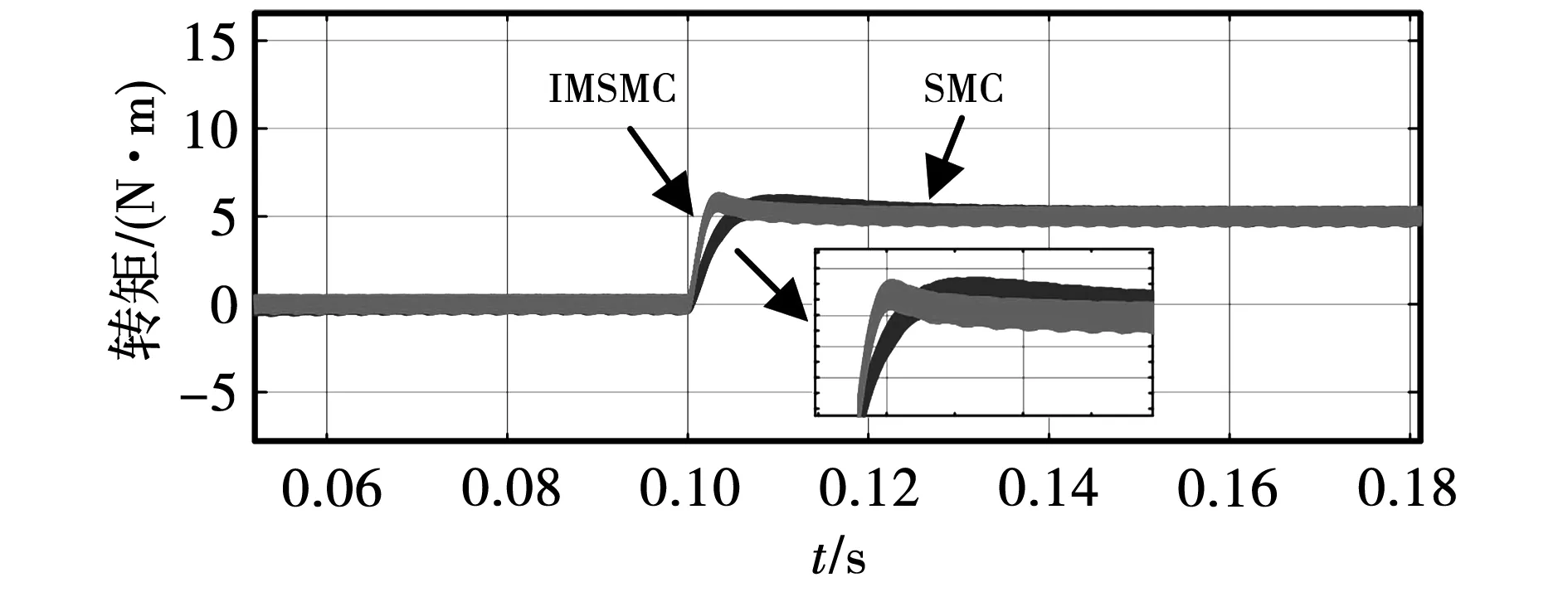
图7 突加负载时IMSMC与SMC控制系统转矩波形Fig.7 Torque waveforms of IMSMC and SMC control systems when a sudden load is applied

由图6可知，传统SMC控制器作为系统速度环控制时其转速存在较大的超调量，且抗干扰能力较弱。IMSMC相较于传统SMC鲁棒性更强，可以实现无转速超调启动。

在0.1 s时突加5 N的负载，如图7所示，IMSMC系统可以更快恢复稳定，相较于传统SMC控制，其响应速度更快，提高了系统稳定性。

IMSMC与FIMSMC系统仿真波形如图8、图9所示。

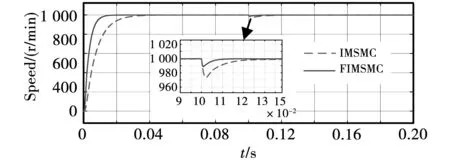
图8 FIMSMC与IMSMC控制系统速度波形Fig.8 Speed waveform of FIMSMC and IMSMC control system

由图8、图9可知，FIMSMC相较于IMSMC动态响应能力更强，具有更快的响应速度。在0.1 s时系统突加5 N的负载，FIMSMC相比于IMSMC的鲁棒性更强，有效提高了系统的动态响应性能,能够更快地使系统达到稳定。

图9 突加负载时FIMSMC与IMSMC控制系统转矩波形Fig.9 Torque waveforms of FIMSMC and IMSMC control systems when a sudden load is applied

FIMSMC与SMC控制试验平台以及波形图如图10～图16所示。

图10 试验平台Fig.10 Test platform

由图11、图12所示，参考转速设定为1 000 r/min时，SMC控制动态响应速度较慢，动态性能较弱。由转速波形可知，SMC控制具有较大的转速超调量，达到稳定所需的时间较长。由转矩波形可知，突加5 N的负载时系统需要更长时间达到稳定。

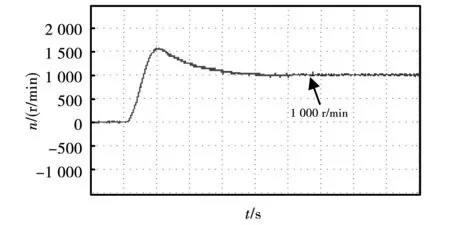
图11 SMC控制速度波形Fig.11 SMC control speed waveform

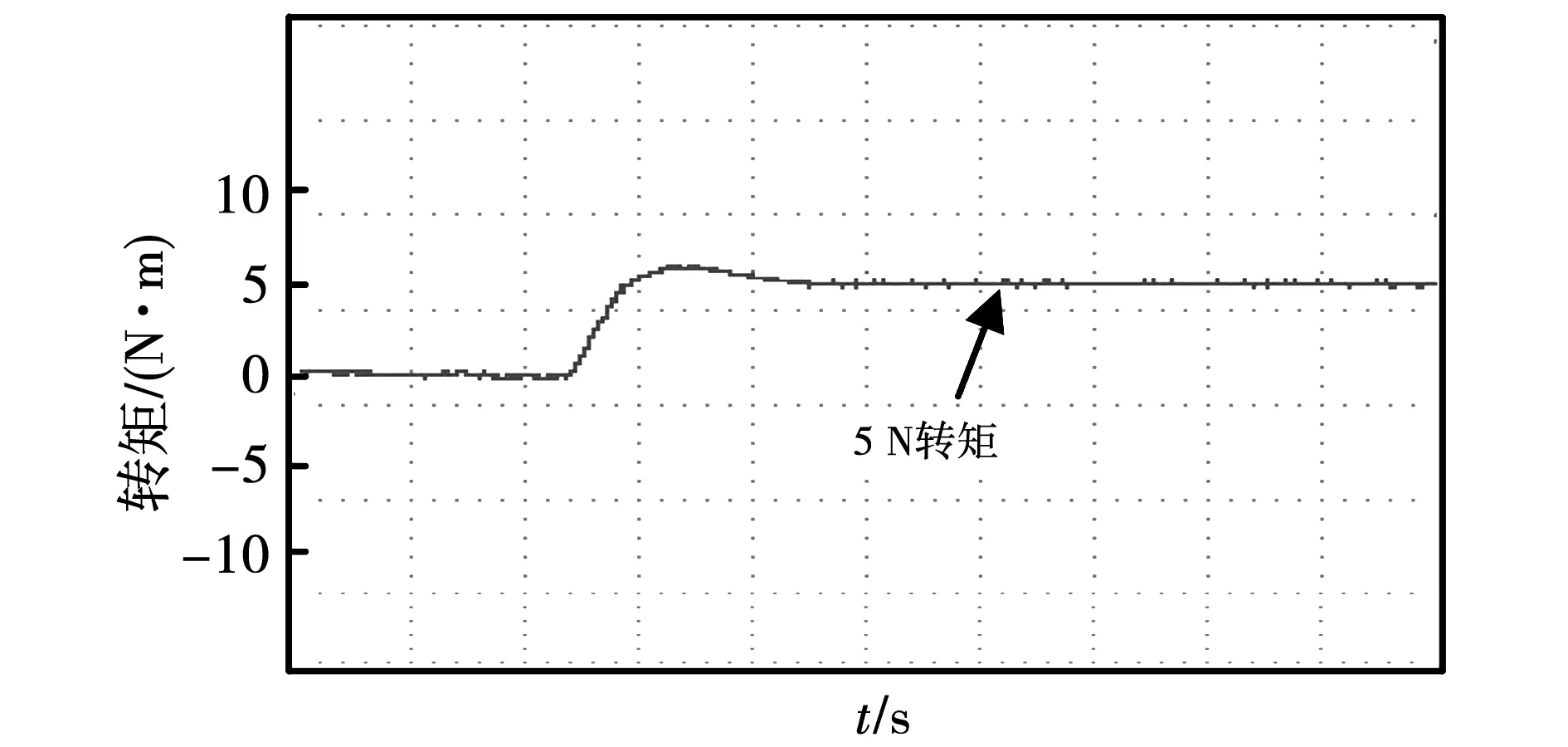
图12 SMC控制转矩波形Fig.12 SMC control torque waveform

如图13所示，给定转速为1 000 r/min,突加和突减负载设置为5 N，由波形可知FIMSMC抗干扰能力较强，突加和突减负载时系统可在较短时间达到稳定。

如图14所示，设置给定转速为600 r/min以及1 000 r/min,由波形可知FIMSMC控制动态响应速度较快，系统能够更快地达到稳定。

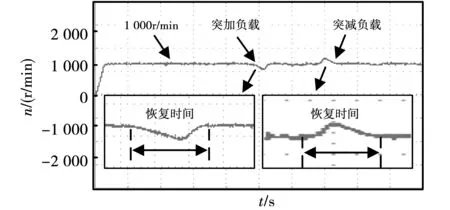
图13 FIMSMC系统突加和突减负载实验波形Fig.13 FIMSMC system sudden load and sudden load reduction experiment waveform

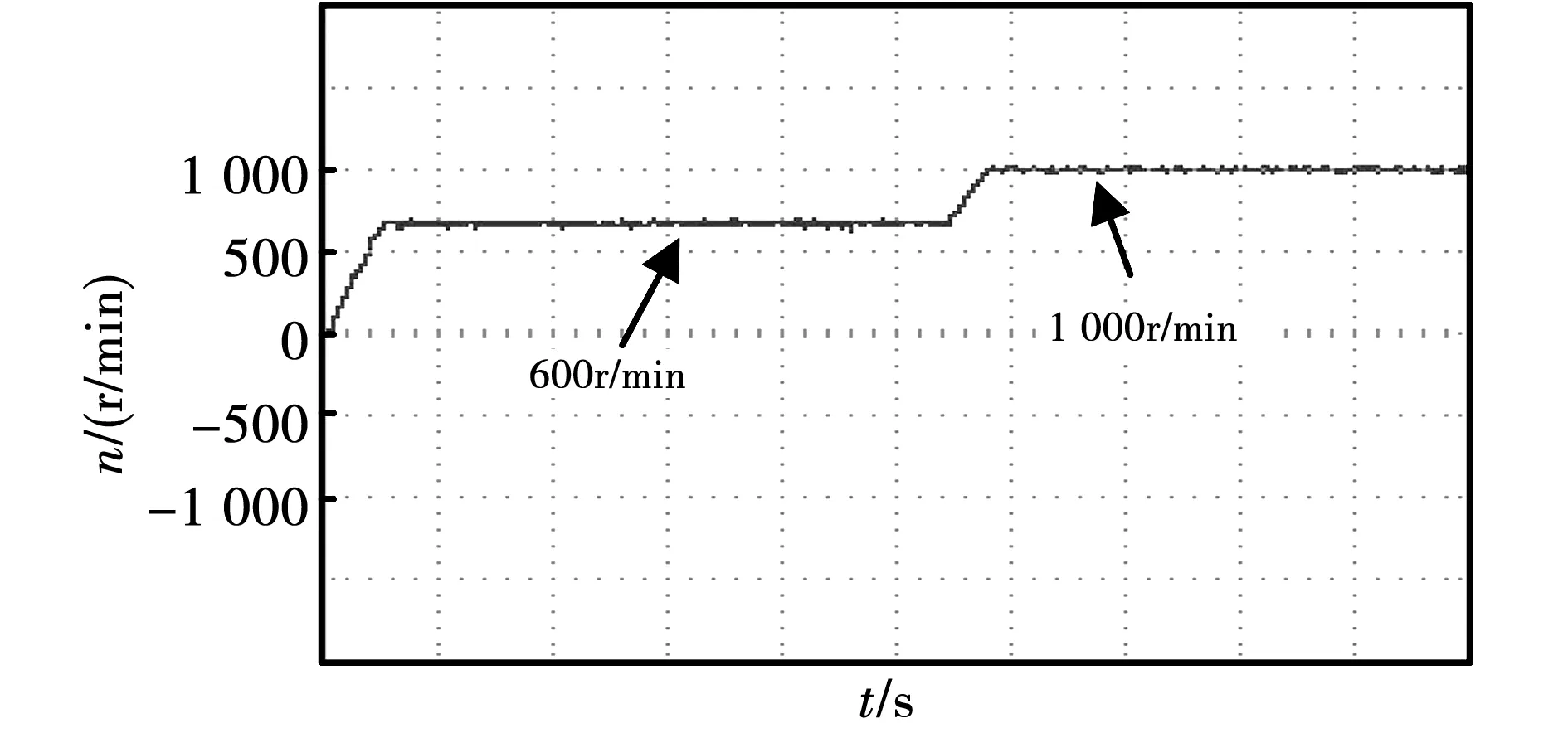
图14 FIMSMC控制变速时转速波形Fig.14 FIMSMC controls the speed waveform during variable speed

如图15、图16所示，设置突加和突减负载为5 N，可知FIMSMC控制动态响应能力强，响应速度快，突加负载时转矩超调量较小，系统能够以更快的速度达到稳定。

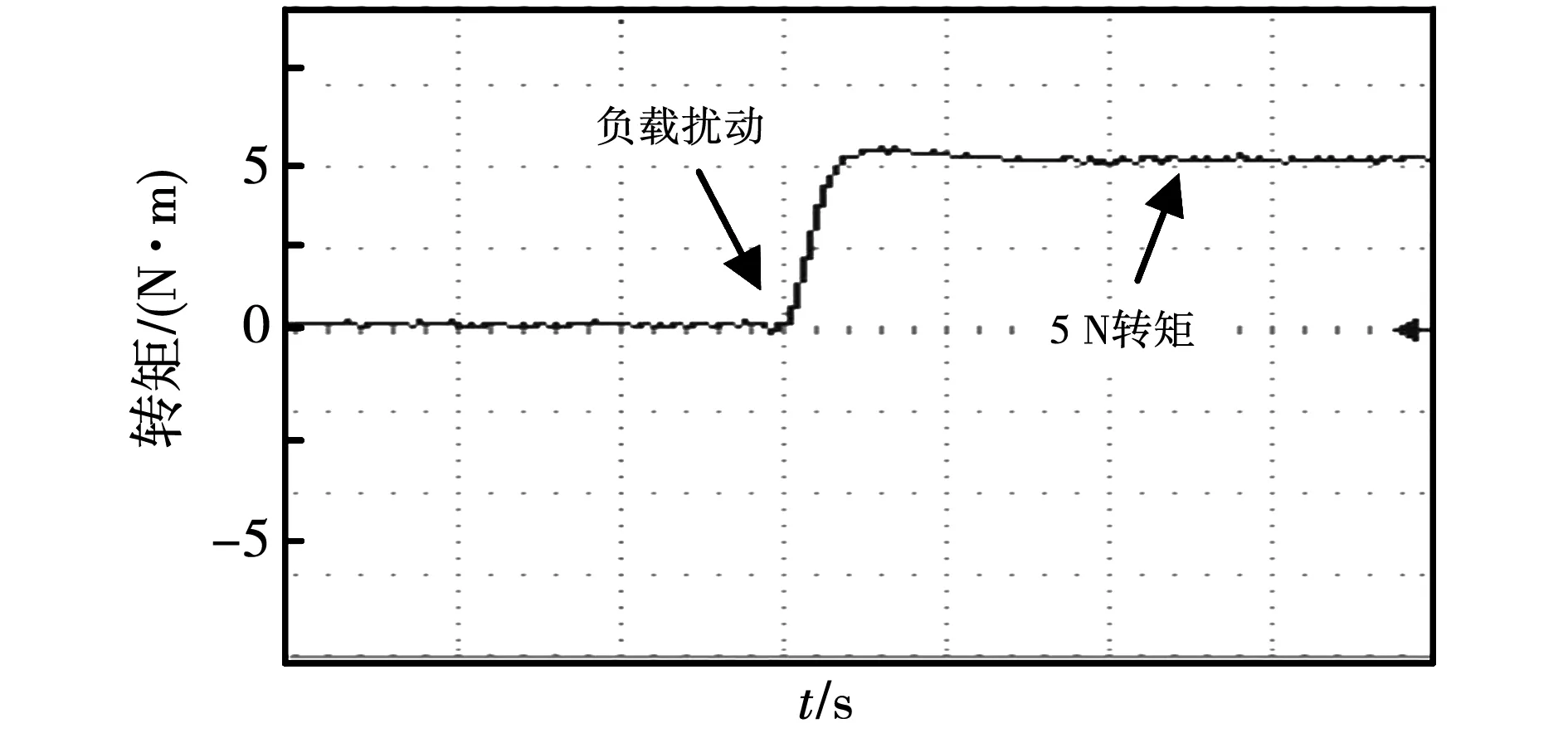
图15 FIMSMC控制系统突加负载时转矩波形Fig.15 Torque waveform of FIMSMC control system when a sudden load is applied

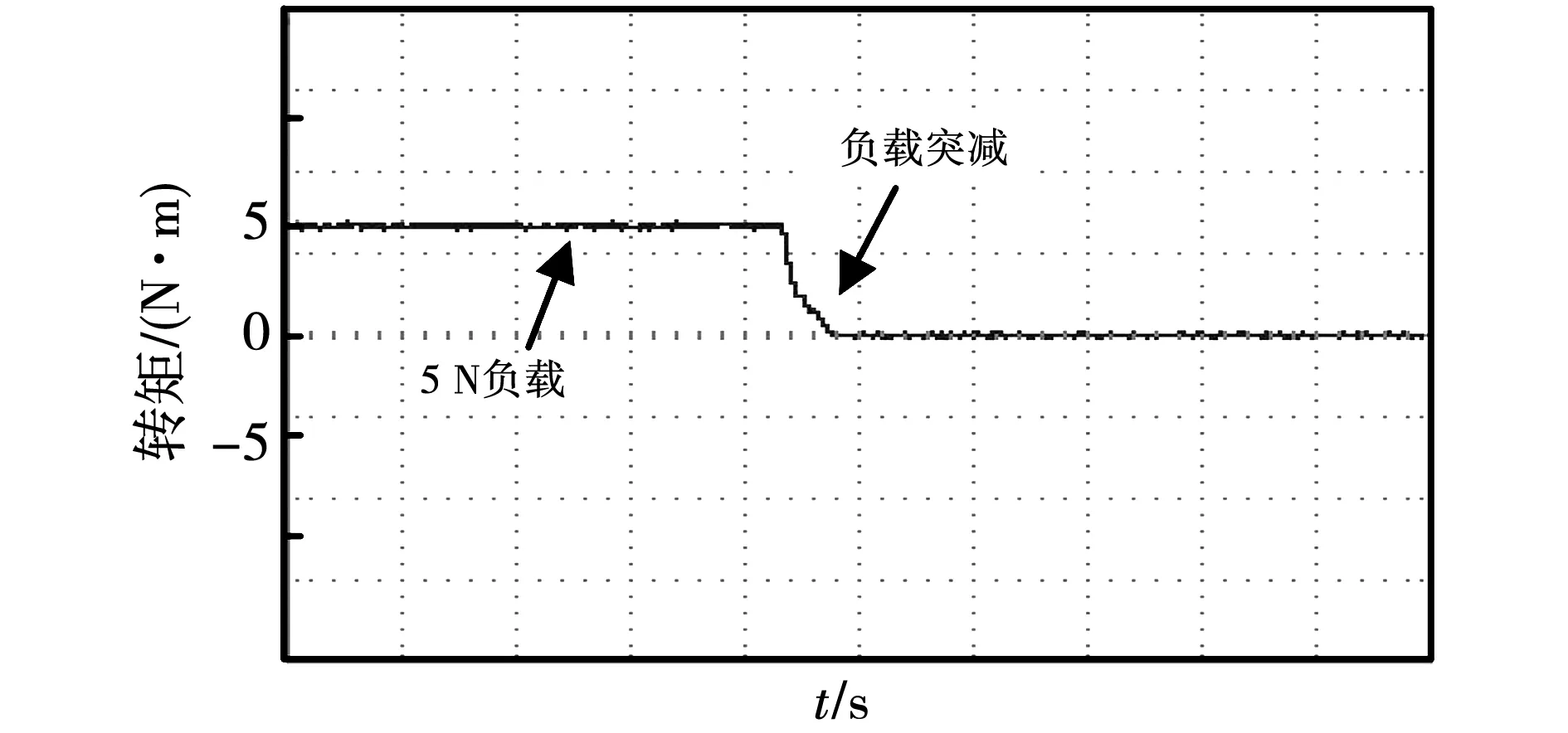
图16 FIMSMC控制系统负载突减时转矩波形Fig.16 Torque waveform of FIMSMC control system when the load suddenly decreases

为了验证本文所提控制策略的有效性，系统采用TMS320F28335控制板作为实验系统的核心板，实验通过负载变动与SMC控制系统进行对比。系统转速设置为1 000 r/min，设置突加突减负载为5 N。

实验可知FIMSMC控制系统动态响应速度更快，提高了系统抗扰动能力以及系统的动态性能和静态性能。实验验证可知FIMSMC相比于SMC具有更快的响应速度，抗扰动能力更强，控制效果更好。

4 结 论

本文针对传统SMC控制器存在的超调量大、动态性能差、抗扰动能力弱以及抖振等问题提出了一种IMSMC，此控制器相对于传统SMC控制器提高了系统的动态响应速度，实现了系统转速无超调启动，在0.1 s突加5 N的负载时系统可以更快地恢复稳定状态，具有较强的抗扰动能力。

在提出的IMSMC基础上，针对其动态性能进行改善并提出了一种FIMSMC。此控制器将模糊控制理论引入IMSMC控制器中控制滑模增益值随着与滑模面的距离的变化而变化，使得切换增益自整定。经过仿真和实验验证FIMSMC相较于SMC动态响应速度更快、系统的动态性能更强以及提高了系统抗扰动能力。