考虑长度修正的半波长输电线路双端故障定位方法

束洪春， 唐玉涛，2， 韩一鸣， 吴玉容， 代月， 蒋晓涵， 薄志谦

(1.昆明理工大学 电力工程学院，云南 昆明 650500；2.昆明理工大学 国土资源工程学院，云南 昆明 650500)

0 引 言

中国“十四五规划”已将“碳达峰”“碳中和”纳入重点任务，全社会碳排放量在2030年前达到峰值，之后逐渐下降，于2060年前达到二氧化碳“零排放”[1]。我国目前正处于工业化和城镇化快速发展的阶段，对绿色能源的需求巨大，目前我国的能源消费还是以高碳消费为主，为了实现“十四五规划”及“2035远景目标”，大量开发使用清洁能源是快速降低碳排放的关键。然而，从我国的能源分布来看，大量风能、光伏资源位于我国西部、西北地区，大量水能资源分布在我国南部及西南地区，将这些清洁能源输送至东部沿海等负荷中心的地理跨度几乎都在2 000 km以上[2-3]，因此，发展超远距离点对点大容量输电具有了更加广泛的意义和实用价值[4-6]。

特高压半波长交流输电(ultra-high voltage half-wavelength AC transmission line,UHV-HWACT)技术是指输电距离接近半个工频(50 Hz)波长，即3 000 km的超远距离交流输电方式。自上世纪40年代被苏联学者提出以来[7]，几十年间有不少学者对其做出过研究。作为一种长距离、大容量的交流输电方式，半波长交流传输技术具有整条输电线路上的无功功率自平衡的优点，不需要安装无功功率的相关补偿设备，根据传输线理论，半波长输电线路等效的电气距离为0，理论上线路的输电能力为无穷大[8]。在经济特性方面，与特高压直流输电技术相比，半波交流输电技术利用了纯交流系统的自然特性，无需额外运行控制设备，且在输送相同功率的情况下输电成本仅为UHVDC的一半[9]。

目前对半波长输电线路的研究多停留在经济性及稳定性方面，对半波长输电线路精确故障定位的研究较少。文献[10]提出了一种基于行波波速特性的半波长输电线路故障测距方案，利用线模波速衰减特性，采用变化的波速实现故障定位；文献[11-12]提出了在线路上布置多测点的故障定位方法，从一定程度上解决了行波的色散问题，但是沿线布置的多测点同步启动及录播数据时刻匹配问题成为新难点。针对半波长输电系统亟需一种精确、快速且原理简单的故障定位方法，结合目前已有方法存在的问题，本文提出基于派克变换的半波长输电线路双端行波测距方法，该方法精确度较高，且不受故障类型、过渡电阻及故障角的影响。在此基础上，本文还考虑超长输电线路长度误差给故障定位带来的准确性问题，通过内部及外部因素分析造成线路长度增大的原因，通过对线路长度进行修正，将最终测距结果归算到各基杆塔编号，进一步提高该方法的工程实用性。

1 派克变换基本原理

2000年，派克变换被北美电力研讨会评选为“20世纪电气工程领域最突出贡献”之一。其基础是“任何一组三相平衡定子电流产生的合成磁场，总可以由两个轴线互相垂直的磁场所代替”的双反应原理[13]。其过程是：将交变的电气量(如电压、电流或磁通量)在静止的α、β轴上的投影等效到旋转的d、q轴上，其中，投影到α、β轴上的过程称为Clarke变换。其作用是：观测点从固定的视角转移到旋转交变的视角上去，在建立如转子回路电磁关系等微分方程时，将随着时间和空间量变化的系数矩阵转化为了常数矩阵，简化了一系列的微分方程的求解。

下面以图1所示坐标系统为例展示派克变换的推导过程。

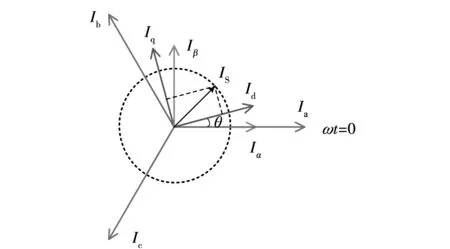
图1 派克变换坐标系统Fig.1 Coordinate system of the Park’ transformation

设三相电流为：

(1)

不难得出：

(2)

由式(1)、式(2)可得：

(3)

即可得出Clarke变换为

(4)

将d、q轴向α、β轴投影可得：

(5)

结合式(1)～式(5)可得，派克变换矩阵为

(6)

为使派克变换可逆，通常引入0轴分量，定义i0为

(7)

可得派克变换为

(8)

其逆变换为

(9)

可将上述变换过程直观地展示如图2所示。

简言之，派克变换是将线模分量Iα和Iβ变换到旋转的坐标上。从物理意义上讲，派克变换就是将三相电压或电流变换到d、q、0坐标轴上，对于对称三相电压或电流，经过派克变换后，成为直流量。

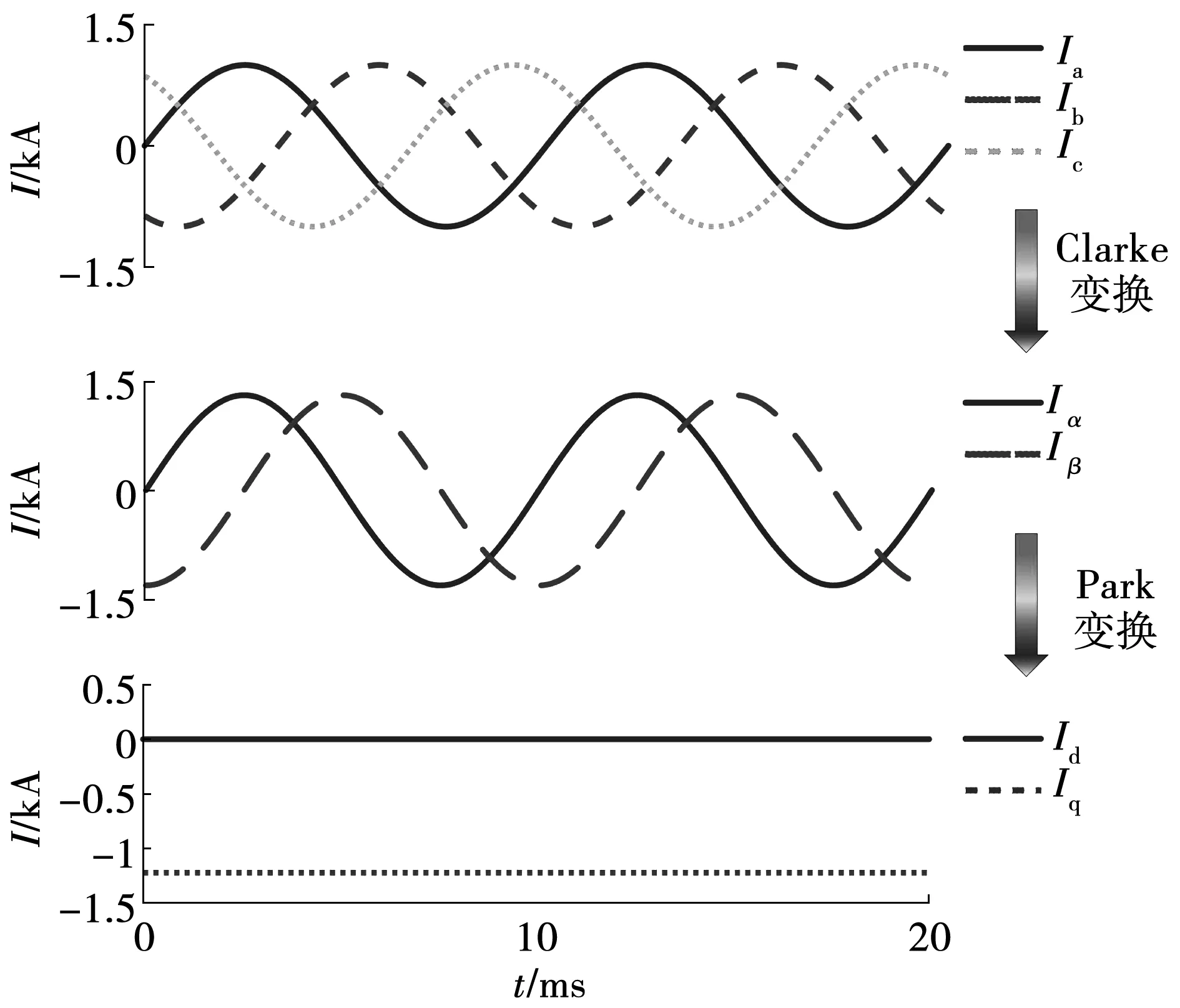
图2 派克变换过程Fig.2 Process of the Park’ transformation

2 基于派克变换的半波长双端测距

特高压半波长线路由于超长的传输距离使得其在继电保护方案设计时需考虑线路参数的频变特性，行波在沿着线路传播的过程中会发生一定的畸变和衰减，行波的初始波头随着传播距离的增加会变得越来越平缓，相较于普通线路而言，行波在超长的交流输电线路上传播将导致更加严重的波形上的衰减和畸变。

行波的衰减可用下式计算[14]：

A=e-γx。

(10)

式中：A为传播常数，其值恒小于1且大于0；γ为传播常数，由衰减常数α和相位常数β构成，三者之间的关系由下式决定：

γ=α+jβ=

(11)

传播常数反映出了一定能量的衰耗和相位的移动随着行波在输电线路上不断传输而产生，由于输电线路上电阻的存在而产生能量的衰耗，电能按照电磁波的形态在输电线路上传送的本质便有了相位移动。由于线路参数Rm、Lm、Gm、Cm均为已知参数，化简可得

α=

(12)

根据式(12)可计算衰减常数α，α表示入射波和反射波沿线的衰减特性，其单位通常用Np/m。

对于任一频率分量，无论是正向行波分量还是反向行波分量，随着波过程的前进，幅值将减小且相位会滞后，结合式(10)不难看出，随着故障距离的增大，行波的衰减会越加严重，由于行波波头已经变得平缓，故标定波头到达时刻将变得困难，如用小波模极大值标定来进行行波测距的精确度并不理想，而派克变换可以对实时的采样数据进行处理，可用于微弱故障的浪涌检测及波头标定。为展示派克变换对此类微弱故障的检测能力，在半波长输电线路1 500 km处设置A相经500 Ω过渡电阻接地，90°故障角，故障持续时间为5 ms，故障附加网络如图3所示。

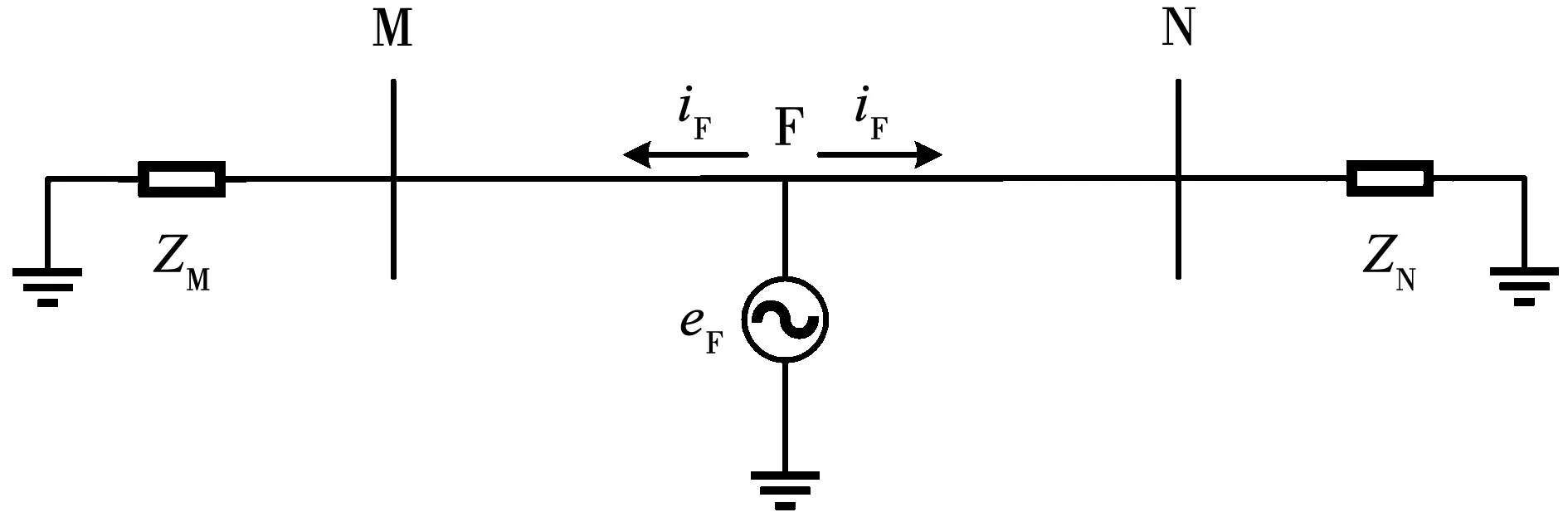
图3 故障附加网络Fig.3 Additional circuits of the fault

派克变换及小波模极大值标定结果如图4所示，通过图4对比不难看出，对于弱故障模式，如过渡电阻大于线路波阻抗或超长线路远端故障，致使观测点故障初始行波变化平缓，对于平缓的故障行波波头的波到时刻，用小波模极大值来对波头进行标定的精确度并不理想，标定时刻将会出现延时。但是线路发生故障后，由于叠加故障附加源，三相电压、电流的幅值及相位会发生变化，经派克变换故障初始波头得到没有延时的放大，因此弱故障模式下，派克变换依然有较高的精确度。

若直接采用id进行故障时刻的标定，可能会因为id的幅值突变量较小或者噪声的影响导致标定失败，因此，引入id的增量cdif及其能量ξdif来解决此问题，定义：

cdif(k)=id(k)-id(k-1)；

(13)

(14)

式中：id(k)表示直轴分量id的第k个采样点；cdif(k)表示id能量增量cdif的第k个值；ΔkEN表示一定时窗内的采样点数，此处选5 ms时窗数据。

图4 两种方式标定波头对比Fig.4 Comparison of two methods calibration the wavehead

将初始行波到达线路两端的时刻分别标记为tM1和tN1，则可按下式计算出故障位置：

(15)

式中：xf为故障位置；l为线路总长度；v为电磁波波速，取v=2.98×108m/s。

3 半波长输电线路长度修正

提高故障定位的精确度一直是国内外学者孜孜以求的目标。实际工程中，由于环境温度、风速、覆冰以及导线的载流量等因素，会导致线路长度发生变化。对于半波长这样的超远距离输电系统来说，每个档距细微的长度变化，扩大到全线数千个档距，可能造成数千米的线路长度误差，这将极大地降低故障定位的精确度。

1)内部因素。

由于输电线路并不是绝对刚体和理想导线，负荷电流和线路电阻导致的热效应会使线路出现热胀冷缩的现象。显然，在实际运行中，线路载流量的不同会导致长度发生不同的变化。导线正常工作时的载流量I可以用摩尔根公式全面的描述[15]，即

(16)

式中

A=πεSD[(δ+ta+273)4-(ta+273)4]。

(17)

式中：αs为导线吸热系数；ε为导线表面辐射系数；二者都取光亮新线为0.23～0.46，发黑旧线为0.9～0.95。

各变量单位及意义如表1所示。

表1 摩尔根公式变量单位及意义

式(16)～式(17)适用于环境温度≤40 ℃，导线温度≤120 ℃，风速0.5 m/s，线径4.2～100 mm情况下。取我国大部地区年平均温度ta=15 ℃，以特高压半波长输电线路8分裂LGJ-500/35型钢芯铝绞线为例，环境温度25 ℃时允许载流量为670 A，此时导线温度约为50 ℃，若某时刻线路故障过载50%，持续过载时间为5 min，此时导线温度将达到115 ℃，比环境温度高约65 ℃。

导线长度和温升之间的关系式为

Δl=lλΔt。

(18)

式中λ为线胀系数，20.9 ℃。若以全线固定档距1 km为例，半波长3 000 km导线将增长Δl=1×20.9×10-6×65×3 000=4.075 5 km。

此外，导线在温度、外力及重力下，会随时间产生永久形变，称之为蠕变，据文献[12],理论上蠕变量为线长的0.3‰～0.5‰，故3 000 km线路蠕变量约为1 km。

2)外部因素。

输电线路在实际运行中的误差还包括勘测误差、弧垂误差及环境温度误差等的影响，据文献[16]的计算，每100 km线路误差总计不超过800 m，假设以上误差均匀分摊至半波长3 000 km全线，则会造成24 km的线路长度误差。

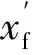
(19)

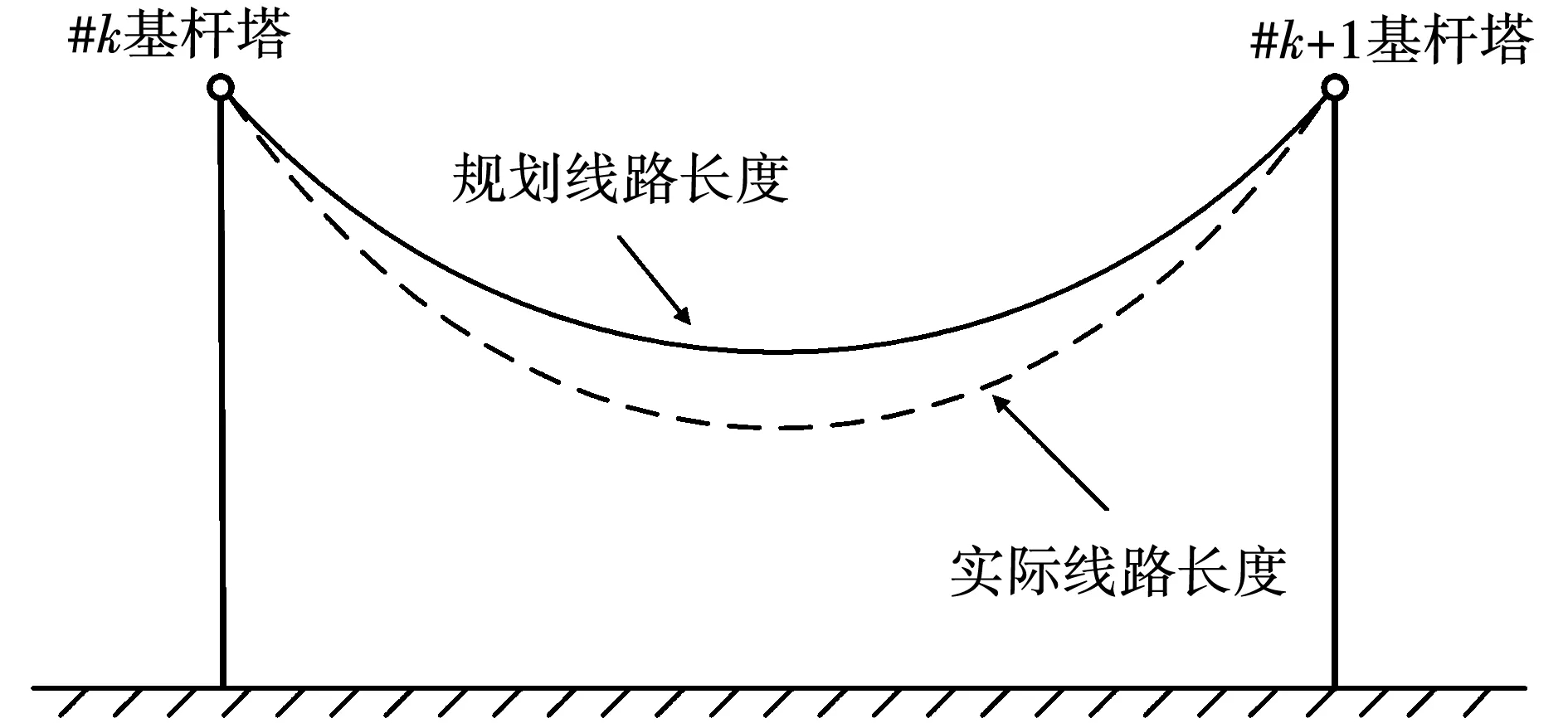
图5 线路长度误差示意图Fig.5 Variation diagram of the line length error

若假定全线以固定档距1 000 m沿线布置3 001个杆塔，杆塔编号为#1～#3001，且假定线路长度在每个档距都均匀变化，则考虑修正线路长度后的测距结果与杆塔号对应关系为

(20)

4 测试与分析

本文采用RTDS搭建半波长输电线路仿真模型，从GTAO口输出仿真数据的模拟信号，再以本课题组研制的录波装置采集信号，形成仿真系统逻辑闭环，最大限度还原真实工况，验证算法可靠性，仿真硬件系统如图6所示。

仿真测试模型如图7所示，参数选用特高压1 000 kV线路参数，设线路均匀换位，两端电源系统，线路全长3 029 km。

以图8所示的晋—南—荆特高压杆塔作为特高压半波长输电线路杆塔，设线路均匀换位，两端电源系统。#1与#3001号杆塔分别位于M、N端母线出口处，其间的规划线路长度为3 000 km，等分为3 000个档距，实际线路长度为3 029 km，仿真采样频率为1 MHz。

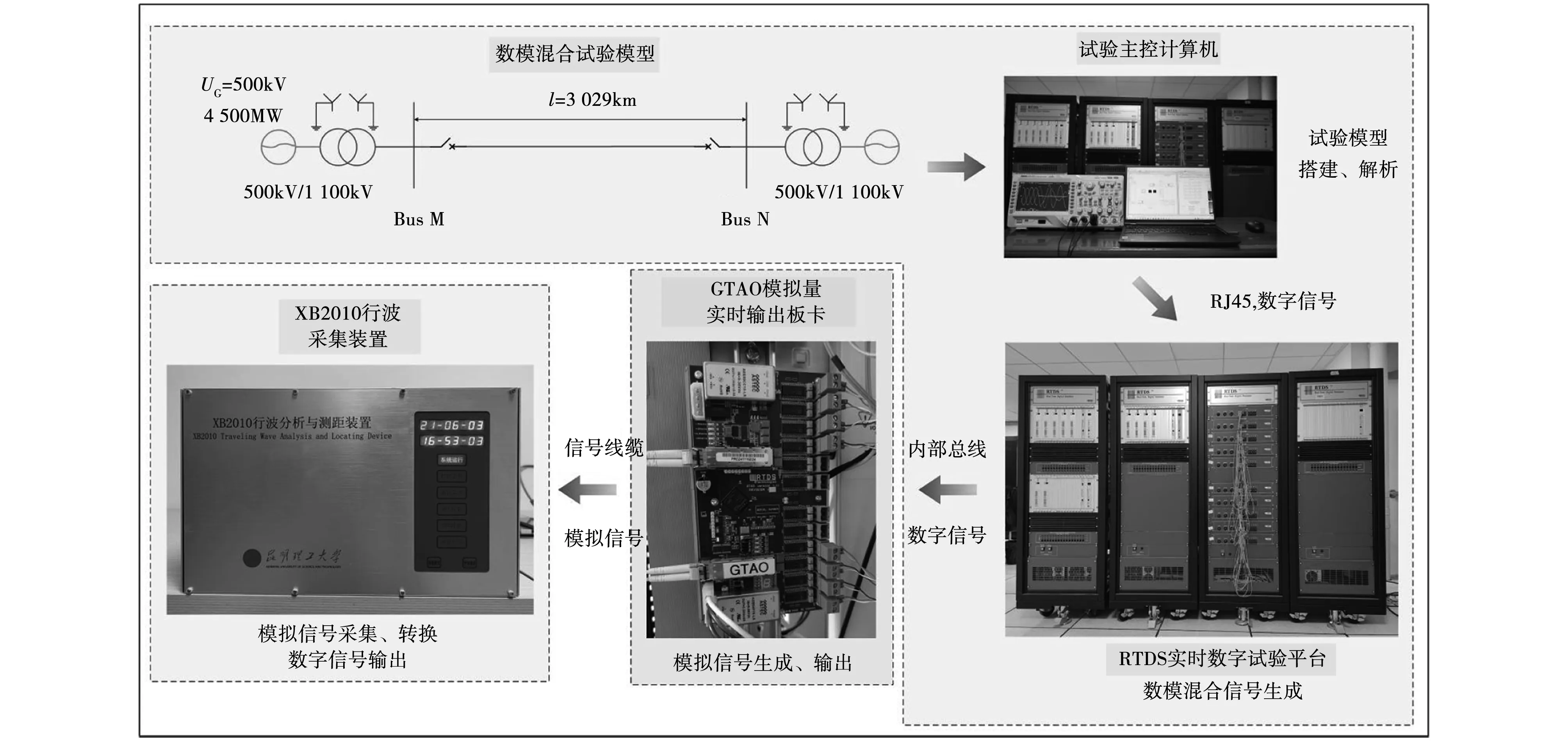
图6 仿真测试系统Fig.6 Simulation system

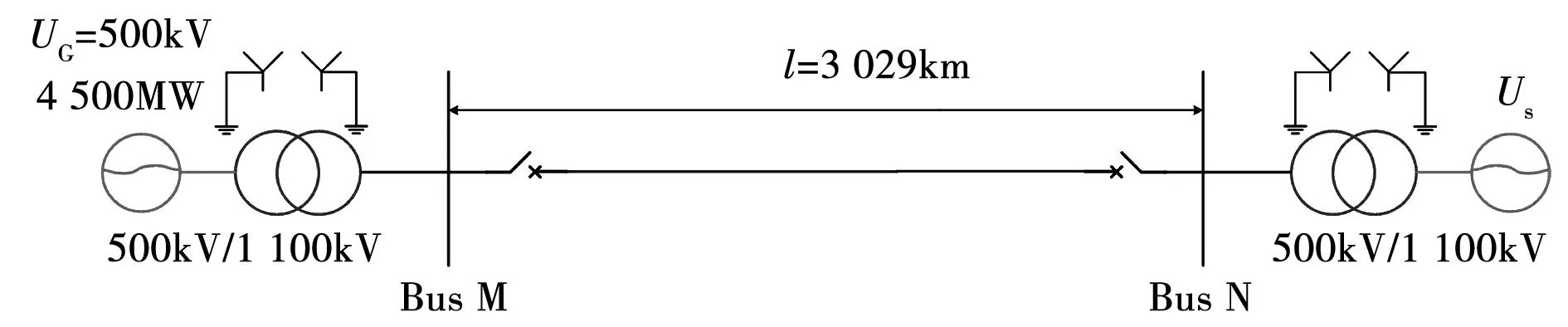
图7 仿真系统模型Fig.7 Model of simulation system

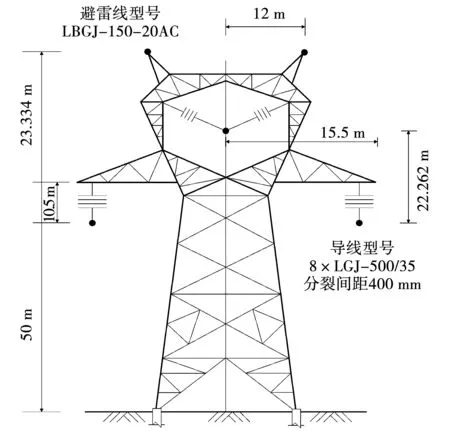
图8 线路杆塔模型Fig.8 Line tower model

算例1 ：M侧母线出口0.1 km(模拟半波长输电线路送端出口)处发生A相金永故障，故障角为70°，波头标定结果如图9所示。

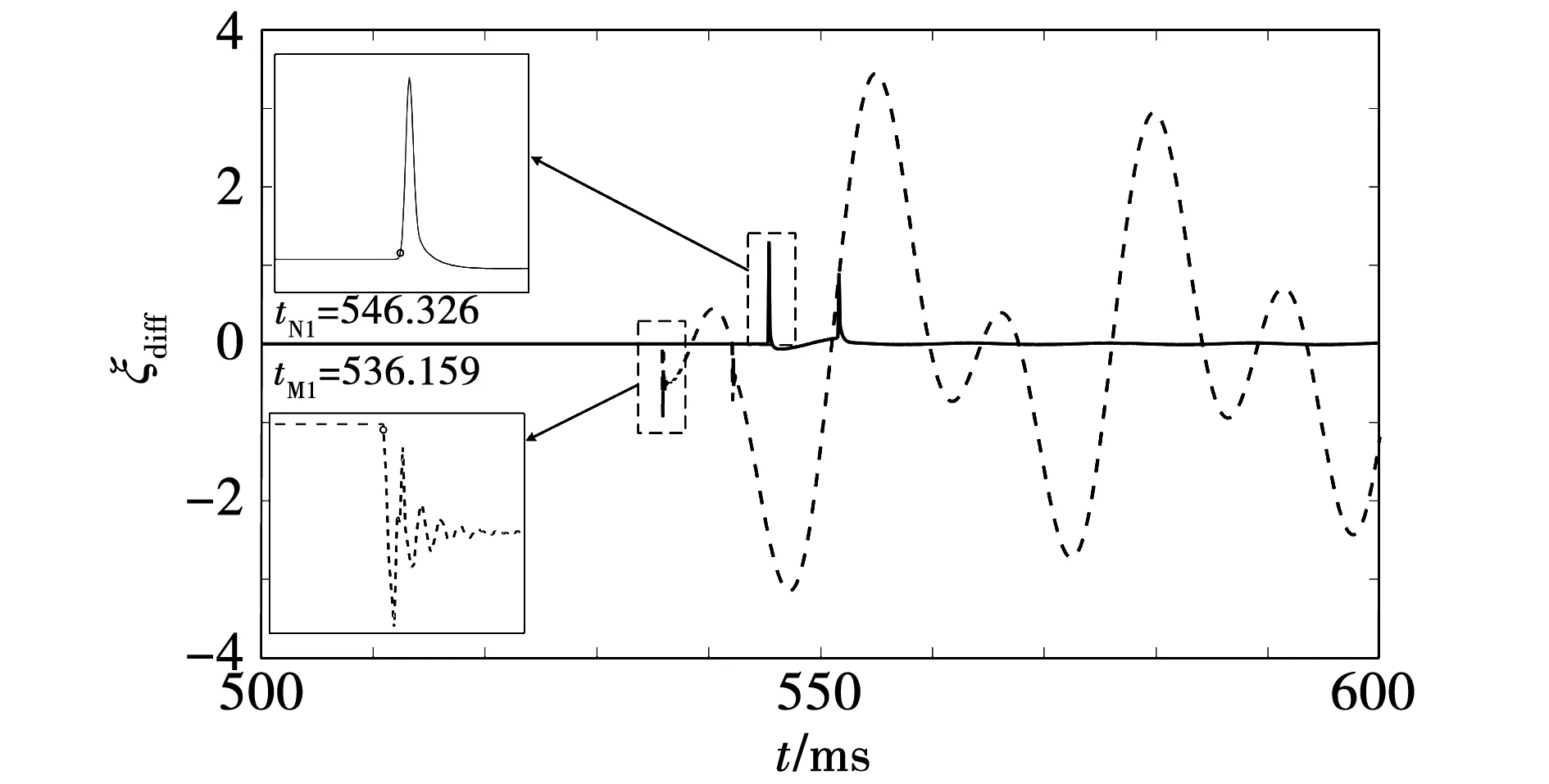
图9 算例1仿真结果Fig.9 Simulation results of example 1

算例2 ：为测试本文所述方法的抗扰能力，在仿真数据的基础上叠加实测的噪声信号，设置故障于1 514.5 km(模拟半波长输电线路中点)处，故障类型为AB相间短路，故障持续5 ms，波头标定结果如图10所示。

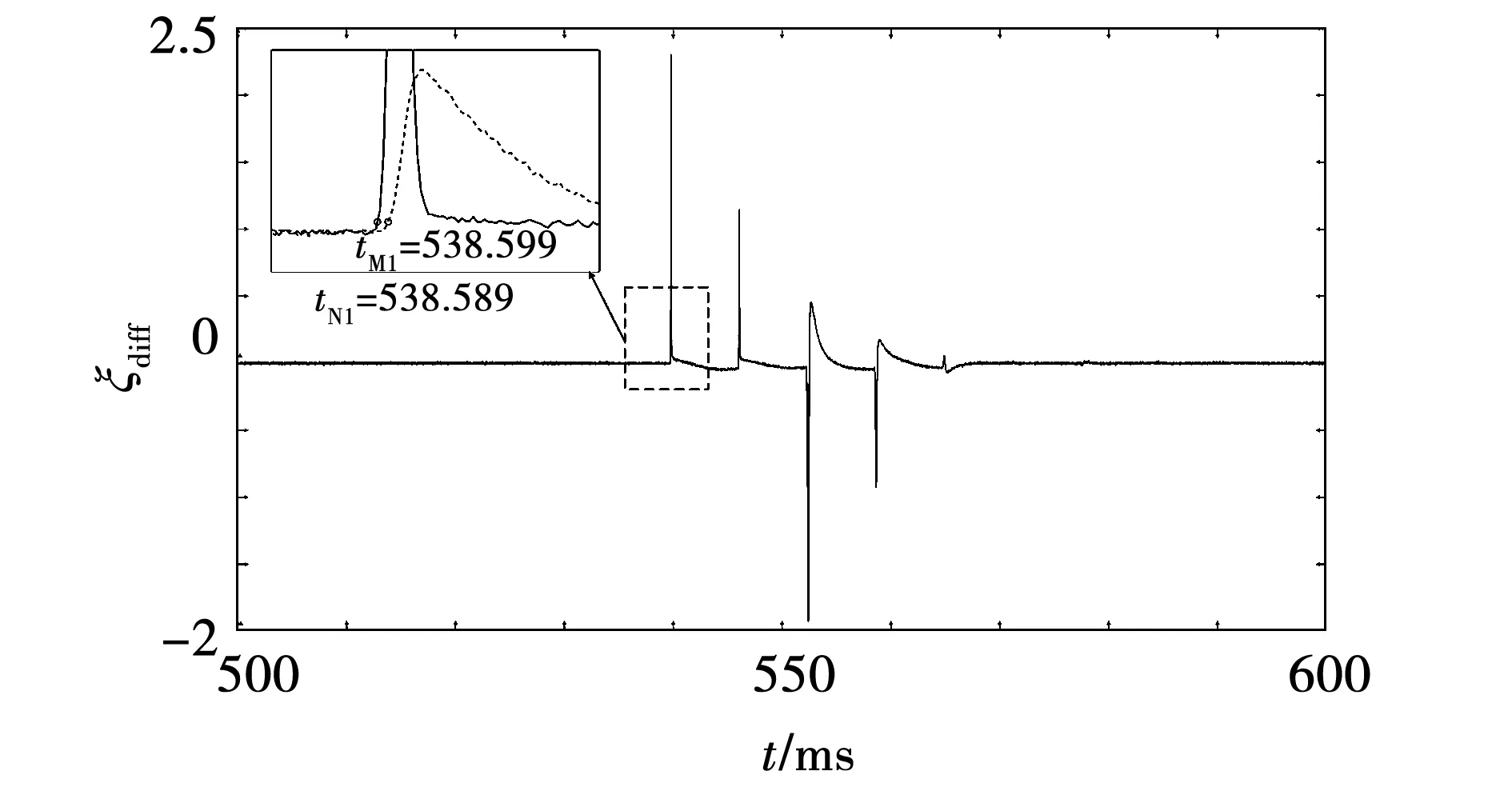
图10 算例2仿真结果Fig.10 Simulation results of example 2

算例3 ：距M侧2 423.2 km(模拟半波长输电线路最严重故障点2 400 km)处，发生A相经300 Ω过渡电阻永久性接地，故障角90°，波头标定结果如图11所示。

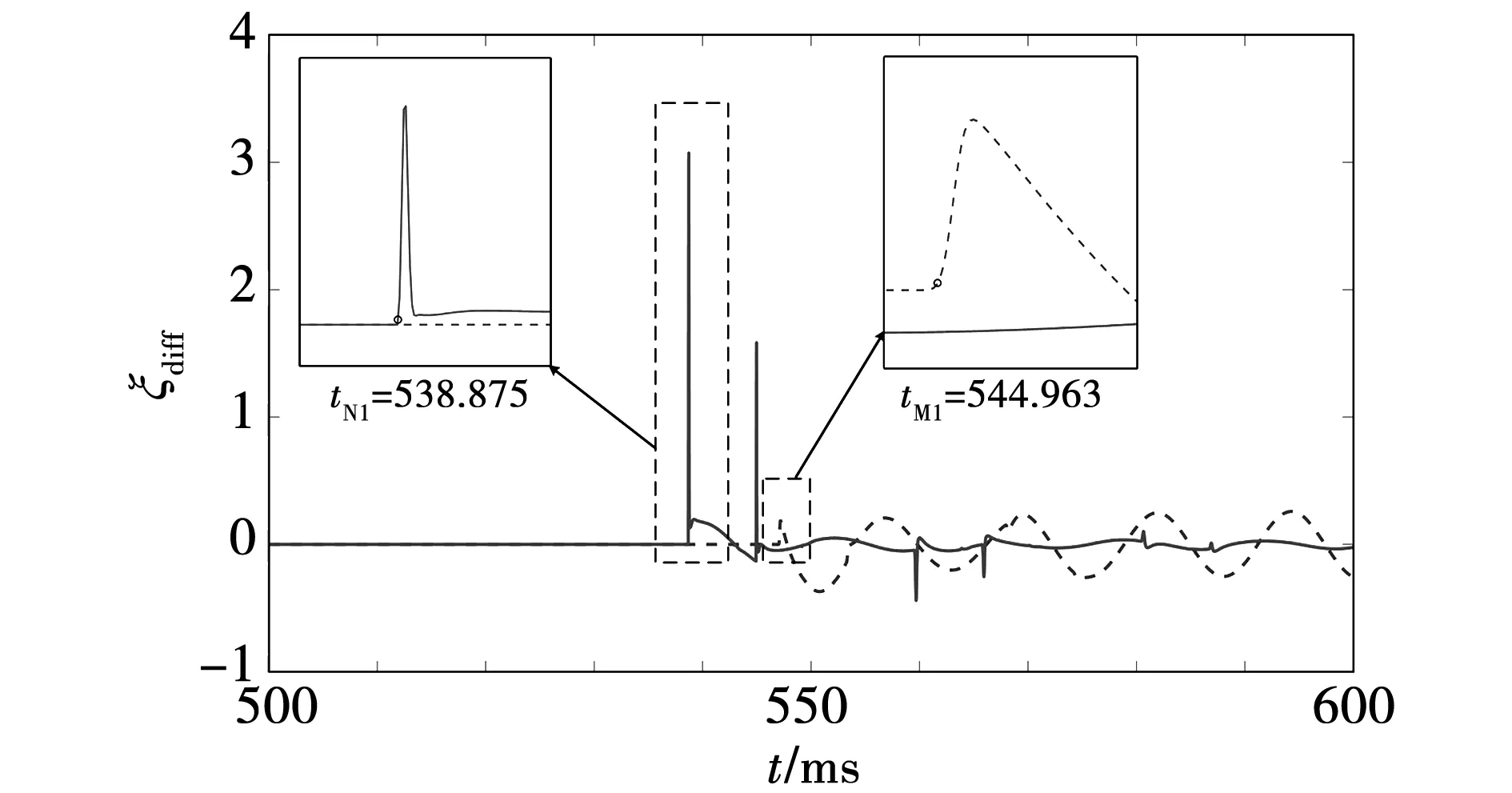
图11 算例3仿真结果Fig.11 Simulation results of example 3

5 结 论

1)半波长输电线路行波色散严重，准确表征波到时刻是行波测距应用于半波长输电线路的难点与关键。本文提出使用派克变换作为标定手段，能够无延时的表征各种类型的行波波头，RTDS仿真结果表明该方法精确度较高，满足超长输电线路故障定位的精确度要求；

2)架空线路会因为气温、载流量、蠕变等因素产生形变，导致电磁波传输的距离与实际线路规划长度不一致，对于3 000 km的半波长输电线路，线路实际长度可能与规划长度相差较大，从而极大地降低故障定位精确度。本文理论分析了线路长度产生变化的原因，计算了一定条件下线路长度的变化量，并且提出了将定位误差归算到以杆塔为基准的方法，在实际工程应用中，可用区外故障来精确计算线路长度，并且以实际杆塔档距为归算依据，可得到较高的定位精确度；

3)本文所述方法，不受故障类型、过渡电阻及故障位置的影响，波头标定算法简单，计算量小。采用RTDS仿真平台结合本团队研发的录波装置验证了该方法的正确性，仿真结果表明，定位精确度不超过0.06%，杆塔偏移不超过2基，具有很好的工程实用性。