基于等效热网络法和CFD法高速永磁同步电机热计算研究

吴胜男， 郝大全， 佟文明

(1.沈阳工业大学 电气工程学院，辽宁 沈阳 110870； 2.沈阳工业大学 国家稀土永磁电机工程技术研究中心，辽宁 沈阳 110870)

0 引 言

高永磁同步电机(high speed permanent magnet synchronous motor，HSPMSM)具有高功率密度、高效率,可直接与负载相连等特点，广泛应用于航空航天、船舶驱动、离心压缩、切削车床、飞轮储能等领域[1-2]。高速永磁同步电机在高转速运行时，在电机内部产生了高频电磁谐波，电机的能量消耗也进一步增大，加上散热问题，电动机的温升问题就凸现了出来。所以，正确的统计分析电动机的温度分布状况对设计电机必不可少。

目前，国内外关于温度场计算常用的方法有基于等效热网络的路算法、基于计算流体动力学(computational fluid dynamics，CFD)场算法以及基于经验公式的有限元场算法[3-7]。韩雪岩等学者采用有限元法对起重机用外转子永磁同步电机的三维瞬态温度场进行了计算[8]。王晓远等学者采用等效热网络发和三维有限元法，以轮毂电机为研究对象，计算了电机在额定状态下的稳态温升，并得到了温升随时间变化曲线[9]。Chen Y等基于三维有限元法和电磁场、流场、温度场多物理场耦合理论，对一台高速永磁同步电机进行了研究[10]。Tong W M等采用双向磁热耦合的方法，对一台非晶合金HSPMSM进行了热分析[11]。丁树业等采用等效热网络法对电机启动时的瞬态温升以及电机稳定状态下稳态温升的时空分布情况进行了详细分析[12]。陈近华等基于计算流体动力学及流固耦合理论，对一台丁胞水冷结构的HSPMSM进行了热分析[13]。

目前，关于电机热计算的研究，尤其是全封闭高速电机，很少考虑到电机内部空气温度分布不均对空气密度、运动粘度、导热系数、动力粘度物理属性的影响。本文基于传热学的基本理论，以一台非晶合金定子水冷HSPMSM为研究对象，建立水冷电机的等效热网络模型，并根据编制的等效热网络程序，计算电机各部件节点的温升；采用CFD的数值方法，考虑电机内空气温度分布对空气密度、比热容、动力粘度以及导热系数的影响，并与恒温下电机内恒定物理属性的温度场计算结果以及转子外表面空气摩擦损耗计算结果进行对比分析；最后，搭建样机温升实验平台，进行温升实验，验证了等效热网络法和CFD法计算结果的准确性。本文为HSPMSM的热计算方面提供一定的借鉴意义。

1 物理模型与损耗

1.1 电机物理模型及参数

本文研究的HSPMSM定子铁心采用非晶合金材料，电机为全封闭结构。永磁体采用内置式“一”字形排列，机壳内部设置螺旋水道，用以消耗电机产生的热量。电机的基本参数如表1所示。

表1 电机参数

电机进行温升计算时，需要对求解域模型做出如下假设：

1)假设电机产生的热量全部由机壳水套中的水和端盖与外界空气的自然对流散热带走；

2)假设电机各部件产生的损耗均布在电机各部件上；

3)绕组端部等效为直线型，定子槽内裸铜等效为一个绝缘实体，定子槽内除了裸铜线外填充的复杂绝缘物质等效为一个绝缘实体，分别用一个等效导热系数替代；

4)考虑机壳与定子铁心之间的装配间隙0.008 9 mm；

5)假设电机内部的热量仅通过热传导和热对流进行换热，忽略辐射传热的影响；

6)忽略了温度分布对损耗的影响，假设电机的各固体部件的材料属性不随温度变化。

基于以上基本假设，根据电机的对称结构取圆周方向1/2为求解域模型，建立电机的三维求解域模型。电机物理模型如图1所示。

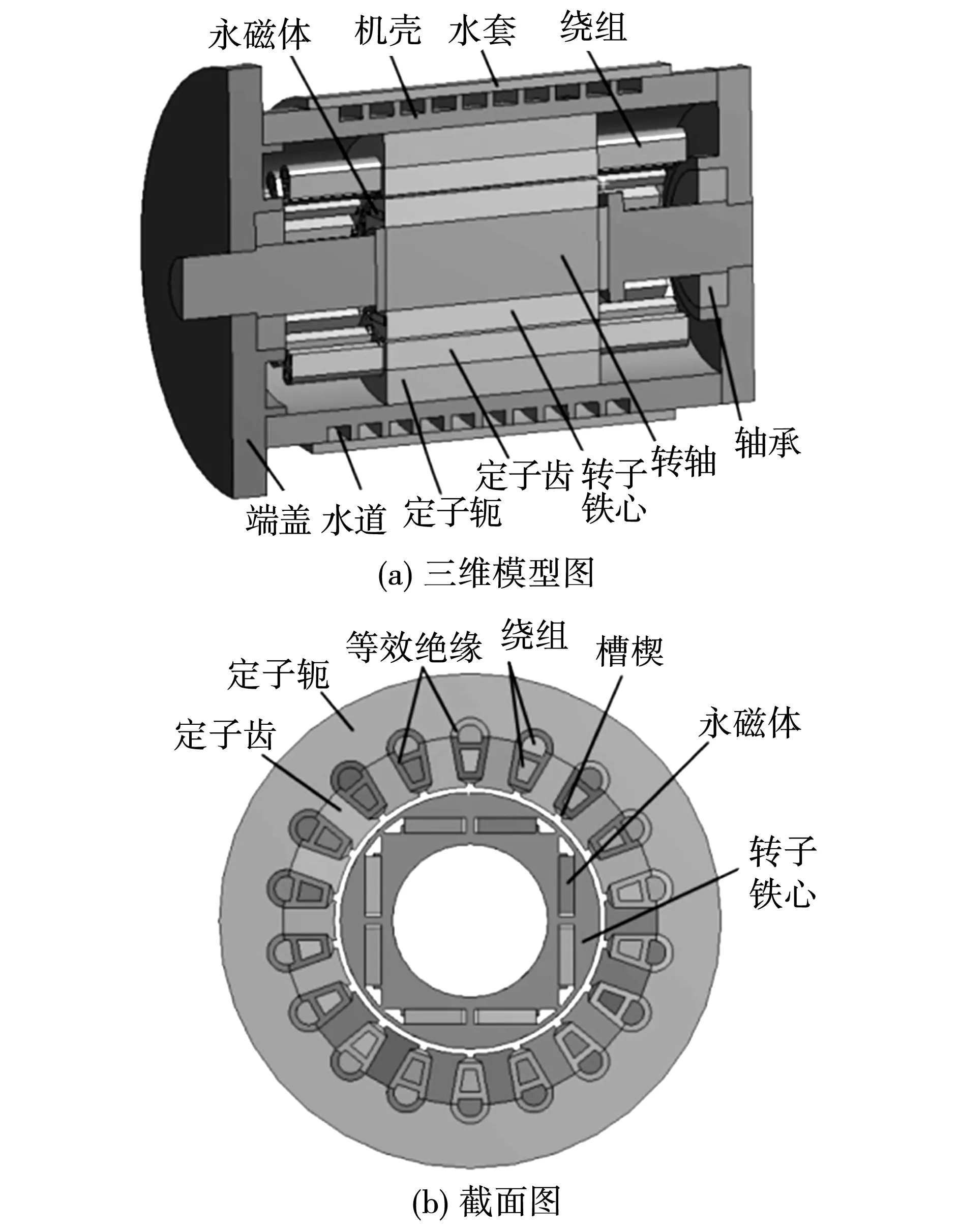
图1 物理模型Fig.1 Physical model

1.2 损耗分析

表2为15 kW永磁体同步电动机采用变频器供电时的各部分损耗值。其中，假设转子外表面光滑，转子外表面的空气摩擦损耗采用Fluent软件计算为27.8 W，假设均匀分布在转子铁心外表面上。

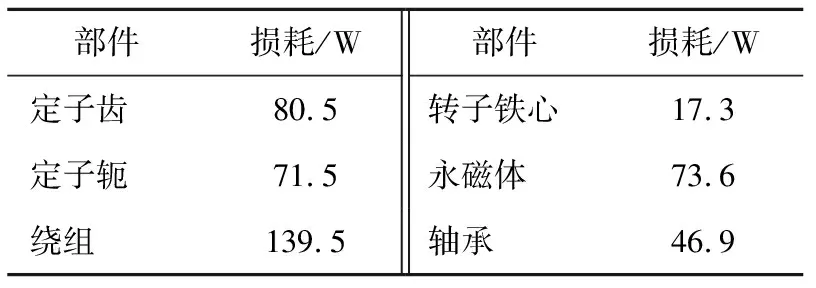
表2 电机各部件损耗

2 等效热网络法温升计算

根据电机的结构及材料属性，进行网格节点划分，然后求解不同节点之间的热阻，将电机各部分损耗均匀加载在各个网格节点上，根据传热学的基本理论，建立热平衡方程组[14]。最后采用MATLAB编程求解，得出各个网格节点的温升。

2.1 等效热网络模型

根据电机的结构及材料属性建立电机的全域等效热网络模型，如图2所示。定子铁心和转子铁心沿轴向均匀划分为3个节点，机壳、定子绕组和转轴划分为5个节点，左右轴承、左右端盖和左右端腔空气各划分为1个节点，不同节点对应的电机部件如表3所示。

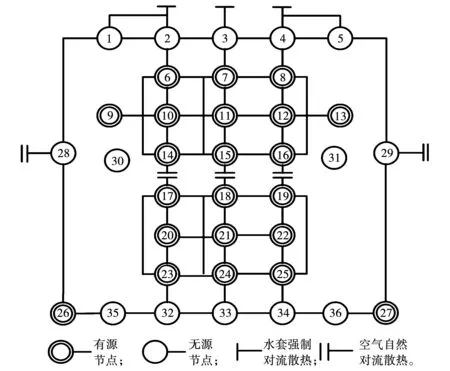
图2 等效热网络模型Fig.2 Equivalent thermal network model

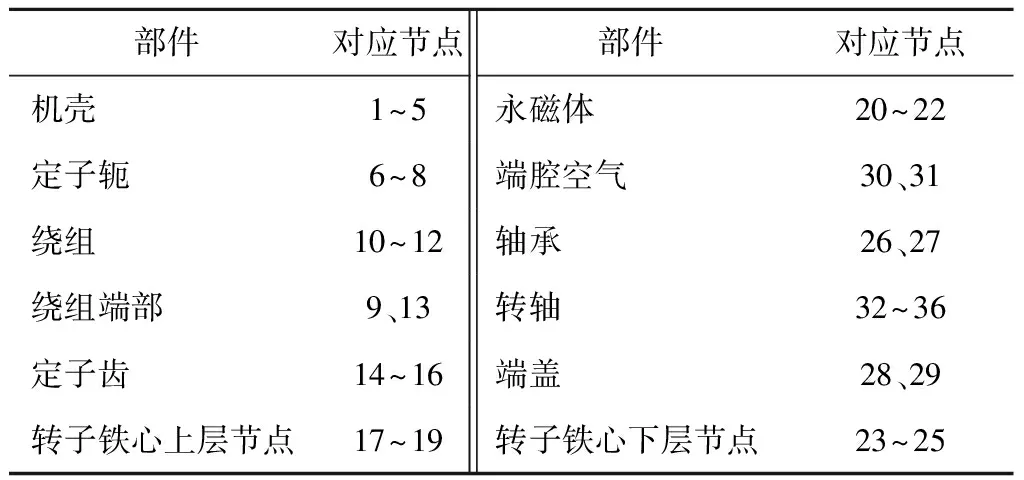
表3 电机各部件对应节点

2.2 热阻分析

热阻可以分为导热热阻、对流散热热阻和辐射热阻[15]。电机内部通过辐射传递的热量很小，在进行电机热计算时可忽略通过热辐射传递的热量。

导热热阻的计算方程为

(1)

式中：A为固体材料的热量传递面积，m2；L为固体材料的热量传递长度，m；k为固体材料的导热系数，W/(m/K)。

对流散热热阻的计算方程为

(2)

式中hc为对流散热系数，W/(m2/K)。

根据电机各个部件及不同材料属性，计算各个节点之间的传热距离及传热面积，从而计算出各个节点之间的热阻。电机内不同材料的导热系数如表4所示。

表4 电机各部件导热系数

2.3 计算结果

根据热平衡原理，分别构建热导矩阵G、节点温度矩阵T、热源矩阵W，其中，热导为热阻的倒数，热导矩阵G为36×36阶稀疏方阵，节点温度矩阵T、热源矩阵W为36×1阶矩阵。列出等效热平衡方程

GT=W。

(3)

各个节点温升计算结果如表5所示。从表5可以看出，电机最高温升位于永磁体，为56.7 K，最高温升位置位于永磁体轴向中间位置。定子最高温升位于端部绕组，为54.6 K，定子轭和定子齿最高温升分别为18.6和25.8 K，最高温升位置位于定子轭和定子齿轴向中间位置。

3 CFD法温升计算

采用CFD法计算电机的各部件温升，取电机圆周方向1/2模型为求解域，如图1(a)所示。螺旋水道内冷却介质为水，入口速度0.3 m/s，入口水温288.2 K，环境温度设置为300 K。气隙与转子接触面、转子铁心与端腔空气接触面为旋转面，指定旋转速度为电机的额定旋转速度。模型剖面设置为周期边界。

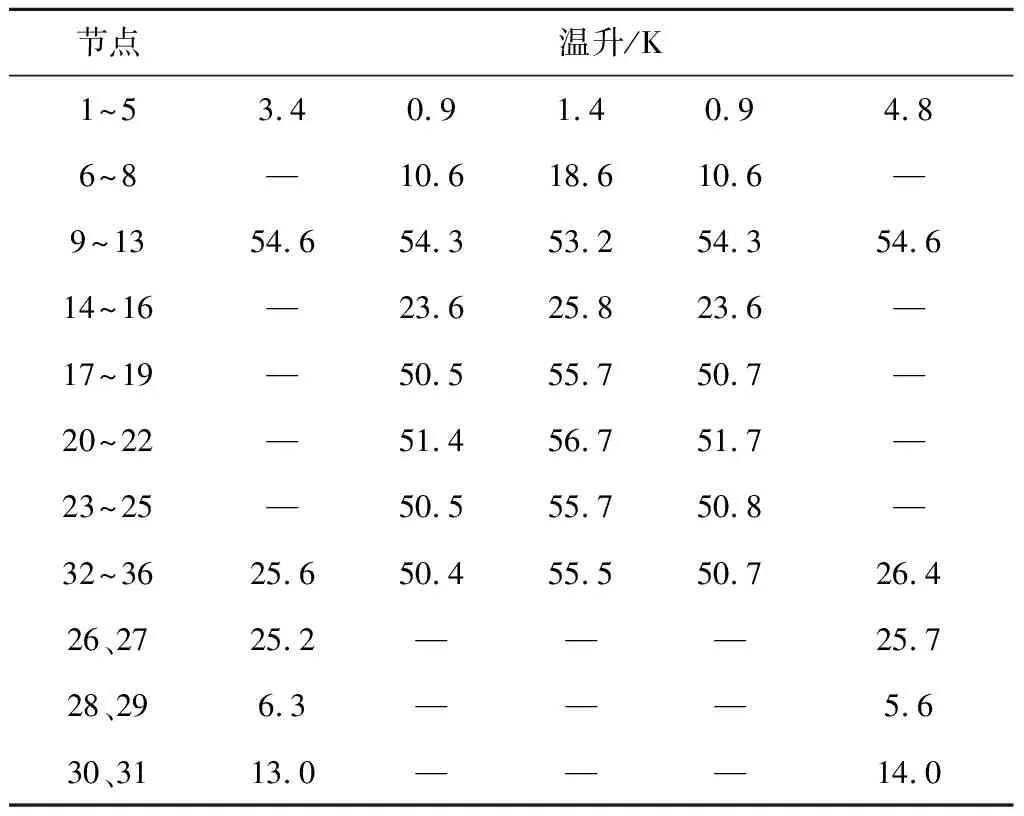
表5 电机各节点温升

3.1 机内空气施加恒温物理属性

电机内空气的密度、比热容、导热系数、动力粘度按照恒温80 ℃施加恒定值，进行温度场求解。求解域温度分布云图如图3所示。

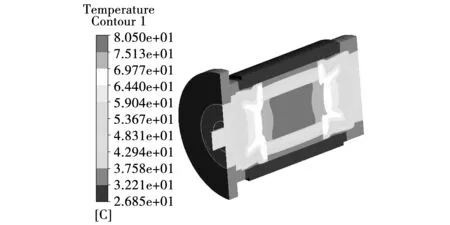
图3 求解域温度分布Fig.3 Temperature distribution of solution domain

从图3中可以看出，电机的转子最高温升位于永磁体中间位置，为52.2 K，转子铁心略低，为51.9 K。转子区域中间位置温升最高，且存在一定面积的高温区域，温度依次向两端递减。定子最高温升位上层端部绕组，为53.7 K，这是因为上层绕组靠近气隙位置，与下层绕组相比距离机壳水套较远，热阻相对大，散热效果较差。

电机内部空气温度分布不均匀，气隙处轴向中间位置和端部绕组附近空气温度较高，沿轴向向两端端腔温度分布逐渐降低。机内空气最高温度位于转子外表面，为78.3 ℃，气隙平均温度为62.4 ℃，机内空气最高温差达到49.1 K。

3.2 机内空气施加变温物理属性

不同温度下空气的密度、比热容、导热系数、动力粘度如表6所示[16]。由于空气物理属性随温度变化明显，电机内空气温度分布不均，因此采用CFD法计算电机温升时，考虑了电机内不同位置空气温度对其物理属性的影响。

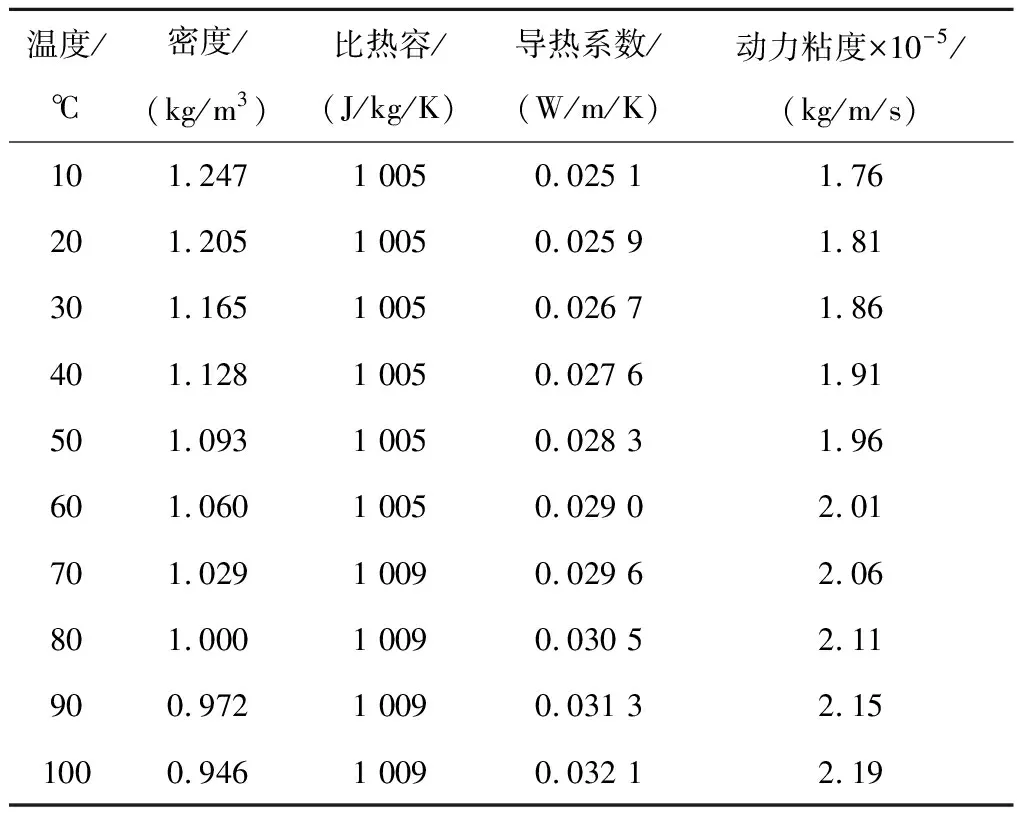
表6 不同温度下空气的物理属性

基于最小二乘法原理对不同温度下空气的密度、导热系数、动力粘度进行曲线拟合，不同温度下空气的比热容用分段函数表示。

温度对空气密度的影响如下：

ρ(T)=-4e-24T6+5e-12T5-1e-9T4+

1e-7T3+8e-6T2-0.0045T+1.2913。

(4)

温度对空气导热系数的影响如下：

λ(T)=-6e-14T6+1e-11T5-1e-9T4+

2e-8T3+1e-6T2-5e-5T+0.0245。

(5)

温度对空气动力粘度的影响如下：

η(T)=-9e-19T6+6e-15T5-7e-12T4+

5e-9T3-4e-6T2+0.0051T+1.711。

(6)

温度对空气比热容的影响如下：

(7)

式中：ρ(T)为不同温度下空气的密度，kg/m3；λ(T)为不同温度下空气的导热系数，W/(m/K)；η(T)为不同温度下空气的动力粘度，kg/(m/s)；cp(T)为不同温度下空气的比热容，J/(kg/K)；T为空气的温度，℃。

图4给出了机内空气物理属性随迭代过程中温度变化的流程图。对电机内空气施加变温下密度、比热容、导热系数、动力粘度，计算电机的温度分布，求解域温度分布云图如图5所示。电机转子最高温升位于永磁体永磁体中间位置，为54.9 K，转子铁心略低，为54.7 K。转子区域中间位置温升最高，且存在一定面积的高温区域，温度依次向两端递减。定子最高温升位上层端部绕组，为53.6 K。

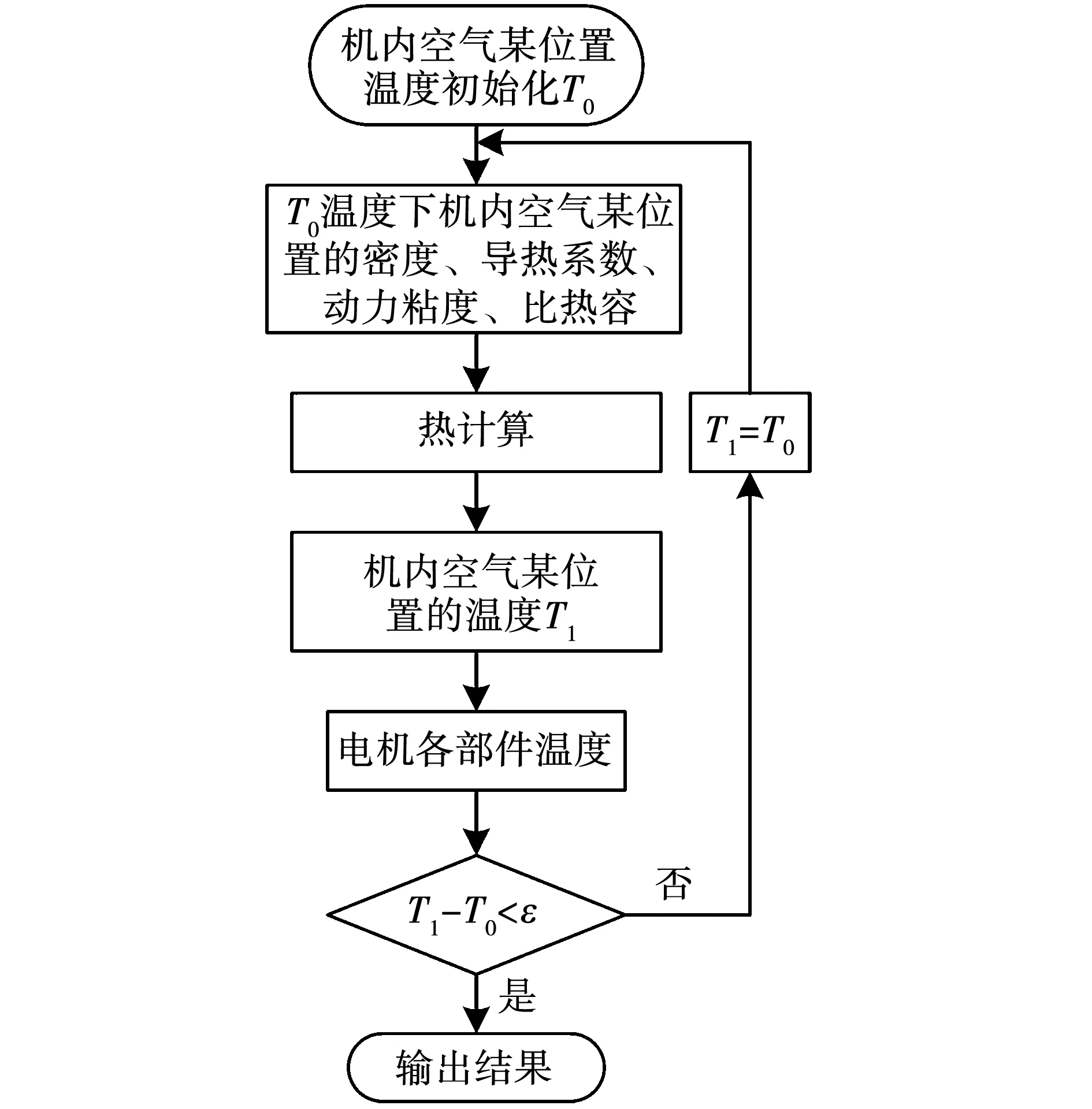
图4 机内空气物理属性与其温度的相互影响Fig.4 Interaction between the physical properties of air and its temperature

图5 求解域温度分布Fig.5 Temperature distribution of solution domain

3.3 机内空气施加恒温与变温物理属性对比分析

两种情况下各部件温升对比如表7所示，其中，情况1为施加恒温下(80 ℃)电机内空气的物理属性的各部件温升，情况2为考虑机内空气温度分布，施加变温下电机内空气的物理属性的各部件温升。

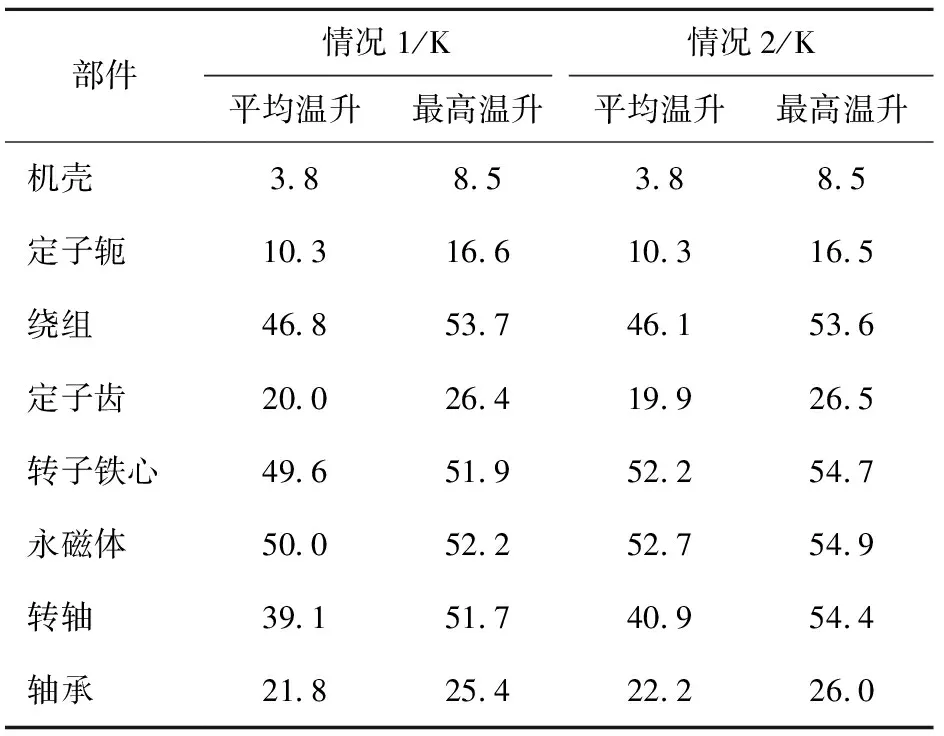
表7 两种情况下电机各部件温升对比

从表7中可以看出，情况2与情况1相比：定子区域最高温升和平均温升相差不大，转子区域最高温升和平均温升稍高。情况2永磁体和转子铁心最高温升较情况1分别高2.7和2.8 K，平均温升均高2.7和2.6 K，永磁体和转子铁心最高温升相差4.9%和5.1%，平均温升相差5.1%和5.0%；情况2转轴和轴承最高温升较情况1分别高2.7和0.6 K，平均温升分别高1.8和0.4 K，转轴和轴承最高温升相差5.0%和1.5%，平均温升相差4.4%和1.8%。这是因为气隙最高温度为78.3 ℃，并未达到80 ℃，并且气隙平均温度为62.4 ℃，变温下气隙处的导热系数与比热容较恒温80 ℃小，因此转子向机壳水套的传热性能变差，导致的转子的最高温升和平均温升较高。

两种情况下求解域某截面温度分布云图如图6所示。转子最高温升区域位于永磁体中间位置，定子最高温升区域位于绕组端部，从图中可以看出，情况2与情况1相比，转子高温区域面积明显增加。

根据文献[17-18]，转子外表面空气摩擦损耗可由下式确定：

(8)

P=kmCfρπω3r4l。

(9)

式中：Cf为摩擦系数；τ为转子外表面的剪切应力，Pa；ρ为空气的密度，kg/m3；v为转子的线速度，m/s；km为转子外表面的粗糙度系数，当转子外表面光滑时，km=1；ω为转子的旋转角速度，rad/s；r为转子的半径，m；l为转子的轴向长度，m。

情况1转子外表面的空气摩擦损耗为28.9 W，情况2转子外表面的空气摩擦损耗为27.8 W，两种情况下空气摩擦损耗相差4.0%，因此在利用Fluent计算电机的空气摩擦损耗时，需要考虑电机内部温度分布不均造成的空气物理属性的变化。

图6 求解域某截面温度分布Fig.6 Temperature distribution of a section in solution domain

4 实验验证

为检验等效热网络法和CFD法计算结果的正确性，建立了样机的温升实验平台，以检测电机的温升。对该电机在20 000 r/min下进行了温升实验,在绕组端部和轴承内埋了热敏电阻，用以测量绕组端部与轴承的温升。电机的样机和温升实验平台如图7所示。表8给出了绕组端部温升与轴承温升实验值与计算值，其中，等效热网络法端部绕组和轴承温升计算值误差在4.2%和2.3%，CFD法端部绕组和轴承温升计算值误差在2.3%和1.1%，计算误差在合理范围内。实验结果证明了等效热网络法和CFD法计算的准确性。

图7 样机与温升实验平台Fig.7 Prototype and temperature rise experimental platform

表8 两种情况下电机部件温升对比

5 结 论

本文采用等效热网络法和CFD两种方法，对一台非晶合金定子HSPMSM进行了热分析，并进行了实验验证，证明了等效热网络法和CFD法计算结果的准确性，为HSPMSM的热计算与空气摩擦损耗的计算提供参考。可以得出以下结论：

1)通过等效热网络法计算电机各个节点的温升，最高温升位于永磁体中间位置，为56.7 K，定子最高温升位于绕组端部，为54.6 K；采用CFD法计算电机的温度场，机内空气施加恒温物理属性后，永磁体最高温升为52.2 K，端部绕组最高温升为53.7 K，最高温升位于端部绕组；机内空气施加变温物理属性后，永磁体最高温升为54.9 K，端部绕组最高温升为53.6 K，最高温升位于永磁体，与等效热网络法最高温升位置一致，证明了机内空气施加变温物理属性更接近实际。

2)与机内空气施加恒温物理属性相比，机内空气施加变温物理属性后，对气隙传热能力影响较大，永磁体和转子铁心最高温升分别上升了4.9%和5.1%，并且转子高温区域面积增大；对气隙运动粘度的影响较大，在转子外表面光滑情况下，转子空气摩擦损耗下降了4.0%。