基于动态相量法的三相双有源桥直流变换器闭环系统建模与稳定性分析

钟庆，梁铭，赵宇明，王钢，汪隆君

（1.华南理工大学电力学院，广州 510640；2.深圳供电局有限公司，广东 深圳 518000）

0 引言

随着人类对可再生电源的探索，大量分布式电源接入电网，分布式电源和储能系统的可靠接入方式成为当前智能电网构建的重要目标之一。相比于可再生能源的交流并网方式，直流并网方式的要求更低而且稳定性更高，具有较强的故障穿越和隔离能力[1-2]。这使得不同电压等级和功率容量之间的直流电能在直流电网、分布式电源、负荷之间流动，双向DC/DC 变换器作为直流电能传递的核心装置从而倍受关注[3-5]。双向DC/DC 变换器的拓扑多样，其中双有源全桥直流变换器以其控制简单、具有电气隔离、开关管电压电流应力较小等优点得到广泛认可[6-7]。三相DAB 直流变换器相比于单相DAB 直流变换器，拥有更高的功率密度和传输效率，适用于中、高功率场合，逐渐成为近些年研究的热点[8]。

在对DAB 直流变换器的控制方面，有单移相（single phase shift，SPS）[9]、双移相（dual phase shift，DPS）[10]、扩展移相（extend phase shift，EPS）[11]、三重移相（triple phase shift，TPS）[12]等控制策略。SPS 控制虽然控制灵活度较低，但由于控制简单、易于实现的特点而被广泛采用。其余控制策略的控制自由度较高，但复杂度也相对提升，部分控制参数较难确定，实现起来比较困难。

为了设计闭环控制器和分析系统稳定性，需要建立DAB 直流变换器的数学模型。动态相量可将原始时域信号分解成基频信号与高次谐波信号，描述了原始时域波形近似的包络线，可精确反映原始波形的动态特征。文献[13-14]给出了使用动态相量对电压源型换流器（voltage source converter，VSC）进行建模的过程。DAB 直流变换器可视为两个VSC 的连接，故常规VSC 的建模方法对DAB 变换器仍适用。文献[15]使用动态相量建立了三相DAB直流换流器的多频模型，但是建模部分仅涉及开环情况，未将闭环控制器考虑到模型中。

为此，本文建立了SPS 控制策略下的三相DAB直流变换器的动态相量模型，建模中考虑了闭环控制器，推导得到基于动态相量的小信号模型，根据小信号模型系统矩阵的特征值判断闭环系统的小信号稳定性，研究了控制器参数变化对系统稳定性的影响。最后通过仿真实验，对稳定性分析结果进行验证。

1 三相DAB直流变换器动态相量模型

1.1 动态相量法的概念

动态相量法是一种以时变傅里叶分解为基础的平均值法，主要将时域中快速变化以T为周期的时域信号在时间间隔τ∈(t-T,t)上表示为时变傅里叶级数的形式，公式为

第k次傅里叶系数为

定义x k(t)为第k阶动态相量，根据时变傅里叶级数的阶数来定义动态相量的阶数。动态相量法的本质是在宽度为T的时间窗内，建立以动态相量为系数的时变傅里叶级数，而时变傅里叶级数则是根据滑动的时间窗在时间轴上移动而分解计算出来的。

1.2 变换器的拓扑结构

图1 给出了三相DAB 直流变换器简单闭环系统的拓扑结构。为便于分析，将TN视为变比为N:1的高频理想变压器，忽略其励磁电感，将漏感归算到一次侧。La、Lb、Lc为交流侧三相电感与变压器漏感之和的等效电感，Ra、Rb、Rc为开关电阻、电感电阻、变压器电阻之和的等效电阻。va1、vb1、vc1和va2、vb2、vc2为两侧三相全桥的交流相电压，ia、ib、ic为变压器一次侧相电流。v1和v2分别为DAB 变换器输入侧和输出侧的直流电压，ii和io分别为一次侧和二次侧的直流电流，i1和i2为流入变换器与流出变换器的电流，Cin、Co为输入和输出侧电容。vref为输出电压参考值。D为移相占空比，表示两侧全桥的同一相开关函数的相位之差与周期的比值。

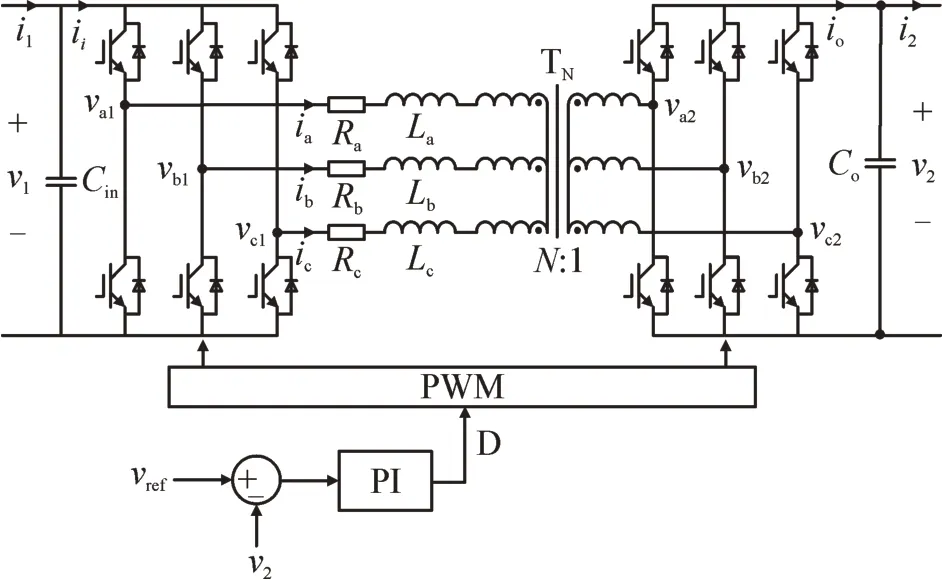
图1 三相DAB直流变换器的拓扑结构Fig.1 Topology of three-phase DAB DC converter

在SPS 控制策略下，令各开关驱动信号的占空比均为0.5，a、b、c 三相开关驱动信号各相差120°。当D＞0 时，功率方向由v1侧流往v2侧；当D＜0 时，功率方向由v2侧流往v1侧。由于DAB 变换器的功率流动具有对称性，本文在v2侧接入负载电阻，针对D＞0 情况进行分析。

1.3 状态空间模型

根据图1 的三相DAB 直流变换器拓扑结构，假设交流侧三相电路对称且对称调制，Ra=Rb=Rc=R，La=Lb=Lc=L，负载电阻为RL。

对于变压器一次侧的交流回路，各相电流满足为

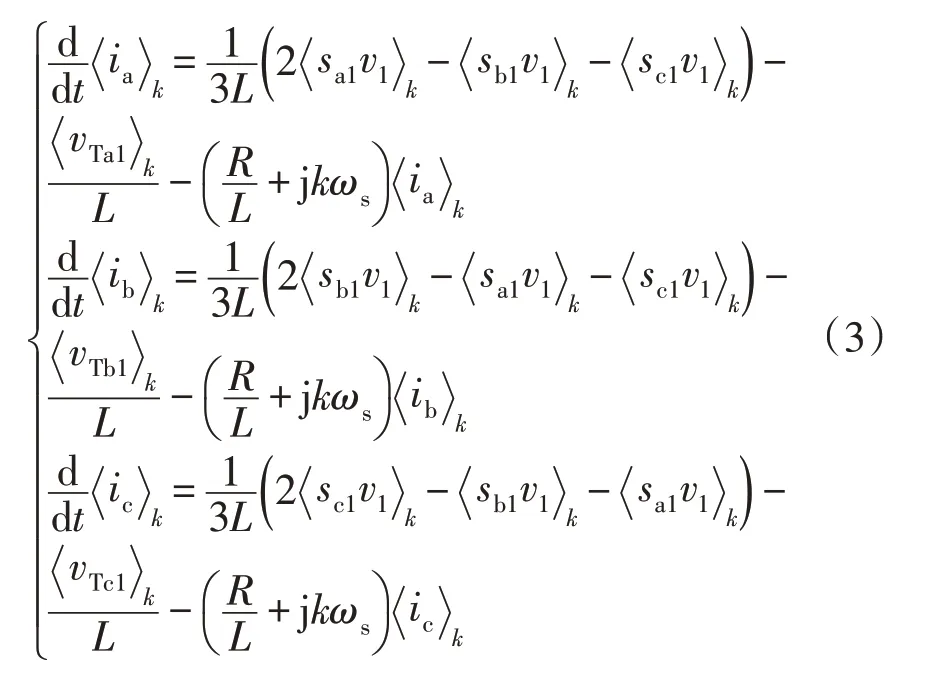
式中：vTa1、vTb1、vTc1为变压器一次侧相电压；ωs为开关信号的角频率，以此作为动态相量的基频；sa1、sb1、sc1为变压器一次侧换流器的三相开关函数。

由变压器一二次侧电压电流关系，有公式为

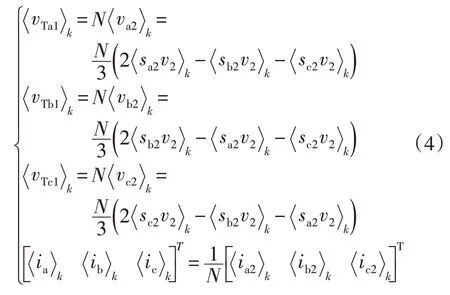
式中，sa2、sb2、sc2为变压器二次侧换流器的三相开关函数。

变压器二次侧换流器的直流侧电压满足公式为

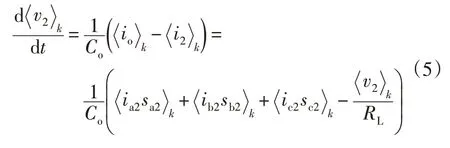
对于闭环控制部分，定义电压环PI 调节器的积分部分输出为状态变量xdc，则有公式为

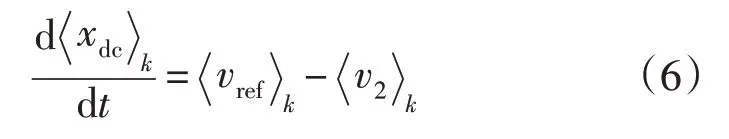
PI 控制器的输出为移相比，其公式为

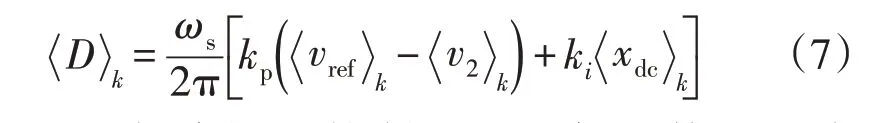
式中，kp、ki分别为PI 控制器的比例系数和积分系数。

SPS 控制模式下两侧三相开关驱动信号均为相位互差120°、占空比为50% 的方波，根据式可计算得到两侧开关函数的k阶动态相量，以A 相为例有：

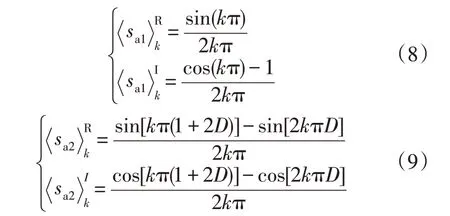
为便于模型的建立与求解，假设输入电压v1为恒定的理想直流电源，其值为V1；vref只有零阶分量，其值为Vref；v2的动态分量极小，为简化分析忽略高阶分量，假设只有零阶分量，即

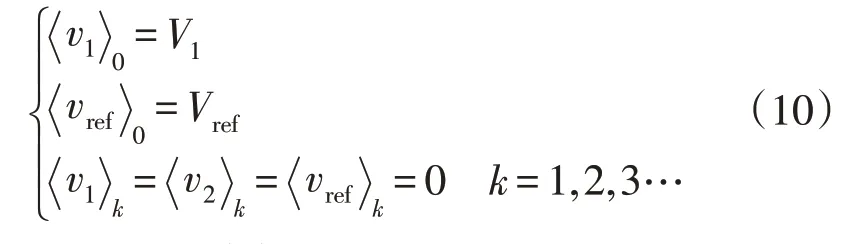
令x和u分别作为系统的状态变量和输入变量，具体公式为

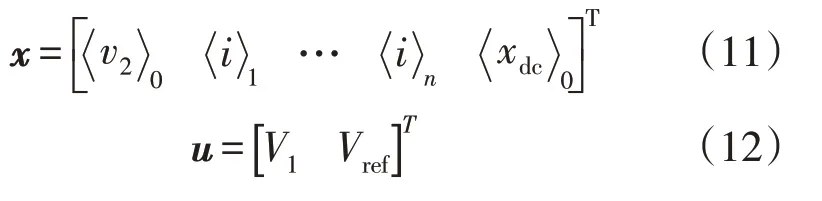
式中，n为所考虑的动态相量总阶数。

i k形式如下：

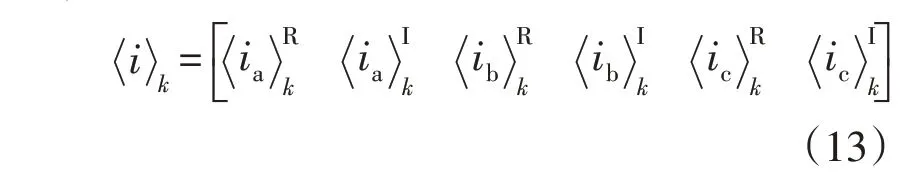
根据式和式所选择的状态变量和输入变量，得到状态方程的矩阵形式为

系统矩阵A和输入矩阵B分别为

矩阵A和B中元素AL,k、AR,k、Hk、Bk（k=1，2，…，n）的具体形式参见附录。

2 三相DAB直流变换器的稳定性分析及小信号模型

2.1 稳定性分析

根据李雅普诺夫第一法，可以通过系统状态方程的解来判别系统的稳定性。对于线性系统，求解出特征方程的根即可作出稳定性判断。对于非线性系统，则可以通过线性化的方法，取其一次近似得到线性化方程，然后再根据其特征值来判断系统的稳定性[16]。

由式（14）所示的状态方程表示的系统为非线性系统，用一组同维矢量函数来表示，公式为

设xe、ue为其平衡状态，为讨论系统在平衡状态处的稳定性，将非线性矢量函数f（x，u，t）在邻域内展开成泰勒级数，公式为

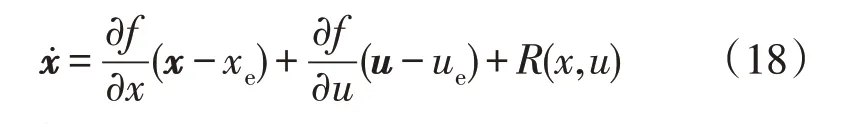
如果令Δx=x-xe和Δu=u-ue，并取式（18）的一次近似式，可以得到系统线性化的小信号模型，公式为

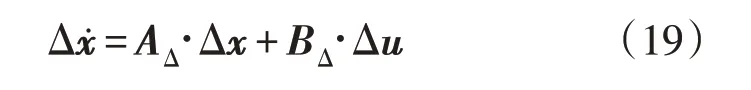
式中

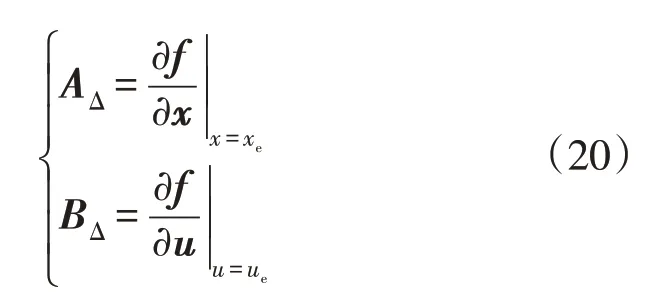
在式（19）的基础上，若小信号模型中的AΔ矩阵没有实部为零的特征值，则非线性系统的稳定性可以完全由线性化后得到的小信号模型的稳定性来决定。如果AΔ的所有特征值实部都为负，系统则是渐进稳定的；如果AΔ的特征值至少有一个实部为正，系统则是不稳定的；如果AΔ的特征值至少有一个实部为零，而其他特征值的实部均为负时，系统为临界稳定状态。

2.2 小信号模型

为得到三相DAB 直流变换器闭环系统的小信号模型，对以下变量引入小信号，公式为分别为小信号值；

将式（14）进行泰勒展开后忽略二阶及以上高阶分量，得到式（19）所示的小信号模型。小信号模型的状态变量和输入变量分别为

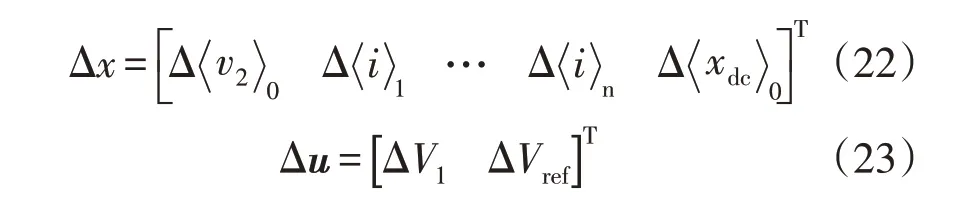
其中，

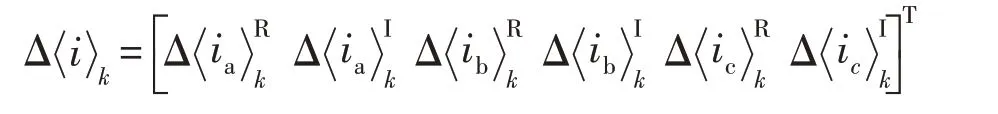
小信号模型的系统矩阵AΔ和输入矩阵BΔ为

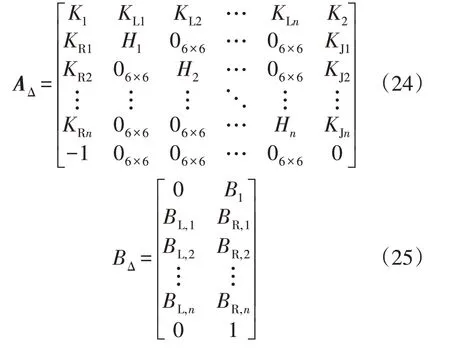
矩阵AΔ和BΔ中元素K1、K2、KL,k、KR,k、KJ,k、B1、BL,k、BR,k（k=1，2，…，n）的具体形式参见附录。

3 分析与验证

3.1 参数设置

为验证使用本文所建模型分析系统小信号稳定性的正确性，对表1 所示三相DAB 直流变换器参数模型进行分析。

表1 三相DAB直流变换器参数Table 1 Parameters of three phase DAB converter

3.2 特征值分析

基于前文推导的三相DAB 直流变换器小信号模型，分析其系统矩阵AΔ的特征值，从而判断系统的稳定性。当输出直流电压达到120 V 时为系统的平衡状态，以11 阶的小信号模型进行研究。为观察控制参数变化对系统稳定性的影响，使用控制变量法来进行分析。

令积分系数ki=0.1，将比例系数kp由5×10-8逐渐增加到3×10-6，AΔ矩阵的主导特征值的变化如图2（a）所示。当kp=5×10-8时，一对主导特征值处于右半平面，系统处于失稳状态，随着kp的增大，这对主导特征值向虚轴靠近，增大到5.4×10-8时穿过左半平面，系统变为稳定状态。当kp继续增大，这对特征值在远离虚轴的同时，另一对原来位于左半平面的特征值向虚轴靠拢，增大到2.68×10-6时穿过右半平面，系统变为不稳定状态。可见，过大或过小的比例系数均会使系统失去稳定，在本例中使系统稳定的比例系数区间为5.4×10-8～2.68×10-6。

令比例系数kp=1.5×10-6，将积分系数由0.1 逐渐增大到1.2，AΔ矩阵的主导特征值的变化如图2（b）所示。当ki=0.1 时，特征值均位于左半平面，系统处于稳定状态，随着ki的增大，一对特征值向虚轴靠近，增大到1.04 时穿向右半平面，系统处于不稳定状态。由此可见，积分系数过大会导致系统失去稳定，本例中使系统稳定的积分系数应小于1.04。

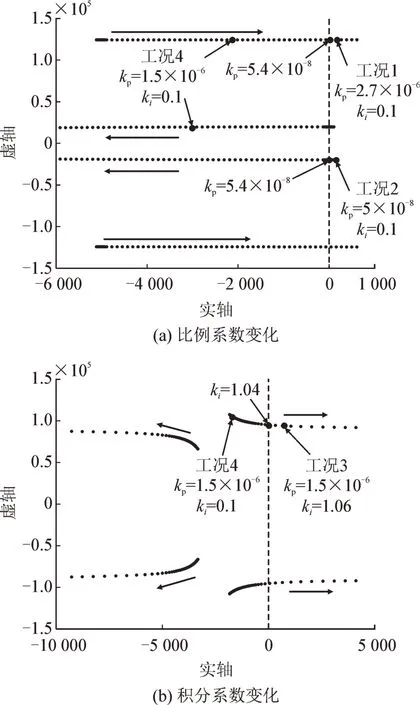
图2 控制参数改变时主导特征值的变化情况Fig.2 Variation of dominant eigenvalues with variation of control parameter

考虑工作情况及其稳定性判断见表2 所示的4种工作情况。根据图2 的特征值计算结果，工况1、2、3 有一组特征值位于右半平面，含实部为正的特征值，故可判断为不稳定情况；工况4 的特征值均位于左半平面，故可判断为稳定情况。

表2 考虑工作情况及其稳定性判断Table 2 Work conditions considered and its stability judgment

3.3 仿真验证

在Matlab/Simulink 中建立仿真模型，对以上所考虑工况的稳定情况进行验证。系统初始运行在工况4，在0.15 s 时分别将控制参数阶跃变化到工况1、2、3，不同工况对应的输出直流电压波形见图3。

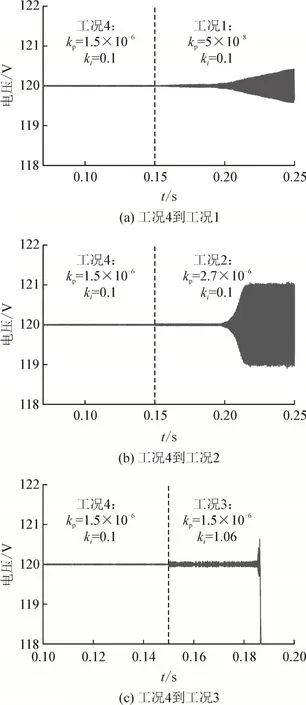
图3 工况变化时直流电压仿真波形Fig.3 Simulation waveform of DC voltage with condition variation

由图3 可知，系统初始时在工况4 时是能够稳定运行的，当分别阶跃到工况1、2、3 时，输出侧直流电压呈现不稳定状态，与表2 判断结果相符合。

4 结语

本文基于动态相量法，建立了考虑闭环控制器的SPS 控制策略下三相DAB 直流变换器小信号模型，所提模型能够正确分析系统的小信号稳定性，通过仿真验证得到以下结论：过大或过小的比例系数、过大和积分系数均会使系统失去稳定，要使系统稳定运行需将控制器参数限制在一定范围内。

本文利用动态相量对使用SPS 控制策略的三相DAB 直流变换器进行建模分析的方法，能够为使用其他控制策略的DAB 变换器小信号建模及稳定性分析提供新思路。

附录A

对于矩阵A中元素：

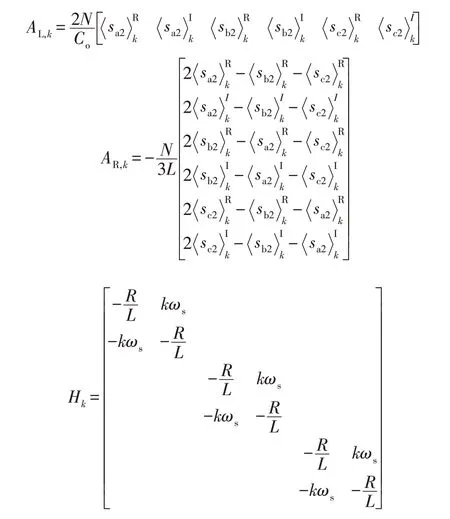
对于矩阵B中元素：

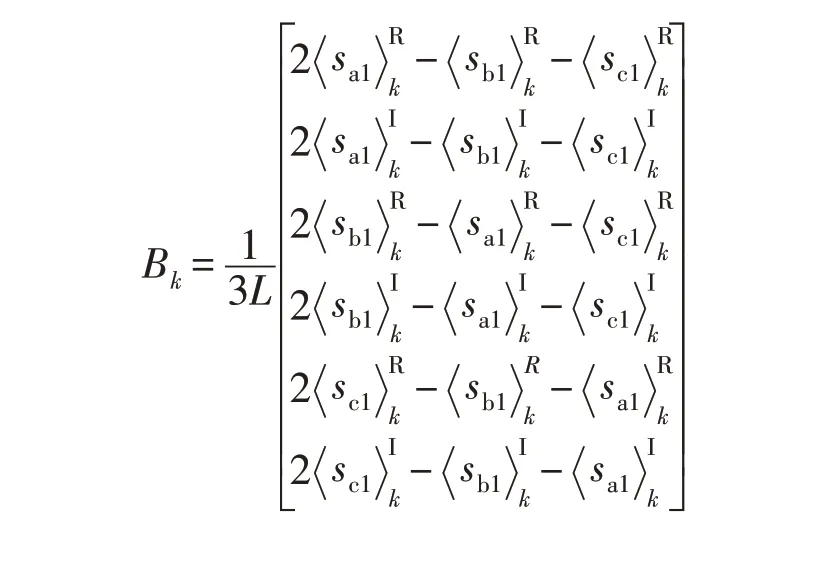
对于矩阵AΔ中元素：

对于矩阵BΔ中元素：