降低高电压风险的双馈风电机组低电压穿越参考功率整定

郑晗

（东北电力大学电气工程学院，吉林 吉林 132012）

0 引言

近年来，我国的风电联网技术快速发展，随着风电联网规模的不断增大，风电机组脱网事故对电网稳定性造成冲击[1-2]，机组脱网事故多由电网电压跌落引起，因此掌握风电机组在电网电压发生跌落故障时的LVRT 特性是保证电网安全稳定运行的重要前提。

针对于双馈感应发电机组（doubly fed induction generator，DFIG）的LVRT 过程，目前实践中广泛使用的LVRT 控制策略可以分成两类，一类是传统LVRT 控制策略[3-5]，另一类是改进的LVRT 控制策略[6-13]。传统LVRT 控制策略在电网电压发生跌落故障期间，Crowbar 保护回路会一直保持动作状态，DFIG 将会一直处于鼠笼异步电机的状态：此时DFIG 会从电网开始吸收无功功率，造成系统内无功功率冗余，机端电压无法迅速恢复正常，同时机端电压超出正常范围后，由于定子侧与电网直接相连，由于定、转子磁链的耦合作用，当定子磁链发生变化就会造成转子感应磁链产生变化，就会引起转子过电流问题，甚至损害转子变流器；另一方面电磁转矩发生振荡，可能引起DFIG 转子转速增大，甚至可能会发生DFIG 超速脱网事故[14]。

为了弥补传统LVRT 控制策略存在的不足，国内外提出了不同类型的改进LVRT 控制策略。文献[6-8]通过推导转子暂态电流，实现了Crowbar 电路的实时切除，但是该方法未考虑系统无功功率冗余对DFIG 机端电压恢复的影响。文献[9]提出了一种模糊自抗扰控制策略，通过运用广义微分的方法跟踪系统的信号，同时采用非线性函数实时修改参数，最终得到整个系统的扰动量并进行补偿，但文中提到的模糊控制器的控制算法较复杂，使得工作效率较低，不利于大规模推广使用。文献[10-11]通过推导暂态过程DFIG 表达式，对传统的Crowbar 保护回路进行改进，并使用直流卸荷回路共同提高DFIG 的LVRT 能力，但是直流卸荷回路会影响DFIG 在LVRT 期间的输出性能，同时此策略也未考虑DFIG 输出无功功率对机端电压恢复的影响。文献[12]提出了一种短路电流计算方法，通过推导LVRT 前后转子电流表达式，得到了考虑LVRT 控制影响的DFIG 并网系统短路电流的计算方法，并未考虑无功功率对机端电压恢复的影响；文献[13]兼顾了DFIG 不发生超速脱网和向电网提供无功功率支持的目标下对有功功率和无功功率进行整定，此策略主要关注在LVRT 期间有功功率对于转子机械转速的影响，但该策略未考虑无功功率对机端电压恢复速率的影响，DFIG 输出的无功功率过大将造成风电系统内无功功率冗余，可能引起电网电压在恢复过程中抬升过高，不利于机端电压快速恢复且会造成转子侧过电流问题。因此，基于该策略，LVRT 过程中参考功率整定方法还需要进一步研究。

本文基于电压跌落故障期间DFIG 整定的有功功率和无功功率之间的关系，提出了一种新型LVRT期间DFIG 参考功率的整定方法，在降低DFIG 发生超速脱网的风险时，同时满足DFIG 机端电压快速恢复的要求下去整定无功功率。最后，仿真结果验证了本文所提参考功率整定方法的有效性和可行性。

1 DFIG数学模型

典型的双馈感应风力发电机组的结构见图1。

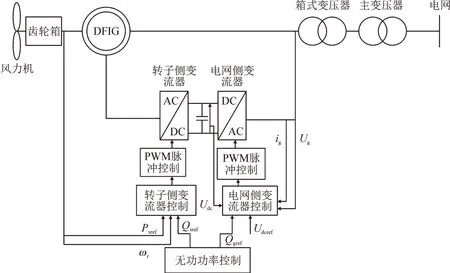
图1 典型双馈感应风电机组结构Fig.1 Structure of typical double-fed induction wind turbine

在dq 两相旋转坐标系中，本文采用发电机惯例，同时将变量折算至定子一侧，得到DFIG 的数学模型为

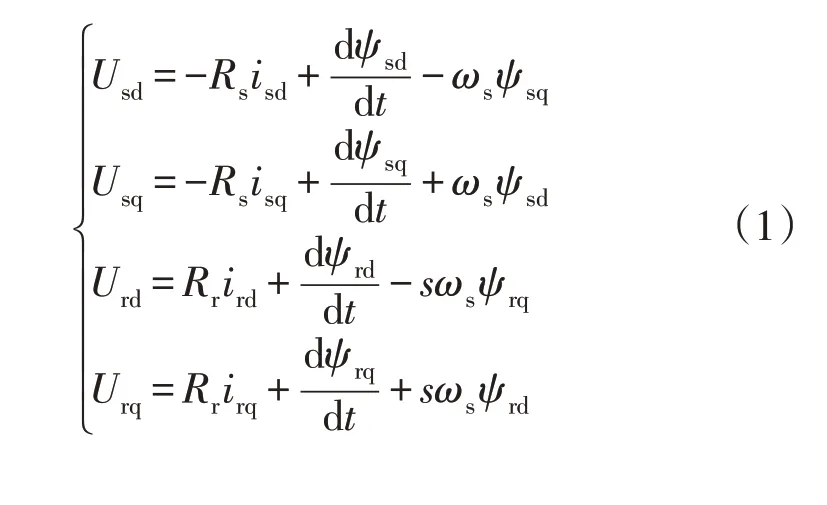
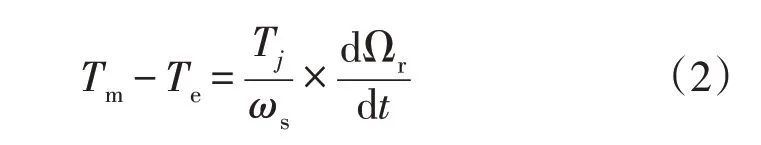
在式（1）中定、转子磁链的表达式为

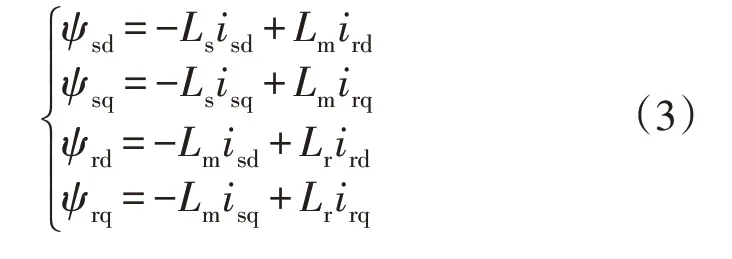
式中：Us为定子电压；Ur为转子电压；ψs为定子磁链；ψr为转子磁链；is为定子电流；ir为转子电流；下标量d、q为上述各量在两相旋转坐标系d、q轴下分量；Rs、Rr分别为定子和转子电阻；s为发电机转差；ws为定子角速度；Tm为机械转矩；Te为电磁转矩；Wr为转子机械角速度；Tj为惯性时间常数；Ls、Lr分别为定、转子电感的自感系数；Lm为定、转子电感的励磁电感系数。

基于上述数学模型的电压和磁链方程，采用定子磁链矢量控制，忽略定子电感大小，得到转子电流和定子电流的关系为

由此，定子侧输出的有功功率Ps和无功功率Qs分别为

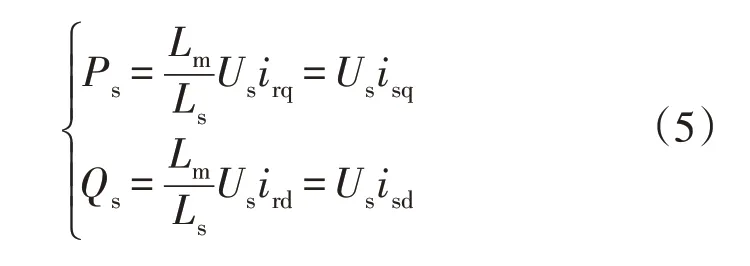
在正常运行的状态下，风电机组输出的有功功率大小根据最优功率Pbest与转子机械角速度Wr可得到最优功率为

2 DFIG低电压穿越方案

2.1 系统无功功率冗余风险分析

实际情况下，风电机组的并网运行具有一定共性规律，在因电网短路故障引起的多次风电机组脱网故障期间，系统电压均呈现先“低电压后高电压”的特点[15-20]。在电网发生短路故障之后，具备LVRT能力的风电机组将会进入LVRT 过程，为使得系统电压尽快恢复，风电机组会发出无功功率，由于风电机组自身无功调节速率较慢，使得系统内的容性无功功率冗余，机端电压继续迅速升高，导致风电机组无法快速恢复到正常电压范围。当机端电压升高，直至超出正常电压范围，与电网直接相连的定子磁链感应到电压升高的变化，由于定、转子磁链的耦合作用，当定子磁链发生变化就会造成转子感应磁链产生变化，转子磁链的动态变化就会引发转子过电流现象，甚至引起变流器内部器件击穿[21]。

2.2 双馈感应风电机组低电压穿越方案

基于前文分析，本文采取的LVRT 方案如下：

1）当电网电压发生跌落时，转子电流骤增至Crowbar 保护回路动作阈值时，Crowbar 保护回路投入保护，锁闭转子变流器脉冲信号，DFIG 将会进入LVRT 过程。

2）在电网电压跌落稳定期间，当转子电流的值衰减至Crowbar 回路退出阈值以下并持续20 ms时，切除Crowbar 保护回路并采用本文的参考功率整定方法。

3）当电网电压0.9U1≤Ug≤1.1U1（U1为电网相电压额定值）时，认定电网电压恢复正常状态，DFIG恢复正常运行状态[22]。

3 低电压穿越方案低电压穿越过程中参考功率整定方法

在电网电压跌落稳定期间，有功功率和无功功率的整定需要考虑以下方面：

1）有功功率方面：对于DFIG 而言，在电网电压跌落持续期间，DFIG 应该尽可能地输出有功功率，从而使得发生振荡的电磁转矩增大从而与机械转矩保持平衡关系，从而降低DFIG 超速脱网的风险。

2）无功功率方面：对于DFIG 而言，在电网电压跌落稳定期间，DFIG 需输出适量无功功率，使得机端电压在故障后能够快速恢复同时可以避免转子再次过电流问题。

基于以上分析，需要在兼顾降低DFIG 超速脱网风险和加速机端电压恢复，防止转子发生过电流这两个目标，对DFIG 输出的有功功率和无功功率进行整定[23]。

3.1 有功功率整定方法

假设当t=0 时，电网的电压发生跌落，Crowbar保护回路切入；转子电流衰减至满足Crowbar 回路退出条件时，Crowbar 保护回路退出；当t=625 ms 时刻，电压恢复正常。由文献[5]递推过程可得公式为

式中：Tm为DFIG 初始机械转矩，其值可根据DFIG正常运行时的初始工况得到；Tj和Ωrlim分别为惯性时间常数和转子极限转速，其值可查阅DFIG 技术参数得到；Ωr(0)为转子初始转速，可以测量得到。

式（7）即为DFIG 不发生超速脱网的有功功率的最小值整定公式。

3.2 无功功率整定方法

假设电网电压在故障跌落持续期间由U1跌落到U2，电网电压跌落故障结束后，DFIG 进行无功功率补偿，电网电压上升至U×2，为确保电网电压恢复后，DFIG 不超出正常电压范围，则需要满足以下关系（U1、U2均以标幺值表示），公式为

根据电力线路运行状况计算公式[10]为

式中：P、Q分别为LVRT 期间DFIG 发出的有功功率和无功功率；R、X分别为DFIG 的集电线路电阻和电抗；ΔU为电压低电压穿越故障后电网电压的抬升程度；U为电网电压低电压穿越故障后的电网电压，以上均为标幺值。

将式（8）、式（10）代入式（9）中，可得

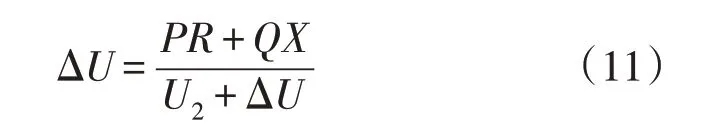
式（11）经推导可得

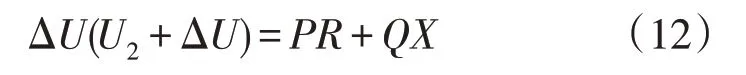
式（12）经过进一步整理后，可得一个关于ΔU的一元二次方程为

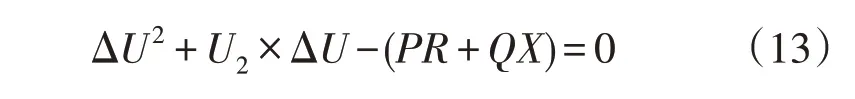
由一元二次方程的求根公式可以得到式（13）的两个根分别为

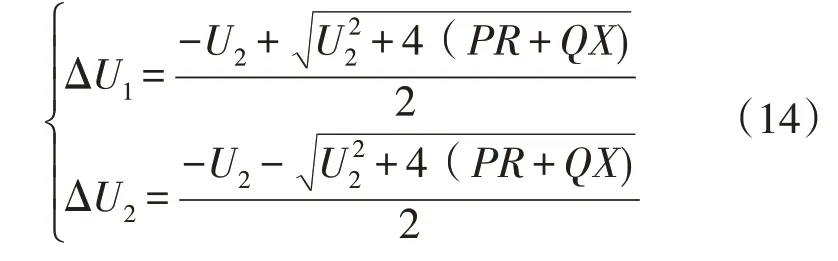
其中ΔU表示电压低电压穿越故障后电网电压的抬升程度，则ΔU＞0，因此可以得到ΔU的表达式为

其中ΔU、U2、R、X均为已知条件，Pmin由DFIG的初始工况决定，由式（12）得到DFIG 不发生超速脱网的Pmin，即可得到加速机端电压恢复的无功功率Qmax。

综上分析，DFIG 转子侧变流器的控制[24-26]框见图2。

图2 DFIG 转子侧变流器控制框图Fig.2 Control block diagram of converter at the side of DFIG rotor

4 仿真分析

为了验证本文提出的低电压穿越过程功率整定方法的有效性，下文进行了仿真分析。

4.1 仿真模型参数

本文在PSCAD/EMTDC V4.2.0 中搭建了某型号1.5 MW 的双馈感应风电机组，该型号DFIG 参数如下：额定功率为1.5 MW；额定电压为0.69 kV，转子机械角速度极限值Wrlim为1 900 rpm=1.233 p.u.，撬棒保护回路阻值为0.6 p.u.。转子侧额定电流为426 A，撬棒保护回路动作阈值为426×1.9=802.4 A，撬棒保护回路退出阈值为426×1.7=724.2 A，定转子匝数比为0.355，极对数p设置值为2，本文仿真模型模拟恒定风速为13 m/s，转子机械角速度初始值为1 750 rpm=1.16 p.u.，机械转矩为Tm=0.857，此时风力机发出的最优功率为1 286.06 kW，惯性时间常数Tj为5。线路电阻为0.17 p.u.，线路电抗为0.365 p.u.。其余DFIG 参数为：定子绕组为2.4 mΩ，转子绕组为2.2 mΩ，定子自感系数为1.978 mH，转子自感系数为1.947 mH，定、转子互感系数为1.858 mH。

4.2 运用本文参考功率整定方法仿真分析

本文参考功率整定方法仿真结果见图3。本文设定当t=0.5 s 前，DFIG 处于稳定状态，此时PS=Te=0.857 p.u.，QS=0，Ωr（0）=1 750 rpm。

图3 运用本文参考功率整定方法的仿真结果Fig.3 Simulation results by using the reference power setting methodin this paper

当t=1 s 时（对应仿真时刻为t=0.5 s）电网发生三相对称短路故障，电压U1跌落至0.5 p.u.，此时转子电流增大，当转子电流值超过Crowbar 保护回路动作阈值时，Crowbar 保护回路投入保护，转子侧变流器被锁闭，脉冲封锁。机械转矩Tm值基本不变，电磁转矩Te发生振荡，先增大然后降低，由于Tm和Te不相等，转子转速Wr一直增大。

当t=1.021 s 时（对应仿真时刻为t=0.521 s），转子电流大小达到Crowbar 回路退出条件，转子侧变流器重新投入，脉冲恢复，此时DFIG 采用本文提出的参考功率优化整定方法，可得Psref=Psmin=0.237 p.u.，Qsref=0.473 p.u.。

此后电压在跌落过程中达到稳态，U1=0.5 p.u.。Psref=Psmin=0.15 p.u.，Qsref=0.4 p.u.。由于Tm和Te仍不相等，转子转速Ωr继续增大。

当t=1.625 s（对应仿真时刻为t=1.125 s），电压U1故障切除，电压恢复却引起了转子电流的再次增大，当t=1.632 s（对应仿真时刻为t=1.132 s），Crowbar 保护回路再次动作，锁闭转子侧变流器的脉冲，此时Tm和Te仍不相等，因此转子转速Ωr继续增大。

当t=1.653 s（对应仿真时刻为t=1.153 s）时，转子电流大小衰减后达到Crowbar 保护回路退出要求，转子侧变流器重新恢复控制。DFIG 恢复正常运行模式。此时Ps=Te=0.857 p.u.，Qs=0 p.u.。但是Crowbar 保护回路的退出引起电磁转矩震荡，因此转子转速Ωr继续增大。

当t=1.655 s 时（对应仿真时刻为t=1.155 s）恢复正常，定子相电压U1=1.0 p.u.。

当t=1.659 s（对应仿真时刻为t=1.159 s）时，转子转速Ωr达到整个过程的最大值，Ωr（1.159）=1 898 rpm＜Ωrlim，此后转子转速开始减小，逐步恢复正常。

4.3 验证本文无功功率整定方法仿真分析

为验证本文所提出的无功功率整定方法有效性。设置如下对比分析[24-26]：本文设定在LVRT 期间，Qsref=0.453 p.u.。由于DFIG 自身无功功率调节较慢，在电压故障切除100 ms 内仍发出无功功率，此后DFIG 恢复正常，仿真结果见图4。

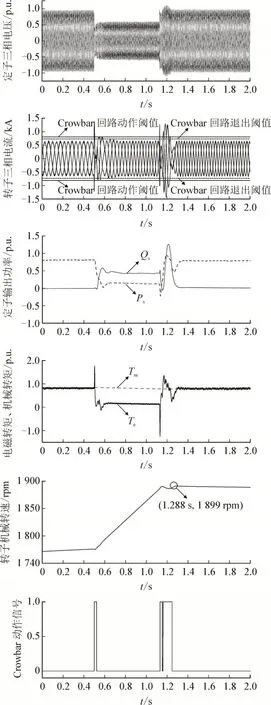
图4 验证本文无功功率整定方法的仿真结果Fig.4 Simulation results for verifying reactive power setting method in this paper

在当t=1.021 s 时（对应仿真时刻为t=0.521 s）时，此时转子侧变流器重新投入运行，脉冲恢复，在跌落电压达到稳态的过程中[27-29]，Qsref=0.533 p.u.，Psref=0.09 p.u.。在跌落电压达到稳态后，Qsref=0.453 p.u.，Psref=0.13 p.u.。在t=1.625s 时（对应仿真时刻为t=1.125 s），电压U1故障切除，机端电压开始恢复正常。当t=1.632 s 时（对应仿真时刻为t=1.132 s），Crowbar 保护回路再次动作，于t=1.653 s 时（对应仿真时刻为t=1.153 s）退出保护。由于DFIG 自身无功功率调节速率较慢，导致DFIG 会继续发出无功功率，机端电压继续上升，当t=1.661 s 时（对应仿真时刻为t=1.161 s），转子电流再次增大超出Crowbar动作阈值，引发Crowbar 保护回路再次动作。当t=1.701 s 时（对应仿真时刻为t=1.201 s），定子相电压达到了最大值U1=1.2 p.u.。此后Qsref恢复为0，当t=1.735 s 时（对应仿真时刻为t=1.235 s），定子相电压U1=1.0 p.u.恢复正常。当t=1.750 s 时（对应仿真时刻为t=1.250 s），Crowbar 退出保护。

综上通过对比分析，运用本文参考功率整定方法，DFIG 在降低自身超速脱网风险的同时，向电网提供适量的无功功率支持从而在完成LVRT 过程后机端电压能够恢复，且转子侧未发生过电流问题[30-33]。

5 结语

本文在防止DFIG 发生超速脱网的有功功率整定方法的基础上提出了一种加速机端电压恢复、防止转子发生过电流的无功功率整定方法，仿真分析结论如下：

电网电压跌落持续期间，由降低DFIG 超速脱网风险为目标得到的Pmin，整定对应电网电压抬升程度对应DFIG 的Qmax，在防止DFIG 发生超速脱网事故的同时，可使DFIG 向电网输出适量的无功功率来加快机端电压恢复速率，防止转子侧发生过电流事故，仿真结果验证了本文所提参考功率整定方法的有效性和可行性。