基于电压电平的MMC 直接功率预测控制策略

熊盛涛，刘振兴，廖雪超

（1.武汉城市学院，武汉 430081；2.武汉科技大学，武汉 430083）

0 引言

模块化多电平转换器（MMC）具有结构模块化、冗余控制、可以独立控制有功功率和无功功率等优点[1-5]，在中高压研究应用中得到了极大的发展，如高压直流（HVDC）输电、中压配电网、静态同步补偿器（STATCOM）等。MMC 控制器需要考虑多个控制目标，包括电容电压平衡控制，桥臂环流抑制控制，功率控制等，控制能力不足可能导致换流站损耗增加，甚至影响其稳定运行。因此，提高现有MMC 控制策略的性能具有重要意义。

目前已有大量文献开展了MMC 控制策略的研究。常见的控制策略有多载波脉宽调制（pulse width modulation，PWM）、特定次谐波消去PWM 策略等。随着研究的深入，有限控制集模型预测控制（finite control set model predictive control，FCS-MPC）受到了专家学者的关注。文献将FCS-MPC 用于MMC控制，其在每个控制周期内分别预测上下桥臂所有开关组合对应的交流电流、环流电流、子模块电容电压，选择最优开关组合作为下一周期输出[6-12]。但该方法随着桥臂子模块数目增加，开关状态组合数量也急剧增加，导致了较大的计算量。最常用的减少计算量的方法是基于电压电平的FCS-MPC 电流控制策略[13-15]。文献-采用上下桥臂输出电平数作为有限控制集合，通过评估电压电平的数量（而不是开关状态）实现成本函数的最小化。然而这种控制需要内部电流控制回路，并且需要旋转坐标变换，控制结构较为复杂。此外，这类策略由于直接控制电流，对于功率的调节控制存在局限性。

针对上述问题，本文提出了一种基于电压电平的MMC 直接功率预测控制（predictive direct power control，PDPC）策略。所提策略不需要锁相环采集角度信息，能够摆脱旋转变换和内环电流计算，并且采用三相统一控制，能简化控制结构。FCS-MPC 电流控制通过最小化电流控制误差来间接调节功率，而所提控制策略通过最小化有功和无功功率控制误差直接调节功率，因此所提策略在降低功率纹波和功率追踪方面具有显著优势，最后通过仿真验证了所提策略的有效性。

1 MMC数学模型

三相MMC 的拓扑结构见图1。每相的上桥臂、下桥臂均由N个子模块（SM）串联组成，每个SM 由1 个直流电容器和2 个IGBT 组成。正常工作时SM 有2 种运行模式，即关断模式和导通模式，SM 处于关断模式时，输出电压为零，SM 处于导通状态时，其输出电压等于电容器电压vc，导通模式下，电容器根据电流方向充电或放电。与上臂相关的参数用下标u 表示，与下臂相关的参数用下标l表示。

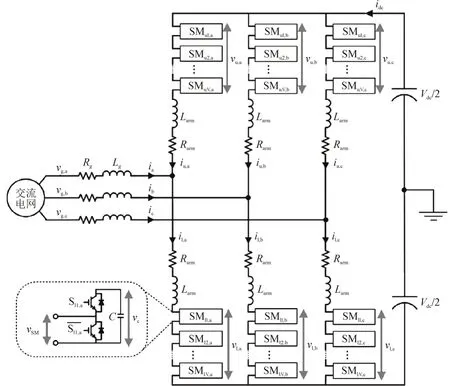
图1 MMC拓扑结构示意图Fig.1 Schematic diagram of MMC topology

基于基尔霍夫电压定律，可得到MMC 在j相的动态响应方程为

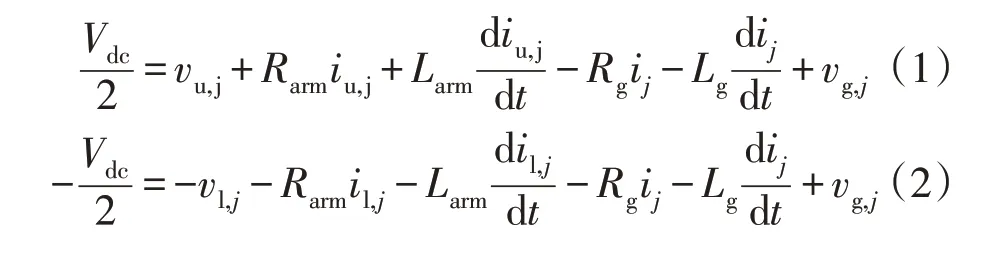
式中：Vdc为直流侧电压；vg,j为网侧电压；vu,j，vl,j分别为上桥臂电压和下桥臂电压；Rarm和Larm分别为桥臂电阻和电感；Rg和Lg分别为网侧电阻和电感。其中相电流ij、j相上下臂电流iu,j、il,j的关系式可以表示为

式中：idc为直流侧电流；iz,j为j相环流。

由式（3）和式（4）可得j相环流表达式为

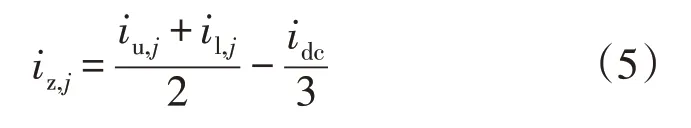
通过式（1）、（2）推导相电流和桥臂环流的动态方程为

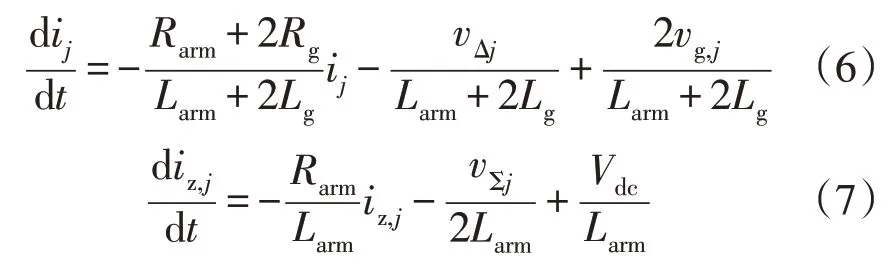
式中vΣj为上下桥臂电压之和；vΔj为上下桥臂电压之差。其定义为

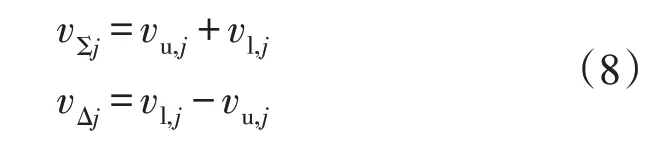
j相的桥臂电压表示为

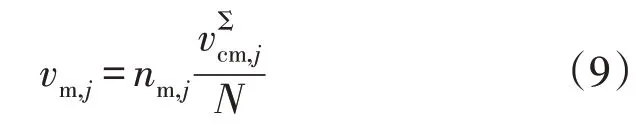
式中：nm,j为导通的子模块数量；vΣcm,j为所有子模块电容电压的总和，下标m∈{u,l}。将等式（9）代入等式（8），可得

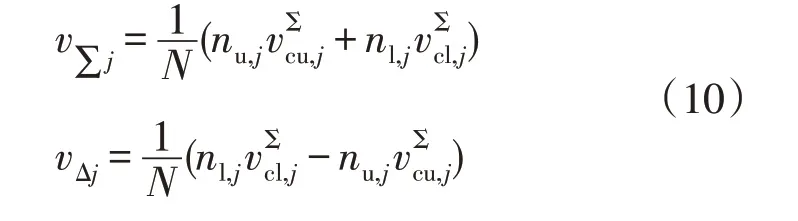
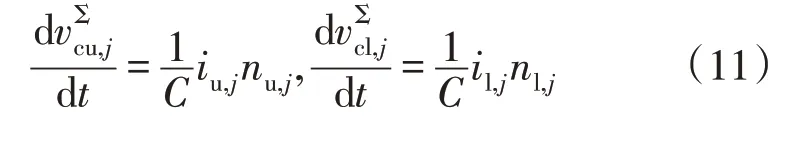
2 基于电压电平的直接预测功率控制设计

网侧电压vj经clark 变换可得

基于瞬时功率理论，有功功率P和无功功率Q可表示为

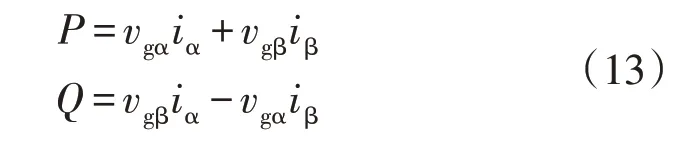
由式（13）可得有功功率和无功功率的时间导数为

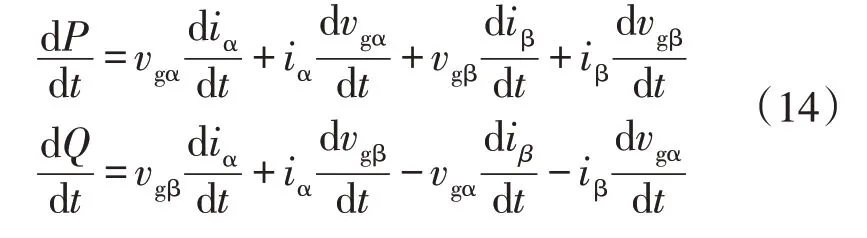
将相电流和网侧电压的时间导数代入式（14），即可得到表达式。

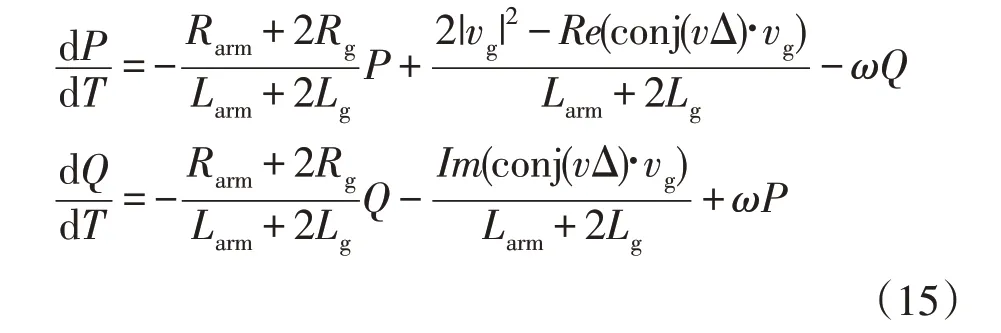
对式（7）和式（15）分别进行离散化处理，可获得式（16）-（18）。

所提PDPC 策略的控制目标共有3 个：第1 个控制目标是最大限度地减少参考功率和实际功率间的误差，以确保精准的功率跟踪；第2 个控制目标是消除或最小化桥臂环流，以减少子模块电容电压波动；第3 个控制目标是使子模块电容电压和电压参考值的偏差最小。总体目标函数根据3 个控制目标及其相应的权重因子可以表示为

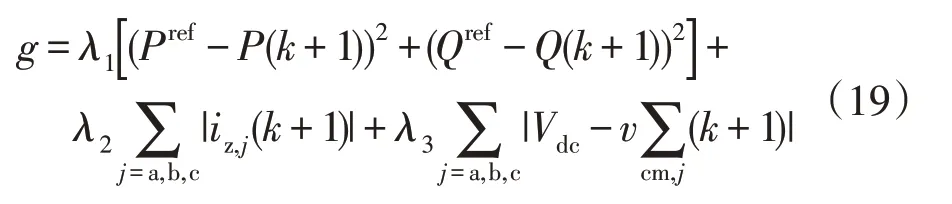
增加权重因子λ1、λ2和λ3将分别增加对电能质量、桥臂环流和电容电压的重视程度。

所提PDPC 策略控制框图，如图2（a）所示。基于瞬时功率理论，由网侧电压和电流计算第k时刻的有功功率和无功功率，分别利用等式（16）-（18）中的离散预测模型计算下一时刻的预测功率、桥臂电流和SM 电容电压总和。然后对每个可能的电压电平评估等式（19）中定义的目标函数，直到选择了实现成本函数最小的最优电压水平。然后将最优的nu,j和nl,j代入排序算法，得到最优开关状态。

基于电压电平的预测电流控制框图，如图2（b）。该控制的一个重要特征是，他需要一个锁相环（phase locked loop，PLL）测量电网电压的相位角θ，以便根据所需的功率参考值计算相电流参考值。而所提控制通过在αβ 参考坐标系中表示向量，因此不需要PLL进行锁相。另外，在基于电压水平的电流控制中，各相控制之间相互独立，需要逐相控制。所提PDPC 策略采用三相统一控制，可以更好地调节功率和电流。

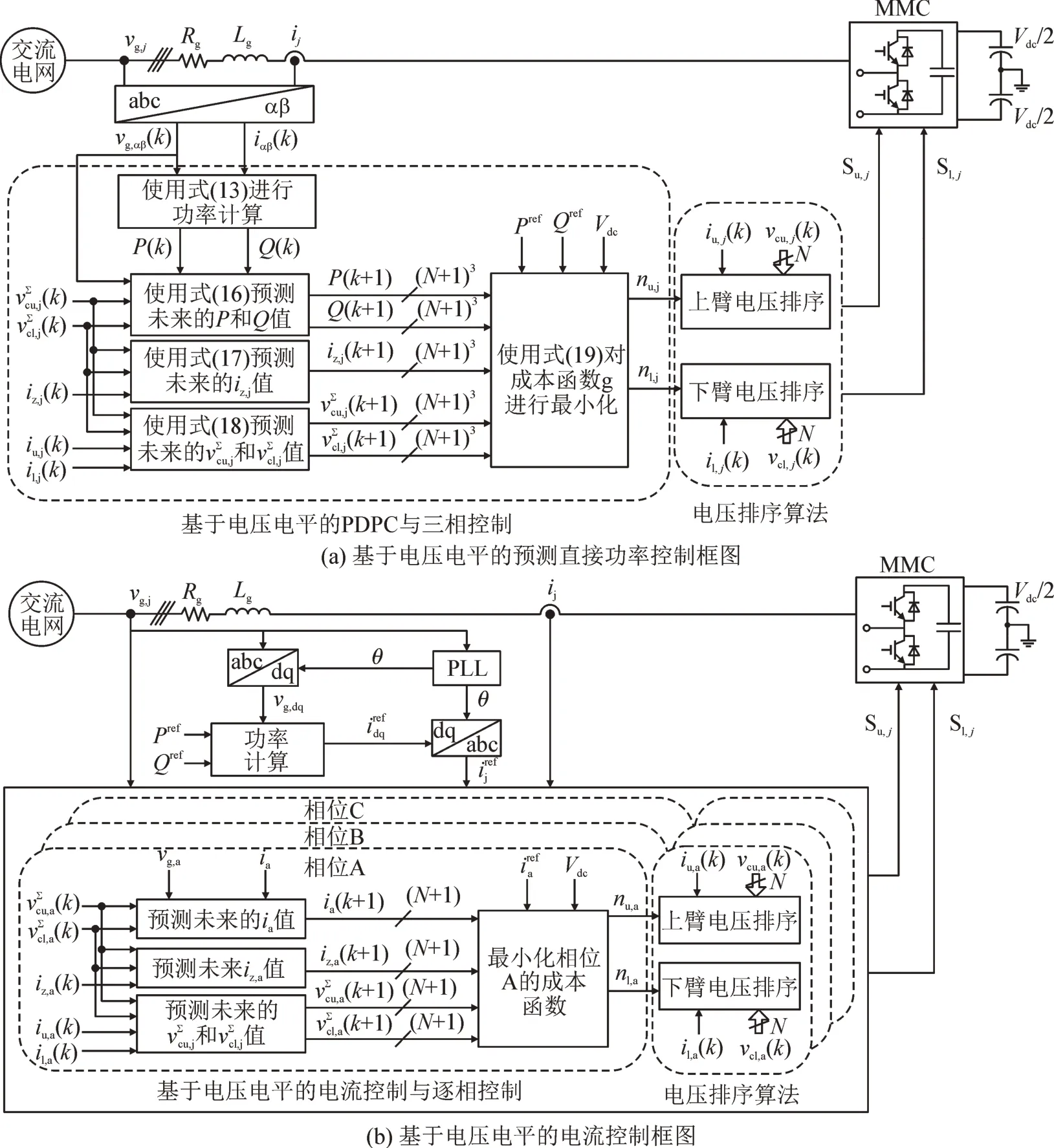
图2 控制框图Fig.2 Control block diagrams

3 仿真分析

为验证所提控制策略的可行性，在Matlab/Simulink 环境中进行了仿真验证。将所提PDPC 策略与一种典型的基于电压电平的预测电流控制进行比较，为后文描述方便，将其简称为预测电流控制。由于所提的PDPC 策略将导通的SM 总数限制为N，为保证比较的可靠性，在预测电流控制中采用相同的数目。表1 列出了2 种控制方法的相关系统参数。

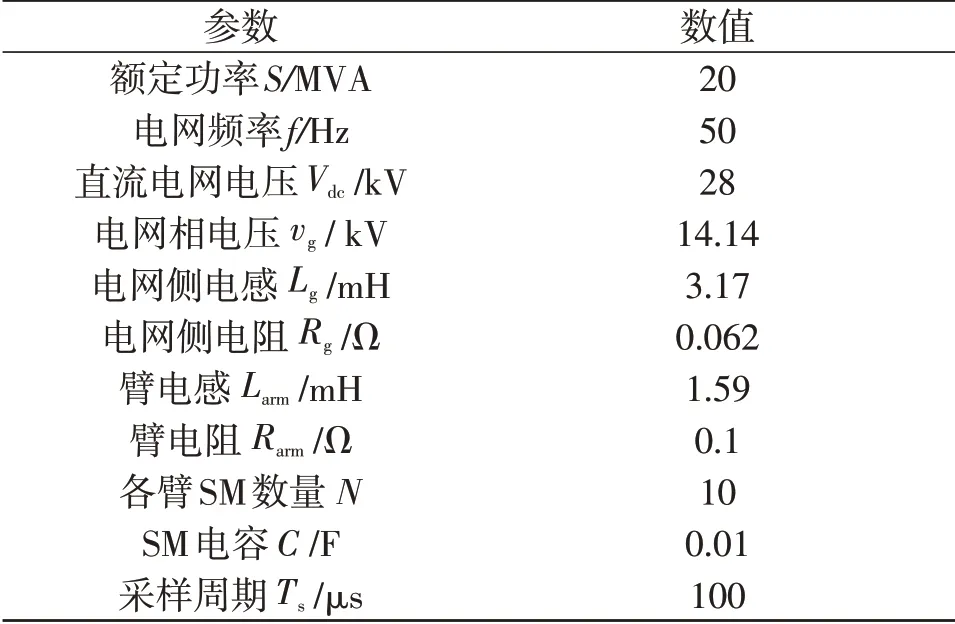
表1 系统参数Table 1 System parameters

3.1 暂态特性结果分析

图3 为功率参考值变化时预测电流控制和所提控制策略的暂态特性。初始时，瞬时有功功率和无功功率都保持为零。然后，有功功率参考值在0.1 s 后从0 上升到10 MW，而无功功率参考值在0.2 s 之后从0 下降到-10 Mvar。由图可知，两种控制策略中的上升时间和下降时间几乎是相同的。这意味着所提控制策略保留了预测电流控制固有的快速响应特性。

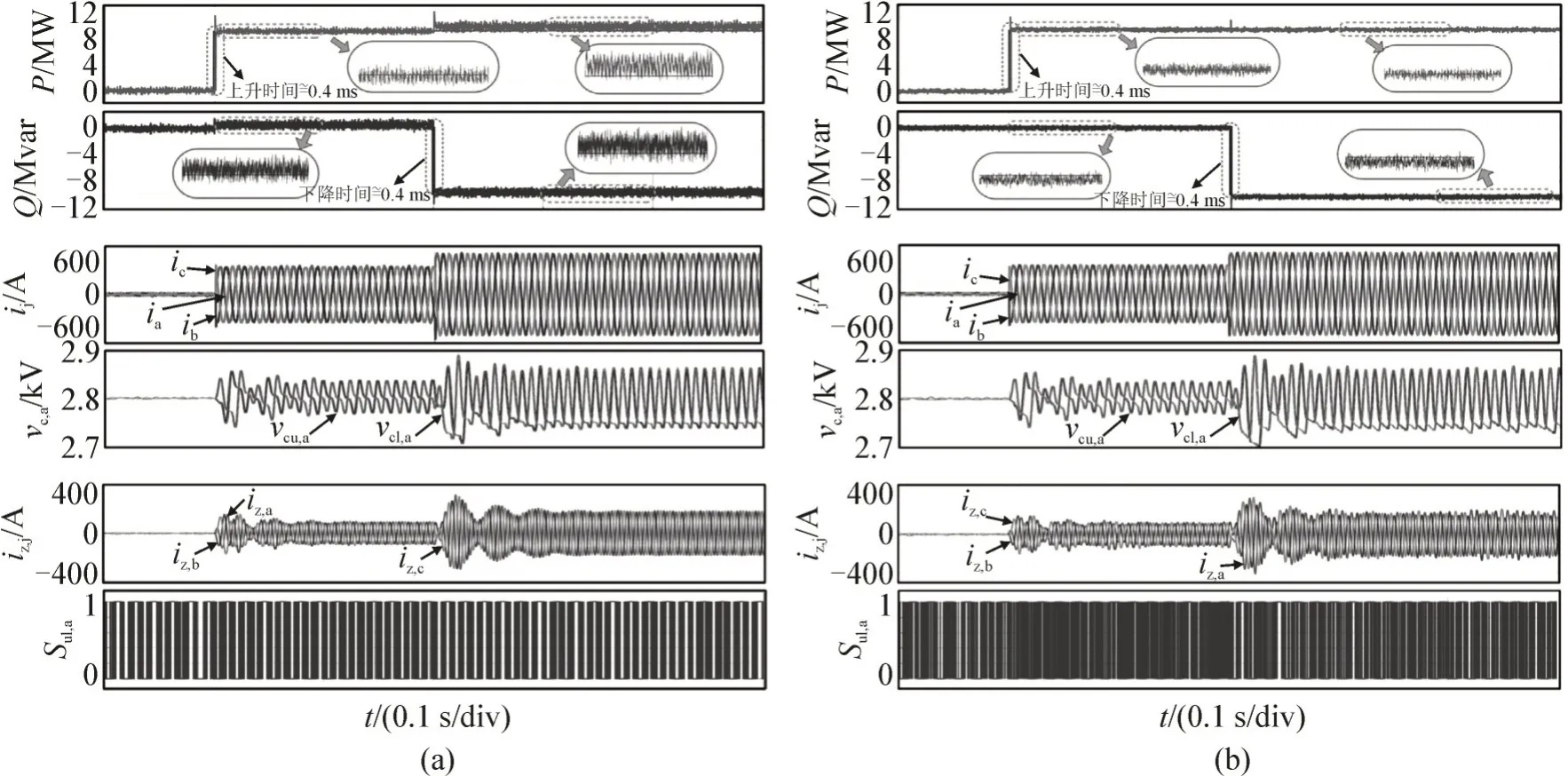
图3 功率阶跃的暂态响应Fig.3 Transient response of power step

在功率追踪特性方面，预测电流控制存在功率跟踪不准确的缺点。当Pref上升至10 MW 时，无功功率无法跟踪其参考值，而当Qref下降为-10 Mvar 时，有功功率则偏离其参考值。相比之下，所提控制策略可以保证全时段对参考值进行准确的功率跟踪。此外，预测电流控制的功率波动更为明显。

仿真结果还表明，这两种控制方法对电容电压波动和桥臂环流具有近似的控制能力。

图4 为网侧发生单相接地故障时预测电流控制和所提控制策略的暂态特性。其中，Pref定为10 MW，Qref定为0。0.2 s 时刻网侧发生A 相单相接地故障，故障时间设置为0.2 s。在两种控制方法中，有功功率和无功功率纹波都有所增加。此外，两种控制均能很好地调节SM 电容电压至其标称值。然而，在故障期间，所提策略的SM 电容电压波形更小。故障期间两种策略对相电流和循环电流的控制特性较为相近。

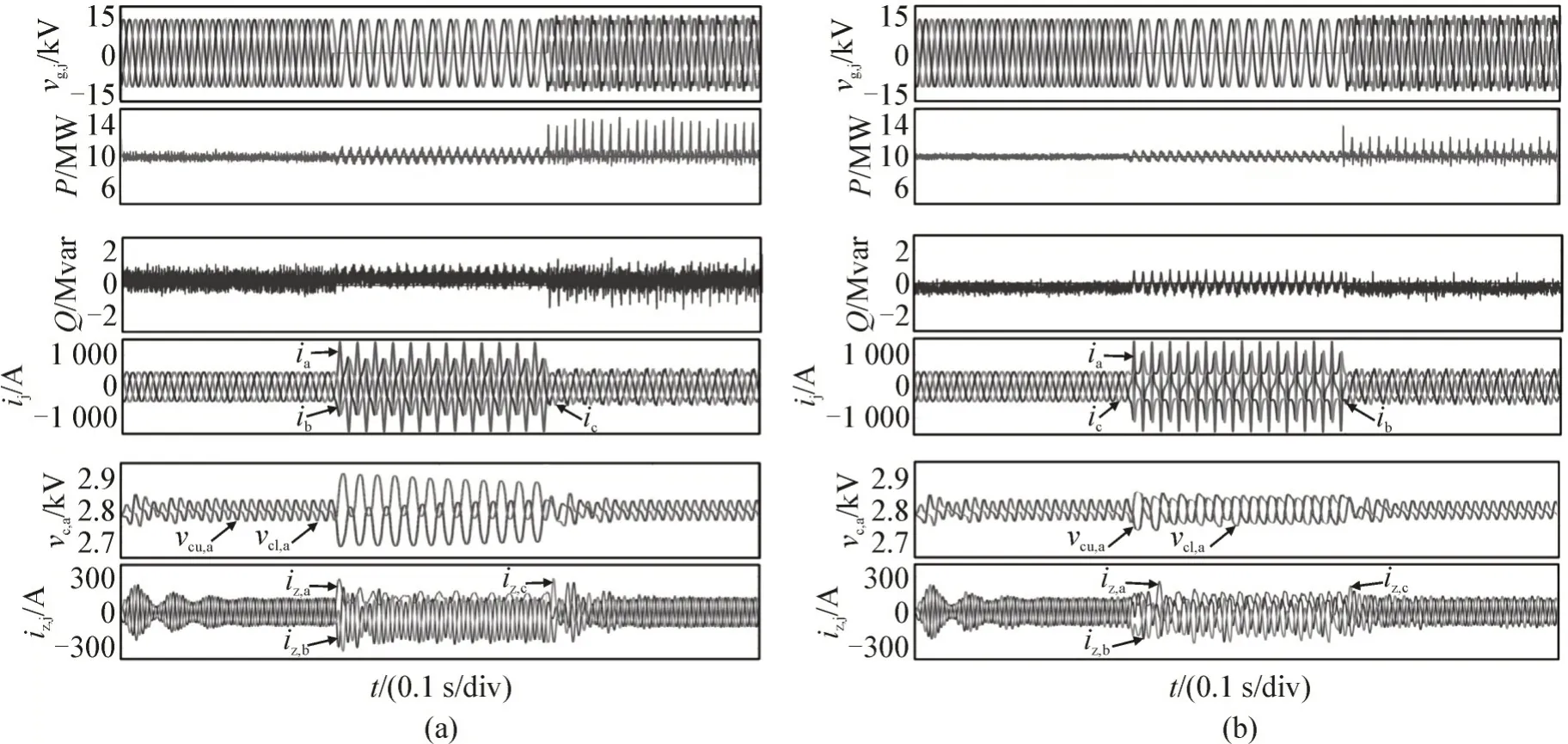
图4 网侧单相接地故障的暂态响应Fig.4 Transient response of single phase to ground fault at grid side

3.2 稳态特性结果分析

为了进一步验证所提控制策略的效果，考虑在不同工况下对两种控制技术的系统特性进行研究。本文选取3 个重要指标来衡量控制效果，即平均环流纹波，平均电容电压纹波(vc_ripple)，和平均功率误差。平均环流纹波定义为

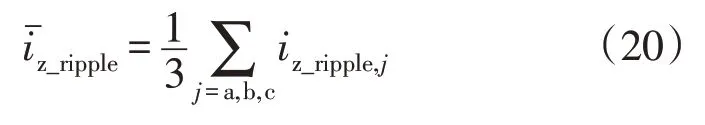
通过对各子模块的vc纹波求平均，可得平均电容电压纹波。

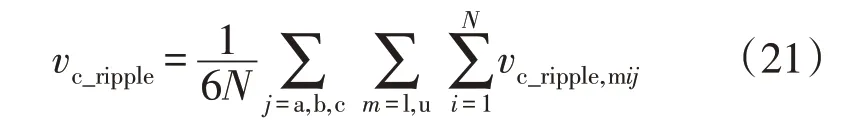
在时间间隔Tc内，对有功功率和无功功率的平均功率误差可表示为

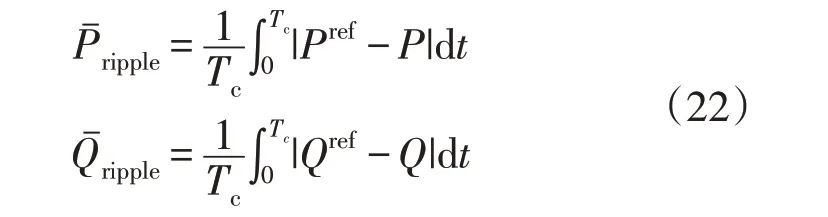
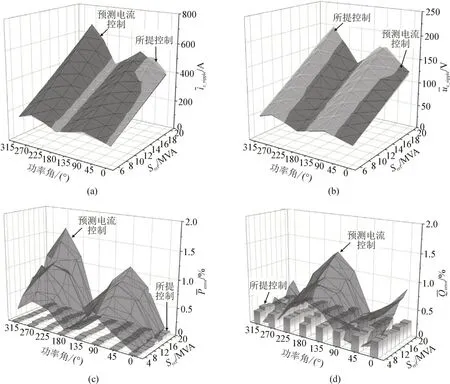
图5 各工况下的稳态特性Fig.5 Steady state characteristics under various working conditions

3.3 针对网侧电感失配的鲁棒性分析

预测电流控制和所提控制策略中都包含了电网参数信息。如果模型中使用的参数与实际值完全相同，则两种算法都可以正常工作[16-19]。但实际中存在着参数失配现象，会影响基于预测控制的精度。因此，本节专门研究所提控制策略在电网参数失配时的鲁棒性。由于网侧电阻失配对换流器性能的影响可以忽略不计，因此仅考虑网侧电感失配。网侧电感的失配定义为ΔLg，并表示为

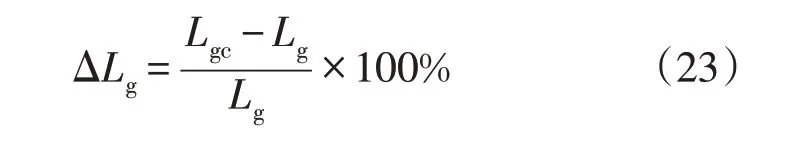
式中：Lg为实际电感值；Lgc为用于控制的电感值。

需要注意的是，ΔLg为负值，意味着预测算法低估了网侧电感(Lgc＜Lg)；而ΔLg为正值，则意味着预测算法高估了网侧电感(Lgc＞Lg)。

设定Pref为20 MW，Qref为0。图6 为当网侧电感失配为±50% 时，两种控制策略的功率响应特性。在ΔLg=-50%的情况下，预测电流控制中的功率纹波显著增加，并且无功明显偏离参考值。所提策略的有功功率纹波会略有增加。但是，几乎没有观察到功率误差。此外，在两种控制策略中，高估的Lgc(ΔLg=50%)对功率特性的影响并不显著。

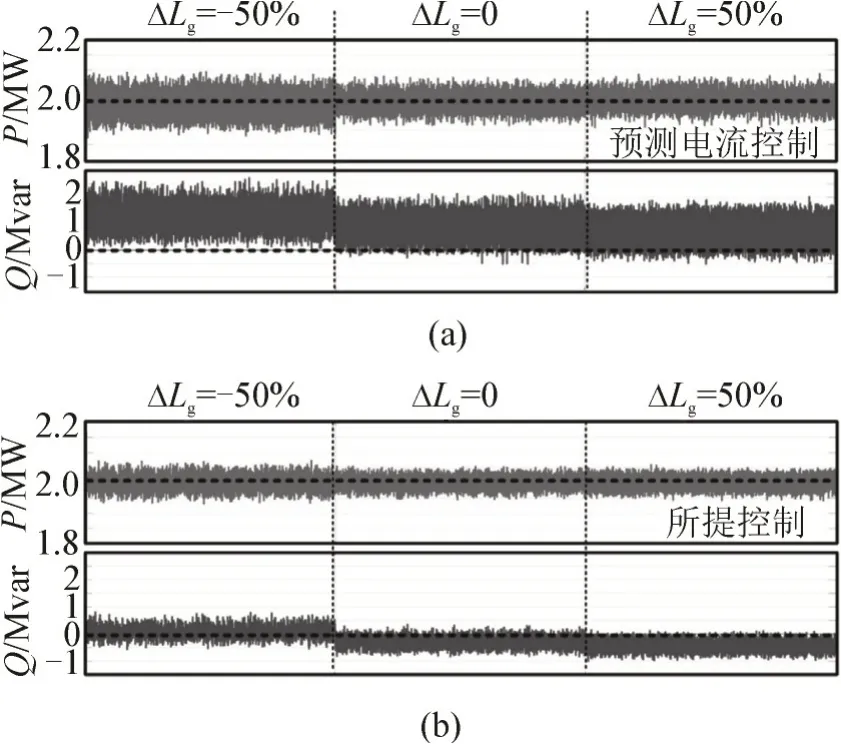
图6 网侧电感失配时的功率响应特性Fig.6 Power response characteristics in inductance mismatch of grid side

此外，为了分析ΔLg对于电容电压和桥臂电流的影响，图7 给出了在网侧电感失配时，vc_ripple和的变化情况。

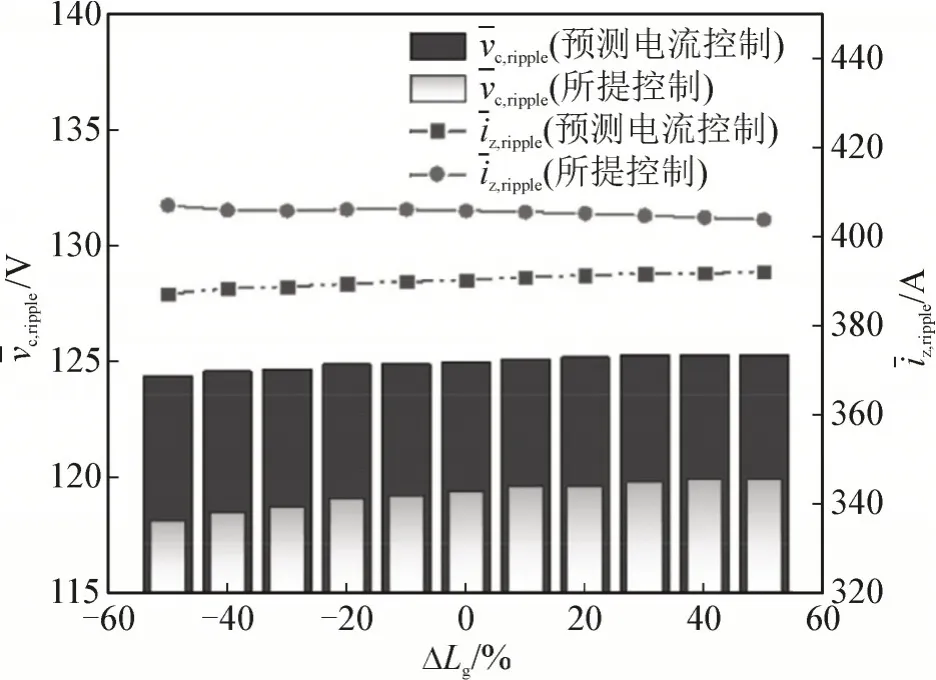
图7 网侧电感失配对电容电压和桥臂电流的影响Fig.7 Influence of inductance mismatch of grid side on capacitor voltage and bridge arm current

由图可知，vc_ripple和几乎不受ΔLg影响。此外，两种控制策略中的vc_ripple都随着ΔLg正向增大而略有增加，而随着ΔLg负向增大而稍有下降。综上所述，在不同ΔLg的控制条件下，系统仍能保持稳定。所提控制策略在电感失配时，对于降低功率波动和功率追踪效果均优于预测电流控制。

4 结语

针对模块化多电平变流器（MMC）传统控制复杂的问题，本文提出了一种基于电压电平的模块化多电平换流器直接功率预测控制策略。首先建立了MMC 的数学模型，接着给出了所提控制策略的设计思路以及控制框图，最后仿真验证了所提策略的有效性。所得结论如下：

1）所提控制策略的控制结构相比于预测电流控制更为简单。该策略基于αβ 变换，无需PLL 提供角度信息。此外，该策略采用三相统一控制，而预测电流控制需要各相控制相互独立，需要逐项控制。

2）所提控制策略在稳态和暂态均能表现出优异的降低功率波动和功率追踪的能力。此外，所提控制策略能保持与预测电流控制相同的响应速度，对电容电压和桥臂电流的控制能力几乎相近。

3）所提控制策略在网侧电感参数失配时能有效控功率，具有鲁棒性。通过仿真结果可知，预测电流控制的平均功率误差受功率角的影响较大，而所提控制策略几乎不受影响。