一种降低MMC 换流器子模块电容体积的方法

阎国强，王威儒，朱博

（1.上海市公用事业学校，上海 200030；2.东北电力大学电气工程学院，吉林 吉林 132012；3.中国南方电网有限责任公司超高压输电公司广州局，广州 510000）

0 引言

模块化多电平换流器（modular multilevel converter，MMC）具有输出电压电流谐波分量小、损耗低、便于扩展等优点[1]，自2001年由德国学者提出这种拓扑结构后便受到了广泛的关注，各个科研机构及高校的学者对其换流站控制策略[2]、换流阀控制策略[3]、紧急功率支撑策略[4]等各个方向进行了大量的研究，使其成为高压大容量电压源换流器的主流发展方向，在高压直流输电方面具有广阔的应用前景。2010年美国建设了Trans Bay Cable 工程[5]，他是世界上首个基于MMC 的柔性直流输电工程，拉开了MMC 换流器投产运行的序幕。我国已经陆续建设了南汇双端风电消纳工程[6]，舟山五端风电外送工程[7]，厦门双端岛屿供电工程[8]，以及张北四端直流电网[9]等一系列的柔性直流输电工程。但目前各工程均采用大电容来降低子模块电容电压波动，导致换流阀塔巨大，不利于组装、拆卸与运输，同时降低了换流器的经济性。

针对上述问题，文献[10]提出了一种在不对称交流电网条件下的直流电压稳定控制策略，虽然有效地抑制了直流侧电压的波动，但并没有落实到各桥臂的子模块上，不能确定子模块电容电压波动量是否降低。文献[11]提出了一种基于空间矢量脉宽调制的方法来降低子模块电容电压波动量，但在实际工程中，子模块数量庞大，更倾向于采用最近电平逼近的调制策略。文献[12]提出了一种控制桥臂能量的方法来降低各个桥臂的能量波动，该方法可有效提升桥臂间子模块电容均压效果，但对子模块电容电压波动量抑制效果有限。

此外，在换流器桥臂注入谐波电流也是抑制子模块电容电压波动的重要策略，文献[13-14]提出了通过注入二次环流来降低子模块电容电压波动的方法，但注入二次环流会增加IGBT 的开关频率，增加换流器损耗，降低子模块的使用寿命。文献[15]针对低频工况下的MMC 换流器提出了注入方波共模电压分量的方法，对电容电压波动起到了一定的抑制效果，但零序分量会对交流侧和直流侧都产生不利的影响，在此基础上，文献[16]提出了基数次高频注入法，较传统方法引入了相对较少的高频环流，并且比方波注入法更易实现。

为进一步降低子模块电容电压波动，本文从换流器主电路拓扑的角度提出一种改进半桥子模块（half bridge sub-model，HBSM）和改进全桥子模块（full bridge sub-model，FBSM）相结合的方式来降低子模块电容电压波动量，使得子模块可以选取较低容值的电容，进而降低子模块体积。HBSM 与FBSM 混合构建的MMC 换流器目前已在南方电网公司昆柳龙直流工程的柳州和龙门换流站得到应用，用以提高换流站的主动故障抑制能力和故障穿越能力，以降低直流断路器和故障限流器的投入成本[17-19]，该方案具有一定的工程适用性。此外针对仿真中遇到的FBSM 电容电压波动较大的问题，提出了用本相HBSM 电容电压与后一相FBSM 电容电压进行互补的方法进行均压控制，以降低FBSM电容电压的波动。最后基于1 500 MW 的±250 kV柔性直流数字仿真系统进行对比仿真，结果表明采用本文提出的电容电压波动抑制方法可以使子模块电容值大幅度下降。

1 MMC桥臂能量波动分析

MMC 换流器拓扑结构见图1。

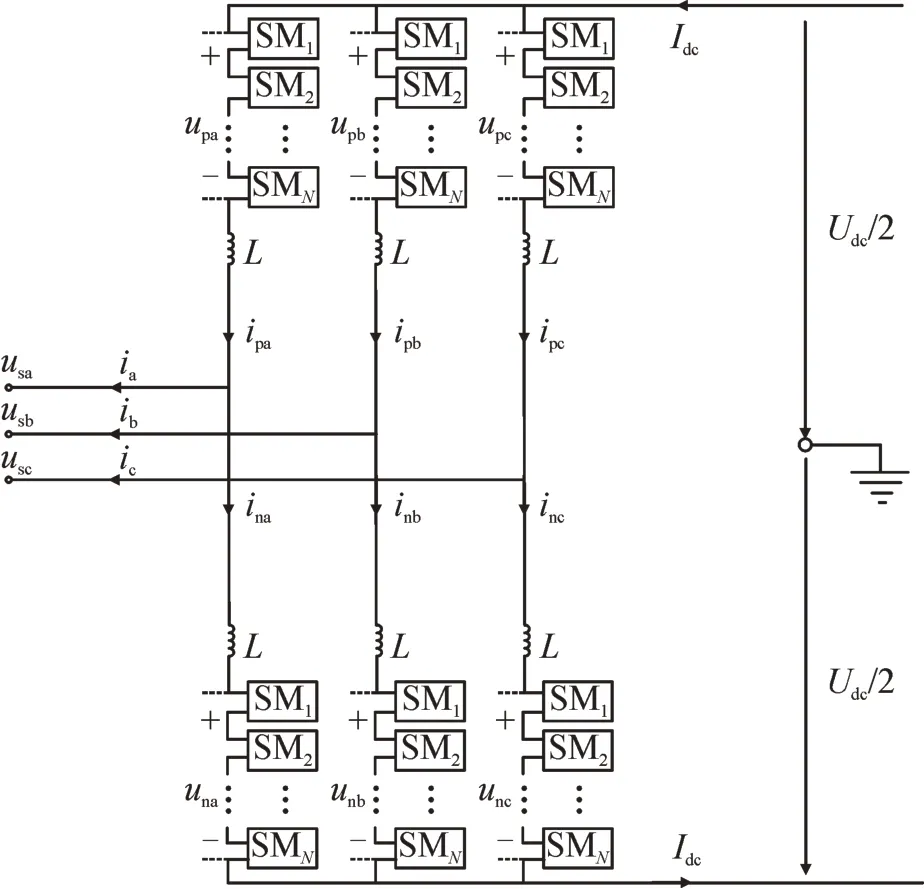
图1 MMC主电路拓扑结构图Fig.1 Topological diagram of main circuit of MMC

各相上、下桥臂均由N个子模块（sub-model，SM）、电感L串联而成，通过对子模块投入和切除的控制，实现对正弦交流电压的拟合。所以各个子模块可以等效成可控电压源[20]。

其中：ux和ix分别为交流侧的三相电压和电流（x∈[a，b，c]），ipx和inx分别为三相上、下桥臂电流，upx和unx分别为三相上、下桥臂电压，Udc和Idc分别为直流母线的电压和电流。环流抑制后，各桥臂电压电流满足关系公式为

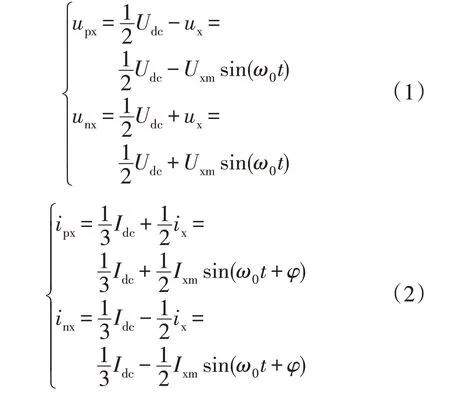
式中：Uxm和Ixm分别为各相交流电压电流峰值；ω0为角频率；φ为相位角。

可以求出各桥臂的瞬时功率为

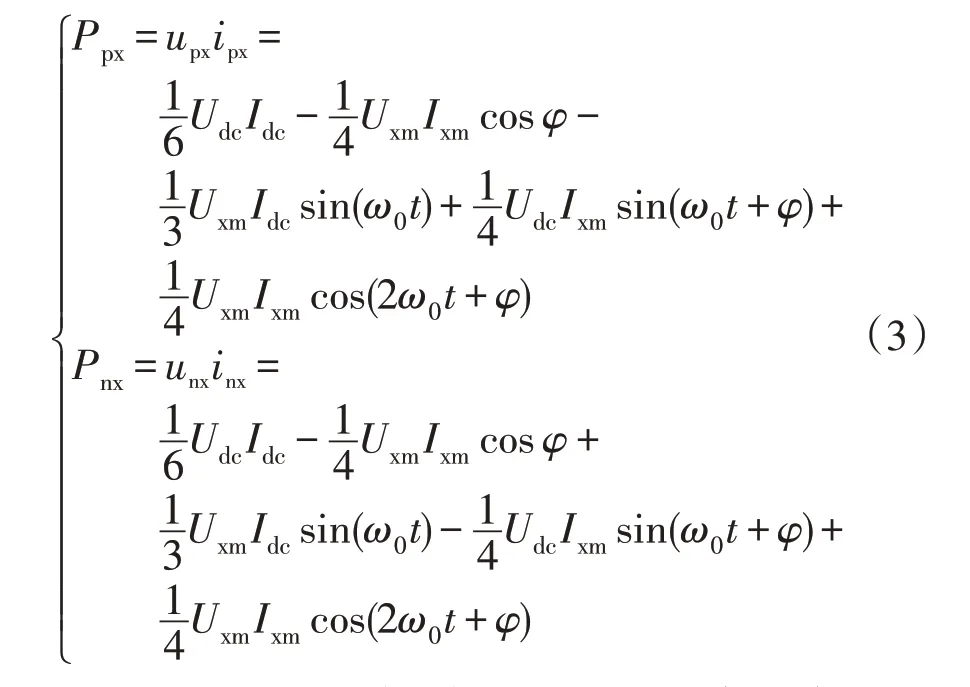
式中，前两项分别为各桥臂有功功率的直流表示方法与交流表示方法，均为换流站传输有功功率的六分之一，其代数和为0；第3 项和第4 项为基频交流波动量，在各相上、下桥臂之间流动；第5 项为二倍频波动量，在各相之间流动。故各桥臂的能量波动只需要考虑功率的交流分量，可以表示为

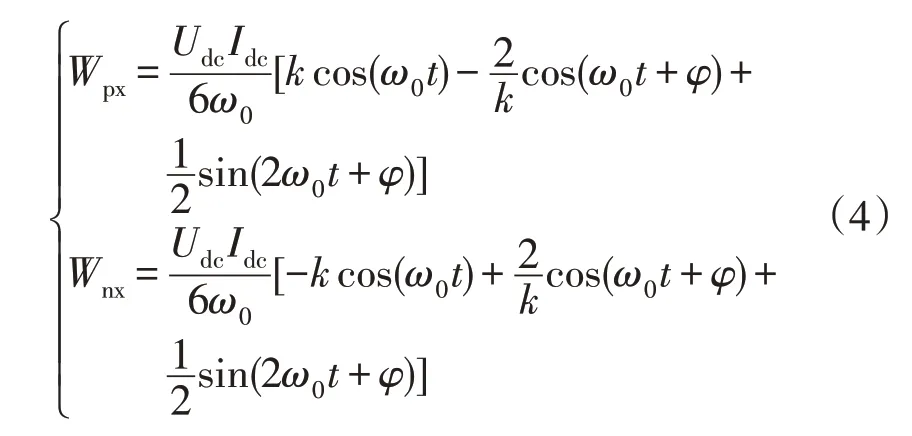
式中k为调制比，取值为

公式（4）中桥臂能量波动由中括号内部变量引起，将内部公式加和值命名为波动因子，波动因子大小决定桥臂能量波动量。单个周期内波动因子大小与调制比k的关系见图2。

图2 波动因子Fig.2 Fluctuation factor

根据图2 可知，无功功率Q对波动因子有一定的影响，当调制比较小时，波动因子随Q的增加而减小，当调制比较大时，波动因子随Q的增加而增大，但总体来看，Q对波动因子的影响远小于调制比k。同时，可以定性得出不同无功功率Q下的波动因子均在调制比为1.4 左右时振幅最小，即桥臂能量在单个周期内波动幅值最小。

2 子模块设计与调制比确定

当调制比取值大于1 时，阀侧交流相电压峰值大于0.5Udc，各桥臂电压出现负值，见图3。

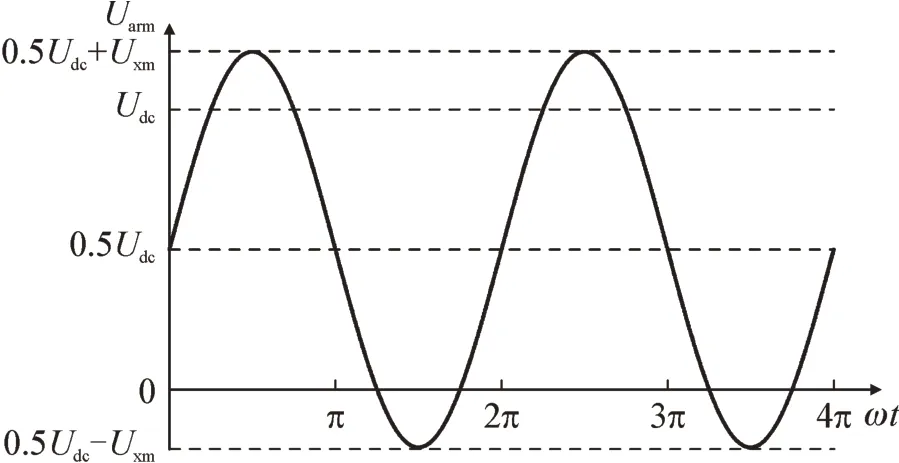
图3 各桥臂电压示意图Fig.3 Schematic diagram of each arm voltage

为实现桥臂输出负电压，各个桥臂需要配备两种改进接线方式的子模块，见图4。各个子模块在电容器两端留下接线端口。

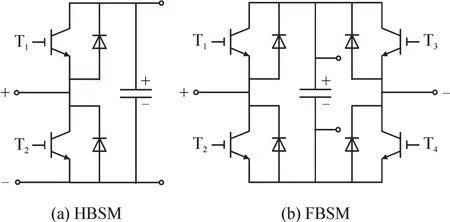
图4 子模块的两种接线方式Fig.4 Two wiring methods of sub-module

HBSM 配备N个，每个子模块电容电压UC为Udc/N，用来稳定直流电压。FBSM 配备M个，M与N的关系式为

M用来维持各个桥臂过调制部分的电压。

当交流电压大于Udc/2 时，上桥臂HBSM 全部投入的同时，上、下桥臂FBSM 分别以输出UC和-UC状态投入；当交流电压小于-Udc/2 时，下桥臂HBSM全部投入的同时，上、下桥臂FBSM 分别以输出-UC和UC状态投入。

实际各个桥臂包含HBSM 和FBSM 共0.5（k+1）N个，若k取值增大，虽然能够保证各个子模块电容减小，进而保证子模块体积减小，但增加了子模块数量，换流阀塔体积增减未能确定，所以需要找到合适的k值使得换流阀塔体积降为最低。

子模块电容体积与其容值正相关，降低电容能量波动幅值（波动因子幅值）能够有效降低各个子模块需要配备的电容值。因换流阀塔主要由子模块构成，所以当各桥臂的子模块数量与波动因子幅值乘积达到最小值时，即可最大程度地降低换流阀塔体积。体积与调制比关系如公式（7）所示。

公式（7）中，Gpx和Gnx分别由公式（4）的波动因子恒等变换得出，可以看出，各桥臂波动因子第1项取决于φ角，当换流器只传输有功功率时，第1项为0。若使得调制比k取值为 2 ，则第2 项为0，此时桥臂交流能量将仅剩二倍频波动量，波动幅值将大幅度降低，并且由于子模块增加而引起的体积增大问题也得到了解决。经过Matlab 分析计算，为保证不同功率运行区间，相比于原始调制比，k取 2 时换流阀塔理论下降体积百分比如表1所示。

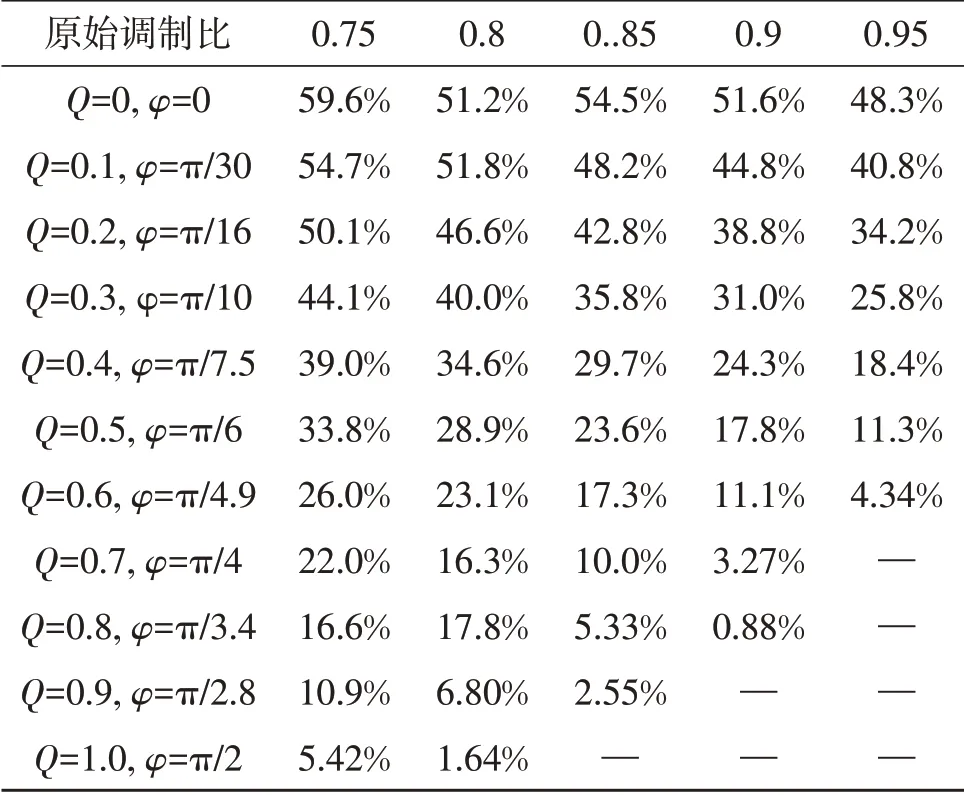
表1 换流阀理论下降体积Table 1 Theoretical descent volume of converter valve

根据公式（6），采用FBSM 的换流器子模块数量约为原换流器的1.2 倍，因为传输无功功率时公式（7）中波动因子第1 项不再为0，需要增大子模块电容才能使得无功功率顺利传输。所以如表1 所示，换流阀塔体积下降量随着系统需要传输无功功率能力的增加而减小。

柔性直流输电系统实际运行过程中主要任务是传输有功功率，无功功率只是起到对电网的电压支撑作用，需要传输无功功率的能力较小[21-28]，保证换流站可以传输一半容量的无功功率已经足够，则相比于k=0.9 换流阀塔体积至少能减小20%。

3 子模块调制策略设计

换流器仍采用最近电平逼近调制策略，见图5，输入值为内环电流控制器的输出值，uref波形应与图3 保持一致。

图5 最近电平逼近调制Fig.5 Nearest level approximation modulation

HBSM 和FBSM 电容电压分离排序，在±Udc/2区间以内的各相交流电压由HBSM 进行拟合，在±Udc/2 区间以外的各相交流电压由FBSM 进行拟合。

3.1 HBSM投切控制

当桥臂电流大于零时投入电容电压最低的子模块或切除电容电压最高的子模块，当桥臂电流小于零时投入电压最高的子模块或切除电容电压最低的子模块。

3.2 FBSM投切控制

FBSM 保持T1常通，T2常闭，T3和T4交替导通即可实现UC和0 电平的切换；保持T1常闭，T2常通，T3和T4交替导通即可实现-UC和0 电平的切换。

当FBSM 输出正电平时的投切规则和HBSM相同。

当FBSM 输出负电平时的投切规则如下：

当桥臂电流大于零时投入电容电压最高的子模块或切除电容电压最低的子模块，当桥臂电流小于零时投入电压最低的子模块或切除电容电压最高的子模块。

各子模块投切控制流程图见图6。

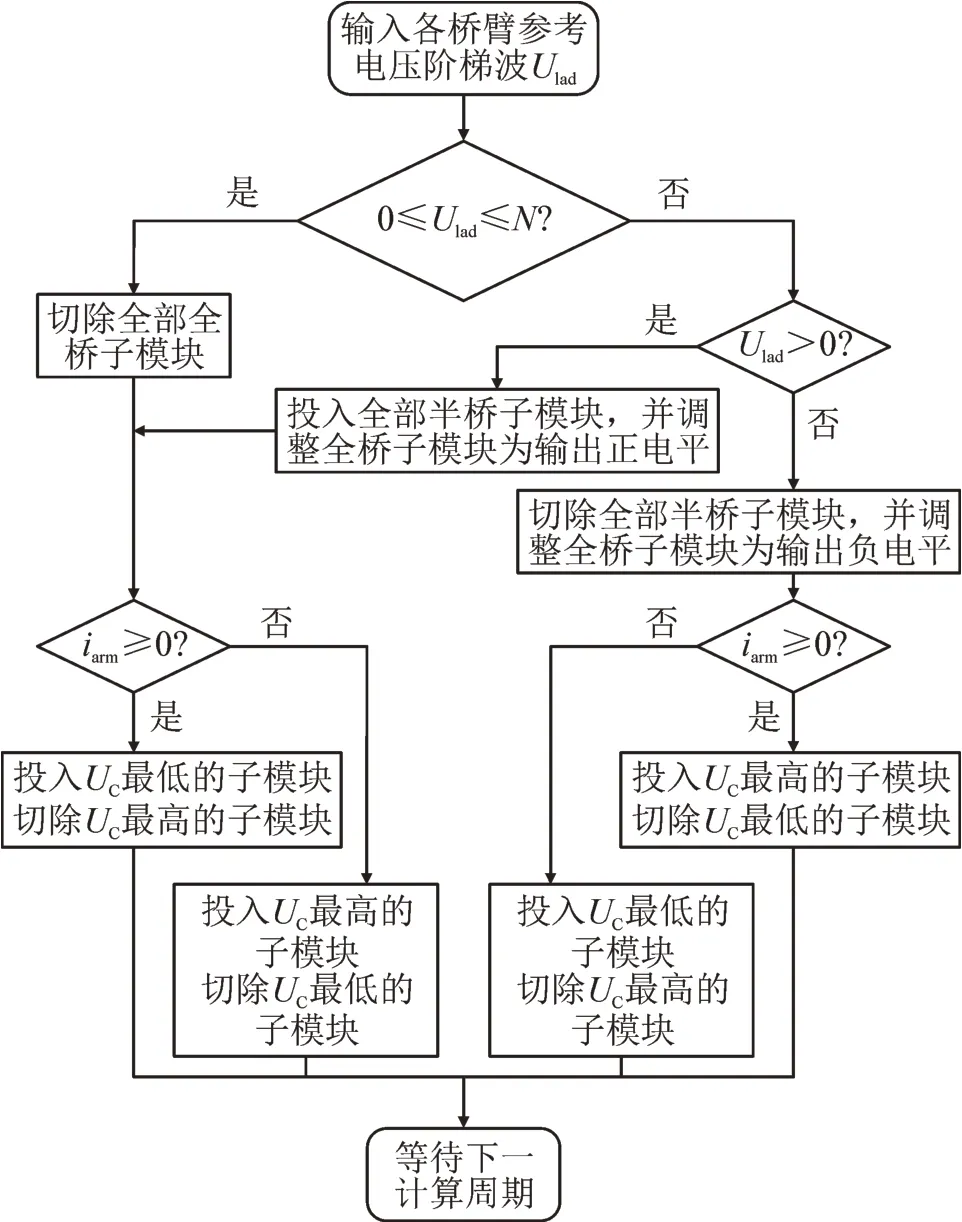
图6 子模块投切控制流程Fig.6 Switching control flow of sub model

4 换流器主电路设计

据上述方案进行了仿真模型搭建，发现HBSM电容电压波动较小，约为额定值的±3%，但FBSM电容电压波动较为剧烈，见图7。分析原因得出，当系统传输有功功率时，输出负电平的FBSM 电容大部分时间都处于放电状态或大部分时间都处于充电状态，导致其电容电压一直降低或升高，直至HBSM 开始投入，FBSM 电容电压才能逐渐恢复。

图7 子模块电容电压Fig.7 Capacitive voltage of sub model

由三相桥臂电容电压波动的相序关系可知，当B 相FBSM 投入为负电平且电容电压处于波谷时，A 相HBSM 电容电压基本处于波峰状态。可以利用这两者的互补关系，降低FBSM 的波动量，即A相HBSM 与B 相FBSM 互补，B 相HBSM 与C 相FBSM 互补，C 相HBSM 与A 相FBSM 互补。

为实现电容电压互补，图8 给出了A、B 两相之间的接线方式，BC、CA 接线方式以及下桥臂各相接线方式与图8 相同。

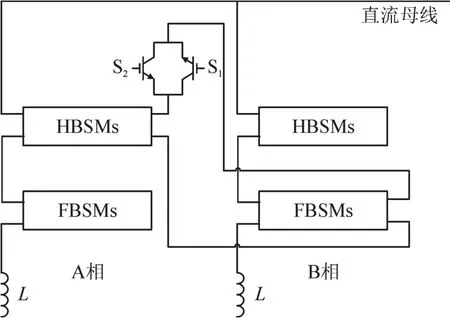
图8 电容电压互补电路图Fig.8 Capacitive voltage complementary circuit diagram

图8 中HBSMs 为各桥臂半桥子模块群，FBSMs为各桥臂全桥子模块群。HBSMs 和FBSMs 左侧端口由图4 中各自子模块端口串联而成，右侧端口由图4 中各自子模块电容端口串联而成，即实现N个HBSM 对M个FBSM 的补偿。S1和S2两个IGBT 开关管控制着互补电路的通断与导通方向。

当B 相FBSM 以负电平的形式投入运行后，阀基控制器计算该桥臂FBSM 电容电压平均值，若平均值小于0.99UC，则导通S1，用电压即将上升至波峰的A 相HBSM 电容给其充电；若平均值大于1.01UC，则导通S2，令其给即将下降至波谷的A 相HBSM 电容充电。同理，其他桥臂也采用此方法进行电压互补。

互补电流直接作用于电容，导通回路是互补电路，不会流入桥臂，不影响交直流系统的运行状态，属于换流器内部的子模块均压过程。

5 仿真验证

为验证所提出的电容电压波动抑制方法以及调制策略，在Matlab/Simulink 平台上搭建了容量为1 500 MW 的±250 kV 柔性直流数字仿真系统，分别采用纯半桥型换流站和半桥全桥混合型换流站进行对比仿真。

仿真工况1：换流器由纯HBSM 组成，系统参数见表2，调制比为0.816，当系统满容量传输时，子模块电容电压波形见图9，可见为使电容电压波动量维持在额定值的5%以内，子模块电容至少需要设置为6 000 μF。

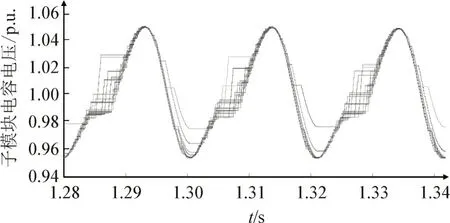
图9 HBSM电容电压Fig.9 Capacitive voltage of HBSM

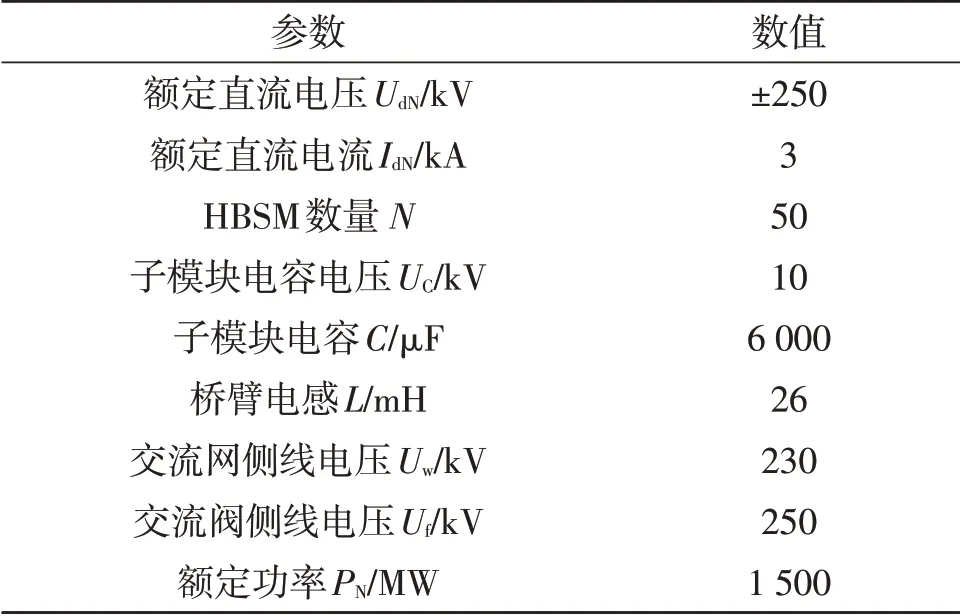
表2 直流系统仿真参数Table 2 Simulation parameters of DC system

仿真工况2：换流器由半桥全桥混合子模块组成，系统参数见表3，调制比为1.414，当系统Q=0.5，φ=π/6 满容量传输时，子模块电容电压波形及换流器三相上桥臂互补电路电流见图10，可见子模块电容降低至4 000 μF 时，电容电压波动量仍能维持在额定值的5% 以内，电容体积下降了三分之一。同时互补电路电流峰值约为150 A，远远小于各个桥臂流过的工作电流。

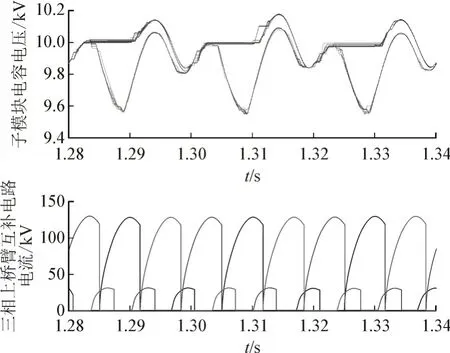
图10 HBSM和FBSM电容电压及互补电路电流Fig.10 Capacitive voltage and complementary circuit current of HBSM&FBSM

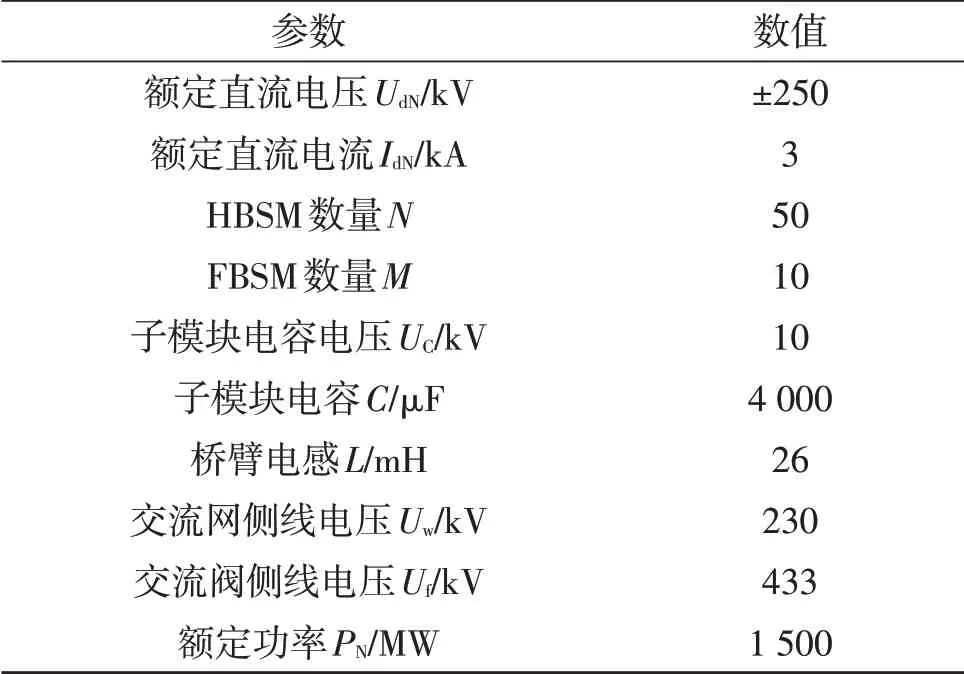
表3 直流系统仿真参数Table 3 Simulation parameters of DC system

换流器解锁后升功率阶段的波形见图11，电压波形为标准正弦波，电流上升平稳并能够较快速地达到稳态，新增的互补电路对换流器正常运行时的动态性能无异常影响。

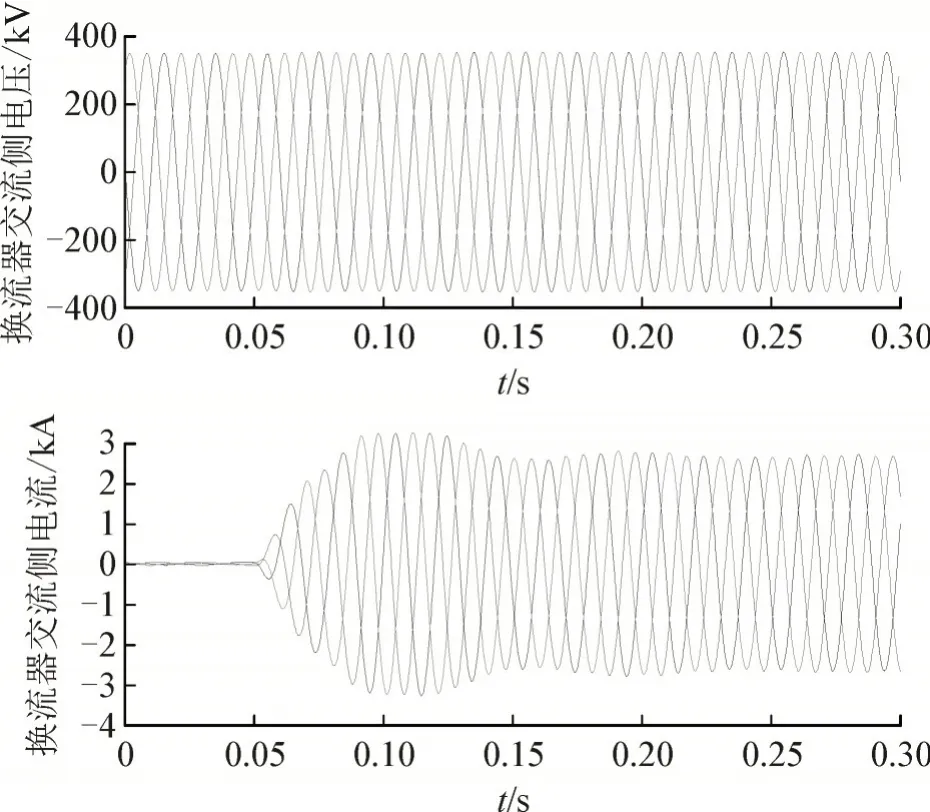
图11 换流器交流侧电压及电流Fig.11 Voltage and current at AC side of converter

6 结语

1）本文分析了各相上下桥臂能量关系式，得出了子模块电容电压波动量与调制比强相关；提出了一种HBSM 和FBSM 相结合的方式来降低子模块电容波动量，推导能量波动因子，得出调制了比为时，子模块电容可以取得最小值。

2）针对FBSM 以负电平形式投入后电容电压波动较大的问题，提出了电容电压互补的均压控制方式，用本相HBSM 电容电压与后一相FBSM 电容电压进行互补，以降低FBSM 电容电压的波动。

3）搭建了1 500 MW 的±250 kV 柔性直流数字仿真系统，分别采用纯半桥型换流站和半桥全桥混合型换流站进行对比仿真，仿真结果表明采用本文提出的电容电压抑制方法可以相比于调制比为0.816 的柔直系统可以使电容值下降1/3，与前文计算得出的百分比基本一致。