MMC-HVDC 环流频率自适应重复控制策略研究

石超，夏向阳，刘远

（长沙理工大学电气与信息工程学院，长沙 410114）

0 引言

基于模块化多电平换流器的柔性直流输电系统（MMC-HVDC）具有远距离输电成本相对较低、有功及无功功率控制灵活等优点，是未来大规模远距离输电的主要手段之一[1-3]。

由于MMC 拓扑结构的特殊性，模块电容均压以及桥臂环流控制成为了MMC 稳定运行的首要考虑因素[4-6]。其中模块电容的均压可以通过控制桥臂能量平衡实现，桥臂能量控制器输出的环流参考值中包括直流分量和交流分量[7-9]，因此在设计桥臂环流控制器时，需要考虑控制器跟踪多频率分量的能力。基于内模原理的重复控制器可以准确跟踪周期性信号及倍数次谐波，特别适应于控制桥臂环流，但其在暂态过程中，由于重复控制器延迟一个周波输出，其调节速度很慢，需要和动态响应较快的控制器配合使用[10]。文献[11]提出了一种由PI 控制器和重复控制器并联组成的环流抑制方法，可实现对不同偶次环流分量的有效抑制，但两者间的设计参数会相互影响。文献[12]提出了一种由PI 控制器与重复控制器串联组成的嵌入式重复控制器，能够有效实现对环流各谐波分量的抑制，相比并联的结构效果更好，且参数可以独立设置。文献[13]提出了一种基于重复控制原理的模型预测控制策略，通过求解MMC 的最佳开关状态来抑制环流。

上述策略大都是在MMC-HVDC 稳定运行状态下提出的环流抑制策略，而针对风电场在经MMCHVDC 并网时线路频率变化对环流抑制影响的研究较少。由于风电具有随机性和间歇性等特征，对于采用分散控制的大规模风电场，在利用下垂特性调节单个风机的有功出力时，可能会引起海上交流电网频率的变化[14-15]，导致系统采样频率与电网频率比值可能不为整数，因而文献[13-15]等针对特定频率的重复控制器性能会受到影响。为此文献[16]提出了一种基于无差拍控制和重复控制组成的MMC 桥臂电流控制策略，其利用三阶拉格朗日插值法逼近非整周期延时，并给出了设计思路、参数设计方法。文献[17]提出了一种基于空间相位采样技术的MMC 环流频率自适应策略，以基本空间相位的倍数对系统进行采样，确保每个周期的采样个数能够保持不变，解决了系统频率偏移带来的影响。文献[18]根据电网频率的变化来改变系统采样频率，从而使得频率比值N一直为整数。

本文在嵌入式重复控制器的基础上，利用有限脉冲响应（FIR）滤波器，通过在线调整FIR 滤波器的系数实现分数延迟，使得嵌入式重复控制器的谐振频率更接近电网频率，并给出了控制器的设计思路、参数设计方法，同时对其稳定性进行了深入分析。最后通过Matlab/Simulink 仿真验证了所提策略的有效性。

1 MMC拓扑结构及其数学模型

三相MMC 由3 个相单元组成，其拓扑结构见图1。一个相单元包括上下两个桥臂（p 表示上桥臂、n 表示下桥臂），每个桥臂由N个半桥子模块（sub module，SM）和桥臂电抗Lc（桥臂电感L0和桥臂损耗等效电阻R0）串联组成；upj、unj分别为换流器上下桥臂投入运行的子模块电容电压之和：ipj、inj为换流器上下桥臂电流；usj、ij为交流侧各相电压和电流；udc、Id分别为直流侧电压和电流，其中j=a、b、c。

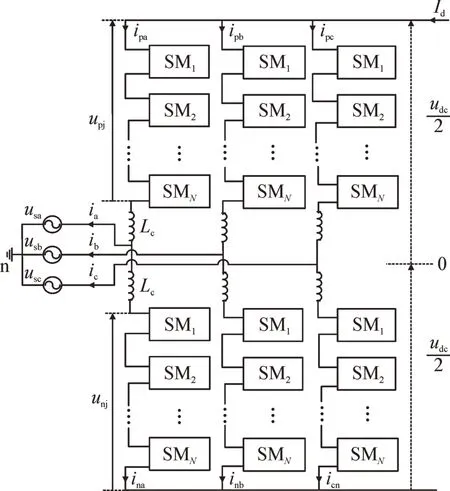
图1 三相MMC拓扑结构Fig.1 Topology of three phase MMC

根据MMC 的电路结构和基尔霍夫定律，可以得到公式为

定义环流公式为

根据瞬时功率理论，由式（1）可得上桥臂和下桥臂的瞬时功率公式为

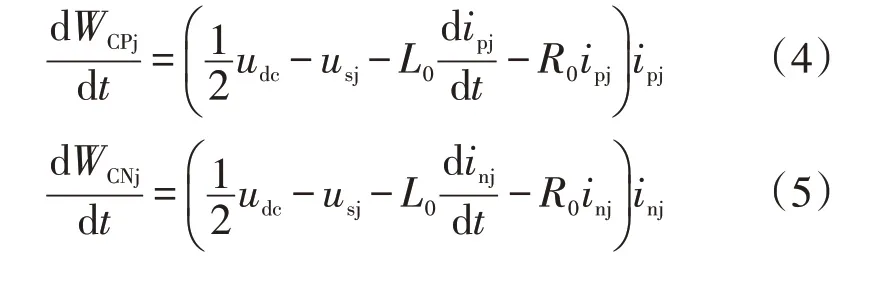
2 环流参考值计算

MMC 正常运行及交流电网频率波动时都需要保证电容电压的平衡，因此在计算桥臂环流参考值时要兼顾子模块电容电压的平衡[19-24]。而桥臂中的能量都存储在子模块的储能电容中，因此可以通过对MMC 桥臂能量进行控制来平衡三相桥臂子模块的平均电容电压，有关MMC 的电容电压平衡策略已有大量文献进行了研究，本文以文献[25]提出的桥臂能量控制为基础计算得到环流参考值，下面进行简单介绍。

2.1 上下桥臂能量和控制

系统稳定运行时，忽略子模块电容电压纹波的影响，假设电容电压近似相等，则上桥臂和下桥臂子模块电容中的能量可以表示为

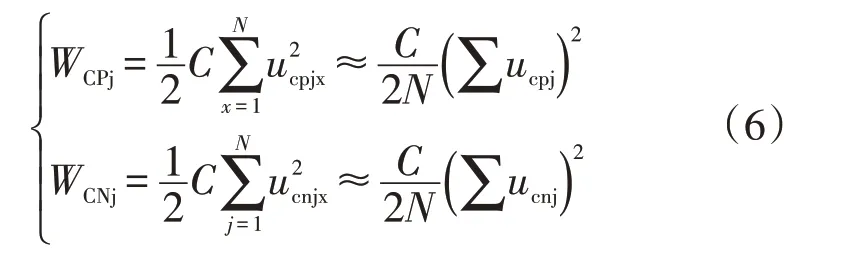
式中：ucpjx为j相上桥臂第x个子模块的电容电压；ucnjx为j相下桥臂第x个子模块的电容电压；ucpj、ucnj分别为j相上下桥臂的平均电容电压。

则j相上下桥臂能量之和、之差可以表示为

对式（4）、式（5）相加，可得到上下桥臂瞬时功率之和为

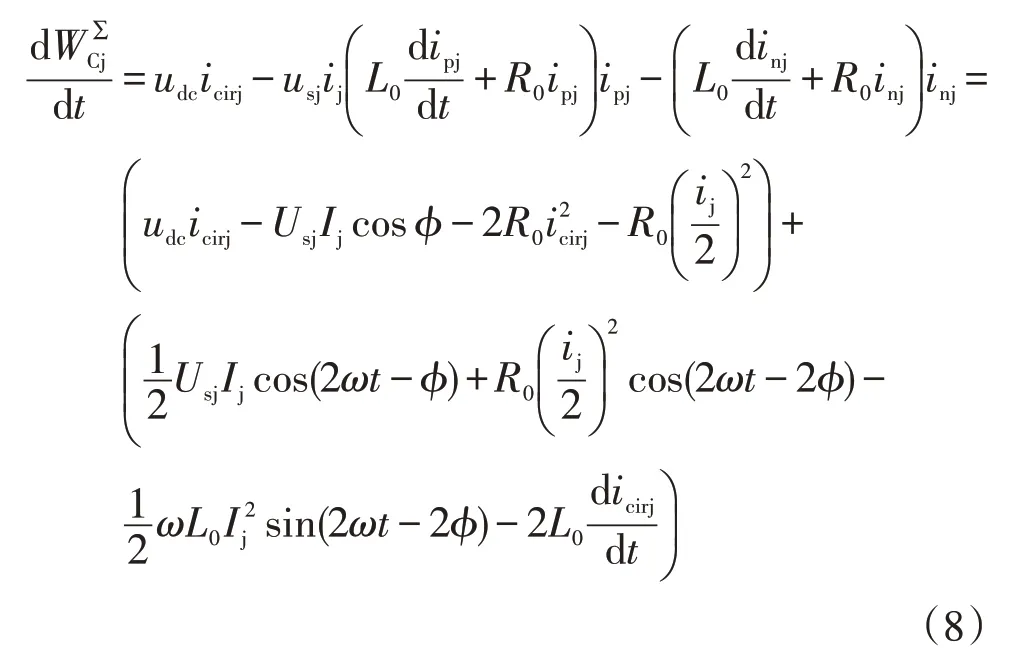
忽略桥臂阻抗R0上的损耗，考虑环流中的直流以及低次谐波分量（主要是二倍频），对上述功率表达式进行归类得：

式中：数字下标（0、2、4）为功率对应的几次脉动成分；φ为交流侧功率因数角；Usj、Ij为交流侧电压和电流的幅值。

本文选用梳状滤波器，梳状滤波器是由许多按一定频率间隔相同排列的通带和阻带，只让某些特定频率范围的信号通过。

假设系统采样频率为fs，基频频率为fg，则数字梳状滤波器的离散传递函数可由下式给出

同时为了增加梳状滤波器对频率变化的适应性，在系统采样频率与电网二次谐波频率比值不为整数时需要对Ns进行取整处理，常用的取整方法包括四舍五入、向上取整、加权平均等。向上取整误差较大，加权平均法对硬件的瞬时运算要求较高，本文综合考虑计算量和实现效果选择四舍五入取整方法[26]。

滤波电路的频率响应见图2，观察发现其对偶次谐波都有很高的衰减。

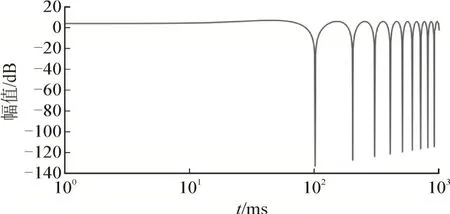
图2 梳状滤波器的频率响应Fig.2 Frequency response of spatial filtering

2.2 上下桥臂能量差控制

考虑到上下桥臂损耗不等时，需要控制上下桥臂子模块电容电压的平衡。同理，对式（4）-（5）做差得到上下桥臂瞬时功率之差的表达式为

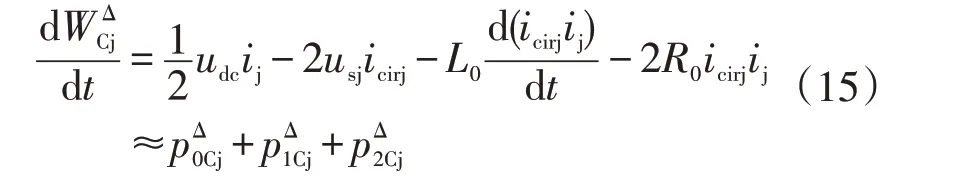
如果只考虑环流icirj中的直流分量Icirj，则式（15）可以简化为

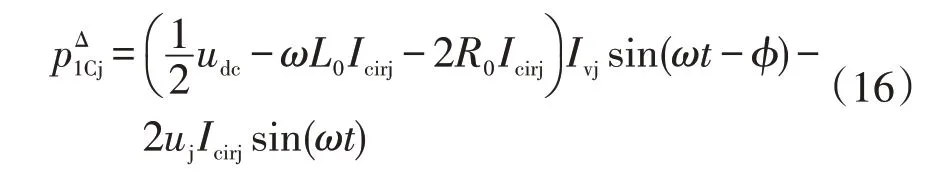
假设环流中基频分量表示为

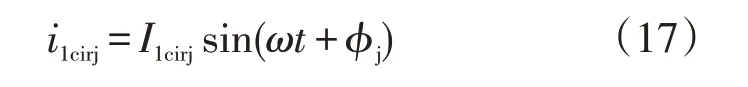
则式（9）中的直流功率部分可以表示为

当上下桥臂的能量不平衡时，可通过pΔ0Cj进行合适补偿以重新实现上下桥臂能量的平衡，选择I1cirjcosφj作为差分能量控制器的输出。

根据上述分析，可以得到基于能量平衡的环流参考值计算过程见图3。

图3 桥臂能量控制Fig.3 Energy control of bridge arm

3 基于FIR滤波器的嵌入式重复控制器设计

3.1 分数延迟FIR 滤波器的设计

由于电网频率的变化，可能导致采样频率与电网二次谐波频率之比Ns非整数，而控制算法一般在数字控制系统中实现，无法实现非整倍数周期的延时，只得忽略小数部分，这会降低系统的开环增益，产生较大的稳态误差，影响重复控制器的控制性能。

当Ns为非整数时，Ns可以分为整数部分N和分数部分F，公式为

其中分数延迟N-F可以通过基于拉格朗日插值法的FIR 滤波器实现，M阶FIR 滤波器的结构见图4，分数阶延迟传递函数可以表示为

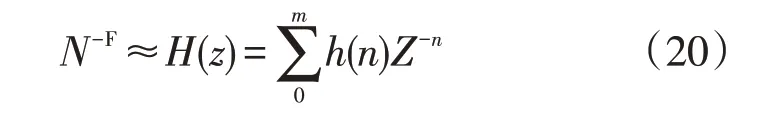
图4 M阶FIR滤波器的实现Fig.4 Realization of M-order FIR filter

本文采用三阶拉格朗日多项式逼近小数部分N-F，其可以表示为

例如z-201.6可以表示为

3.2 嵌入式重复控制器设计

在电网频率变化时，本文利用FIR 滤波器实现分数阶延迟，对重复控制器内模中的Ns修正为整数部分N和小数部分F，使得嵌入式重复控制器谐振频率近似于电网频率，从而达到适应电网频率变化的目的。

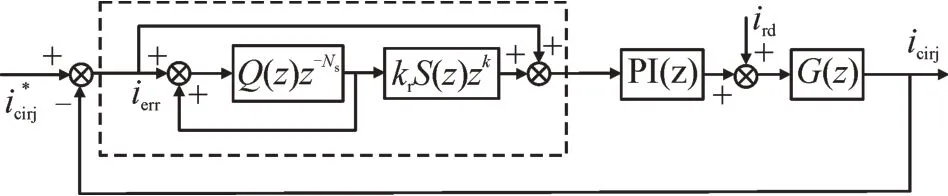
图5 嵌入式重复控制器的结构Fig.5 Structure of embedded repetitive controller

从误差信号到指令信号的传递函数可以表示为

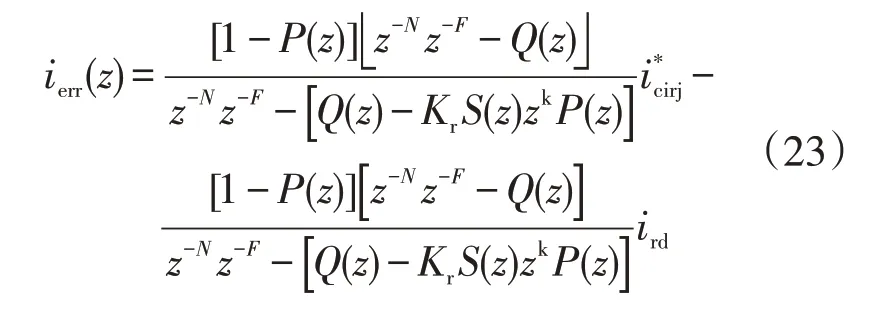
式中

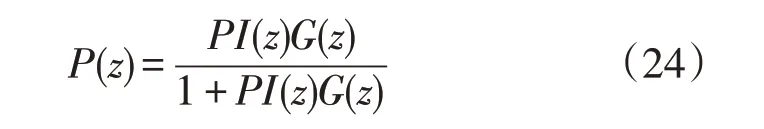
G(z)经过ZOH 离散化为

PI 控制器的z传递函数为

式中，比例项kp=20、ki=80。

内模Q(z)是重复控制器的重要环节，由于Q(z)对积分效果有一定减弱，通常选小于1 的常数或者零相低通滤波器，本文选零相移低通滤波器，其表达式为

重复控制补偿环节KrS(z)zk由3 部分组成，其中Kr为重复控制器的增益，S(z)为滤波器，超前环节zk为S(z)P(z)提供相位补偿。

S(z)的作用是使S(z)P(z)在中高频段的增益要快速衰减，而在中低频段的增益为1，从而保证控制系统的稳定性。

本文选用二阶低通滤波器，取自然频率ωn=10ω1，阻尼比ξ=1，伯德图见图6，表示该滤波器在高频段增益衰减迅速，提高了系统的稳定性。

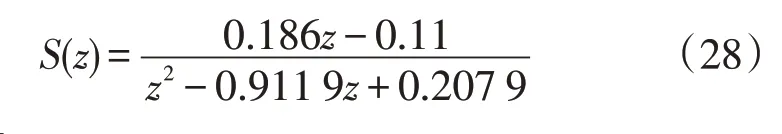
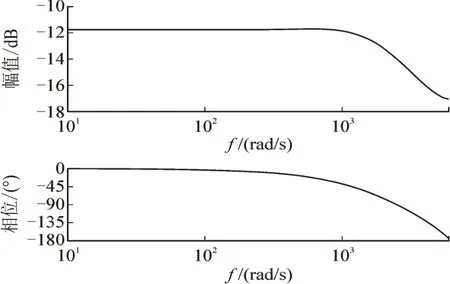
图6 S（z）的伯德图Fig.6 Bode diagram of S（z）

超前环节zk用于相位补偿。环流中主要以偶次谐波为主，次数越高，谐波含量越低，因此本文设计参数时所关心的频率为低于1 000 Hz 的频段，经试验k 取6 效果最好，伯德图见图7，其能够有效抵消S(z)P(z)的相位滞后。

图7 S（z）P（z）与zk 的相频特性Fig.7 Phase frequency characteristics of S（z）P（z）and zk

重复控制器的增益Kr(0 ＜Kr＜1)对系统的稳定性和响应速度非常重要，Kr和稳定裕度成反比，但稳定裕度越大，误差的收敛速度越慢。

根据式（23）得到重复控制系统的特征方程为

要保证重复控制系统的稳定性，上述特征方程的根应该都要落在以原点为圆心的单位圆内，但是直接对特征根进行求解比较困难，可以通过小增益原理对上式进行分析，判断系统稳定的条件。

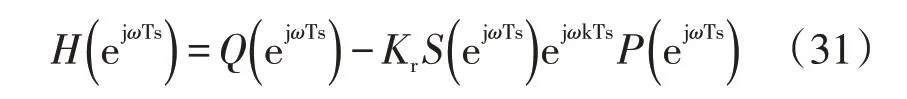
定义误差收敛指数为

经试验，当增益Kr=1 时，控制系统的奈奎斯特图轨迹的起始端距离单位圆较远，拥有较高的稳定裕度，对于二倍频有较高的谐波抑制性能。

为了分析电网频率变化对嵌入式重复控制器性能的影响，图8 为普通嵌入式重复控制和基于FIR 滤波器的嵌入式重复控制在电网频率正常（50 Hz）和频率波动（49.7 Hz 或者50.3 Hz）时二次谐波处的频率特性。观察发现当电网频率由50 Hz 变为49.7 Hz 或者50.3 Hz 时，由于普通重复控制器由于无法实现分数阶延迟，导致其在实际谐振频率处的增益下降，增加了系统的跟踪误差。而基于FIR 滤波器的复合重复控制系统在谐振频率处仍然保持高增益，不受电网频率波动的影响。

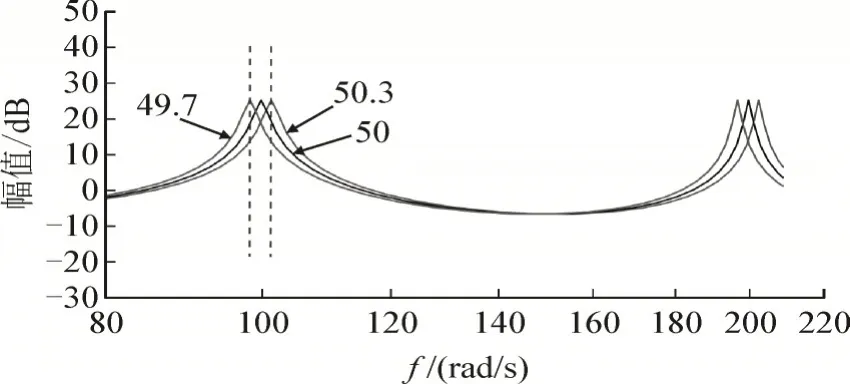
图8 电网频率波动时二次谐波处重复控制的幅频特性Fig.8 Amplitude-frequency characteristic of repeated control of second harmonic in frequency fluctuation of power grid

4 仿真分析

为了验证本文所提控制策略的有效性，利用Matlab/Simulink 软件平台搭建了51 电平双端MMC-HVDC仿真模型，模型的相关参数见表1。

表1 仿真平台主要参数Table1 Main Parameters of simulation platform

4.1 系统正常运行时仿真结果

首先验证系统正常运行时本文桥臂能量控制和环流控制策略的有效性。图9（a）-图9（b）分别为不采用桥臂能量控制时的a 相上桥臂、下桥臂子模块电容电压平均值和abc 三相桥臂子模块电容电压平均值，图10（a）-图10（b）为采用桥臂能量控制对应子模块电容电压平均值。

观察发现当系统稳定运行时，两者的电容电压都稳定在额定电压2 700 V 附近波动，但未加桥臂能量控制时，a 相上桥臂子模块平均电容电压和a 相下桥臂子模块平均电容电压的波动幅值不相等，a、b、c 三相桥臂的子模块电容电压的波动幅值也存在一定的差值，如图9 所示；相比之下加入桥臂能量控制时子模块电容电压的均压效果更好，波动幅值基本上相等，如图10 所示。

图9 未加桥臂能量控制时子模块平均电容电压Fig.9 Average capacitive voltage of sub module without adding bridge arm energy control

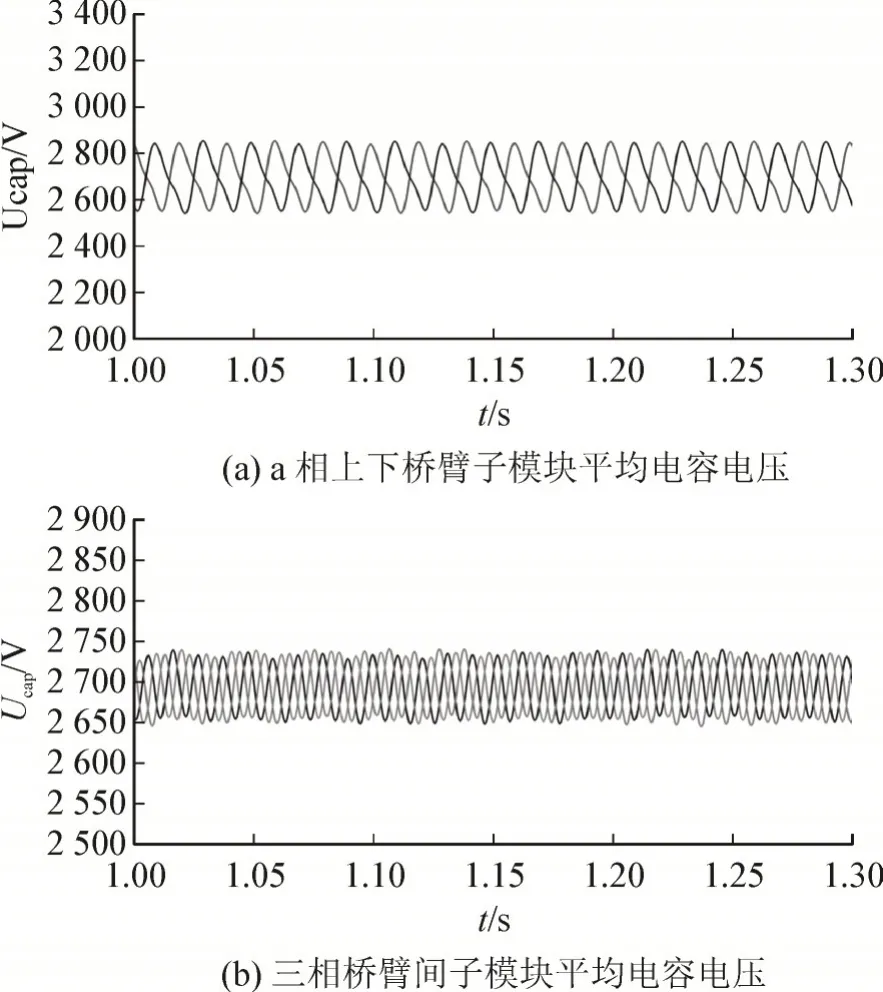
图10 加入桥臂能量控制时子模块电容电压Fig.10 Capacitive voltage of sub module with adding bridge arm energy control

系统正常运行时桥臂环流以二倍频、四倍频等偶次谐波为主，传统的环流抑制策略通过对环流进行二倍频负序坐标变化，设置其d 轴和q 轴参考值为0，采用的是PI 控制器。图11（a）为采用传统环流抑制策略（CCSC）时a 相桥臂环流抑制的效果，在1.4 s CCSC 投入后，环流得到了一定抑制，幅值明显下降，但仍然存在较大的环流；图11（b）为采用本文所提嵌入式重复控制器的效果，同样在1.4 s 时投入，通过对比可以发现嵌入式重复控制器相比传统环流控制器的抑制效果更好。

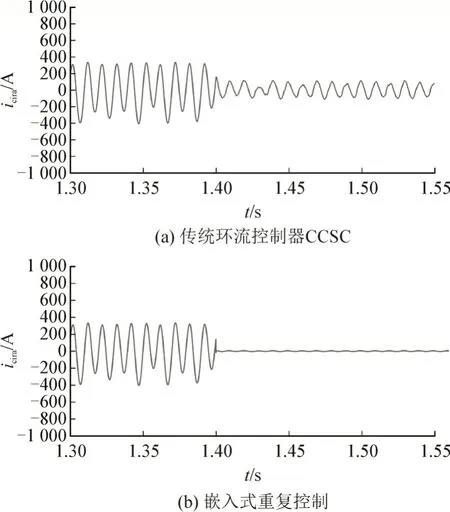
图11 环流抑制效果Fig.11 Suppression effect of circulation

4.2 频率变化时仿真结果

当交流电网频率发生波动，在1.6 s 电网频率由50 Hz 变为49.7 Hz 时，交流侧三相电流如图12（a）所示，基于有限脉冲滤波器（FIR）的嵌入式重复控制环流抑制效果如图12（b）所示。

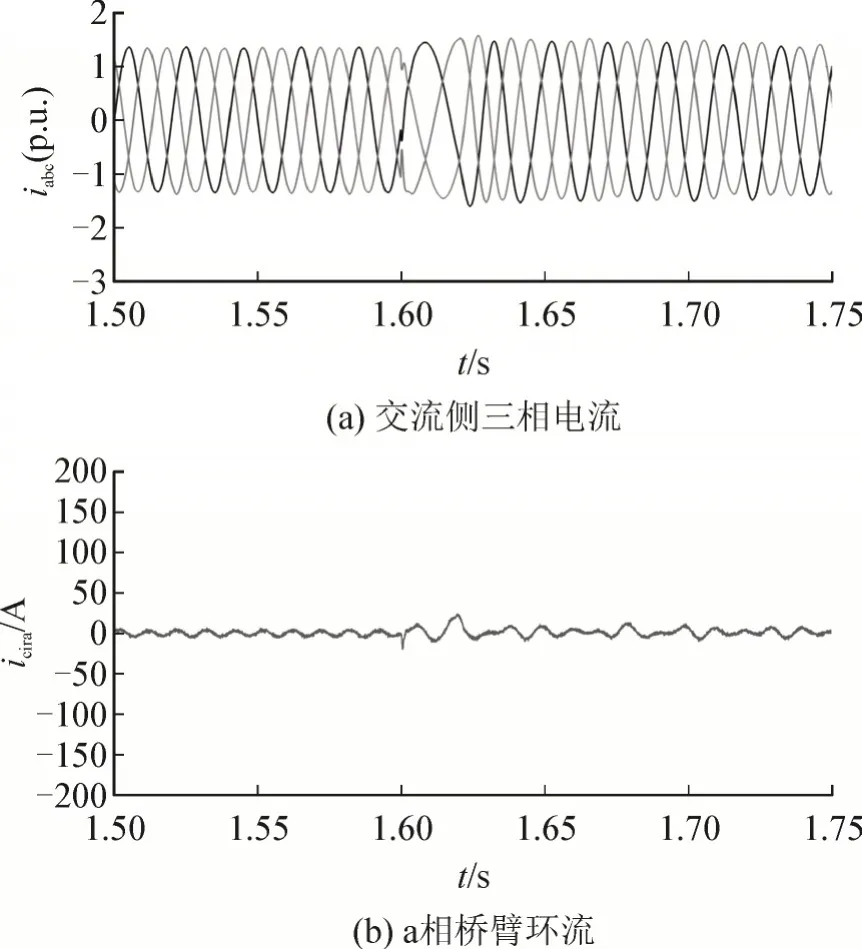
图12 频率变化时仿真结果Fig.12 Simulation results in frequency variation

由于嵌入式重复控制器从系统开始运行时就一直投入，因此环流一开始就得到了抑制，当1.6 s时电网频率发生波动，此时系统采样频率与电网频率的比值不为整数，通过调节FIR 滤波器的参数实现分数阶延迟，使得嵌入式重复控制器自适应电网频率。因此环流的幅值稍微增大后趋于稳定，但仍然处于一个较小的范围，表明所提控制策略在频率变化下仍然能够有效抑制环流。

5 结语

本文提出的MMC-HVDC 环流频率自适应重复控制策略由环流参考值计算环节和基于有限脉冲响应滤波器（FIR）的嵌入式重复控制器组成，通过分析与仿真得到如下结论：

1）维持MMC 中能量平衡是系统稳定运行的重要条件，通过控制MMC 中上下桥臂能量之和、能量之差，同时加入梳状滤波器能够得到维持子模块电容电压平衡的精准环流参考值。

2）通过在线调整FIR 滤波器的系数实现分数阶延迟，能够使得嵌入式重复控制器的谐振频率更接近电网频率，即使在交流侧频率发生波动的情况下，也能够有效抑制环流中的谐波分量，并通过仿真验证了本文所提策略的有效性。