冲突射频识别标签分离的似然解码*

桂妮霞吴海锋李 毅曾 玉陈跃斌

(1.云南民族大学 电气信息工程学院，云南 昆明650500；2.云南省高校智能传感网络及信息系统科技创新团队，云南 昆明650500)

无线射频识别(Radio Frequency Identification，RFID)技术是一种利用无线电波让标签和阅读器可进行数据交换的自动识别技术。 RFID 系统根据标签的工作方式可分为主动式和被动式，根据工作频率不同又可分为30 MHz～300 kHz 的低频、3 MHz～30 MHz 的高频和300 MHz～968 MHz 的超高频(Ultra High Frequency，UHF)系统[1]。 由于被动式UHF 系统具有读写距离远和标签结构简单等特点，因此已逐渐成为物联网前端传感部分的主要技术，在物联网应用中得到了普遍的关注。

UHF RFID 技术应用于物联网时，需要同时识别多个标签以提高识别效率，由于标签传输数据共享同一无线信道，因此标签冲突难以避免，而防冲突是解决标签冲突的主要技术之一。 防冲突一般在介质 访 问 控 制(Media Access Control，MAC) 层 进行[2-5]，当发生冲突时，标签信号重新发送，当冲突增多，重发也增多，因此识别效率并不高。 物理层的分离技术[6]可从冲突信号中直接恢复标签信号，减少了重发次数，因此有效地提高了识别效率，近年来也一直被应用于RFID 标签防冲突中。 信号编码作为一种通信技术可有效地抵抗干扰信号，而防冲突实质也是一种抗干扰技术，因此良好的编码可提高RFID 标签在物理层的防冲突性能。

频率漂移在无线通信中是一普遍现象，UHF RFID 中发生频率漂移同样难以避免，这使得传统的匹配滤波器[7]难以完成较好的解码过程。 作为现存应用较为广泛的UHF RFID 标准之一，EPC C1 Gen2[8]规定信号可使用FM0 和Miller 编码，由于这些解码主要通过相位是否改变来判断码元，而无需确切知道码元频率周期，因此可较好地解决频率漂移的解码问题[9]。 特别Miller 码相比FM0 码，不仅有相位跳变还有副载波，这使得Miller 码具有更好的抗噪声性能。 然而，副载波的存在也使Miller 编解码比FM0 码更为复杂。

目前，大多RFID 物理层防冲突技术多集中在FM0 码[10-12]，本文将研究优化Miller 编解码来提高RFID 标签防冲突性能。 张吉兴等[13]提出通过计算码元个数和周期来进行解码，然而会受到频率漂移的影响导致解码失败。 Lu 等[14]通过与时钟信号按位异或来去除副载波，再通过相位跳变进行解码[15]，然而在物理层分离冲突标签时会产生分离误差，去除副载波后，分离误差仍然存在，这使得相位跳变信息不再准确，从而导致误码率增高。

针对上述的问题，本文提出一种适用于物理层分离的Miller 解码方法，利用最大似然的Viterbi 算法完成，来优化传统的Miller 解码，使该方法在防标签冲突系统中能得到更好的性能。 在实验中，采用仿真标签冲突的模拟数据和一组实测Miller 码的标签冲突数据，得到该方法在10dB 时几乎没有误码，在15 dB 时分离效率能达到100%，吞吐量最终能达到0.55。

1 相关工作

MAC 层冲突分解采用随机多址方法，信号随机选择时隙发送，若发生冲突则信号会重传。 然而，MAC 层方法将冲突时隙视为无效时隙，通信效率并不高。 物理层分离可将冲突时隙中的各信号进行恢复。 由于其将冲突时隙视为有效通信时隙，因此通信效率得到了提高。 冲突信号实为各信源信号的叠加信号，图1(a)中，两个信源叠加后成为冲突信号。通常，具有N个信源的二进制数字单极性码经同相正交相(Inphase Quadrature，IQ)解调后，其采样点投射至复平面后会呈现J=2N个簇[16]，由各簇中心点实部和虚部构成的复数可表示为

式中:h1，h2，…hN分别为各信号源衰减复系数。 经过聚类后，各采样点可根据式(1)的中心点分离为N个信源点，即[16]

通过式(1)和式(2)，可将冲突信号进行分离。图1(b)为两个信号源冲突信号投射至复平面的情形，其中，对于任一采样点，若其属于中心点为0，h1，h2或h1＋h2的簇，则被分解为00，01，10 或11。

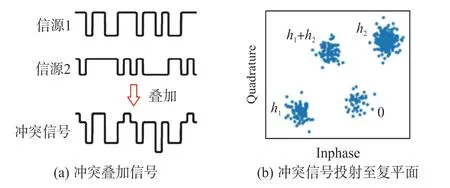
图1 物理层分离冲突信号示例

另外一种物理层分离方法根据信源的编码直接从冲突信号中解码出各个信源信号，例如FM0 码，根据其编码规则，有Kim 等[17]利用码元跳变的位碰撞算法，也有Benbaghdad 等[18]利用信号不同步完成的边缘检测算法，但是这些算法存在的问题是需要一些确定信息，当未知周期或信号不同步时，将很难完成。 也有一种方法是可将其看作一个有限状态机，利用该状态机，Viterbi 算法[19]解码可从所有搜索路径中快速寻找一条最大似然路径，以此消除其他信源对本信源的干扰，然后再用连续干扰消除逐次解码各个信源。

除FM0 码，EPC C1 Gen2 还规定UHF RFID 可采用Miler 码，图2(a)和(b)为Miller 码状态转化图及对应的码型，从图中可以看到，Miller 码与FM0 码一样可看作一个有限状态机图，但是Miller 码中每个码元包含了副载波，如图2(c)，在图中的例子，码元序列均为“010”，不同的阶数M表示不同的副载波频率，数字越大频率越高。 传统的Miller 码解码先将信号与其频率相同的副载波进行异或运算以去除副载波，再由相位跳变原则进行解码。 图2(d)给出了用该方法进行解码的例子，其中M=4，解码后得到码元“11”。

图2 Miller 编码及解码图

2 问题提出

冲突信号分离时本身带有分离噪音，如图3 中左图所示，经分离后其信号波形中将带有一些无效的相位跳变，如图3 中右图所示。 若该信号为Miller码，则通过传统的异或运算后，这些由分离噪声所带来的跳变仍然有部分无法消除。 由于Miller 解码需要判断一个码元中是否有相位跳变，因此这些无效跳变就容易产生误码。

图3 有分离噪声的Miller 副载波去除

另外，即使分离误差能够被解决，但是对冲突信号进行分离仍然存在一些不确定性。 图3 左图中两个冲突标签信号在复平面形成了四个簇，其中心点从0 开始按顺时针顺序依次为h1，h2和h1＋h2。 然而，由于每个标签信号的复衰落系数并未提前预知，其同相或正相端的系数可大可小，也可正可负，因此四个中心点的排列也可能是逆时针或其他顺序。 为确定各中心点的位置，一种直接方法是对信号衰落系数进行估计，但是无论是导频估计或者盲估计[20-22]都会增加系统的复杂度。

利用Viterbi 解码的方法无需先对信号分离，可直接从冲突信号中恢复源标签信号，但它也存在一些问题。 Viterbi 解码需要计算观测信号与搜索信号间的似然距离，通过寻找最大似然路径来找到幸存路径。 然而，若信号为单极性码波形，则搜索的路径由归一化的0 或1 表示，而搜索路径由于并未估计其第n个标签的衰落系数hn，其单极性码波形由0或hn构成，如图4 所示。 此时，若hn较小，则容易将信号1 误判为信号0，导致幸存路径的计算失败。

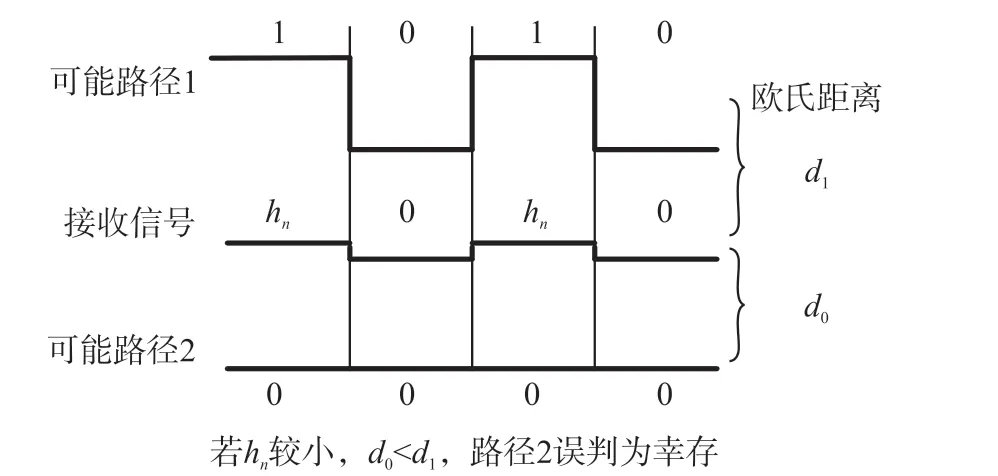
图4 似然距离计算错误示例图

3 算法

3.1 系统模型

在RFID 系统中，当有N个标签在同一时隙应答时，阅读器将会接收到N个标签的叠加信号，如图5 所示，该信号经IQ 解调后可表示为一复数信号，记为

式中:hn表示第n个标签的信道衰减系数，通常其为一平坦性衰落的时不变信道；ξ(t)是加性高斯白噪声；L为载波泄露；xn(t)代表第n个标签信号，表示为

式中:ek，n∈{0，1}K×1表示第n个标签发射的第k′个码元sk′，n∈{0，1}K′×1经编码后的码元序列，K为编码后的码元块长，K′=K/2M为标签原始码元长度，M为Miller 码阶数，例 如M=2 时，若sk′，n为1时，编 码 后 的 码 元e4k′＋1，n，e4k′＋2，n，…e4(k′＋1)，n就 为1001；an为调制脉冲波形，gn和bn分别表示码元周期和时延。

本文算法对接收的冲突信号进行解码的基本流程如图5 所示，先对接收信号进行采样，设T为采样周期，做I次采样可得接收信号矢量z=[zi]∈ℂ1×I，其中ℂ 为复数集，zi=z(iT)，i=1，2，…I。 然后，采用分离算法得到N个标签信号矢量，n=1，2，…N。最后，利用Viterbi 对解码得到标签原始码元序列矢量。

图5 系统框图

3.2 分离算法

令D=[dj]∈{0，1}J×N为行向量dj所构成的字典矩阵，其中J=2N，并有dj≠dn当j≠n，那么聚类中心矢量C=[cj]∈ℂJ×1可表示为

对于两个冲突标签的情形，字典矩阵D可表示为

由于未知信道系数H，即使已得到各聚类中心点，也无法确定与聚类中心矢量C中cj的对应关系，因此矢量C仍然未知，理论上其有种排列。为此，我们需要对C进行估计。

标签在发射其信号时有一段静默期[23]，此时有载波泄露L，如图7 所示，经采样后可确定该簇中心点c′1，表示为

另外，由EPC Gen2 可知，每个标签在发射RN16 之前均需有一段相同的前缀信号[8]，如图6，因此对于两个标签的情形可确定另一个簇中心点，表示为

图6 确定聚类中心关系图

据此，矢量C中的c1和c4可由下式进行估计

c2和c3可由剩余的两个聚类中心点确定，分别对应h1和h2，因为冲突标签数为两个，也可分别对应于h2和h1，表示为

由式(9)～式(11)可确定矢量C，进而确定式(5)，再由式(5)的字典矩阵D可得到聚类中心cj对应聚类簇Sj中各点和dj间的映射关系fdict(·)，表示为

例如，对于两个标签，若zi∈S1，fdict(zi)就为[00]，若zi∈S2，fdict(zi)就为[10]。 利用式(12)可对信号向量z进行分解，得到一个由行向量ξi构成的信号矩阵∈{0，1}I×N，其中ξi=fdict(yi)，该分解过程表示为

3.3 Viterbi 解码算法

建立似然函数

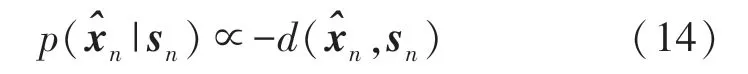
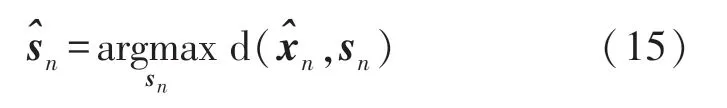
在式(15)的求解中，若对sn采用穷尽搜索，则搜索次数为2K′，计算量庞大，可采用Viterbi 解码减少其搜索次数。

由于码元sk′，n，k′=1，2，…，K′相互独立，因此可将式(15)中的似然距离改写为

图7 Miller 码网格图和解码状态波形

表1 算法步骤

4 实验设置

在本文实验中，将使用一个阅读器分离两个标签的冲突信号，RFID 阅读器和标签遵循EPC C1 Gen2 的标准，通过该通信系统来验证本文提出的算法，实验数据包含了仿真数据和实测数据。

4.1 仿真数据

仿真数据模拟了两个标签的冲突信号，由式(3)得到，具体参数设置如表2 所示。 其中，载波泄露在冲突信号中的表现更像是一个幅值常量[23]，而为了更好体现噪声对分离冲突信号的影响，仿真数据中设置的载波泄露为0。 同时，由于衰落系数的大小对传统Viterbi 解码的性能有较大影响，因此仿真数据中设置了两组不同的衰落系数，如表3 所示。

表2 仿真数据参数设置

表3 信号衰落系数设置

4.2 实测数据

实测数据来自电子科技大学信息与通信工程学院射频集成电路与系统研究中心[24]所提供的超高频RFID 系统设备，数据通过示波器进行采集，表4是实验设备的相关参数设置。

表4 实测设备系统设置

4.3 性能评价

4.3.1 算法比较

为验证本文所提算法的性能，在所有基本参数设置相同的情况下，仿真实验比较了四种算法性能，分别为M＿Viterbi、F＿Viterbi、M＿XOR 和N＿Viterbi，信号衰落系数均未知，其中M＿Viterbi 为本文提出算法，编码使用Miller 码，冲突信号分离后再使用Viterbi 解码。 F＿Viterbi 采用FM0 编码[10]，分离后采用Viterbi 进行解码[19]，将M＿Viterbi 与其对比以分析不同编码性能。 M＿XOR 采用Miller 编码，但分离后采用异或[15]解码算法，将M＿Viterbi 与其对比以分析两种解码算法的性能。 N＿Viterbi 使用Miller编码，但不分离冲突信号，直接采用Viterbi 解码，将M＿Viterbi 与其对比，以分析信号分离[16]与否对解码性能的影响。 以上算法的具体设置如表5 所示。

表5 各算法设置

实测数据为M=4 的Miller 码，实验中对比了M＿Viterbi、M＿XOR 和N＿Viterbi 三种算法。 由于F＿Viterbi采用FM0 解码，因此实测数据中未采用该算法。

4.3.2 性能指标

实验中，设定以下指标对算法性能进行评价。误码率定义为错误解码码元数be与总码元数bt的比值

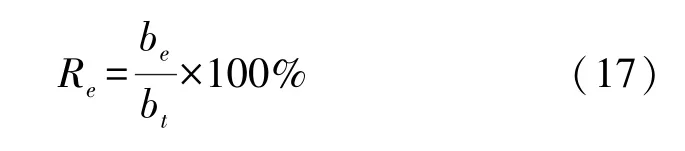
分离效率定义为成功解码标签数ns与总标签数nt的比值

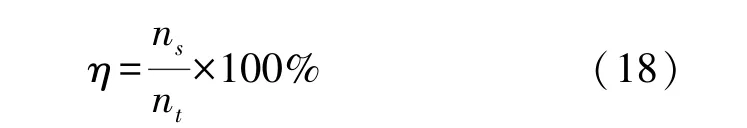
式中:只有当标签一次发送的K′个码元均被成功解码才视为该标签被成功解码。

吞吐量定义为平均一个帧中成功解码的标签数Ls与该帧长Lt的比值，表示为

以上三种指标中，越小的误码率，越高的分离效率与吞吐量值将具有越好的性能。

5 实验结果与分析

5.1 仿真数据

当信噪比取值-25 dB 到25 dB 时，图8 给出了四种算法在不同衰落系数的误码率曲线图、分离效率图及吞吐量图来比较说明各算法的性能。 衰落系数值见表2 所示，表中第1 组的衰落系数较小，第2组的系数较大。

图8(a)和图8(d)给出误码率曲线图，在信噪比为-20 dB 到5 dB 时，M＿Viterbi 算法误码率曲线始终低于F＿Viterbi 和M＿XOR 算法，信噪比在10 dB 以后，M＿Viterbi 算法无误码。 该结果说明，M＿Viterbi 算法的性能在低信噪比下，优于F＿Viterbi 和M＿XOR 算法。 同时，从M＿Viterbi 和F＿Viterbi 比较可以看出，在相同链路频率下，Miller码的性能比FM0 码更好。 另外，M＿XOR 算法在信噪比为-5 dB 到10 dB 时，误码率大幅下降，这说明当噪声变小，异或算法能使误码率得到降低，但噪声太大时传统异或的方法会产生较多的解码错误。 在图8(a)中，N＿Viterbi 算法在衰落系数很小时，在所有信噪比下均存在大量误码，而在图8(d)中，衰落系数较大时，N＿Viterbi 的误码率有一定幅度的降低，说明N＿Viterbi 算法的性能与衰落系数有关。

图8 各算法性能比较结果图

图8(b)和图8(e)分别给出不同衰落系数下的分离效率。 与误码率曲线类似，M＿Viterbi 算法分离效率曲线始终高于F＿Viterbi 和M＿XOR 算法，而N＿Viterbi的分离效率与信道衰落系数有关，信道衰落系数较低时Viterbi 算法就会发生误判，如图8(b)。图8(e)中N＿Viterbi 的分离效率随着信噪比的增大，衰落系数小于0.5 的标签始终无法正确解码，其解码性效率只能达到约50%，其原因与图4 分析的一致。

图8(c)和图8(f)给出了将各算法嵌入到ALOHA随机多址所得到的吞吐量，其中在ALOHA中帧长和标签数均设为128，当标签发生冲突时则执行冲突分离解码算法。 另外，图中还给出未采用分离型冲突分解的纯ALOHA 系统吞吐量，其吞吐量接近理论值0.367[25]。 从图中可见，当信噪比逐渐增大时，分离型冲突分解算法的吞吐量均大于纯ALOHA 系统吞吐量，M＿Viterbi、F＿Viterbi 和M＿XOR算法吞吐量最终均能达到约0.55，这说明分离型冲突分解算法确实可增大ALOHA 系统的吞吐量。图8(c)中两个标签衰落系数均很小时，N＿Viterbi算法的吞吐量与纯ALOHA 系统吞吐量相似，只能达到0.367，而图8(f)中其中一个标签衰落系数大于0.5 时能被成功分解，因此吞吐量能达到0.46。

5.2 实测数据

为了得到更可靠的实验结果，本文随机取了两组实测数据，并分别独立做了两组实验，对实验结果求均值。 实测数据分为I 路和Q 路，图9 给出了一组I 路信号，其中显示了部分前缀信号及RN16 信号，从信号图中可以看出该信号的噪声很小。 由于实测信号是Miller 编码， 因此表6 只给出了M＿Viterbi、M＿XOR 和N＿Viterbi 算法实验结果的均值。 从该表可以看到，M＿Viterbi 和M＿XOR 两种算法的误码率均为0，可见M＿Viterbi 算法在实际应用中也能达到预期的解码性能，同时，由于实测信号信噪比较小，因此M＿XOR 也没有产生误码，获得了较好的误码率性能。 N＿Viterbi 算法对信道衰落系数要求较高，即使标签数据的噪声很小该算法依然不能将标签正确解码，平均吞吐量只有0.365，与纯ALOHA 系统吞吐量理论值接近。

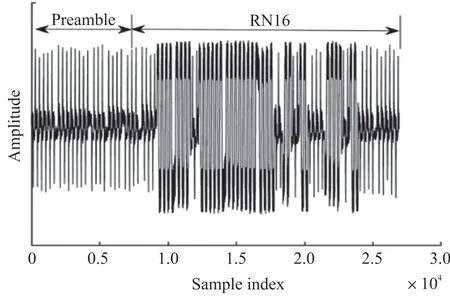
图9 实测数据的I 路信号

表6 实测数据下各算法性能

6 总结

本文针对UHF RFID 通信系统，利用物理层分离的冲突分解方法对ALOHA 随机多址中的冲突信号进行分离解码，以此提高系统的吞吐量。 在本文ALOHA 网络的仿真实验中，在10 dB 时，采用本文的M＿Viterbi 算法，系统吞吐量达到了0.55。 本文提出的M＿Viterbi 算法在与不同编码同解码算法、同编码不同解码算法以及同编码同解码而不分离标签算法的对比中，都具有5 到10 dB 的更优的解码性能。另外，本文还对实测的UHF RFID 冲突信号进行处理，实验结果表明本文算法吞吐量达到了0.55，相比传统的ALOHA 系统，吞吐量提高了约0.2。

由于无法估计3 个及3 个以上冲突标签的信道系数，因此本文算法的理论及验证实验仅完成了两个标签冲突。 由于在一个动态帧ALOHA 系统中，帧长和信号源数目可近似相等，发生3 个及3 个以上信号源冲突的概率相对较小，因此本文算法可解决该系统中较大一部分的冲突时隙。 从本文实验结果中也可以看出，分离冲突信号源为2 的冲突时隙可以进一步提高吞吐率。 另外，在本文的实测数据实验中，我们将阅读器端接收到的冲突信号数据采集提取后送至软件工具中进行处理，以得到各算法的性能指标。 更完整的测试应该是将算法嵌入至阅读器端，据此测试算法性能。 因此，在将来的工作中，我们将完成各算法应用至RFID 阅读器，从而得到更全面的实验结果。

致谢感谢电子科技大学信息与通信工程学院射频集成电路与系统研究中心提供的RFID 系统硬件设备和实验装置，并感谢研究中心的褚楚博士生帮助采集实验所需数据。