基于分数阶微分算子的集成制造系统移动设备检测数据融合技术*

左延红，左承基，袁 彬，方继根

(1.安徽建筑大学机电工程学院，安徽 合肥230601；2.合肥工业大学机械与汽车学院，安徽 合肥230009)

移动设备的质量直接影响着物流系统乃至整个集成制造系统工作的可靠性。 因此，在集成制造系统中，实时获取移动设备监测信息准确的检测数据是实现对设备的运行进行有效控制，科学地进行维修与保养，确保移动设备能正常工作的必要条件。 移动设备各部件的正确位置、运转部件的转速和温度等信息都直接关系着移动设备的工作性能。 为了实时获取移动设备工作时的准确数据，多数采用集成制造生产方式的企业应用物联网技术实现对制造装备工作信息的实时检测，但在实践中却发现:由于移动设备在生产中存在工作位置的变动性，直接限制了有线网络在移动设备检测信息传输中的应用，因此，对于物流装置检测信息的传输只得采用无线传输模式。 无线网下信息检测系统工作可靠性的主要影响因素有检测设备性能、设备工作环境、传输过程中信号干扰与能耗损失等方面，在这些影响因素的单独或共同作用下，信息检测值存在难以预测的误差。

为了提高信息检测数据的准确性，多数专家学者采用数据融合的方式实现对无线网下信息检测误差的有效处理，常见的数据融合方法有神经网络、贝叶斯估计、D-S 理论、模糊关联等[1-4]。 对于贝叶斯估计法，新概率的获取必须建立在前期先验概率的基础上，故存在应用范围的局限性[5]；D-S 证据理论能在先验概率未知的情况下对不确定性问题进行融合，利用基本概率赋值来表示不确定性问题概率的大小[6]，但该方法无法应用于高冲突证据融合。 Murphy[7]提出了一种均值证据组合规则，在证据较多时能够取得良好的融合效果，但因没有考虑到证据间的关联，证据较少时融合效果不理想；周剑等[8]提出了一种基于区间证据理论的多传感器数据融合水质判断方法，该方法可以通过寻找个别传感器异常值的方式去判断水质等级，但算法存在不能很好融合极端的数据和区间数计算量过于庞大的双重不足；王毅然[9]将两级数据融合算法应用于没鲁昂粉尘监测数据的融合处理中，但在数据的分级融合计算中使用了不同融合算法，其中需要对检测数据进行两次转换，无疑降低了数据的融合效率；刘建锋[10]提出使用互联概率加权，推导并行式和序贯式多传感器数据融合公式，实现了传感器联合概率数据在复杂环境下的融合互联，但该算法在应用过程中存在数据处理过程错综复杂，影响融合处理过程准确性的问题；田明明等学者[11]提出通过原始数据分析传感器节点的信任度，在证据融合阶段引入支持度修正证据迭代融合思想，修正传感器证据，将修正后的证据再次融合，多次迭代得到最终融合结果，完成了传感器数据融合算法，但该算法在运算中，缺乏对传感器数据在动态条件下波动情况的考虑，在应用中，精度难以保证。 本文通过对分数阶微积分理论的研究，将分数阶微分算子应用于移动设备检测信息数据的融合处理中，在提高集成制造系统移动设备监测信息数据融合处理效率和精度的同时，提高检测系统工作的可靠性。

1 分数阶微分及其应用

1.1 分数阶微分定义

分数阶微分亦称为分数阶导数，其实质就是将整数阶微分方程的微分阶次从整数扩展到分数领域。分数阶微分的理论产生于1812年，在该理论发展的几百年里，众多学者根据自己的理解方式和应用领域给出了自己的定义方法和理论体系。 因此，分数阶微分到现在还没有形成一个严格的定义，当前常用的定义有Grunwald-Letnikov(G-L)定义、Caputo 定义和Riemann-Liouville(R-L)定义三种[12]。

①分数阶微分的R-L 定义

根据柯西不定积分公式和分数阶微分与分数阶积分互为逆运算的原理，可得分数阶微分的R-L定义:

式中:0≤n-1＜v＜n，Г为Gamma 函数。

该定义的主要优点在于只需用整数阶导数就可求得它Laplace 变换的初始值，缺点在于其对函数f(x)的要求比其他定义严格，前提为函数f(x)的整数阶导数绝对可积。

②分数阶微分的G-L 定义

对于任意实数v，记v的整数部分为[v]，假设函数f(t)在区间[a，t]上有n＋1 阶连续导数，v＞0时，n≥[v]，则定义分数阶v阶导数为:

该定义是在连续函数整数阶导数经典定义的基础上，将微分的阶次由整数推广到分数，适合应用于对数值的计算。

③分数阶微分的Caputo 定义

式中:0≤n-1＜v＜n。

该定义是由于以上两种导数进行某些变换时会产生一些余项，为了实现分数阶微分计算的简单化，该定义在分数阶微积分基本性质的基础上，对Grunwald-Letnikov 定义进行了更进一步的改进。

三种定义中，由于G-L 定义存在计算过程简单、速度较高的优点而受到工程界的广泛应用，故本文采用分数阶微分的G-L 定义来研究集成制造系统移动设备检测信息数据的融合处理技术。

1.2 分数阶微分算子在检测信号处理中的幅频特性

假设在工程实践中应用物联网技术采集到一个平方可积的能量信号f(t)，且f(t)∈L2(R)，则可对信号f(t)进行Fourier 变换，得到:

根据Fourier 变换性质可知:v阶微分算子等于v阶微分乘子函数的乘性算子，将f(t)分数阶v阶导数记为fv(t)，即可得到以下方程:

从上式可以看出，能量信号的分数阶微分处理实际上就是对信号进行滤波处理，滤波函数为

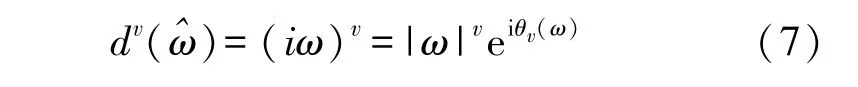
通过式(7)可以得到分数阶微分算子对检测信号处理的幅频特性，如图1 所示，根据图1 可以分析得出分数阶微分算子在能量信号的处理中，具有以下两个显著特点:①在检测信号的处理中，分数阶微分运算可以增强信号的中高频部分，提升幅度随频率和分数阶微分阶次的增加呈非线性急速增长。 因此，分数阶微分具备在提升信号中高频成分的同时非线性地保留信号中甚低频成分的作用。 ②随着分数阶次、信号频率的增大，分数阶微分算子具有显著增强能量信号中、高频部分的功能。 在信号的高频区域，不同阶次下分数阶微分算子对信号增强值间的数据差呈缩小趋势，而且同一阶次下的微分算子对不同频率下信号强度的提升效果基本相同。

图1 分数阶微分算子的幅频特性

1.3 分数阶微分融合算法的应用领域

随着近年来各国专家学者对于分数阶微积分理论的研究，发现分数阶微积分理论适合于既有非线性、非因果和非平稳等特征不正确的信号。 作为分数阶微积分理论的一份子，近年来，分数阶微分算子逐渐受到工程技术人员的高度关注，并被广泛应用于不同的应用领域，如电化学[13]、电磁场理论[14]、检测信号处理[15]、材料力学[16]等。 文献[17]将分数阶微分算子应用于煤矿井下设备信息数据的处理之中，并取得了理想的应用效果。

2 基于分数阶微分算子的移动设备检测数据融合技术

2.1 基于分数阶微分的物联网下差异性检测数据融合目标

根据分数阶微分的G-L 定义，建立基于分数阶微分的差异性检测数据融合模型:

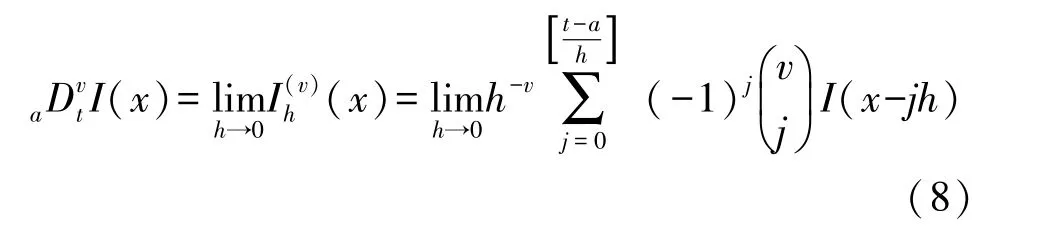
式中:0≤n-1＜n，x≥0

假设存在函数Cv(x)满足

则信号的分数阶微分可以改写为I(x)与函数Cv(x)的卷积运算为:

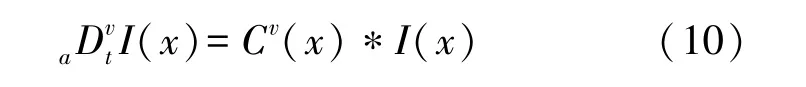
基于分数阶微分的数据融合算法其实就是应用分数阶微分算子将物联网采集的差异性检测数据进行融合处理的一种算法，实现将检测系统采集的差异性数据高精度融合。 假设应用无线网技术实时采集到某一工作区域一台移动设备的能量信息E(I)。将式(10)代入基于分数阶L2(Ω)的能量泛函，可得到基于卷积积分的分数阶变分模型:

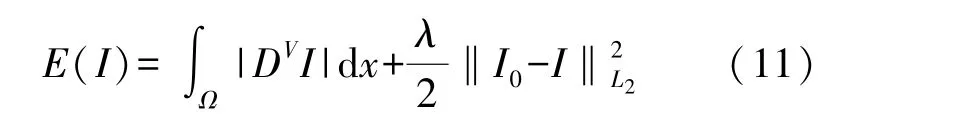
式中:I∈L2R，x∈Ω。

为了得到分数阶微分算法在式(11)下的变换解，采用基于分数阶微分算子中的极小化思想，这样就可以利用分数阶微分算法的变分法性质构造式(12)所示的差异性数据引导函数[18]:

式中:ε为任意实数，φ为任意函数。

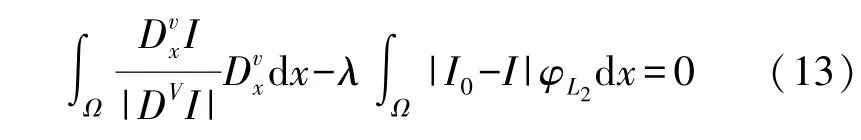
从上式可以看出，得到最终差异性数据引导模型的前提是式中的任意函数φ[19]，因此当Ω→R2时，可以得到:

根据式(11)所示的差异化数据等式可得到基于分数阶变分的物联网下差异性数据融合目标函数公式为:

根据实验设置的式(15)中相关参数，应用物联网技术采集信息数据，应用分数阶微分算法对收集到的差异性检测数据进行融合处理，再通过融合结果与式(15)间的比较，检查所用融合算法的应用效果。

2.2 基于分数阶微分的移动设备检测数据融合算法模型

由于经无线网采集到的检测数据的测量误差主要来自于仪器性能、工作环境、信号干扰和传输距离四个因素，每个影响因素均会带来信息检测数据间的差异性，现将影响因素作为影响因子x，探讨检测数据的测量值与影响因子间的函数关系式F(x)。由于标准差是反映移动设备在不同影响因素下检验检测数据质量的理想指标，因此，可将设备在不同情况下因信号失真获取的差异性检测数据间的标准差Si作为的影响因子x，根据影响因子xi与相应信息检测数据Fi可得到函数关系式为F(x)，根据式(2)可得信号F(x)基于G-L定义的v阶微分算子差异性检测数据的融合处理数学模型:

从式(16)可以看出，基于G-L 定义的分数阶微分算子对移动设备检测数据的融合过程本质上为一个多项式的计算，具备融合过程简洁的优点。 相对于D-S 证据理论和文献[5-7]中所用算法存在应用范围不全面的不足，基于分数阶微分算子的检测数据融合算法存在只需合理设置式中参数即可实现各类检测数据有效融合处理的优点；相对于文献[7]和文献[8]中所用融合算法存在公式复杂和运算量庞大带来效率低的不足，基于分数阶微分算子的检测数据融合算法具备融合速度快、效率高的优点。

2.3 基于微分算子的移动设备检测数据融合处理过程

为了有效检测集成制造系统中移动设备的监测信息，多数应用集成制造系统的制造企业先根据监测信息类型设置信息的检测误差，采用无线网络技术实时获取移动设备在生产过程中该监测信息的检测数据，再应用数据融合方法实现对信息检测数据的有效融合处理，从而提高监测信息的检测精度，分数阶微分算子对集成制造系统中移动设备监测信息检测数据的融合也不例外。 基于分数阶微分算子的集成制造系统中移动设备监测信息数据的融合处理过程分为以下7 个步骤进行。

步骤1 根据集成制造系统中移动设备的监测信息类型设置检测数据的测量误差；

步骤2 应用无线网技术实时采集集成制造系统中移动设备在生产过程中所需监测信息的检测数据Fi；

步骤3 评判检测数据Fi的测量误差，如测量误差小于系统设置误差，则检测数据无需进行融合处理，否则进入下一步；

步骤4 根据监测信息的检测数据Fi，运用MATLAB 软件拟合出检测数据测量值Fi与影响因子xi间的函数关系式F(x)；

步骤5 结合式(9)建立基于分数阶微分算子的集成制造系统中移动设备监测信息检测数据的融合处理模型；

步骤6 根据上述监测信息检测数据的融合处理模型，应用MATLAB 软件计算出各检测数据Fi的分数阶微分处理结果；

3 算法在计算机集成制造系统移动设备信息检测数据处理中的应用实验

3.1 实验平台建设

为了探索分数阶微分算子在集成制造系统移动设备信息检测数据中的融合效果，本案例采用位于合肥市经济技术开发区日立建机(中国)有限公司发动机加工车间的生产线作为实验平台。 日立建机(中国)有限公司的发动机集成制造系统中移动设备工作信息监测实验平台如图2 所示。 发动机集成制造系统的移动设备工作信息监测系统由10 台生产设备和1 台有轨物流小车(RVG)组成包括10 个作业单元、检测信息传感器、基于WIFI 的信号接收装置和中心计算机的信息检测处理单元，应用2.4 GHz WIFI 的信号传输方式实现对检测信息的传输功能。 物流小车在固定的轨道上匀速行驶10 m 才能到达下一个作业单元，在每个作业单元停留10 min 以便于各台生产设备完成自己需要完成的生产任务。

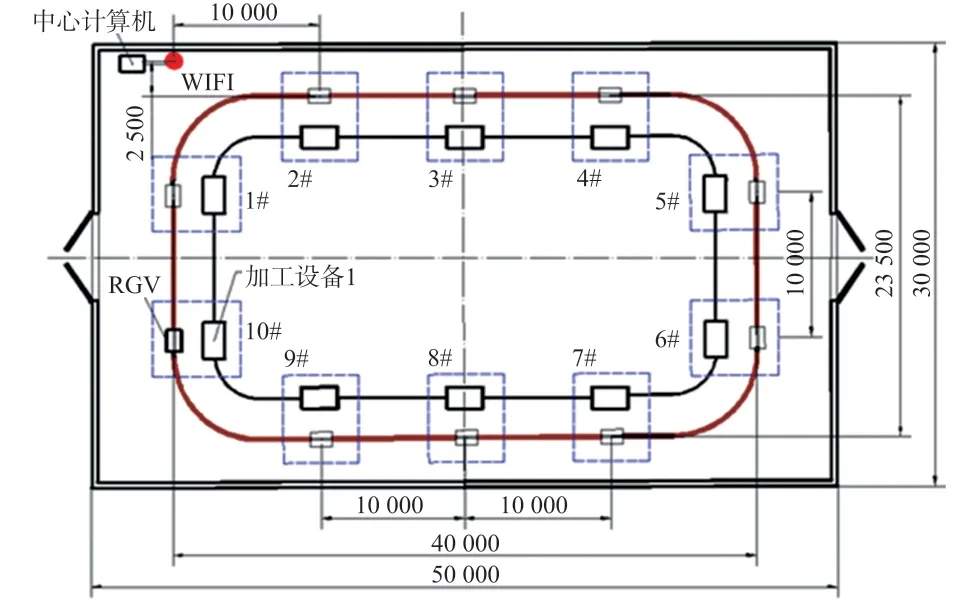
图2 集成制造系统移动设备监测信息采集系统示意图

为了不影响生产，物流小车生产信息数据的接收装置放置于车间的西北角，具体位置如图2 所示。 由于物流小车的行走机构是有轨移动设备中故障率最高部位，常见故障为因行走机构轴承的温度过高，导致轴承运转失效造成物流小车不能正常工作。 因此，本实验将发动机集成制造系统中物流小车行走机构轴承的温度作为研究对象，采用基于分数阶微分算子的检测数据融合算法对测得的信息数据进行融合处理，用来检测分数阶微分算子在集成制造系统移动设备监测信息检测数据融合处理中的应用效果。

3.2 信息检测系统对物流小车行走机构温度信息数据的采集

实验采用PT100 铂热电阻作为物流小车行走机构轴承温度的感知传感器，感知物流小车到达每个作业单元时行走机构轴承的温度，再应用基于2.4 GHz WIFI 的无线传送方式将监测信息发送至信号接收装置。 为了降低检测误差，当物流小车到达每个作业单元时在较短时间内采集5 次温度数据，采集时间间隔为5 s，剔除各单元测量误差超过5%的数据，而后取剩下检测值的平均值作为物流小车到达该作业单元时行走机构轴承温度的检测值。 根据实验，测得物流小车在到达各作业单元时行走机构轴承的温度采样值如表1 所示。

剔除表1 中的异样数据:小车在1＃作业单元时第1 次测量值14.64，小车在4＃作业单元时第3 次测量值18.36，小车在10＃作业单元时第5 次测量值20.65。 分析表2 所示数据，可知物流小车行走机构轴承在各作业单元的温度检测值与信号传输距离、作业位置、检测部位散热性能等因素有关。 从各作业单元与信息采集中心的距离和检测数据可以看出，随着信息传输距离的增加，信息的测量数据呈逐渐下降趋势；4＃作业单元与8＃作业单元与数据采集中心的距离基本相同，但由于4＃作业单元的的检测信息在传输过程中所受的干扰和削弱明显高于8＃作业单元，4＃作业单元的信息检测数据值明显小于8＃作业单元位置的数据检测值；温度检测值与检测部位散热性能有关，物流小车行走机构为了提高物流小车的承载力，使用的是采用脂润滑的滑动轴承，因此具有较好的散热性能，尽管日立建机(中国)有限公司的移动设备为进口设备，设备的散热性能好于国产设备，但物流小车位于3＃工作单元和10＃工作单元时，信息传输距离和作业环境基本相同，但受工作部位散热性能的影响，物流小车在10＃工作单元时行走轴承油温检测值明显高于3＃作业单元。与工作点及信号检测数据采集装置距离相同，设备在每个作业单元停止10 min 时间，故散热性能良好，但4＃作业单元的温度检测值依然比2＃作业单元的检测值显著增加。 如将表1 中所示数据绘制成图3 所示的物流小车行走机构轴承在各作业单元时温度分布曲线图，会发现物流小车在各作业单元时轴承油温检测值在平均值34.05 ℃上下呈无规律离散分布状态，而且测量值的标准差高达0.455 ℃。

表1 物流小车在各作业单元时轴承温度采样数据表单位:℃

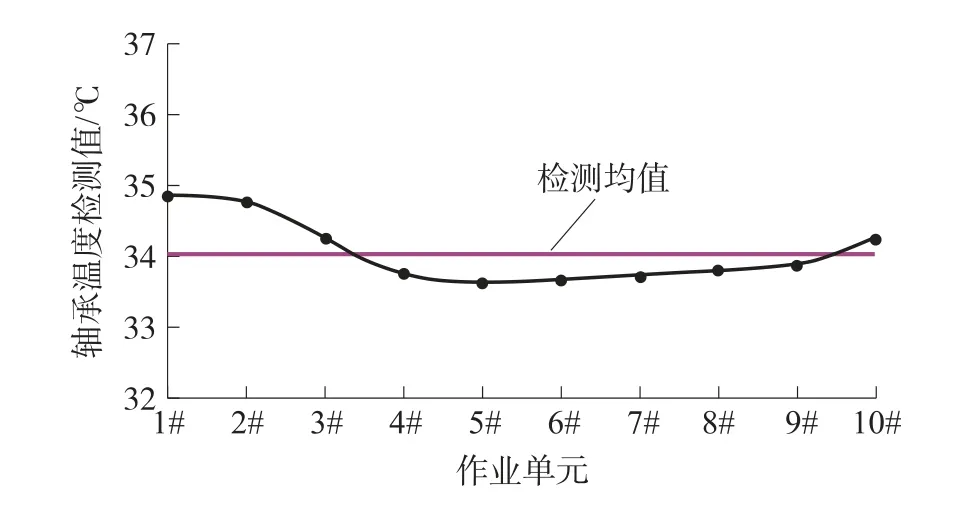
图3 RGV 行走机构轴承在各作业单元的温度分布曲线

3.3 分数阶微分算子对检测数据的融合处理

3.3.1 检测值影响因子的选择

根据上文中对于实验平台的介绍，可知整个实验均在一个车间内完成，实验时间为2 h，故环境因素对集成制造系统物流小车行走机构轴承温度检测数据间的差异性影响不大；整个实验过程中所用设备没有更换，因此设备性能对行走机构轴承温度的影响可以忽略。 由于物流小车位于不同作业单元作业时，所处工作位置的不同，会导致信号在传输过程中所受的电磁干扰强度、信号传输阻碍和传输能量损失存在较大差异性。 以上因素均是导致信号在WIFI 采集中失真的主要原因。 因此，物流小车位于不同作业单元时带来的与信号接受装置间位置的不同，是检测数据间存在较大差异性的主要原因。 如上所述，设备处于不同位置时，检测信息存在影响因素不同带来检测精度的差异性。 故本案例采用设备位于不同作业单元时的标准差作为影响因子，实现对物流小车行走机构轴承油温检测值的有效处理。

3.3.2 影响因子xi与检测值Fi间的函数关系式

最小二乘法也称为最小平方法，因在函数拟合中无需数据先验信息，且具有较好的数据拟合精度，被广泛应用于函数关系式的拟合之中，故本案例采用最小二乘法拟合影响因子xi与检测值Fi间的函数关系式F(x)。 根据表1 所示检测数据Fi和图2所示物流小车在各作业单元时与信息接受装置间的距离制定表1 所示的物流小车位于不同工作单元时轴承温度检测数据xi及其数据间的标准差，借助最小二乘法可求得物流小车在不同单元时检测数据间标准差(影响因子xi)与检测值Fi间的函数关系式F(x)，假设测量值Fi及其影响因子xi之间的函数关系式F(x)的数学表达式为:

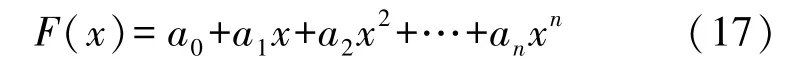
从式(17)所示的方程式可知:求出式中所示系数ai和阶次n的数值即可获得函数F(x)的关系式。 由最小二乘法的基本定义，可知式(17)所示多项式的阶次应该小于样本数，即n＜10。 应用MATLAB 软件中Polyfit 函数，可得出当多项式的阶次n=1 时，物流小车行走机构轴承的温度测量值Fi与信息传输距离xi间的总误差最小，为1.89，此时F(x)的方程式为:

3.3.3 基于分数阶微积分的检测数据融合算法模型

从式(8)可知:基于G-L 定义下的分数阶微分算子在检测数据融合中的应用，关键在于公式中阶次v和步长h运算参数的取值。

①运算参数值的选取

根据式(7)和图1 所示分数阶微分算子的幅频特性，可知当微分阶次在(0，1)区间时，信号强度在高频阶段存在随着分数阶次增加而增加的现象，但随着频率的增加，微分算子在不同阶次下对信号的增强值间的差异性呈下降趋势。 以上已在文献[20]中通过不同阶次下微分算子对差异性数据融合效果的研究得到验证。 由于本案例中频率高达2.4 GHz，故从节约篇幅和便于计算的角度出发，探讨分数阶次[0-1]之间的中间值v=0.5 时分数阶微分算子在集成制造系统移动设备监测信息检测数据融合处理中的应用效果。

结合式(8)和分数阶微分算子幅频特性，可知步长和影响因素的取值区间与信号频率相关联，但在信号的高频区域，相同阶次下的微分算子对信号增强效果间的差异性可以忽略不计，这一点亦在文献[20]中得到验证。 在分数阶次与影响因素取值区间固定不变的情况下，检测数据融合后的数值随着h值的降低略有提升，同时也带来随着融合步数n增加检测数据融合速度明显降低的不足。 因此，本案例根据分数阶微分算子频谱特性和无线网采用的工作频率，通过对表2 中所示的影响因子x(检测信息传输距离)取值区间[0.01，0.09]的分析，综合考虑融合速度和融合精度两方面因素，取融合步长h=0.01，这样需要计算的步数n=(0.09-0.01)/0.01=8。

②基于分数阶微分算子的检测数据融合算法模型

现将分数阶次v=0.5、步距h=0.01 和步数n=8代入式(8)，可得基于0.5 阶微分算子的集成制造系统物流小车行走机构轴承温度信息检测数据的融合算法模型。

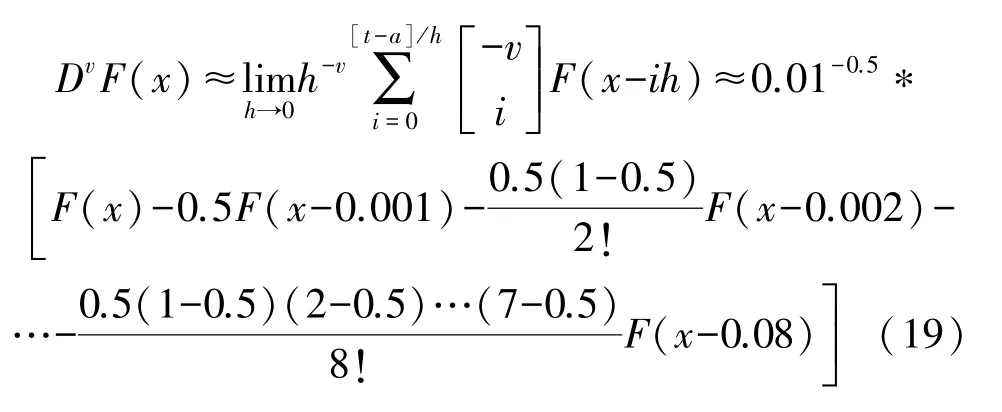
③分数阶微分对检测数据融合结果的分析

将表2 所示的影响因子xi数值代入式(11)所示的基于分数阶微分算子的物流小车行走机构轴承温度的检测数据融合处理数学模型，借助MATLAB软件即可得到表1 所示的各温度传感器在不同采样点油温检测值Fi关于影响因子xi的0.5 阶微分融合处理结果D0.5F(x)，如表2 所示。

结合表2 所示融合结果，可以看出:集成制造系统物流小车行走机构轴承温度的测量值经过0.5 阶分数阶微分算子处理后，融合数据存在以下特点:

表2 检测数据融合前后数据分析表

①分数阶微分算子具备增强检测信号在传输过程中强度的功能，融合前数据的平均值为34.05 ℃，经分0.5 阶微分算子处理后，数据的平均值为67.06 ℃，可知检测信号的增强系数高达K=1.97，有利于提高信息检测系统的工作可靠性。

②根据表2 所示数据，除以增强系数K，应用MATLAB 中Plot 函数绘制图4 所示的0.5 阶微分算子融合处理前后的数据分布图，从图4 可以看出，离散分布的检测数据经0.5 阶微分算子融合处理后，均匀地分布在平均值附近，检测数据间的差异性大幅减小，可见分数阶微分算子具有较强的差异性数据融合功能。

图4 检测数据融合前后数据分布图

③为了便于比较，现将分数阶微分算子融合后的数据除以放大系数K，可得表1 所示的物流小车行走机构轴承温度检测数据在不同融合算法下的融合精度。 经0.5 阶微分算子融合得到的数据间标准差为0.251，大幅低于平均法的0.455、最小二乘法的0.365 和文献[9]所用算法的0.528。

4 结论

移动设备是集成制造系统中的重要组成部分，但受工作方式的制约只能应用无线网技术实现对移动设备监测信息的实时在线传输，设备在不同位置时，检测信息数据受设备工作环境、信号传输距离、信号干扰和传输障碍等多种影响，带来检测数据间的差异性，直接影响着信息数据的检测精度。 针对传统融合算法在无线网移动设备监测信息数据中存在诸多不足的情况下，根据分数阶微分算子在信号处理中的应用特点，建立了基于分数阶微分算子的物联网下移动设备检测数据融合算法模型。 通过0.5 阶微分算子在集成制造系统物流小车行走机构轴承温度检测数据的融合处理实验，验证了分数阶微分算子在集成制造系统移动设备差异性检测信息的处理中，不仅具备较高的数据融合精度，还具有通过提升信号强度增强检测信号抗干扰能力和检测系统工作可靠性的双重优点。 研究成果对于提高集成制造系统中移动设备信息检测系统的工作可靠性具有重要实用价值。