融合折射学习和改进天牛须搜索的黑猩猩优化算法及其应用*

罗仕杭，何 庆

(贵州大学大数据与信息工程学院，贵州 贵阳550025)

现实世界优化问题的复杂性和难度不断增加，呈现出强约束、计算时间长、非凸性、搜索空间广等特征[1]，这使得优化问题的解决更具挑战性。 受自然界生物群体进化机制、群体社会行为规律以及自然现象规律的启发，许多元启发式优化算法相继被提出，如阿基米德优化算法(Archimedes Optimization Algorithm，AOA)[2]、被囊群算法(Tunicate Swarm Algorithm， TSA)[3]、 天 鹰 座 优 化 算 法( Aquila Optimization Algorithm，AO)[4]、哈里斯鹰算法(Harris Hawks Optimization，HHO)[5]。 由于元启发式算法无梯度机制、控制参数少且具有较高的局部最优规避能力，因此可以很好地求解这些复杂的优化问题。

黑猩猩优化算法(Chimp Optimization Algorithm)是Khishe 等人[6]于2020年提出的一种新型元启发式优化算法，其灵感来源于黑猩猩种群的等级制度和狩猎行为，用数学模型模拟黑猩猩种群通过驱赶、追逐、攻击等过程达到最优捕食的行为。 ChOA 具有原理简单、需要调节参数少、易实现等优点。 然而，与经典粒子群算法等群智能算法相似，ChOA 也存在收敛速度慢、寻优精度低和易陷入局部极值等不足，尤其对于复杂的多局部极值的高维优化问题。

为此，国内外学者对该算法进行了改进:He等[7]利用高破坏性的多项式突变初始化种群，为算法全局搜索奠定基础；Mandeep 等[8]将正余弦函数应用到黑猩猩种群的四个个体位置更新处，提高算法的收敛速度和寻优精度；Dhiman 等[9]提出了一种混合正余弦算法和斑点鬣狗算法的改进黑猩猩优化算法，改善了黑猩猩优化算法收敛速度慢和易陷入局部极值等缺陷；黄倩等[10]采用单纯形法和群个体记忆机制对较差个体进行改进，优化种群的位置更新方式，使算法的寻优性能得到提升。 上述文献对黑猩猩优化算法的改进在一定程度上提高了算法的收敛精度，降低算法陷入局部极小值的概率，但算法的寻优精度、稳定性、平衡全局搜索和局部开发能力等方面仍有待提高。

针对黑猩猩优化算法的局限性，本文提出融合折射学习和改进天牛须搜索的黑猩猩优化算法(BCRChOA)。 首先，由于天牛须搜索算法在无需确定函数具体形式和梯度信息等情况下具有高效寻优的特点，同时为了增强天牛须算法的搜索能力和搜索效率，本文利用Levy 飞行机制搜索方向和步长的不确定性将天牛须搜索的固定步长改为动态步长，提高其在搜索空间内进行深度全局探索的能力，并将其应用到黑猩猩优化算法的全局搜索阶段，有效地提升黑猩猩优化算法的搜索性能；其次，根据种群平均适应度将种群分为两个组，分别引入不同权值策略。 当个体的适应度小于种群的平均适应度，引入一个较小的惯性权值，加速算法收敛；反之，利用云模型的云滴具有随机性和稳定倾向性的特点，将云模型引入动态权值，形成云自适应动态权值，拓宽算法的搜索空间，引导种群向全局最优区域靠拢，达到平衡算法全局搜索和局部开发的能力；最后，引入基于折射定律的反向学习策略，在保持种群多样性的同时降低算法陷入局部最优的概率。

通过三类共10 个基准测试函数、部分CEC2014函数以及1 个工程优化案例进行仿真实验，实验结果表明BCRChOA 相比于标准ChOA 能在一定程度上有效地帮助算法跳出局部最优，并且提高了标准ChOA 的收敛速度、求解精度、鲁棒性等性能，同时验证其在实际工程问题中的适用性和可行性。

1 黑猩猩优化算法

ChOA 是根据自然界中黑猩猩的狩猎行为而衍生出的一种优化算法，黑猩猩根据劳动分工执行不同的行动寻找猎物。 标准的ChOA 将黑猩猩分为四种类型:攻击者、障碍者、驱赶者和追逐者，其中攻击者在狩猎过程中扮演引导种群的重要的角色，其他三类黑猩猩负责协助攻击者捕获猎物，其社会地位依次下降。

黑猩猩包围猎物的数学模型如式(1)所示:

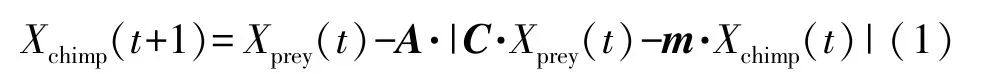
式中:Xprey为猎物的位置向量，Xchimp为当前黑猩猩个体的位置向量，t表示当前迭代次数，A、m、C为系数向量，其数学模型如式(2)～式(4)所示:

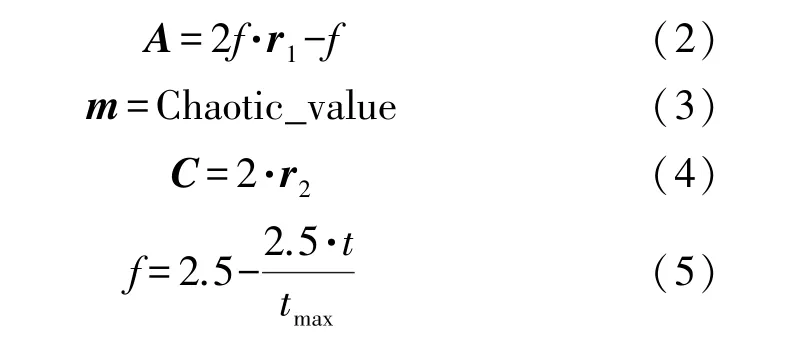
式中:r1和r2分别为取值[0，1]的随机向量；f为收敛因子，其值随迭代次数增加从2.5 线性递减到0，tmax表示最大迭代次数；A是决定黑猩猩与猎物距离的随机向量，其值为[-f，f]之间的随机数；m为混沌映射矢量，代表性动机对黑猩猩个体位置影响；C控制着猎物位置对黑猩猩个体位置的影响，其值为[0，2]之间的随机数。

黑猩猩攻击猎物的数学模型如式(6)～式(9)所示:

式中:Xattacker、Xbarrier、Xchaser、Xdriver分别表示攻击者、障碍者、追逐者和驱赶者的位置向量，X(t＋1)表示黑猩猩更新后的位置向量。

2 融合折射学习和改进天牛须搜索的黑猩猩优化算法

2.1 Levy 飞行机制改进的天牛须搜索算法

天牛须搜索算法是Jiang 等人[11]通过模拟天牛的觅食行为而提出的一种元启发式算法。 天牛使用它的两根触角感知食物气味最强烈的区域以达到觅食的目的。 天牛须搜索算法中天牛在每次迭代中头的朝向根据随机方向进行移动。 类似于天牛须搜索算法，黑猩猩优化算法中的领导者个体“攻击者”可以根据它的双耳听觉确定与猎物的距离，利用左右耳不同位置的声音判断是否更新其相对于猎物的位置。 在这个策略中，“攻击者”个体获得听觉能力，扩大对猎物的搜索范围，同时围绕最优解加强后续的种群迭代，从而提高了算法的全局搜索能力。 天牛须算法实现过程如下:

(1)对搜索方向进行标准化处理，数学模型如式(11)所示:

式中:dir 表示方向向量，random(d，1)表示生成空间维度为d的随机向量。

(2)基于“攻击者”个体的听力，探索左右区域的数学模型如式(12)所示:

式中:Xattacker(t)表示“攻击者”个体在第t次迭代的原始位置向量表示“攻击者”个体在第t次迭代向左区域搜索后的位置向量表示“攻击者”个体在第t次迭代向右区域搜索后的位置向量；η(t)表示第t次迭代黑猩猩听力感知直径。

(3)基于搜索行为和听力检测，“攻击者”个体的新位置如式(13)所示:

式中:s(t)是移动步长；f(X)是计算目标函数的适应度值；sign 函数用来确定“攻击者”个体移动后的搜索方向，若向右区域搜索适应度较大，则sign 函数取1，“攻击者”继续向右区域前进，反之，向左区域移动。 在标准天牛须搜索算法中，搜索移动s(t)一般取0.95 随迭代次数线性递减，在一次迭代过程中只搜索随机方向的某一位置，同时由式(13)可知，“攻击者”的位置和步长会随每一次迭代目标函数的变化而更新，固定步长会使得“攻击者”探索范围受到限制，不利于算法在更大范围进行探索，可能导致算法搜索能力减弱。

因此，为增强“攻击者”的搜索效率和搜索能力，本文用Levy 飞行机制的随机步长替换天牛须搜索算法中的固定步长，结合长距离跳跃和短距离游走的交替变化，不仅提高“攻击者”在广阔区域狩猎时搜索方向的多样性，而且保证了“攻击者”在最优区域进行精细搜索，极大程度地提高了算法的全局搜索能力。 图1 是步长为1000 的Levy 飞行随机游走轨迹图，如图1 所示，Levy 飞行因短距离游走和长距离跳跃相互穿梭，产生的随机步长大小和方向是不确定的，实现了对求解域的充分搜索。 将Levy飞行机制引入式(13)后，“攻击者”个体位置更新如式(14)所示:

图1 1000 步长Levy 飞行随机游走轨迹图

式中:Levy 飞行的随机步长Levy(λ)由式(15)计算:

2.2 云自适应动态权值

云模型是一个服从正态分布规律、具有稳定倾向性的随机数集，由期望值Ex、熵En、超熵He三个数字特征表示。 期望值Ex表示云滴在论域空间分布的期望，反映云滴重心位置；熵En表示定性概念的不确定性度量，用来度量定性概念的模糊度和概率，揭示模糊性和随机性的关联；超熵He是熵的不确定性度量，反映组成云模型的云滴离散程度[12]。 本文采用X-条件云生成器，输入数学期望值Ex、熵En和超熵He，则一维X-条件云滴输出如式(16)所示:

式中:E′n为服从正态分布的随机数，En为数学期望，He为标准差。

本文将云模型引入动态权值，形成云自适应动态权值，具体实现过程如下:首先，计算出所有个体适应度的平均值，然后根据每个个体的适应度值将种群分为两个子群，采用不同的权值策略分别优化两个子群。

(1)当个体适应度优于平均适应度时，则该子群为种群中较优的个体，接近当前最优解，采用较小的惯性权值ω1=0.4 加快算法的收敛速度。 将惯性权值引入“攻击者”个体位置更新处，其数学模型如式(17)所示:

(2)当个体适应度劣于平均适应度时，则这个子群为种群中较差的个体，采用基于云模型的动态权值对个体进行非线性调整。 云自适应动态权值的数学模型如式(17)～式(18)所示:

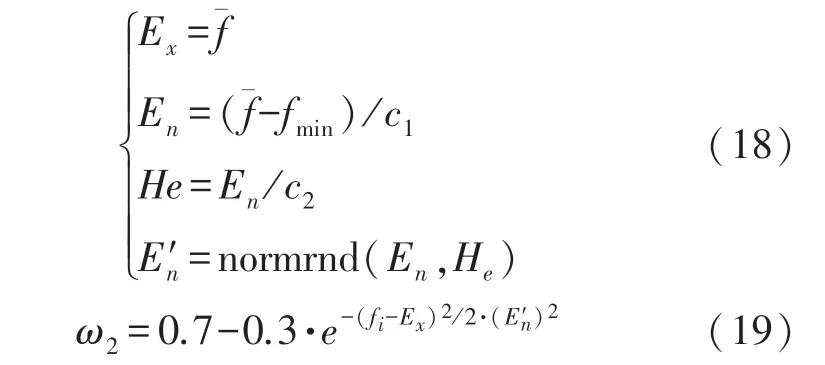
式中:c1和c2为控制参数，其值分别为3 和10；fi为种群的适应度值。 将云自适应动态权值加入“攻击者”个体位置更新处，其数学模型如式(20)所示:

在本文中，利用云模型具有随机性和稳定性倾向的特点生成云滴，然后计算云自适应动态权值。从式(20)可知，ω2的值随适应度的增加不断增大。当个体适应度较差时，不利于算法在解空间内进行覆盖性搜索，较大的动态权值具备较强的探索能力，引导算法在更广阔的区域进行搜索；反之，当个体的适应度值较好时，较小的惯性权值有助于算法专注于在已探索的区域进行精细搜索，实现算法全局勘探和局部开采能力的平衡。

2.3 基于折射定律的反向学习策略

由式(6)～式(9)可知，种群中其他黑猩猩个体位置由“攻击者”“障碍者”“驱赶者”和“追逐者”四个决策个体共同决定，当其他黑猩猩个体察觉到四个决策个体搜索到更好的猎物时会涌入到其周围的搜索区域，导致种群的多样性减少，从而使算法陷入局部最优。 为解决这一问题，本文提出一种基于折射定律的反向学习策略，计算候选解的反向解，选择较好的解继续迭代计算，增强算法的多样性，帮助算法跳出局部极值空间。

如图2 可知，O是[a，b]的中心点，全局最优个体X以O为中心点找到其对应的反向个体X′，则根据折射定律可以得出:

图2 一维空间折射反向学习示意图

设缩放因子φ=h/h′，对式(21)进行推导得到反向个体X′的数学模型，如式(22)所示:

将式(22)扩展到n维空间可得:

式中:ubj和lbj分别表示上界的第j维向量和下界的第j维向量；Xj和X′j分别表示X和X′的第j维向量。 通过对种群中最优解进行折射反向学习，将各维度值映射到解空间得到反向解，不仅避免各维度之间的干扰，而且扩大算法的搜索范围。

虽然基于折射定律的反向学习策略能够提高算法的求解精度，在很大程度上帮助算法跳出局部最优，但是无法直接判断产生的新个体位置是否优于原始个体位置。 因此，采用贪婪策略比较新旧个体适应度值，再决定是否更新个体位置，通过这种方式不断将更优解加入迭代计算，从而提升算法的寻优性能。 贪婪策略的数学模型如式(24)所示:

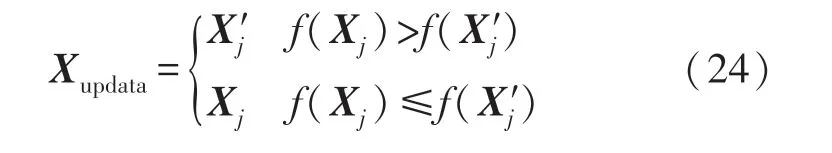
2.4 BCRChOA 算法实现步骤

综上改进策略，BCRChOA 执行步骤如下:

2.5 BCRChOA 的时间复杂度分析

BCRChOA 的时间复杂度主要由Levy 飞行机制改进的天牛须搜索算法、云自适应动态权值、基于折射定律的反向学习策略组成。 设BCRChOA 的种群规模为N，搜索空间维度为d，最大迭代次数为T，则标准BCRChOA 的时间复杂度为O(N×d×T)。

(1)Levy 飞行机制改进的天牛须搜索算法:“攻击者”个体向右区域搜索所需时间为t1，向左区域搜索所需时间为t2，产生Levy 飞行随机步长所需时间为t3，每一次按照式(14)更新“攻击者”位置所需时间为t4，所以Levy 飞行机制改进的天牛须算法的时间复杂度为O[N×d×T×t4＋(t1＋t2＋t3)]=O(N×d×T)；

(2)云自适应动态权值:采用X-条件云生成器，输入数学期望值Ex、熵En和超熵He所需时间为t5，则引入云自适应动态权值的时间复杂度为O(N×d×T＋t5)=O(N×d×T)；

(3)基于折射定律的反向学习策略:执行折射定律的反向学习所需时间为t6，利用贪婪策略比较新旧个体适应度所需时间为t7，保留最优位置时间为t8，每一维按照式(22)更新个体位置所需时间为t9，则基于折射定律的反向学习策略所需时间为O[N×d×T×(t7＋t9)＋(t6＋t8)]=O(N×d×T)。

因此，BCRChOA 的时间复杂度为O(N×d×T)＋O(N×d×T)＋O(N×d×T)=O(N×d×T)。

综上所述，BCRChOA 的时间复杂度与ChOA 一致，本文针对标准ChOA 的缺陷所提出的改进策略没有增加算法时间复杂度。

3 仿真实验与结果分析

3.1 实验设计和参数设置

仿真实验环境设置为64 位Windows 10 操作系统，CPU 为Intel(R) Core(TM) i5-7500，主频为3.4 GHz，内存为8 GB，编程软件为MATLAB R2021a。

本文挑选10 个具有不同特征的基准测试函数进行仿真实验，选取的测试函数分为三类:第一类为单模态测试函数f1～f4，用来评价算法的寻优精度和收敛速度，第二类为多模态测试函数f5～f8，用来测试算法的探索能力和跳出局部最优的能力，第三类为固定多模态测试函数f9～f10，用来评价算法的综合能力，具体信息如表1 所示。 本文选取最新的元启发式算法—天鹰座优化算法(AO)、被囊群算法(TSA)、阿基米德优化算法(AOA)、哈里斯鹰算法(HHO)以及最新改进的哈里斯鹰算法(EGHHO)[13]、黑猩猩优化算法(EChOA、SChoA、EOSMICOA)进行比较，它们的参数设置如表2 所示。

表1 基准测试函数

表2 算法参数设置

3.2 不同改进策略对ChOA 性能影响分析

为充分验证本文所提改进策略的优化效果，将标准ChOA 与本文加入Levy 飞行机制改进的天牛须搜索算法(BChOA)、添加云自适应动态权值算法(CChOA)、引入基于折射定律的反向学习策略算法(RChOA)、融合三种改进策略的改进黑猩猩优化算法(BCRChOA)，在10 个具有不同寻优特征的基准测试函数上进行30 次独立寻优，并记录30 次独立寻优的最优值、最差值、平均值和标准差。 其中，最优值和最差值反映算法单次的寻优能力，平均值体现算法运行30 次所能达到的收敛精度，标准差则体现算法的稳定性和鲁棒性。 算法参数统一设置为:种群规模N=30，搜索空间维度dim=30，最大迭代次数tmax=500。 寻优结果如表3、表4 和5 所示:

表3 的实验结果表明:对于单模态测试函数f1～f4，BCRChOA 均能寻到理论最优值，且稳定性极强。 同时BChOA 与RChOA 也能达到理论最优值，说明Levy 飞行机制改进的天牛须搜索算法可以帮助种群深度挖掘全局最优值，极大程度地提高了算法的全局搜索能力；基于折射定律的反向学习策略增强算法具有跳出局部最优的能力，提高算法的收敛精度。 仅采用云自适应动态权值策略对算法的改进有限，但是相较于标准ChOA 的寻优精度和稳定性仍然提高10 多个数量级。

表4 的实验结果表明:对于多模态测试函数f5～f8，大量局部极小值分布在其解空间中，算法进行全局寻优存在一定难度。 BCRChOA 同其他对比算法在求解函数f6时，均陷入局部极值空间，出现寻优停滞现象，但是BCRChOA 具有更高的收敛精度和稳定性。 BCRChOA 在求解其他多模态测试函数时，均可以达到理论最优值，且求解结果标准差稳定。

表5 的实验结果表明:对于固定多模态函数f9～f10，全局最优值被大量的局部最优值所包围，导致算法很难找到全局最优值。 BCRChOA 求解函数f9时，虽未寻到理论最优值，但其平均值和标准差均优于其他对比算法。 在函数f10上，BCRChOA 收敛到理论最优值，且标准差低于BChOA、CChOA 和RChOA，说明BCRChOA 具有更强的稳定性和鲁棒性。

由表3、表4 和表5 中的平均耗时可知，在函数f1～f10上，BCRChOA 的平均耗时相较于标准ChOA的算法耗时有略微降低，说明融合三种改进策略的BCRChOA 在综合寻优能力上有显著提高。 在求解函数f1～f10时，BCRChOA 的平均耗时分别要比RChOA 稍长，这是因为BCRChOA 在寻优时引入更多参数，使其在解空间中搜索到更多解，导致耗时变长，但与其他RChOA 相比差异不大，在可接受的范围内。 从综合平均耗时可以看出，本文改进算法的平均耗时比标准ChOA 短，证明本文所提三个改进策略没有增加算法的时间复杂度。

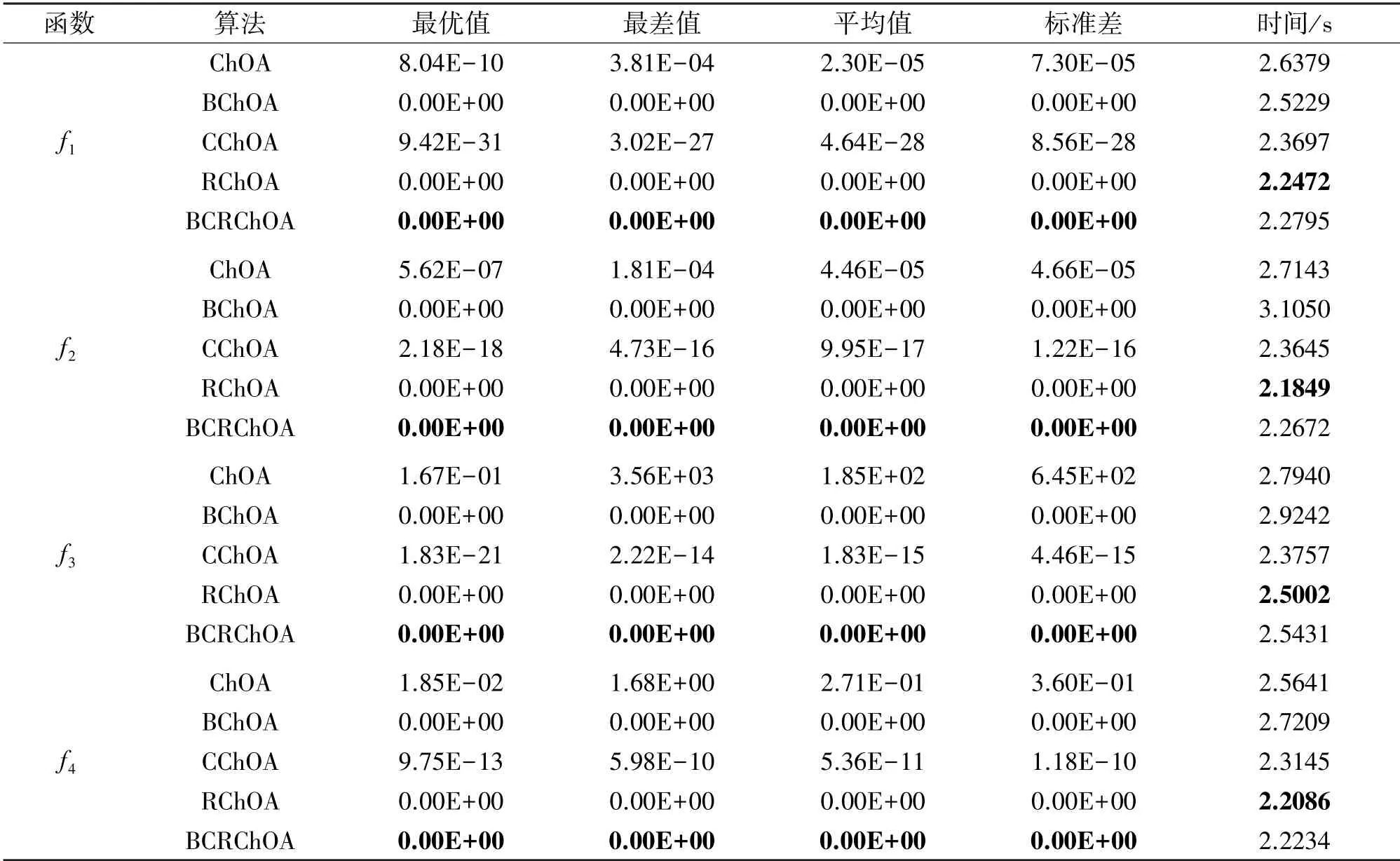
表3 不同改进策略对单模态测试函数(f1 ～f4)的优化结果对比

表4 不同改进策略对多模态测试函数(f5 ～f8)的优化结果对比

表5 不同改进策略对固定多模态测试函数(f9 ～f10)的优化结果对比

3.3 BCRChOA 收敛性分析

为了反映BCRChOA 的动态收敛特性，在搜索维度为30，独立运行30 次的条件下，纵坐标取以10为底的对数，采用平均收敛曲线图描述算法的收敛性。 图3(a)～(j)给出了10 个基准测试函数的平均收敛曲线图。

由图3 可知，在单模态测试函数和多模态测试函数上，BCRChOA 在相同的迭代次数下具有更高的寻优精度、求解效率和更快的收敛速度，表明BCRChOA在保证开拓能力的同时也能充分保证探索能力，不失种群多样性和寻优稳定性。 对于函数f6，虽然BCRChOA 与其他对比算法一样，陷入局部最优难以跳出，但是通过融合三种策略，尤其是基于折射定律的反向学习策略，可以协助算法有效地跳出局部最优，获得较高的求解精度。 总体来看，BCRChOA 的平均收敛曲线均位于4 种对比算法平均收敛曲线下方，且达到理论最优值所需的最少迭代次数。

综合表3、表4 和表5 的仿真实验结果和图3 的平均收敛曲线图，可以看出，BCRChOA 相较于对比算法具有更高的寻优精度和更快的收敛速度以及更强的稳定性，且实时性表现良好，验证了本文所提算法的有效性，达到了对标准ChOA 进行改进的目的。

图3 5 种算法的平均收敛曲线图

3.4 BCRChOA 与最新元启发式算法及其改进算法对比分析

为进一步验证BCRChOA 的有效性和优越性，本文将BCRChOA 与天鹰座优化算法(AO)、被囊群算法(TSA)、阿基米德优化算法(AOA)、哈里斯鹰算法(HHO)以及最新改进的哈里斯鹰算法(EGHHO)、三种改进黑猩猩优化算法(EOSMICOA、SChoA、EChOA)进行对比，其中EChOA、SChoA、EOSMICOA、EGHHO的数据分别来源于文献[7，8，10，13]，采用与所选文献相同的实验参数设置(种群规模N=30，最大迭代次数tmax=500)，对于每个基准测试函数的搜索维度分别设置为30/500/1000，各算法独立运行30 次，将平均值和标准差作为评价指标，结果如表6、表7 和8所示(“—”为缺失数据)。

由表6 和表7 可知，无论是求解单模态测试函数还是多模态测试函数函数，BCRChOA 的寻优精度和鲁棒性是9 种算法中最好的，尤其是对于函数f2、f4和f8，8 种对比算法求解精度低或无法求解时，BCRChOA 求解效果达到100%，可以寻到理论最优值。

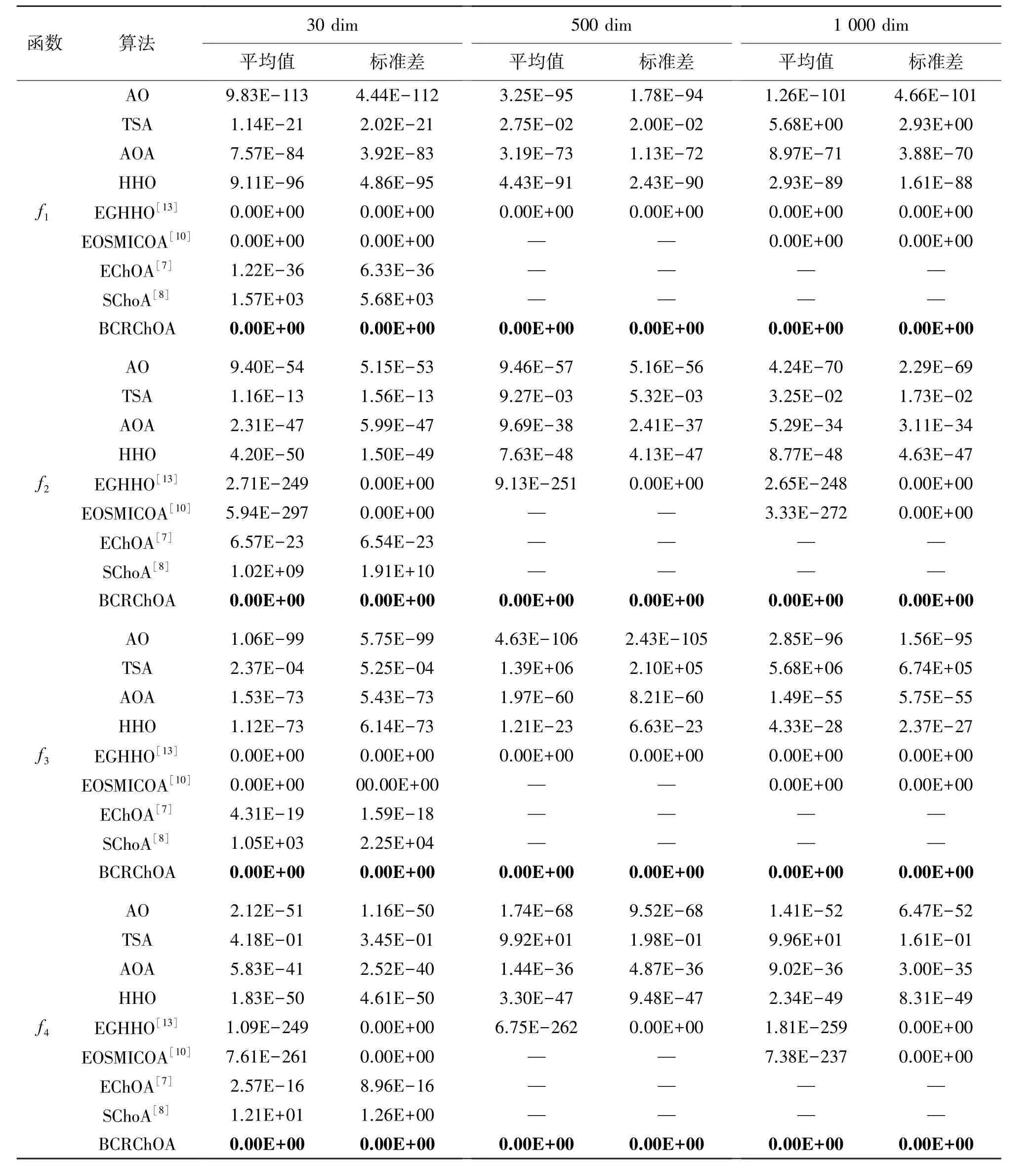
表6 9 种算法对单模态测试函数优化结果比较

表7 9 种算法对多模态测试函数优化结果比较

由表8 可知，对于固定多模态测试函数f9～f10，BCRChOA 的求解结果非常接近或等于理论最优值。 当搜索空间维度从30 维上升到500 维再上升到1000 维时，寻优过程需要更多计算，导致算法的搜索精度和稳定性均有不同程度下降，但是相较于8 种对比算法，BCRChOA 仍具有最高寻优精度。 因此，BCRChOA 在求解低维和高维问题时，寻优性能和稳定性相对更好，进一步佐证了BCRChOA 在解决高维复杂的优化问题时具有显著的竞争优势。

表8 9 种算法对固定多模态测试函数优化结果比较

3.5 BCRChOA 对CEC2014 测试函数寻优性能分析

为了更进一步验证BCRChOA 解决具有复杂特征的问题时的有效性和鲁棒性，本文将BCRChOA应用于优化部分CEC2014 测试函数，所选取的函数类型包括单峰函数、多峰函数、混合和复杂的合成函数，其详细信息如表9 所示。 本文选用BCRChOA与ChOA、HHO 算法、AO 算法、TSA、AOA 算法优化9 个CEC2014 测试函数。 实验参数设置空间维度为30，最大迭代次数为1000，每个算法分别独立运行30 次，优化结果如表10 所示。

表9 部分CEC2014 函数介绍

表10 不同算法对CEC2014 测试函数优化结果比较

由表10 可知，在单峰函数CEC03 上，AOA 表现最好，而BCRChOA 求解精度低于标准AOA，这是因为Levy 飞行机制改进的天牛搜索算法需要进行更多的参数计算，造成寻优精度有所下降。 对于多峰函数CEC06、CEC12，BCRChOA 寻优性能排名第一，同时在CEC16 上，BCRChOA 与HHO 算法、AO 算法、TSA、AOA 求解精度并列第一，但是BCRChOA具有更小的标准差，说明其稳定性更好。 对于混合函数CEC19，BCRChOA 寻优精度更加接近理论最优值。 在复杂的合成函数CEC23、CEC24 和CEC25上，BCRChOA 的标准差为0，说明其求解复合特征函数时具有极强的稳定性和鲁棒性。 综上寻优结果分析表明，BCRChOA 在解决具有复杂特征的问题时具有明显竞争优势。

4 BCRChOA 在工程优化问题中的应用

工程优化问题是在科学和工程应用领域中常见的约束优化问题。 本文将所提的新型元启发式优化算法BCRChOA 用于优化工程设计问题，进一步验证所提算法的可行性和适用性。 约束优化问题的数学模型描述如式(25)所示[14]:

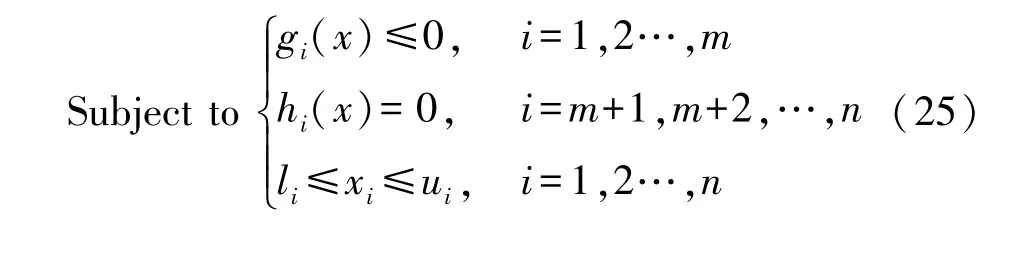
式中:f(x)为目标函数，x为决策变量，x=(x1，x2，x3…xn)∈Rn，g1，g2，…，gm和hm＋1，hm＋2，…，hn是域中的实值函数。

约束条件的处理是求解约束优化问题的关键。在实际工程优化问题中，最常见的方法是在目标函数上添加一个“惩罚项”，将约束定义为一个整体，其满足约束而不影响解，从而将约束问题转换为无约束的优化问题[15]。 惩罚函数的数学模型如式(26)所示:

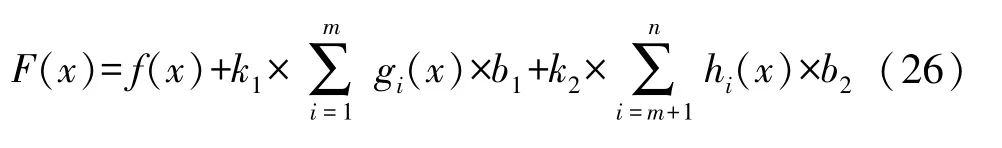
式中:f(x)为目标函数，不等式惩罚系数为k1，等式惩罚系数为k2，gi(x)是不等式约束，hi(x)是等式约束，b1和b2的定义如式(27)所示:

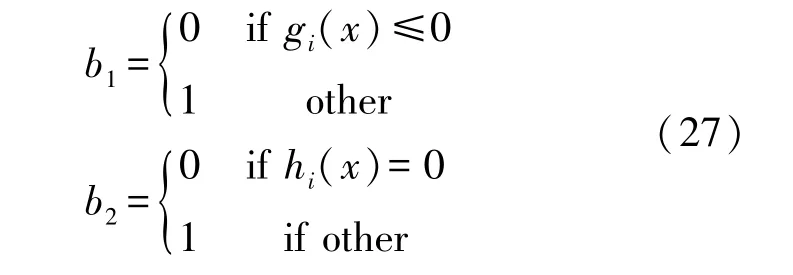
4.1 工程优化设计仿真实验参数设置

本文利用BCRChOA 优化减速器设计。 仿真实验将BCRChOA 与ChOA、引力搜索算法(Gravitational Search Algorithm，GSA)[16]、正余弦算法(Sine Cosine Algorithm，SCA)[17]、HHO 算法、AO 算法、TSA、粒子群算法(Particle Swarm Optimization，PSO)[18]、樽海鞘群算法(Salp Swarm Algorithm，SSA)[19]、鲸鱼优化算法(Whale Optimization Algorithm，WOA)[20]、灰狼优化算法(Grey Wolf Optimizer，GWO)[21]、帝王企鹅优化算法(Emperor Penguin Optimizer，EPO)[22]、多元宇宙优化算法(Multi-Verse Optimizer，MVO)[23]、斑鬣狗优化算法(Spotted Hyena Optimizer，SHO)[24]、混合萤火虫粒子群算法(Hybrid Firefly and Particle Swarm Optimization Algorithm，HFPSO)[25]、改进的黑猩猩优化算法(Enhanced Chimp Optimization Algorithm，EChOA)、AOA、均衡优化算法(Equilibrium Optimizer，EO)[26]进行实验对比。 为了保证实验的公平性，选取与文献测试参数一致，设置种群大小为50，最大迭代次数为1000，每个算法独立运行30 次后取平均值。

4.2 减速器设计问题

减速器设计是在7 个决策变量和11 个约束条件下，以找到减速器的最小重量为优化目标。 决策变量分别为面宽(b)、齿轮模数(m)、小齿轮上的齿数(p)、轴承之间第一轴的长度(l1)、轴承之间第二轴的长度(l2)、第一轴直径(d1)、第二轴的直径(d2)，其结构设计示意如图4 所示。

图4 减速器设计示意图

减速器设计的数学模型如下:

根据表11 给出的BCRChOA 与其他算法优化减速器设计的结果，BCRChOA 获得的最优解为[b，m，p，l1，l2，d1，d2] =[3.192，0.700，17.000，7.300，7.666，3.538，5.317]，最优值f(z)= 2982.921，表明BCRChOA 能在最小化减速器重量上获得最佳解决方案，其有效性优于其他对比算法。 通过减速器设计实例进一步佐证BCRChOA 在实际工程问题中的可行性和适用性。

表11 不同算法求解减速器设计问题的优化结果对比

5 结论

为改善标准ChOA 存在全局搜索能力弱、收敛精度低、易陷入局部最优等不足，本文在黑猩猩优化算法的全局搜索阶段采用Levy 飞机机制改进的天牛须搜索算法，利用天牛须搜索算法具有较强的搜索能力和Levy 飞行机制随机步长搜索大小和方向的不确定性来增强黑猩猩种群搜索的多元性，进而提高算法的全局探索能力；其次，采用云自适应动态权值平衡算法全局探索和局部开发能力；最后，将基于折射定律的反向学习策略生成的反向解应用到当前最优解，对种群在局部阶段聚集程度进行分析，生成的动态解不仅增强算法的多样性，而且协助算法跳出局部最优。 通过10 个基准测试函数、部分CEC2014 测试函数验证了BCRChOA 的寻优精度、收敛速度和鲁棒性均较对比算法有显著提升，同时通过减速器设计工程案例优化问题进一步验证BCRChOA 在实际应用中的可行性和适用性，为解决复杂约束问题提供一条有效途径。 下一步研究工作是将BCRChOA 用于求解多目标优化问题。