传动间隙引起的电动舵机自振荡现象研究

刘 鹏，李怀兵，杨超凡，陈 婷，刘 凯

(北京精密机电控制设备研究所，北京 100076)

0 引 言

为了保证润滑或者为了避免变形卡滞，传动间隙是机械传递过程正常进行不可避免的一种非线性。间隙的存在增加了传动系统控制的复杂程度，会引起系统的自振荡，使系统动态性能降低，因而在运行精度要求较高的伺服系统领域，间隙非线性一致都是研究的重要内容之一[1]。

在工程实践中经常遇到一些现象，例如对于一些带宽要求较高的伺服系统，一般增益值较大，舵机在零位时经常会有杂声，查看位置传感器反馈信号会发现反馈信号呈小幅度周期振荡，当降低增益值或者更换传动组件后，振荡现象就会消失。从工程经验来讲上述问题应该是由传动间隙引起的。本文的目标就是从机理上解释间隙引起的电动舵机自振荡现象产生的原因，分析该自振荡频率和幅值的影响因素，以及不同控制策略对该自振荡的影响。力求在机理上解释和解决实际工程问题。

1 传动间隙数学模型的建立和非线性系统的研究方法

1.1 传动间隙数学模型的建立

图1为典型的电动舵机结构图。其运动传动过程为电机转动通过齿轮副传递给滚珠丝杠副，丝杠螺母上安装有线位移传感器，将位置信号反馈给控制器，形成闭环控制。

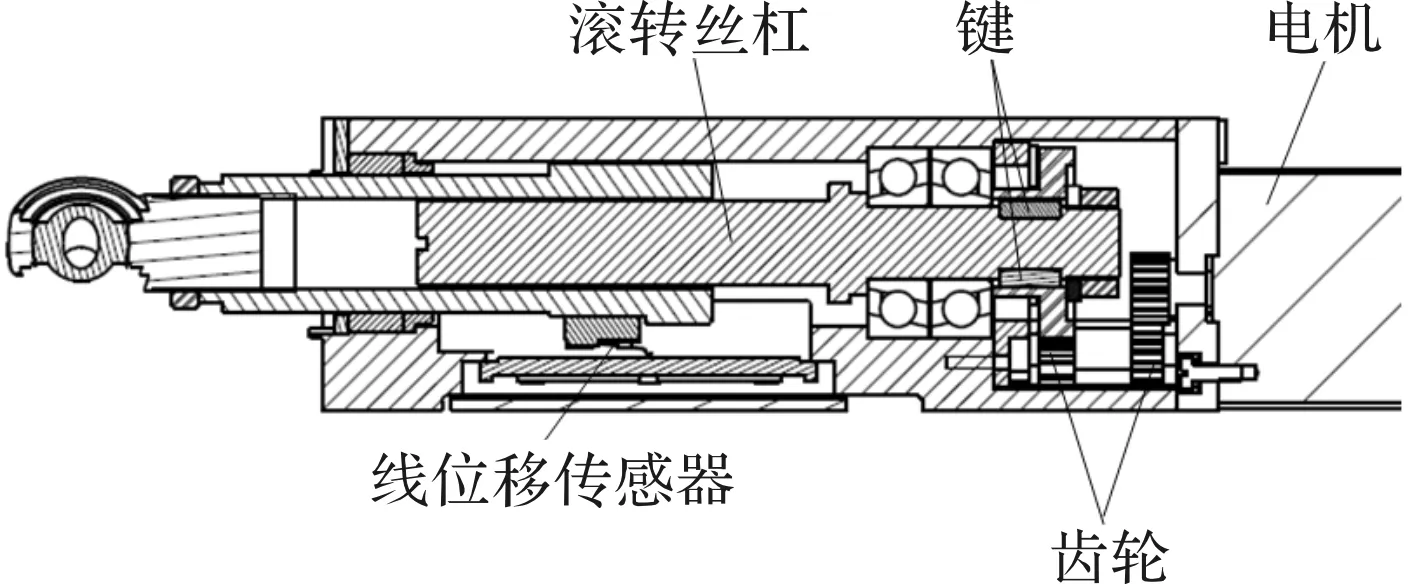
图1 电动舵机结构图

电机一般通过圆柱销或者平键与主动齿轮连接，从动齿轮一般通过平键与滚珠丝杠连接，圆柱销一般为过盈配合，平键一般采用双键，可有效消除间隙。并且滚珠丝杠副一般通过增大钢球来消除间隙。所以在电动舵机内部传动间隙主要存在于齿轮副中。

电动舵机的工作状态分空载状态和带载状态，空载状态是指可忽略主动齿轮之后的所有负载和转动惯量的情况，当电动舵机摆放在桌面上工作，或者装舱后被驱动的舵片很小时，均可认为属于空载状态。不同的带载状态传动间隙的运动和受力行为也有所不同，需不同的数学模型来描述。空载状态下，传动间隙一般用迟滞模型描述，带载状态下，传动间隙一般用死区模型描述[2-4]。由于空载状态下电动舵机稳定性分析是电动舵机稳定性分析的前提和基础，因此本文重点运用传动间隙的迟滞模型分析空载状态下齿轮传动间隙引起的电动舵机自振荡现象。

迟滞模型的函数曲线如图2所示。

图2 迟滞模型函数曲线

数学表达式为

以齿轮副间隙为例对上式进行解释，x表示输入齿轮转角，y表示输出齿轮转角，k0表示传动减速比，b表示单边间隙值(总间隙值为2b)，a表示主动轮换向时主动轮所处的角度值。迟滞模型实质为一个运动学模型，其对于描述空载状态下电动舵机的传动间隙是比较适合的。

1.2 描述函数法

本文采用描述函数法对含传动间隙的非线性系统进行研究。描述函数法是基于频率分析法和非线性特性谐波线性化的一种图解分析方法。该方法对于满足结构要求的一类非线性系统通过谐波线性化，将非线性特性近似表示为复变增益环节，然后推广应用频率法，分析非线性系统的稳定性或自激振荡[5]。

运用描述函数法时，非线性系统应简化成一个非线性环节和一个线性部分连接的典型结构形式，如图3所示。

图3 描述函数法应用的典型结构形式

当非线性特性采用描述函数近似等效时，闭环系统的特征方程为1+N(A)G(jω)=0，即为G(jω)=-1/N(A)，称-1/N(A)为非线性环节的负倒数描述函数。若线性部分奈奎斯特曲线包围曲线-1/N(A)，系统不稳定；若线性部分奈奎斯特曲线不包围曲线-1/N(A)，系统稳定；若线性部分奈奎斯特曲线与曲线-1/N(A)有交点，则系统存在着无外作用下的周期运动，即自振荡。

减速比为1时，迟滞模型的描述函数为

式中，b为单边间隙值，A为输入信号幅值。

2 传动间隙引起的自振荡受控制算法的影响情况

在实际工程中，小功率电动舵机通常使用有刷或无刷直流伺服电机，在控制中只有单独的位置闭环回路。

不考虑系统中除传动间隙外的其它非线性，建立在空载状态下，单环控制电动舵机的结构图，如图4所示，该模型为最基础的电动舵机系统模型。

图4 空载下单环控制电动舵机系统结构图

通过对结构图的等效化简，得到化简后的空载状态下单环控制电动舵机的结构图，如图5所示。

图5 等效化简后系统结构图

2.1 比例控制

采用比例控制时，根据图5可得系统系统线性部分的开环传递函数如下：

某电动舵机的参数定义如下：

R=0.105 Ω——电机等效电阻

L=0.00045 H——电机等效电感

Cm=0.008 N.m/A——电机力矩系数

Ce=0.105 V.s/rad——反电动势系数

fd=3×10-3——电机粘性力矩系数

Jd=6.2×10-5kg.m2——电机的转动惯量

P=1——比例系数

U=160 V——供电电压

i齿轮=2.8——齿轮的减速比

i丝杠=1570 rad/m——丝杠的减速比

k线角=1014.5°/m——作动杆伸出长度转化为舵轴转角的转化关系

将数据代入公式，可得

系统开环对数频率特性曲线(bode图)如图6所示，系统开环幅相特性曲线如图7所示。从图中可以看出系统起点A(0)=∞,φ(0)=-90°，终点A(∞)=0,φ(∞)=-270°，与实轴有一个交点，不包围(-1，j0)点，系统稳定。

图6 系统线性部分开环对数频率特性曲线

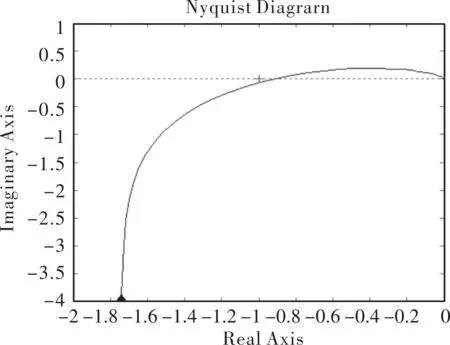
图7 系统线性部分开环幅相曲线

迟滞模型的单边间隙值取为0.5°(0.00872 rad),将-1/N(A)曲线叠加到系统线性部分开环幅相曲线上，如图8所示。-1/N(A)曲线起点为(-∞，-∞j)，终点为(-1,j0)。从图中可以看出开环幅相曲线与-1/N(A)曲线有点1和点2两个交点，-1/N(A)曲线方向为从左指向右。系统中存在两个周期运动，点1的幅值记为A10，点2的幅值记为A20。外界扰动使非线性环节输入幅值为A，当AA20时，系统稳定，振幅将衰减，最终也将回到A20点。点2对应着一个稳定的周期运动，在相平面法中称为极限环振荡，本文称为自振荡。

图8 系统线性部分开环幅相曲线与-1/N(A)曲线相对位置

从图8可以直接读出在点2处的频率w=171 rad/s(T=0.0367 s)，-1/N(A)=-1.21-0.304j，从描述函数中可以解出A=0.04583 rad。

按图4仿真模型进行仿真，系统输入指令为0。使间隙环节前的积分环节初始条件(即间隙环节的输入扰动)为0.5 rad，通过仿真，间隙环节会输出一个稳定的振动如图9所示。间隙环节的输出经过传递环节后，可在位置传感器上读出，如图10所示。从图解法及仿真结果可以看出，传动间隙引起电动舵机产生自振荡的条件为线性部分开环幅相曲线局部包围非线性环节的负倒数描述函数-1/N(A)。

图9 间隙环节输入输出曲线

图10 位置传感器输出信号

当比例系数发生变化时，线性部分的开环幅相特性曲线也会发生变化比例系数分别取P=1，0.8，0.5时，开环对数频率特性曲线如图11所示，从图中可以看出比例系数变化时，相位特性不变，幅值特性改变。从图12开环幅相特性曲线可以看出随着比例系数的减小，开环幅相特性曲线曲线会右移。当曲线与-1/N(A)无交点时，则系统一直稳定，不会产生自振荡。

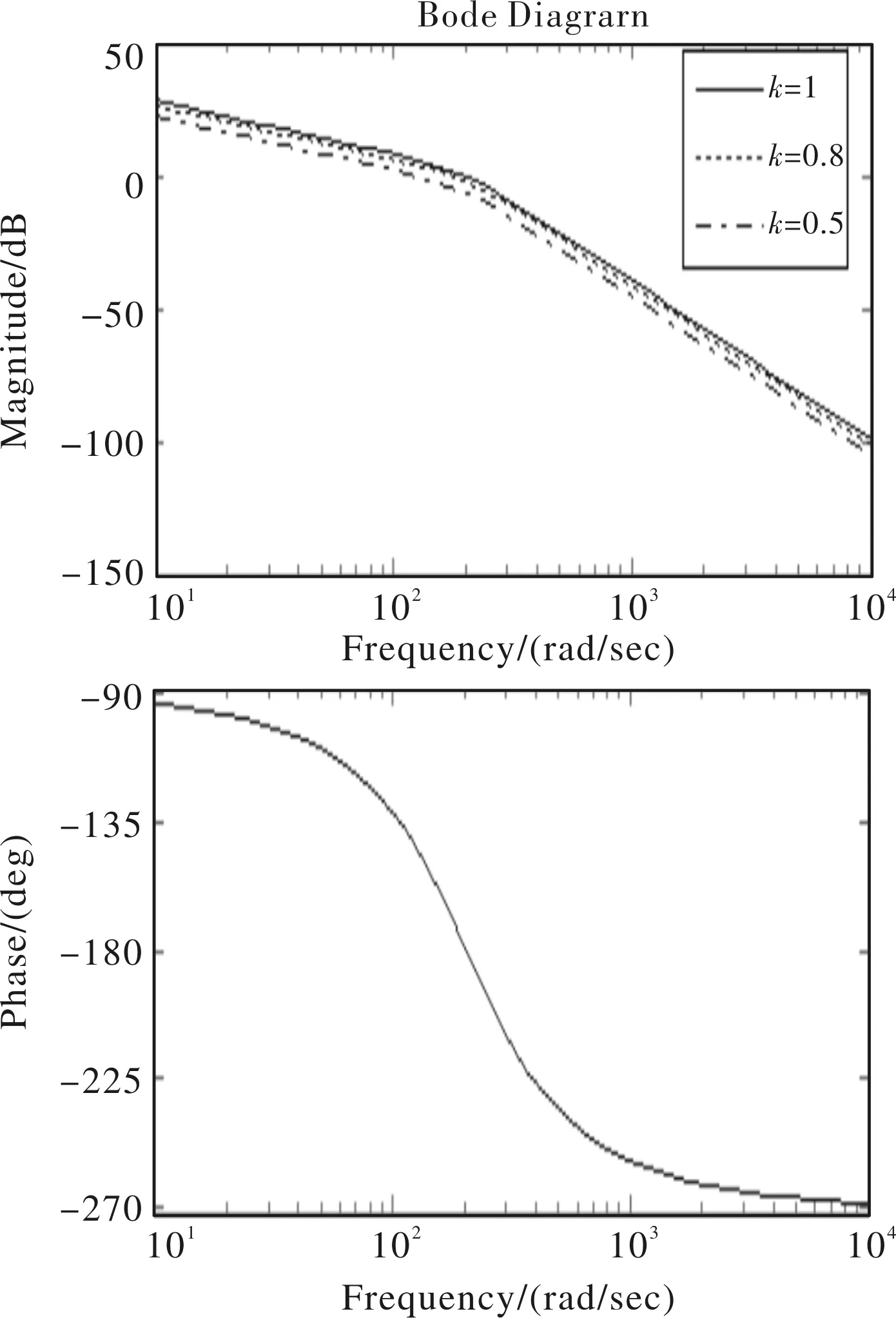
图11 比例变化时系统线性部分开环对数频率特性曲线

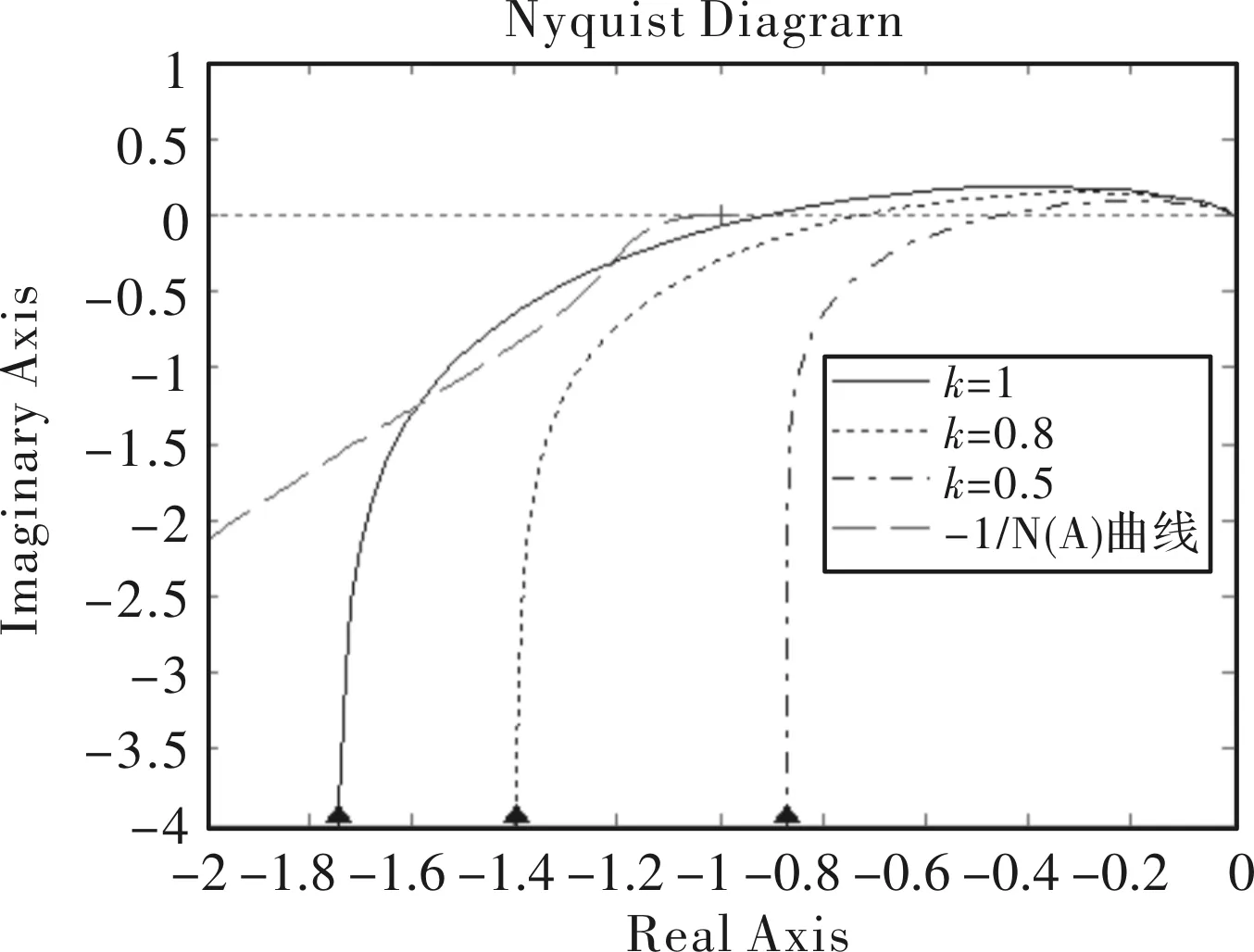
图12 比例变化时系统线性部分开环幅相曲线

2.2 比例微分控制

系统采用比例加微分控制时，比例微分环节的传递函数为P(1+Kds)，系统线性部分的开环传递函数。与比例控制相比，比例微分控制增加了一个一阶微分环节。取比例系数P=1，微分系数Kd=0.01,其它参数按上一节取值，可得系统线性部分开环幅相曲线，如图13所示 。从图中可以看出，增加微分后，系统线性部分开环幅相曲线向第四象限偏移，不易与-1/N(A)曲线相交，也就不易形成自振荡。

图13 增加微分后系统线性部分开环幅相曲线

2.3 比例积分分控制

系统采用比例加积分控制时，比例积分环节的传递函数为P(1+KI/s)，与比例控制相比，比例积分将系统型别由Ⅰ型变为Ⅱ型，并且增加了一个一阶微分环节。取比例系数P=1，积分系数KI=1，其它参数按2.1节取值，可得系统线性部分开环幅相曲线，如图14所示。从图中可以看出，增加积分后，系统线性部分开环幅相曲线向第三象限偏移，更易与-1/N(A)曲线相交，也就容易形成自振荡。

图14 增加积分后系统线性部分开环幅相曲线

3 传动间隙引起的自振荡频率和幅值的影响因素

通过前文分析可知，间隙引起的自振荡频率和幅值取决于系统线性部分开环幅相曲线与-1/N(A)曲线的交点。自振荡频率由线性部分决定，振荡幅值通过交点和描述函数公式求解得到。

从式1可以看出改变单边间隙值b的大小时，-1/N(A)曲线不会发生变化，这是因为在公式中可以看出虽然A是自变量，但是完全可以将b/A看成一个自变量，这样描述函数曲线就与b的取值无关。当b变化时，线性部分开环幅相曲线和-1/N(A)的交点(Re(-1/N(A)),Im(-1/N(A)))不变，但是根据交点求得的A的值会发生变化，即间隙值b不影响自振荡的频率，但会影响自振荡的幅值。图15为不同间隙下自振荡幅值A与交点虚部的函数曲线。从图中可以看出，交点虚部取相同值时，间隙值越大，求得的自振荡幅值也越大。

图15 幅值A的函数曲线

4 实例分析

如图16所示，为某电动舵机在零指令下发生了自振荡现象，图中为位置传感器输出信号。可以看出曲线在-0.020°～+0.020°之间波动变化(周期16 s左右)。

图16 幅值A的函数曲线

按照上文分析，建立系统模型，调整线性部分调节线性部分参数，使系统开环幅相曲线与-1/N(A)曲线交点频率为0.3925 rad/s左右。调节间隙值可以使位置传感器输出幅值为0.02°。如图17所示，仿真结果可与实际情况一致。

图17 仿真结果

5 结 论

通过本文分析可得到以下结论：

(1)空载状态下，纯比例控制时，通过减小比例系数可以避免间隙引起的自振荡。

(2)在比例控制的基础上适当地增加微分控制有利于避免间隙引起的自振荡。

(3)在比例控制的基础上增加积分控制易于产生间隙引起的自振荡。

(4)间隙引起电动舵机的自振荡频率由线性部分决定，与间隙值的大小无关，间隙值会影响振荡的幅值，间隙值越大，自振荡幅值也越大。