处于混沌状态的IPMSM位置控制方法研究
张 峰,黄 欣,白雪莲,王鹏飞,黄 玉
(陆军炮兵防空兵学院 电气工程教研室,合肥 230031)
0 引 言
混沌运动是非线性动力学系统所特有的一种运动形式,广泛存在于自然界中。一般而言,混沌是指在确定性的非线性系统中,不需要附加任何随机因素就可以出现的类似随机的行为。自1963年Lorenz在三维自治系统中发现了第一个混沌吸引子以来,人们就对混沌系统开展了广泛的研究[1-2]。
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有运行可靠、效率和功率密度高等优点,在工业生产、电动汽车、机器人等领域得到了广泛的应用[3-6]。PMSM是一个非线性、强耦合的系统,也有可能处于混沌状态。Li等[7]基于d-q坐标系下的模型研究了气隙均匀的表贴式永磁同步电机(SPMSM)的混沌特性。Jing等[8]进一步讨论了气隙非均匀的内置式永磁同步电机(IPMSM)的情况。其他一些研究[9-12]也在文献[7]的基础上进一步展开。但以上这些研究[7-12]都对PMSM中的参数约束关系进行了一定程度的放松。Zhang等[13]在更加严格的遵循模型中参数约束关系的条件下发现考虑扭转弹性转矩时IPMSM系统在一定的参数条件下可以处于混沌状态或超混沌状态。但文献[13]只对IPMSM模型本体进行了研究,没有考虑对其进行控制的问题。另一方面,由于文献[7]不考虑扭转弹性转矩的作用,此时电机可以处于匀速转动的稳定状态,所以目前基于文献[7]开展的电机控制研究主要针对的是电机的速度控制问题[12]。文献[13]考虑了扭转弹性转矩的作用,此时匀速转动不再是系统的稳定状态[13],因此本文对扭转弹性转矩作用下处于混沌状态的IPMSM的位置(转角)控制方法进行了研究。
本文首先给出了d-q坐标系下考虑扭转弹性转矩时IPMSM的系统模型及其处于某一混沌状态时的Lyapunov指数、状态变量时序图和状态空间相图。然后采用基于PI的交流电机三环(位置环、速度环、电流环)矢量控制[3-4]方法对扭转弹性转矩作用下处于混沌状态的IPMSM设计了位置控制系统,其中位置环采用了依据位置给定值与位置实际值的差值大小改变PI控制系数的策略,电流环采用了最大转矩电流比(MTPA)[4]控制策略。接下来,在位置环引入了一种基于趋近率的滑模鲁棒控制[5-6,14],并采用了依据位置给定值与位置实际值的差值大小改变滑模控制器系数的策略。针对引入滑模控制后,电流环控制中MTPA控制策略不便于使用,而d轴电流等于零(id=0)控制策略又不能发挥IPMSM优势,会导致控制收敛速度变慢的问题,采用了将d轴电流的给定设置为某一适当负值的控制策略。最后,通过仿真实验对以上两种控制方案进行了验证和对比。
1 考虑扭转弹性转矩时IPMSM的系统模型及其混沌状态
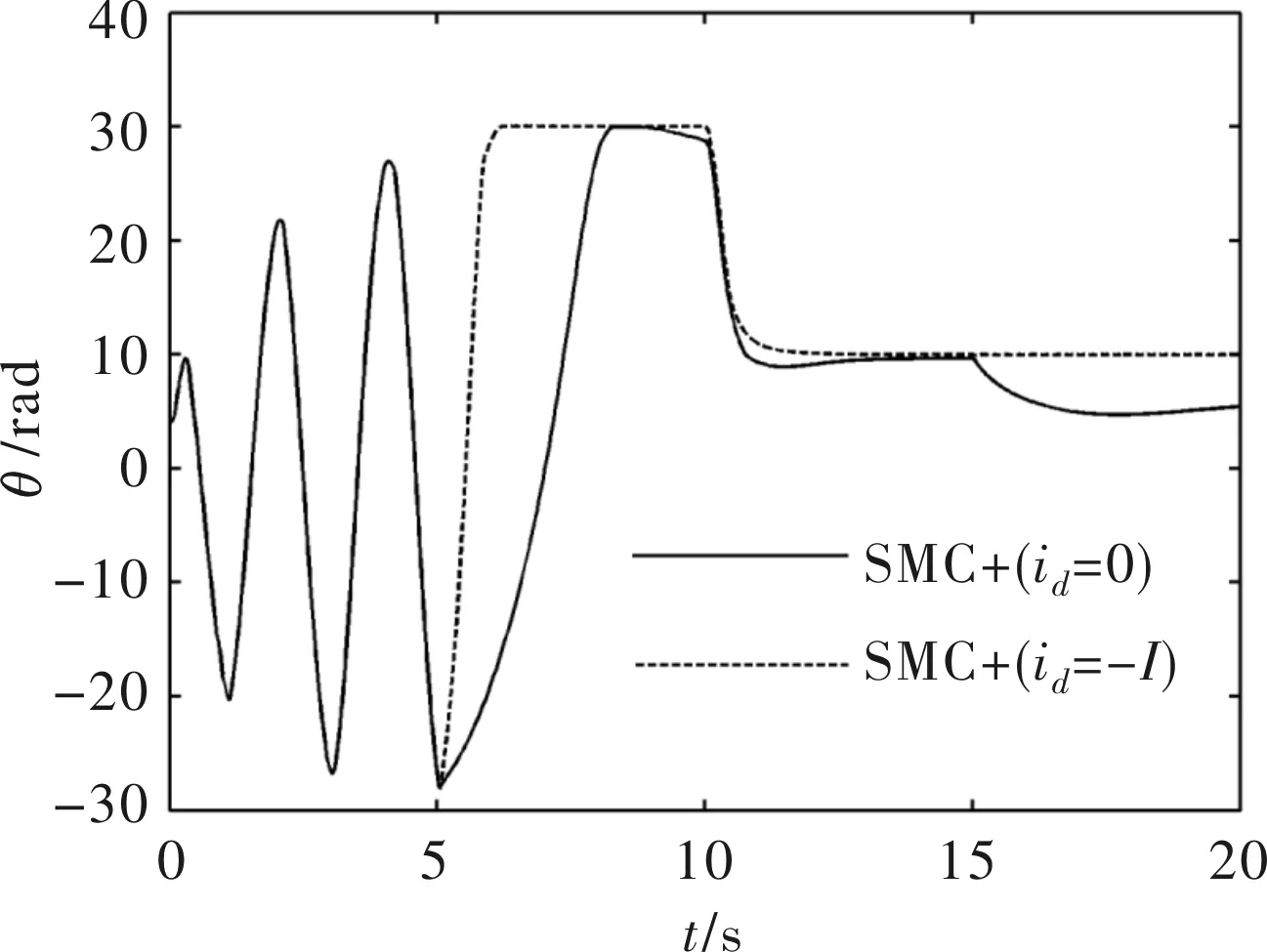
d-q坐标系下IPMSM的定子电压方程为
(1)
式中,ud、uq分别为d、q轴电压;id、iq分别为d、q轴电流;Rs为定子绕组电阻;ψd、ψq分别为d、q轴磁链;ω为转子电角速度。
d-q坐标系下IPMSM的磁链方程为
(2)
式中,Ld、Lq分别为d、q轴电感;ψaf为永磁励磁磁链。
d-q坐标系下IPMSM的电磁转矩方程为
Te=np(ψdiq-ψqid)
(3)
式中,Te为电磁转矩;np为极对数。这里考虑的是采用正交变换时的情形,如果采用的是Park变换则式(3)中会出现系数3/2。
IPMSM的运动方程为
(4)
式中,J为机械转动惯量;ωm为转子的机械角速度;θm为转子的机械转角;TL为负载转矩;D为粘滞阻尼系数;K为扭转弹性转矩系数。
本文考虑TL为位能型转矩不变型负载的情况,在这种情况下电机正向转动、反向转动以及转速为零时TL均保持不变。Kθm项表示扭转弹性转矩。考虑电机通过传动装置驱动一个和弹簧连接的位能型转矩不变型负载在一定范围内运动,并且以弹簧不发生形变时为起始位置,此时运动方程中就会出现TL项和Kθm项。Dωm项表示粘滞阻尼转矩,反映摩擦力对电机运动的影响。
ωm、θm还满足以下关系:
(5)
式中,θ为转子的电转角。
如果忽略IPMSM工作过程中Ld、Lq、ψaf的变化,则由式(1)~式(5)可得考虑扭转弹性转矩时IPMSM系统在d-q坐标系下以id、iq、ω、θ为状态变量的状态方程[13]:
(6)
将式(6)中的参数按照表1所示进行取值。
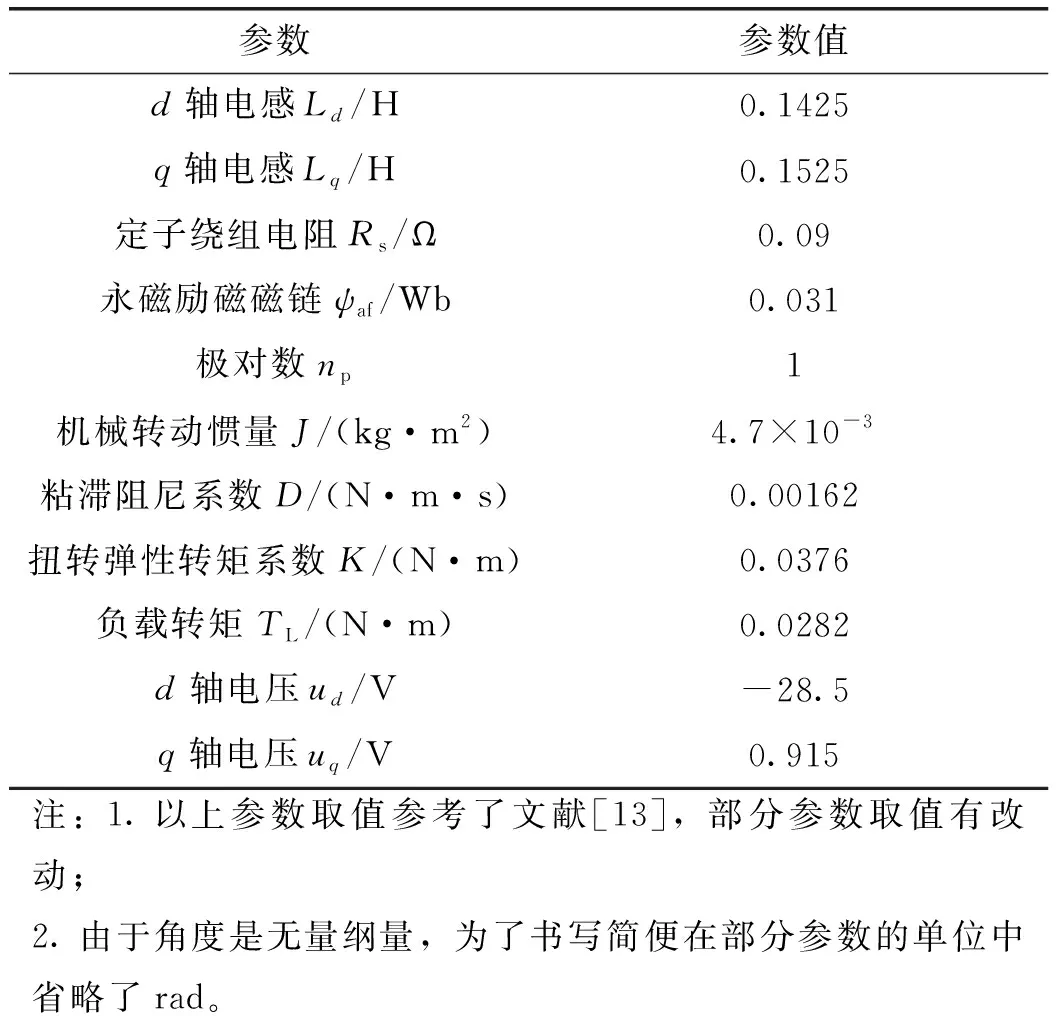
表1 IPMSM中的参数取值
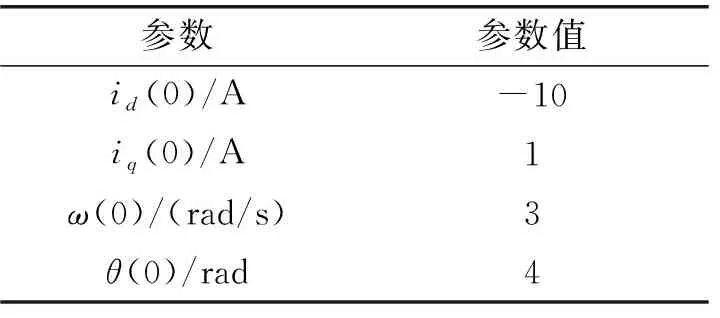
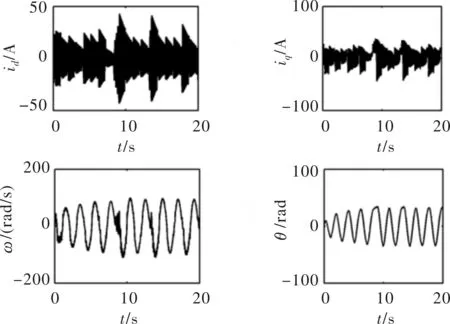
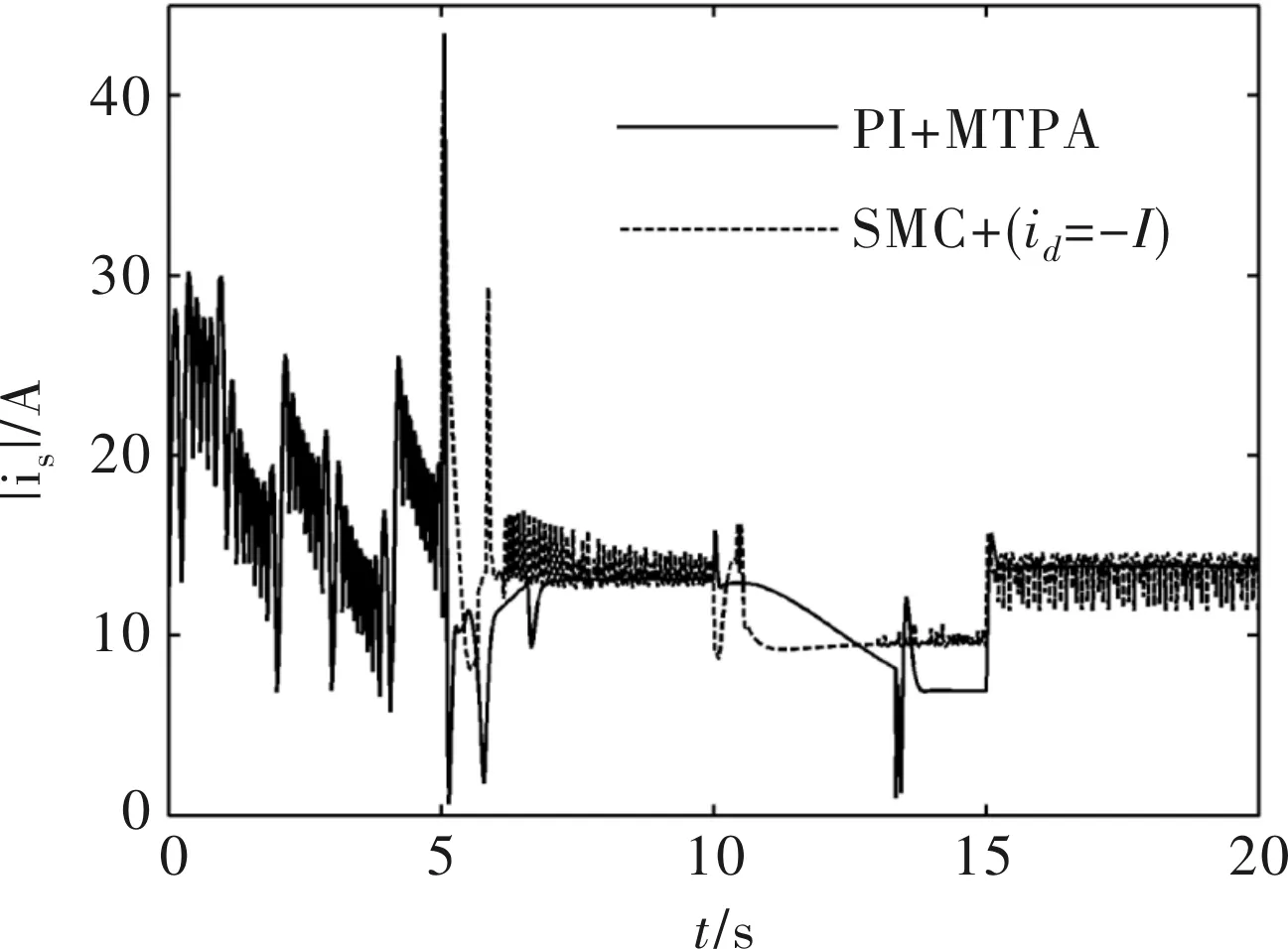
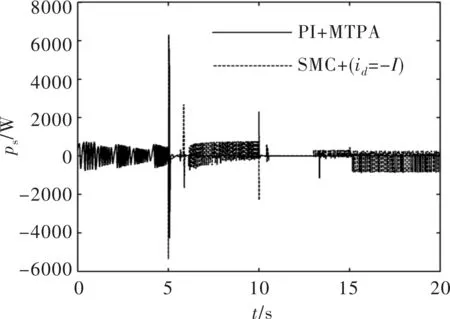
可以看到表1中Ld (7) 在表1所示取值条件下进行数值计算可以得到式(6)所示系统的Lyapunov指数(LE)如表2所示。 表2 IPMSM的Lyapunov指数(LE) 由混沌学理论可知[2,15],此时系统处于混沌状态。 选定系统初始条件如表3所示。 表3 IPMSM的初始条件 可以得到系统的状态变量时域图和状态空间相图(以id-iq-ω空间相图为例)如图1、图2所示。 图1 系统的状态变量时域图 图2 系统的id-iq- ω空间相图 图1表明系统处于不稳定状态,图2表明系统具有较为典型的混沌吸引子。图1、图2的结果可以作为表2结果的补充,进一步说明系统处于混沌状态。 对于交流电机进行位置控制最常见的控制方法是基于PI的三环矢量控制[3-4]。 位置环控制方法如下: (8) 式中,ω*、θ*分别为速度给定和位置给定,kp1、ki1分别为位置环PI控制器的比例控制系数和积分控制系数。 速度环控制方法如下: (9) 在电流环控制方面,对于SPMSM通常采用id=0控制。对于IPMSM则通常采用MTPA控制[4],该控制方法可以最大限度利用IPMSM的磁阻转矩,提高电机单位定子电流的转矩输出能力,在输出转矩一定时则可以使电机电流最小。MTPA控制的具体方法为 (10) (11) (12) (13) 式(8)~式(13)构成了一种基本的位置控制系统。因为该控制系统是基于PI控制的,并在电流环使用了MTPA控制策略,所以在本文中将其简记为PI+MTPA控制系统。 电机定子电压us的幅值|us|、定子电流is的幅值|is|和定子功率ps反映了控制系统对电源变换装置输出电压、电流和功率能力的要求。上述3个物理量的表达式如下: (14) 应该对上述3个物理量进行考察,看它们是否处在合理的范围。同时还应该考察电机的转速ω,它反映了控制系统对电源变换装置输出频率范围的要求。 在对上述PI+MTPA控制系统进行仿真调试的过程中可以发现,如果位置给定与控制系统切入时电机的实际位置差值较大,则位置环PI控制器的控制系数kp1、ki1就要取较小的值才能使控制收敛。但是较小的kp1、ki1又会导致出现较大的超调以及系统稳定后对负载变化的鲁棒性较差。为了解决这一矛盾,本文并采用了依据位置给定值与位置实际值的差值大小改变位置环PI控制器系数的策略。 位置给定值与位置实际值的差值即位置误差信号定义如下: e=θ*-θ (15) 采用滞回比较机制设置两个误差大小的阈值|e|th+、|e|th-,且|e|th+>|e|th->0,则控制系数的切换机制可以表示如下: 当|e|>|e|th+时,kp1、ki1取较小的值; 当|e|≤|e|th-时,kp1、ki1取较大的值; 当|e|th-<|e|≤|e|th+时,kp1、ki1保持原值(如果控制切入时|e|即处在此区间,则kp1、ki1取较大的值)。 由于IPMSM处于混沌状态时其动力学行为十分复杂,具有明显的非线性系统的特点,而对非线性系统使用滑模控制往往可以取得较好的控制效果,所以本节将在位置环引入一种基于趋近率的滑模鲁棒控制[5-6,14]来设计控制系统。 设计滑模函数s为 (16) 式中,c为常数,且有c>0,控制的收敛速度与c值有关。 (17) 式中,ε和k均为常数,它们与滑模函数s向s=0切换面趋近的速率有关。dc满足如下关系: (18) 式中,dU为随着负载TL的变化,TL/J可能达到的最大值,即: (19) dU的取值需要根据具体的情况来确定,足够大的dU可以保证系统对于负载TL的变化具有鲁棒性。 式(16)~式(19)即构成了位置环控制方案。 由式(9)可知,在第2节的PI+MTPA控制系统中,速度环PI控制器可以给出定子电流给定,再由式(10)~式(13)即可应用MTPA控制策略。 针对这一问题本文采用了将id的给定设置为某一适当负值I的控制策略。具体表示如下: (20) 这里的I值可以通过试凑法选取,也可以参考相同负载条件下使用PI+MTPA控制系统时的d轴电流id来确定。本文中将这种控制策略称为id=-I控制。 式(20)和式(12)、式(13)一起就形成了电流环控制方案。电流环控制方案再结合式(16)~式(19)所示的位置环控制方案就形成了第二种基本的位置控制系统。本文中将这一控制系统简记SMC+(id=-I)为控制系统。 当|e|>|e|th+时,c取较小的值; 当|e|≤|e|th-时,c取较大的值; 当|e|th-<|e|≤|e|th+时,c保持原值(如果控制切入时即处在此区间,则c取较大的值)。 在Matlab/Simulink中搭建模型对以上两种控制系统的性能进行验证。 首先让式(6)所示的IPMSM在表1所示的参数条件和表3所示的初始条件下运行。如第1节所述,此时IPMSM将处于混沌状态。在5 s时将PI+MTPA或SMC+(id=-I)控制系统切入。控制切入时电机的实际位置为θ(5 s)=-27 rad。位置给定设置为θ*=30 rad,并在10 s时阶跃变化为。在15 s时负载TL由0.0282 Nm阶跃变化为0.893 Nm。 PI+MTPA控制系统中的各个参数设置如下: SMC+(id=-I)控制系统中的各个参数设置如下: 两种控制系统作用下IPMSM的位置(转角)θ随时间的变化如图3所示。 图3所示的结果表明两种控制系统均能实现有效的控制,其中SMC+(id=-I)控制系统收敛速度更快,对位置给定的阶跃变化响应更快,对负载的阶跃变化鲁棒性更强。 图3 位置(转角)θ随时间的变化 两种控制系统作用下|us|、|is|和ps随时间的变化如图4~图6所示。 图4~图6的结果表明两种控制方案下电机的定子电压、电流和功率都处于合理范围。 图4 |us|随时间的变化 图5 |is|随时间的变化 图6 ps随时间的变化 由图5可以看出两种控制系统作用下电机平稳运行时的定子电流比较接近,这说明在SMC+(id=-I)控制系统中选择I=9 A是比较合适的。 两种控制系统作用下IPMSM的角速度ω随时间的变化如图7所示。 图7 角速度随时间的变化 由图7可知,仿真实验过程中IPMSM没有出现很高的转速,期间有些时段的转速还比较低,这意味着两种控制系统都要求电源变换装置和电机具有较好的低频特性。 如果令SMC+(id=-I)控制系统中的I=0,则该控制系统退化为SMC+(id=0)控制系统。但此时控制系统的鲁棒性会变的很差,为了改善鲁棒性要将控制系统中的k值由3.5提高到5。其他条件保持不变。 SMC+(id=0)控制系统和SMC+(id=-I)控制系统的控制效果对比如图8所示。 图8 SMC+(id=0)控制系统和SMC+(id=-I)控制系统作用下的位置变化 由图8可知SMC+(id=0)控制系统的收敛速度较慢,鲁棒性较差。 SMC+(id=0)控制系统和SMC+(id=-I)控制系统作用下电机的定子电流对比如图9所示。 图9 SMC+(id=0)控制系统和SMC+(id=-I)控制系统作用下电机的定子电流变化 由图9可知SMC+(id=0)控制系统作用下电机的定子电流更大。 本文基于d-q坐标系下考虑扭转弹性转矩时 IPMSM的系统模型对其处于混沌状态时的位置控制方法进行了研究。主要结论如下: (1)本文中设计的PI+MTPA控制系统和SMC+(id=-I)控制系统均能对考虑扭转弹性转矩时处于混沌状态的IPMSM进行有效的位置控制,其中SMC+(id=-I)控制系统收敛速度更快,对位置给定的阶跃变化响应更快,对负载的阶跃变化鲁棒性更强。 (2)两种控制系统作用下电机的定子电压、电流和功率都处于合理范围,两种控制系统都要求电源变换装置和电机具有较好的低频特性。 (3)与采用id=0控制策略相比,在SMC+(id=-I)控制系统中电流环适当采用id=-I控制策略可以提高控制性能并减小电机电流。

2 基于PI的三环矢量控制系统设计
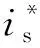
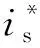
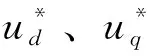
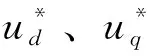
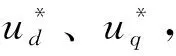
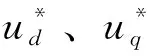
3 位置环使用滑模鲁棒控制的控制系统设计

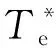
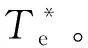
4 仿真实验
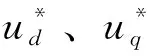
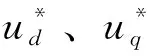




5 结 论

