巧借两点距离公式 妙解空间应用问题*
⦿江苏省苏州实验中学
钱 宁
1 线段的长度问题
线段的长度问题往往可以直接转化为空间两点间的距离问题,利用对应的距离来进一步分析与应用.
例1在空间直角坐标系中,点A(1,2,-1),点C与点A关于平面xOy对称,点B与点A关于x轴对称,则|BC|的值为( ).
分析:先根据条件中的轴对称、面对称来确定相应点的坐标,再利用空间中两点间的距离公式直接求解即可.

点评:空间中两点间的距离公式除了可直接求解对应线段的长度外,还可以间接用来确定平面几何图形的边长、形状等相关问题,此时直接利用空间两点间的距离公式转化是最基本、最有效的方法.
2 坐标的求解问题
坐标的求解问题往往直接转化为空间中两点间的距离问题,利用已知的距离通过相应的方程来求解对应的坐标.
例2在空间直角坐标系中,已知点A(4,5,6),B(-5,0,10),在z轴上有一点P,使|PA|=|PB|,则点P的坐标是______.
分析:根据条件设点P(0,0,z),由|PA|=|PB|结合空间两点间的距离公式建立关系式,通过解方程来确定参数z的值,进而确定点P的坐标.
解析:设点P(0,0,z),则由|PA|=|PB|,可得
解得z=6,即点P的坐标是(0,0,6).
故填答案:(0,0,6).
点评:在空间直角坐标系中,往往先设出相应点的坐标,再利用题设条件建立相关式子,进而确定对应的坐标.这是解决坐标的求解问题比较常见的一种思维方式.
3 参数的确定问题
利用空间两点间的距离公式可以解决对应的参数问题,涉及相应点的某个坐标参数、比值等.此类问题的求解往往结合空间两点间的距离公式确定相应的参数值.
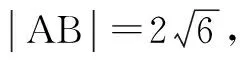
A.-3或4B.6或2C.3或-4D.6或-2
分析:根据空间两点间的距离公式建立关于x的二次方程即可确定参数x的值.
解析:根据空间两点间的距离公式,得
整理得(x-2)2=16,解得x=6或-2.
故选:D.
点评:在空间直角坐标系中,两点间的距离公式中包含七个量,即两个点的横坐标、纵坐标、竖坐标,以及对应的距离.已知其中六个量就可以求出剩下的一个量.
4 距离的最值问题
距离的最值问题往往通过空间两点间的距离公式转化为函数问题,进而利用函数的性质求解对应的距离的最值.
例4在空间直角坐标系中,试在xOy平面内的直线x+y=1上确定一点M,使它到点N(6,5,1)的距离最小,此时点M的坐标为______.
分析:根据条件设出点M的坐标,利用空间两点间的距离公式表示|MN|,通过配方法结合二次函数的图象与性质即可确定最值.
解析:由点M在直线x+y=1(xOy平面内)上,可设M(x,1-x,0),那么
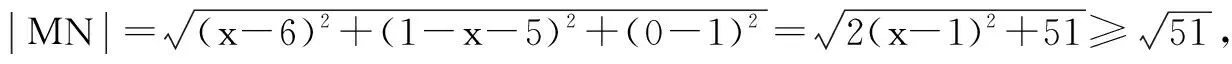

点评:由于空间两点间的距离公式中的坐标都带有平方,因此,利用距离公式求最值问题时,往往要通过转化,利用二次函数的图象与性质加以分析与求解.
5 轨迹的方程问题
轨迹的方程问题往往通过假设相应点的坐标,利用空间两点间的距离公式建立相应的关系式,进而求解相关方程.


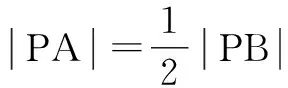
点评:此类问题建立在空间两点间的距离公式的基础上,通过公式的转化来确定相应的轨迹.平面直角坐标系下的很多方法可以推广到空间直角坐标系中,点的轨迹的求法就是一个典型的推广.
6 知识的综合问题
空间中点、线、角等相关的综合问题往往通过空间直角坐标系的建立,结合空间两点间的距离公式的应用来解决.

图1
例6如图1,在棱长为1的正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系O-xyz.
(1)若点P在线段BD1上,且满足3|BP|=|BD1|,试写出点P的坐标,并写出P关于y轴的对称点P′的坐标;
(2)在线段C1D上找一点M,使点M到点P的距离最小,求出点M的坐标.
分析:(1)根据点P在线段BD1上,且满足3|BP|=|BD1|确定点P的坐标,再结合对称性确定点P′的坐标;(2)根据空间两点间的距离公式确定|MP|的关系式,通过二次函数的配方,并结合相应的图象与性质确定最值.

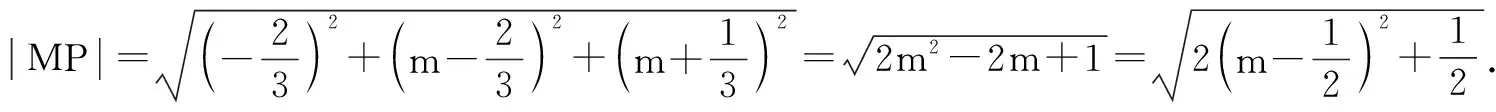
点评:解决此类空间的综合问题,首先是建立合适的空间直角坐标系并列出相应点的坐标,利用点的位置,结合中点坐标公式、距离公式,以及点的对称等性质来解决相应的综合问题.
7 结束语
空间两点间的距离公式作为一种工具,其应用非常广泛,不仅只局限于此.随着学习的深入,我们会越来越深刻地体会到,只要是空间直角坐标系中的相关问题,大都有空间两点间的距离公式的影子存在,它是解决空间直角坐标系中问题的一个有力工具.

