核心素养理念下的高中数学单元教学设计与实践
⦿山东省日照市海洋工程学校
王帅翔
1 引言
数学单元教学设计是从整体角度来进行的,并非舍弃课时教学.在教学大纲的指引下,数学教师要结合教材内容精心设计问题,把本单元内容整合为前后关联的整体,在授课中落实学科核心素养.鉴于此,本文中结合“圆锥曲线”单元内容展开教学,希望对大家有所帮助.
2 单元教学的整体设计
圆锥曲线内容包括椭圆、双曲线和抛物线,它们在多个方面存在着很大相似度,内容上有着很大的关联.一般而言,教材章节前言首先引出大单元的学习内容,然后分三部分展开,每一部分分别从标准方程、几何性质方面展开学习,再在最后阶段进行串联与总结.
数学思想是数学的灵魂,单元教学中要适时地渗透数学思想,用高观点、思想性去引领学生学习,有效促进学科素养的形成.单元教学设计中,教师不妨基于思想方法对教材内容重新整合,层层递进地进行授课活动.
椭圆:采用先分后总形式,结合原有知识再总结,以此为基础形成圆锥曲线学习和研究的大框架;
双曲线:结合椭圆的学习经验,展开对双曲线的学习,从而加深对解析法的认知;
抛物线:在已有知识的基础上,展开对抛物线的标准方程和几何性质的学习.再结合学生和课堂教学实际展开授课,从整体角度进行思考和研究.
3 单元教学模式下的教学实践
单元教学模式下,高中数学要统筹教学课时和教学目标.以“抛物线”知识为例,教师要达到以下教学目标:(1)精心设计问题情境,引导学生在问题情境中抽象得出数学模型,加深对知识的认识和了解;(2)建立直角坐标系,带领学生深度理解抛物线定义,求出标准方程,再得出几何性质;(3)在已有经验基础上,使学生在探究中理解和掌握知识中蕴含的数学思想,通过思考和训练,理解和掌握数学解题方法.
3.1 创设问题情境
数学课堂中,学生是课堂的“主人”,教师要做好陪伴和引导角色.随着年级增加,高中数学课程难度越来越大,一旦基础不牢固学习起来就会很吃力,如果无法联系以往学习内容,容易导致学习兴趣下降.教师课堂授课时,要结合学生以往学习经验和实际学情创设问题情境,引发课堂思考,让每个人都能参与到学习之中[1].
教师结合班级学生的实际学情,设计以下问题:
(1)在本单元学习中,你从椭圆中学到了哪些知识?椭圆研究过程中用到了哪些研究方法?
(2)如果你来学习抛物线,你的研究思路是什么?
设计意图:设计问题情境,引导学生回忆本单元中的椭圆部分知识的探究过程,为后续学习思路迁移做好铺垫,从而确定本节课的学习和研究思路.
3.2 引导学生活动
开启学生思维,需要教师进行有效组织和引导,促进抽象能力的形成和发展.在课堂中,教师引导学生学会类比,经过点拨形成严谨的数学语言,促进学生对知识的理解和掌握.课堂中,教师应结合教学目标与具体要求来设计内容,重视学生认知过程,以此为基础作为知识“生长点”,关注个体间差异性,提升抽象思维素养,有效提升学科综合水平.
教师引导学生尝试动手操作:
如图1所示,已知a,b,c,d,e,g,h,i,j为同一坐标系内的一组相互平行的直线,直线l垂直于此组直线,垂足分别为A,B,C,D,E,G,H,I,J,其中点F是直线e上的一个定点,且位于直线l外.(学生根据教师的要求,画出图形,进行观察.)
观察后,尝试折叠纸张,使A,B,C,D,E,G,H,I,J分别与点F重合,纸张的折痕分别与a,b,c,d,e,g,h,i,j相交于A1,B1,C1,D1,E1,G1,H1,I1,J1,然后用光滑曲线将A1,B1,C1,D1,E1,G1,H1,I1,J1点依次进行连接,观察最终得到的曲线.

图1
思考:得到的曲线具有哪些几何特征?曲线的形状是怎样的?
设计意图:在本单元初始课中,学生已经学习过其它知识点,教师结合以往学过的双球模型进行适度强化、实现知识的螺旋上升,安排实验操作深化对抛物线概念的理解,为接下来探究和掌握抛物线的标准方程做好铺垫,以便在单元框架内进行知识的整体构架,在学习目标引领下促进对教材内容的理解和掌握.
3.3 展开小组合作
数学课堂教学中,教师要加强引导学生对教材内容的学习和探究,要重视小组活动环节存在的共性问题,引导他们主动参与小组活动,关注学情适当调整教学内容,促使数学知识的发现,让他们能够循序渐进地完成学习目标,增强学习自信心.
结合上面得到的图形和以往的学习经验,学生要选择合适的坐标系,根据抛物线的定义列出等式,用坐标表示等式中的量,化简等式,最终求得抛物线的标准方程.学生先独立思考、然后与组内其他人沟通交流,得到最终的答案.小组讨论过程中,教师在教室内来回巡视,指导学困生思考和探究学习,及时发现学生存在的共性问题.经过观察和交流,班级学生在构建抛物线标准方程中,存在着以下三种方案:
(1)以l为y轴,过点F且垂直于l的直线为x轴建立直角坐标系(如图2);
(2)以过F点且垂直于l的直线为x轴,x轴与l交于点N,以线段NF的垂直平分线为y轴建立直角坐标系(如图3);
(3)以定点F为原点,过点F且垂直于l的直线为x轴建立直角坐标系(如图4).
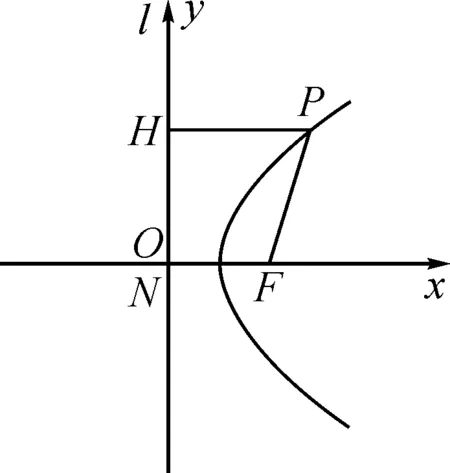
图2 方案(1)

图3 方案(2)
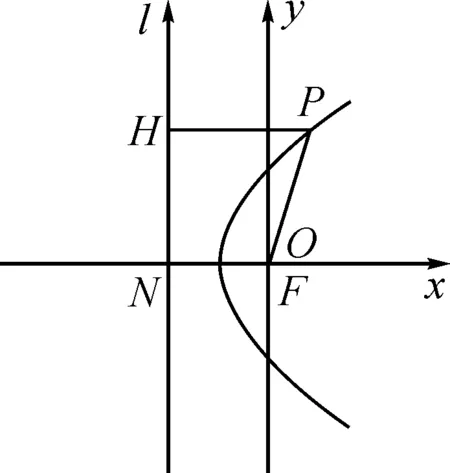
图4 方案(3)
设计意图:根据以往椭圆、双曲线的学习经验,学生在推导中尝试得到抛物线的标准方程.结合建立直角坐标系的不同思路,学生在自主探究中感受到数学的统一之美,体会到推导得出标准方程后的成就感.小组活动中,教师要引导学生进行小组合作,让每个人积极参与到讨论中,启发数学知识的发现,在思考和交流中拓展思维.
3.4 进行深度探究
在具体的教学过程中,教师要结合班级学生的实际学情和教材内容,在讲解中逐步渗透学科核心素养,通过与学生的互动交流,营造活跃的课堂氛围,在交流中培养学科核心素养.教材中有的知识点适合于课堂探究,教师要基于学生“最近发展区”理论来进行教学,引导学生在原有知识基础上进行思考和交流,激发出学生对数学学习的兴趣,将新知识内化到自身知识体系中,渗透中形成数学学科核心素养[2].
教学中,教师引导学生比较以往学过的知识:
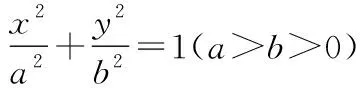
(2)根据抛物线y2=2px(p>0)的标准方程,结合以往学习经验思考抛物线应该具有怎样的几何性质?
设计意图:结合课堂中提出的问题,让学生依据图形特征加深对抛物线概念的理解,在此基础上,通过“建立坐标系—设点—列出算式—化简算式—验证证明”进行深度研究,充分理解抛物线的几何性质.在课堂教学,特别是在讨论过程中,教师要精心设计问题,适时调整教学内容,从研究抛物线入手引入本节课知识,完成对标准方程与几何性质的研究,促进学科核心素养形成.
3.5 优化课堂认知
数学教学中,教师要重视课堂小结环节,以总结方式来引导学生感受新旧知识点间的关联和区别.对于本节课来说,面对众多新内容,教师要适当引导学生对本节课学习的内容进行总结,列出表格进行区分和掌握,加强课堂小结以优化课堂认知过程.数学课堂教学中,教师要关注学生课堂学习中存在的困难,先让他们总结后再进行试题训练,让每个人在练习中有所收获,巩固课堂学习内容,加强知识的应用.
从图形、标准方程、焦点坐标、准线方程、几何性质五个方面列表,在表格中填写自己对相关内容的理解.
此外,教师还会布置一道试题强化课堂认知:已知抛物线y2=4x上的一点到焦点的距离为5,求该点的坐标.
设计意图:通过对表格内容的理论理解,在已有知识基础上适度应用新知识,考察学生对抛物线部分的理解,体现出课堂教学的整体性和关联性,让每个人在学习中发展学科素养.试题训练起到了巩固课堂新知识的效果,延续本节课内容、体现出单元教学的特点.
4 教学反思
数学教学中,教师要重视单元教学设计工作,以思想方法为引领,注重知识和学习经验的迁移,将单元设计的理念贯穿于各个小单元中,从而实现知识的螺旋上升,在授课中发展学科核心素养[3].
从单元到课时,教师从问题情境设计、引导学生活动、展开小组合作、进行深度探究和优化课堂认知方面展开教学,站在制高点审视本单元内容,从思想化、结构化视角对本单元教学内容进行整体设计,课时实施中融入数学思想.只有这样,高中数学课堂才能“既见森林又见树木”,让数学深度学习落实于课堂的每一个细节之中[4],从而带领班级学生在学习中掌握学科思想、发展思维能力,有效提升学生数学综合水平.

