例析创新试题对创新思维能力的培养*
⦿秦皇岛市第一中学
孙 丽
数学文化是从数学观念、问题、思想、方法、典故等角度,渗透到高中数学教学中,让学生深入了解数学历史,拓宽对数学的认识,从而点燃学生对数学学习的火花[1],感悟数学思想方法,激活创造潜力,提升数学核心素养.
1 新定义
新定义是创新发现新事物,揭示文化新规律,创造新的思想方法、解决新问题的思维过程.这种思维可能并不是第一次出现,但对于思维主题本身而言,这次的发现认识超越常规思维,需要同学之间相互合作、交流,突破传统,感悟新知,解决当前问题.

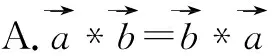



分析:该题是利用新定义逐个分析判断,属于向量数量积的定义范围.



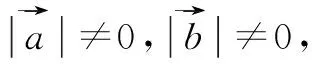

所以选:ABD.
2 数学美
数是美的元素,数学是美丽的学科,数学用它独特的美,点缀着我们的生活.数学可以继承美,也可以创造美.中国文化倡导至善至美,这与数学文化追求的数学之美相得益彰,这是数学的文化魅力.数学之美有其表现形式的美,也有内容严谨的美,有公式美、结构美、语言美、逻辑美、表达美、应用美和创造美[2].这是一种优雅的美,一种令人震撼的美.通过让学生感受数学美,追求数学美,能更好地激发学生的思维之美,创造魅力无穷的空间之美.
例22022年北京冬奥会开幕式中,当《雪花》这个节目开始后,一片巨大的“雪花”呈现在舞台中央,十分壮观.理论上,一片雪花的周长可以无限长,围成雪花的曲线称作“雪花曲线”,又称“科赫曲线”,是瑞典数学家科赫在1904年研究的一种分形曲线.如图1是“雪花曲线”的一种形成过程:从一个正三角形开始,把每条边分成三等份,然后以各边的中间一段为底边分别向外作正三角形,再去掉底边,重复进行这一过程.

图1
若第1个图中的三角形的周长为1,则第n个图形的周长为________;若第1个图中的三角形的面积为1,则第n个图形的面积为________.
分析:雪花之美与数学知识数列结合,第一空由图形之间的边长的关系,得到周长是等比数列,再按照等比数列通项公式可得解;第二空由图形之间的面积关系及累加法,结合等比数列求和可得解.
解:记第n个图形为Pn,三角形边长为an,边数为bn,周长为Ln,面积为Sn.



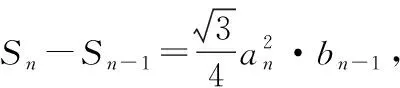
…………
利用累加法,可得
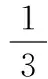
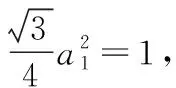
所以,
故

3 数学史
数学史是揭示数学知识的发展,展现数学思维的过程[3].通过数学史的学习,从文化角度增强学生对数学的理解与学习,激发探索数学的热情.

分析:已知含参数λ的方程f(x,λ)=0有解的问题,我们可分离出参数λ,将方程化为F(λ)=g(x),根据g(x)的值域,求出F(λ)的范围,继而求出λ的取值范围.


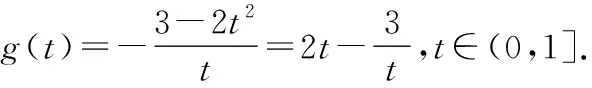

又因为g(1)=-1,t→0+时,g(t)→-∞,所以g(t)的值域为(-∞,-1].
因此λ+1∈(-∞,-1],所以实数λ的取值范围为(-∞,-2].
故填答案:(-∞,-2].
4 结语
寻找数学进步的历史轨迹,领会数学的美学价值.数学文化融入数学课堂,增强课堂生动性的同时,加强互动交流,促使学生挖掘蕴涵在数学课堂中的思想方法,提升学生自身的文化价值和创新意识,形成和谐全面发展、终身学习的新时代青年.

