基于迭代缩减窗口自助软收缩算法的近红外光谱变量选择方法研究

徐啟蕾，郭鲁钰，杜 康，单宝明，张方坤

（青岛科技大学 自动化与电子工程学院，山东 青岛 266061）

在近红外光谱和高光谱成像中，许多变量冗余或存在噪声干扰；此外，高维数据存在“维数灾难”，即当建模所涉及的变量数量远超过样本数量时，回归模型的准确性会随着变量的增加迅速下降。因此需要使用变量选择技术来提取重要变量，提高模型的预测能力和运算速度，增强其鲁棒性和可解释性［1］。根据选择的数据特征，变量选择技术可分为单变量选择和区间变量选择［2］两种。单变量选择方法将每个变量视为一个单位，区间变量选择将多个连续变量视为一个单位。大量单变量选择方法已经被提出，例如：连续投影算法［3］、遗传算法［4］，以及许多基于模型种群分析策略（MPA）的变量选择方法，包括竞争自适应重加权采样（CARS）［5］、迭代保留信息变量（IRIV）［6］、变量组合种群分析（VCPA）［7］、变量迭代空间收缩法（VISSA）［8］、自助软收缩（BOSS）［9］等。但单波长选择方法存在稳定性较差，易受噪声影响等问题，使其所选变量与化学性质之间的关系无法被有效解释，通过引入区间进行变量选择能较好地解决这些问题。近几十年发展了众多区间变量选择方法，如：区间偏最小二乘（IPLS）法［10］、移动窗口法（MW）［11］、区间VISSA法［12］、Fisher最优子空间缩减（FOSS）法［13］等。但区间选择算法十分依赖于区间的划分，若划分过于简单或固定，则难以找到最优模型；而过于强调最优区间，则会使得算法变得复杂且运行缓慢。

针对上述问题，本文提出了一种更为简便灵活的迭代缩减窗口策略（ISW），该策略在迭代选择的过程中加入一个逐步缩减的窗口，通过窗口采样增加所选变量的连续性和算法的稳定性，并通过迭代缩减策略确保选择的准确性和算法的灵活性，该方法可以集成在许多基于MPA 策略的变量选择算法过程中。在此基础上，本文通过改进BOSS算法，形成了一种新的变量选择算法——迭代缩减窗口自助软收缩（ISWBOSS）算法。该算法对窗口进行加权采样，利用子模型竞争筛选出最优的建模变量。通过在公开的玉米近红外光谱数据集上进行测试，证明了方法的有效性。

1 算法原理

1.1 模型种群分析和迭代缩减窗口

1.1.1 模型种群分析模型种群分析策略，最早由Li 等［14］引入到光谱变量选择中，其核心思想是对随机生成的大量子模型的输出进行统计分析，从数据中提取感兴趣的信息［15］。在基于MPA 策略开发的算法中，BOSS算法是较为优秀的代表，其具体原理可以从文献［9］中得到。

BOSS 算法利用优秀偏最小二乘（PLS）子模型的回归系数对变量进行加权抽样来实现软收缩，使用后文提到的玉米光谱数据模拟其迭代过程，如图1A所示。可以看出，在迭代初期变量的选择频率呈现局部块状。这是由于连续光谱变量之间存在很强的共线性，大量抽样后这些共线性变量的回归系数趋于均值，使得局部被选频率也大致相同。但抽样次数过多会导致算法运算效率下降，而减少抽样次数将使这些共线性变量的回归系数变得不稳定，导致变量的重要性无法被准确地评估。另外随着迭代的进行，变量空间非均匀收缩，打破了这种局部连续共线性，使得BOSS算法选择的区域逐渐变为单一变量。一些宽度较窄的特征峰，还可能会因其他特征峰变量抢占剩余变量空间而被过早滤除。

1.1.2 迭代缩减窗口采样基于上述分析，为了更好地利用近红外光谱数据的特点，本文提出了一种迭代缩减窗口的加权采样策略，其具体过程如图1B所示。首先将数据中所有变量的权重初始化为相同的值w0，权重和为1。设定一个初始的窗口大小，并将变量按顺序划分为一定数量的窗口，窗口内变量的权重累加得到窗口的权重。对窗口进行N次加权抽样，每次被抽到的窗口内的变量全部参与子模型建模。根据MPA 策略，设定合适的评价指标对子模型进行统计比较，并更新每个波长变量的权值。随后按预设缩减方式迭代缩减采样窗口的大小，预设缩减方式有每次迭代窗口大小减一或直接除二，也可以根据数据的特性自定义合适的缩减方式。按缩减后的窗口大小重新划分窗口，并计算新窗口的权值。继续对窗口进行加权采样，直到剩余被选变量数均值小于2。

图1 BOSS算法在迭代过程中变量选择频率图（A）及迭代缩减窗口的示意图（减一方式）（B）Fig.1 Frequency of variable selection during iteration for the BOSS algorithm（A）and schematic diagram of the iterative shrinkage window（minus one approach）（B）

分析上述过程可以得出，通过对窗口进行抽样，变量的局部被选频率呈现出更加稳定的块状，避免了单变量采样过程中因随机性导致的部分特征的遗失。另外由于光谱数据的有效信息是连续存在的，相比单变量抽样，有效窗口与无效窗口在一次抽样中的差异会更加明显，筛选的效率也更高。随着迭代的进行，窗口大小逐步缩减，使得算法可以在共线性变量间进行精细筛选，其中采用减一缩减方式的窗口类似于后向选择方式，而除二方式更类似于二分位查找的方式。相比单纯依赖权重的随机抽样，这两种方式能更好地利用每次缩减前后的信息变化。

1.2 ISWBOSS算法的实现步骤

通过将迭代缩减窗口采样策略与BOSS算法结合，得到ISWBOSS算法，具体步骤如下：

Step 0：设置初始窗口大小，赋予校正集变量相同的初始采样权值；

Step 1：将校正集样本的变量空间按窗口大小均分为相应的窗口；

Step 2：将每个窗口内变量的权值相加得到窗口的采样权值；

Step 3：运用加权自助采样对窗口空间进行N次采样，统计被选窗口内剩余变量的均值，并计算基于每次采样被选窗口内变量建立的PLS模型的交叉验证建模均方根误差（RMSECV）；

Step 4：保留RMSECV最小的前10%模型的建模变量为优秀变量子集，统计其回归系数，进行归一化处理，得到每个变量的新权重；

Step 5：按缩减策略缩减窗口大小；

Step 6：判断剩余变量的均值是否小于2，如果否，返回Step1；

Step 7：选择迭代过程中RMSECV 最小的模型，其建模变量即是最终选择的变量。

2 实验部分

2.1 玉米数据集

使用最常用的玉米近红外公开数据集（从网站http：//www. eigenvector. com/data/Corn/index. html获取）进行测试。近红外光谱数据如图2所示。数据由m5光谱仪测量的80个玉米样品组成，并包含每个玉米样本的水分、油脂、蛋白质和淀粉含量。光谱范围为1100 ～2498 nm，间隔为2 nm，共包含700个波长点。将数据集随机划分为包含60个样本的训练集和20个样本的测试集。

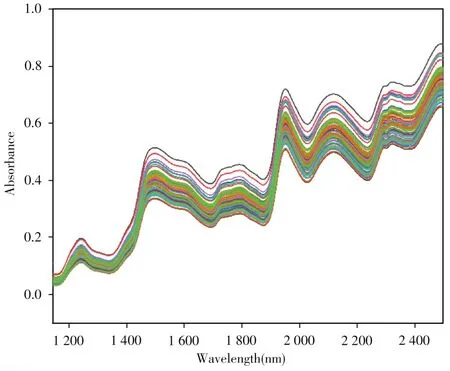
图2 玉米数据的近红外光谱Fig.2 Near-infrared spectra of corn data

2.2 软 件

本文在一台安装有Matlab R2020a 的个人计算机上进行测试。该计算机装配的CPU 型号为英特尔i7-10875H，运行内存大小为16 G，操作系统为Windows 10。

3 结果与讨论

3.1 窗口大小与缩减方式的影响

影响ISWBOSS算法性能的主要参数是初始窗口大小和每次迭代窗口的缩减方式。为了验证其对性能的影响，令初始窗口大小从10 ～100 变化，间隔为10，每次迭代窗口以除二和减一方式缩减。以玉米蛋白质数据为例，重复运行20次，并记录每轮迭代和每次运行的RMSECV 值，得到如图3所示的曲线图。

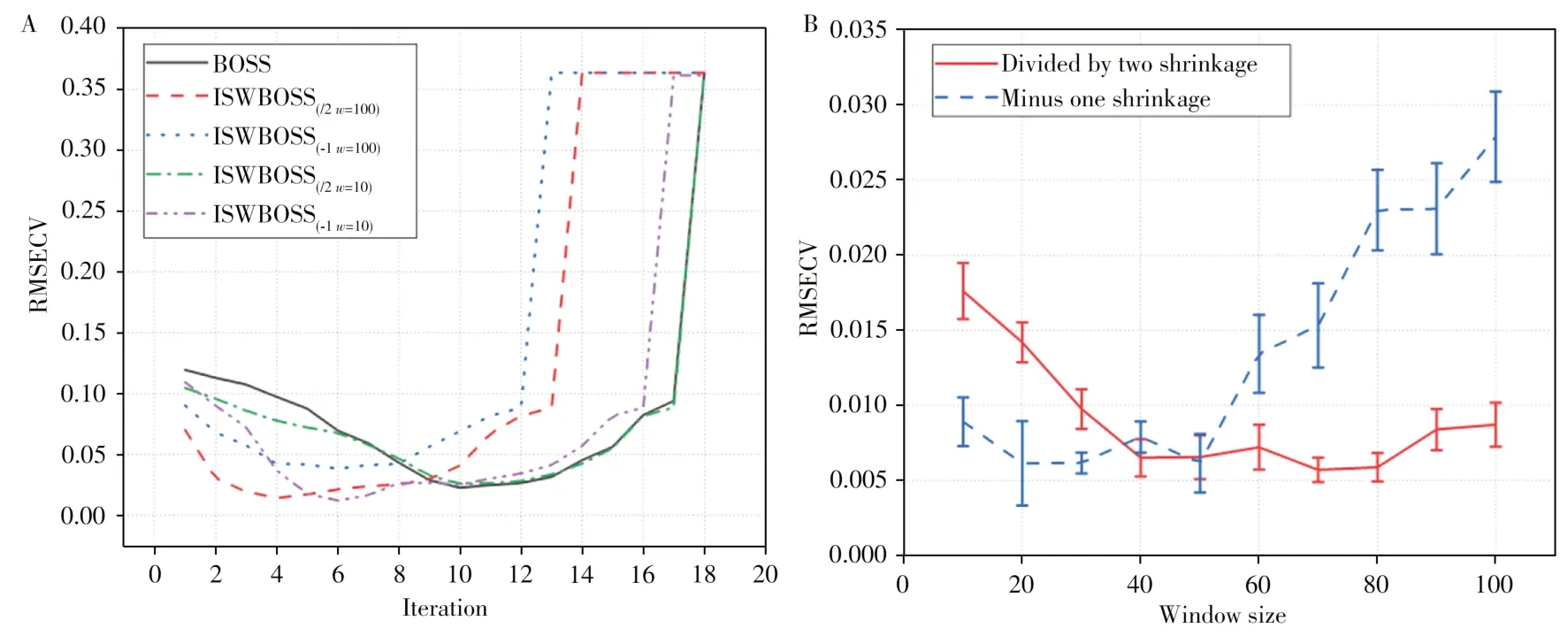
图3 以玉米蛋白质数据为例，不同缩减方式的ISWBOSS与BOSS每次迭代的最优RMSECV（A）及ISWBOSS的缩减方式与窗口大小对模型RMSECV的影响（B）Fig.3 Take corn protein dataset as an example，optimal RMSECV for each iteration of ISWBOSS and BOSS with different shrinkage methods（A）and effect of shrinkage method and window size of ISWBOSS on model RMSECV（B）

由图3A可以看出，与BOSS算法相比，使用迭代收缩窗口改进的BOSS算法只需更少的迭代次数即可达到RMSECV的最小值，且模型的建模效果更好。其中，当初始窗口大小设定为10并使用除二方式缩减时，其性能与原始BOSS 几乎相同。由图可以看出，从第6 次迭代开始，窗口已经缩减到最小值1，ISWBOSS变为原始BOSS算法。当迭代5次窗口未缩减为1时，ISWBOSS建立的模型明显优于BOSS，因此可以证明使用窗口采样有助于算法性能的提升。另外可以看出，初始窗口为10且使用减一缩减方式改进的算法的RMSECV在4种算法中最优。而初始窗口为100时，使用除二方式缩减的建模效果与其十分接近，且达到最优所需的迭代次数更少。

两种缩减方式与初始窗口大小对模型RMSECV的影响如图3B所示，可以看出，减一缩减方式在初始窗口较小时效果更好，而除二缩减方式的性能随着初始窗口的增大逐渐提高并趋于稳定。两种方式在初始窗口大小为50时效果基本相同，均达到最优的建模效果。因此可以得出，不论使用哪种缩减方式，初始窗口的大小都是影响算法性能的关键参数，只需使用简单的一维搜索算法即能确定其取值。ISWBOSS 通过增加一个易于确定的参数即可使BOSS 算法的性能获得大幅提升，更加简洁有效。另外从图中可以看出，相比减一缩减方式，使用除二缩减方式能更好地克服变量间的相关性，优化速度更快，模型的稳定性更好，因此首选除二缩减方式。

3.2 与其他变量选择算法的对比

为了评价ISWBOSS 的性能，本研究采用3 种普遍使用的变量选择方法，即遗传-偏最小二乘法（GA-PLS）、CARS 和BOSS 进行比较。建模之前，将所有数据进行标准化预处理。为预测玉米数据集中4 种成分含量，几种算法所选变量如图4 所示。以玉米淀粉为例，可以看出GA-PLS 选择的变量数量较多且过于分散，可能陷入了局部极小值未能继续滤除冗余变量。CARS 进一步减少了所选变量数，但仍存在许多无关变量，且一些较弱特征变量因硬收缩策略而被过早的强制去除。BOSS 算法和ISWBOSS 的选择较为类似，多集中在1700 ～1800 nm 范围区域。但ISWBOSS 在1748 ～1766 nm 内C—H 键特征波长处的选择更加稳定与集中。另外，ISWBOSS 还选择了1202 nm 区域的波长，这部分并没有被BOSS和CARS算法选择。一些研究［16］认为这个区域的光谱与玉米淀粉含量无关，但本文发现手动删除该区域的波长后，模型预测效果变差，其RMSECV 从0.0536 上升至0.0656，预测均方根误差（RMSEP）从0.0782 上升至0.0828。因此可认为这部分光谱对提高模型的预测效果有益，另外最新文献［17］也证明了这点，确认该处波长为淀粉带。虽然几种变量选择算法均依据模型的回归系数或建模均方根误差来驱动，是完全基于数据的方法，但相较其他算法，ISWBOSS 选择的更多是位于特征峰上的变量，且窗口的引入使得其在特征峰较宽的区域选择的变量更为连续，而在一些短峰上由于迭代缩减策略又使得其可以只选择最重要的波长。以上ISWBOSS算法具有很高的灵活性，选择的变量更加符合光谱的测量机理，得到的模型预测结果更加准确稳定，且更易于解释。

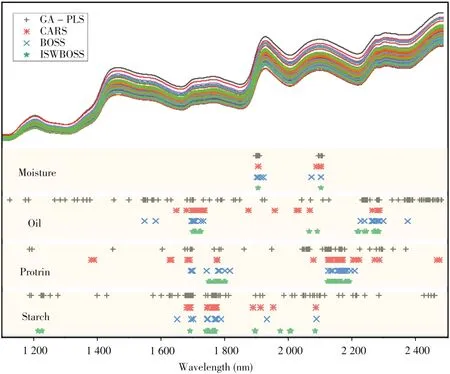
图4 不同算法对玉米淀粉数据选择的变量Fig.4 Variables selected in corn starch data by different algorithms

通过将几种算法运行50次，采用5折交叉验证，以最大潜变量数为10建立PLS 模型。使用交叉验证的RMSECV、建模决定系数（Q2

CV）、RMSEP和预测决定系数（Q2test）对模型性能进行评价，均方根误差越小，决定系数越接近1，模型性能越好。分别测试几种算法对玉米水分、油脂、蛋白质和淀粉特征选择后建立的标定模型效果，结果对比如表1所示，其中nVAR 为用于建模的变量数，nLV 为PLS模型的潜变量数。

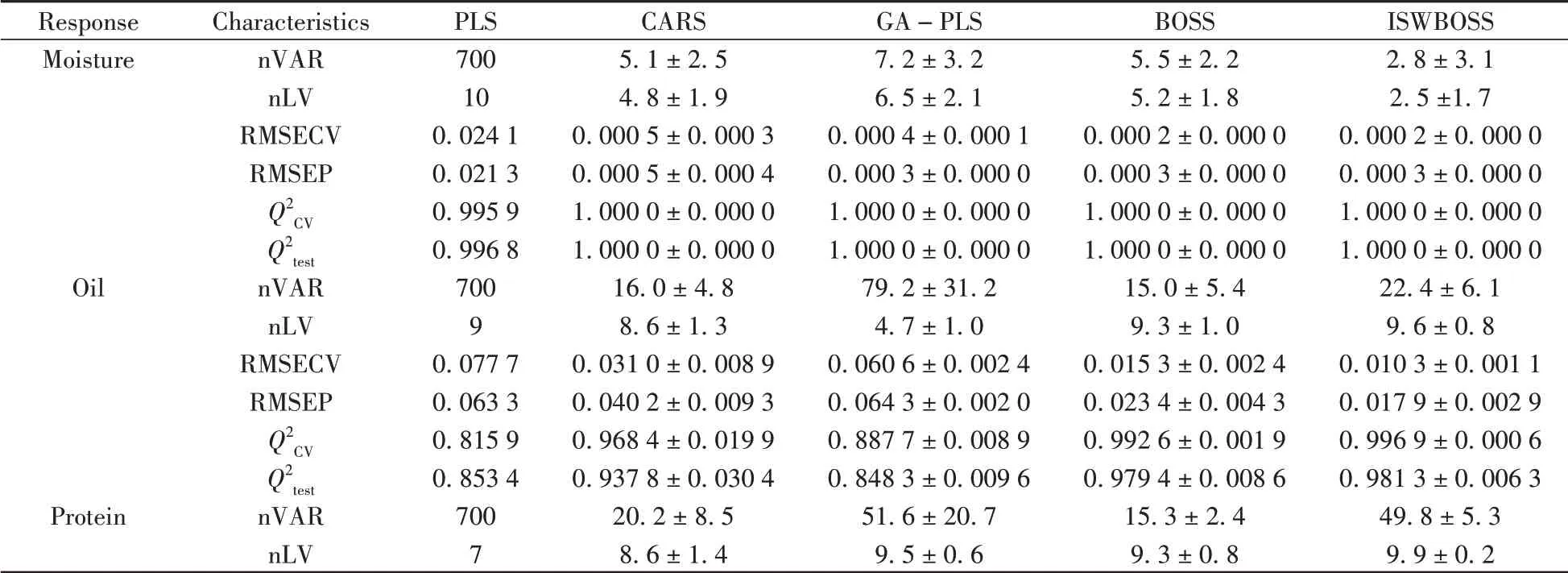
表1 不同方法结果对比表Table 1 Comparison table of the results of different methods

（续表1）

可以看出，几种算法在预测不同成分时保持了较好的性能一致性，按4 种成分Q2的平均值计算得到的性能排序为ISWBOSS ＞BOSS ＞CARS ＞GA-PLS ＞PLS，不同组分间的算法性能基本与该排序相同。相较全谱PLS 模型，所有经过变量选择建立的模型的预测性能均得以提高，说明了对近红外光谱进行变量筛选的必要性。基于几种变量选择算法建立的模型在水分预测时的性能大致相同，ISWBOSS使用了更少的变量；而对于油脂和蛋白质，ISWBOSS使用了比CARS和BOSS更多的变量，但获得了更好的预测性能。因此变量数的多少与模型的预测效果没有直接的关系，而更多的受待测属性性质和所选波数的影响。从整体效果来看，CARS和GA-PLS的预测效果大致相同，但在油脂和淀粉数据集上，CARS 的准确性和稳定性更好。原因可能是油脂和淀粉的特征波数更多［17］，优化模型变得复杂，使启发式算法更容易过拟合。与硬收缩策略的CARS相比，基于软收缩的BOSS算法和ISWBOSS算法建立的模型性能更好。由于采用RMSECV 较优模型的回归系数加权抽样，导致基于软收缩策略选择变量建立的模型RMSECV 很小，RMSEP相对较大；但其预测性能依旧优于其他对比算法，且稳定性更好，因此不能认为模型陷入了过拟合，其结果仍是可信的。与BOSS算法相比，ISWBOSS在4个数据集上均优于其他算法，证明了算法的普适性。说明窗口的引入不仅利用了连续变量的共线性，使得可以更快速稳定地区分有用和无用的变量，还可以通过不断迭代缩减的窗口进一步精细筛选其中最相关的特征，大幅提高模型的预测精度，增强模型稳定性。

4 结论

为了提高化学计量学中使用光谱建立的标定模型的性能，本文提出了一种新的ISWBOSS算法。该算法使用窗口代替对波长变量的逐个选择，更加符合近红外光谱数据的特性，避免了单波长抽样时随机性对模型的影响。在玉米公开数据集上的测试结果表明，与其他变量选择算法相比，使用ISWBOSS算法选择波长建立的模型的预测准确性和稳定性都得到了大幅提高；且与原始BOSS 算法相比，ISWBOSS 算法达到最优模型所需的迭代次数和采样次数都更少。另外迭代缩减窗口作为一种通用的改进方法，可以继续推广到其他基于MPA策略的变量选择算法中，具有一定的应用价值。