结合纹理复杂度与BEMD的灰度水印图像算法

赵慧超，胡 坤，王小超

结合纹理复杂度与BEMD的灰度水印图像算法

赵慧超1，胡 坤2，王小超1

(1. 天津工业大学数学科学学院，天津 300387；2. 中国科学院空间应用工程与技术中心，北京 100049)

本文提出并实现了一种结合纹理复杂度和二维经验模态分解(BEMD)的灰度水印图像算法。该算法首先对Arnold变换的水印图像进行BEMD分解，得到不同尺度的内蕴模态函数及余量信息。其次，对宿主图像分块进行纹理复杂度的计算，选择纹理复杂度高的区域作为嵌入位置；为了使水印图像的内蕴模态函数能与宿主图像更好地融合，对宿主图像进行了与水印图像相同筛分条件的BEMD分解。最后，将水印信息重复地嵌入到宿主图像预先选好的位置中，再对嵌入水印信息后的内蕴模态函数及余量重建得到嵌入水印后的图像。水印提取则为水印嵌入的逆过程。通过对不同纹理程度的宿主图像进行实验，得到嵌入水印后图像的峰值信噪比均在40 dB以上，面对8种常见攻击时提取水印的NC值均在0.95以上。与现有算法进行对比，该算法在大比例剪切、噪声攻击、图像滤波和JPEG压缩攻击上表现出色，且结果整体优于对比算法。

二维经验模态分解；灰度水印图像；纹理复杂度；版权保护；Arnold变换

信息媒体时代的到来丰富了人们的网络生活，数字图像、视频等多媒体信息的传输也因此变得更加便捷。在带来方便的同时，很多问题也显露出来。由于人们网络版权意识的淡薄，过于便捷地传输导致很多文本被非授权复制、修改，极大地影响了数字网络信息的发展。为保护多媒体信息的版权，数字图像水印技术得到了广泛地研究[1-4]。

数字图像水印算法依据嵌入方式分为空域水印算法和变换域水印算法。空域水印算法通过修改宿主图像中像素点的某些信息来实现水印嵌入，常见的算法有最低信息位(least significant bits，LSB)算法[5]、Patchwork算法[6]等。该类算法计算简单但鲁棒性较差。变换域水印算法通过将宿主图像从空间域转换到频域进行水印嵌入。常见的算法有基于离散余弦变换(discrete cosine transform，DCT)算法[7]、基于离散小波变换(discrete wavelet transform，DWT)算法[8]、基于离散傅里叶变换(discrete Fourier transform，DFT)算法[9]等。变换域水印算法首先对宿主图像进行某种特殊的二维变换，然后选取适合的区域将水印嵌入，最后通过逆变换将嵌入水印的宿主图像复原。在变换域上嵌入的水印信息能广泛地分布在整个宿主图像中，因此面对攻击时鲁棒性很好。依据嵌入水印图像的类型分成二值水印和灰度水印。二值水印的像素数值由0和1两种数值组成，而灰度水印的像素数值位于0～255之间，因此后者能够更详细地表达图像的信息。近年来，灰度水印凭借着储存信息量大的优点成为了数字水印的研究热点。但复杂的像素灰度值对水印的不可见性和鲁棒性也产生了一定的影响，因此灰度水印具有更加长远地研究前景。

文献[10]提出了一种结合纹理复杂度将水印嵌入到宿主图像的DWT子带中的算法，该方法极大地提高水印的不可见性。文献[11]提出一种关于DCT与DWT相结合的混合水印算法。该算法将Arnold变换后的灰度水印图像先进行DCT变换分成等大的分块，然后分别嵌入到宿主图像先进行DCT变换再进行DWT变换得到的子带上。但该算法在旋转攻击下效果较差且峰值信噪比(peak signal to noise ratio，PSNR)值较低。文献[12]利用了主成分分析(principal component analysis，PCA)与离散切比雪夫变换(discrete Tchebichef transform，DTT)相结合的算法。该算法先利用PCA将宿主图像分解成稀疏分量，再利用DTT将实质分量再次分解，最后将2D-DHCES置乱后的水印嵌入到变换后的宿主图像中，但该算法的PSNR数值明显低于其他算法。文献[13]提出了SVD-DCT-DWT相结合的水印算法。该算法使用奇异值分解(singular value decomposition，SVD)将置乱后水印的奇异特征值嵌入到宿主图像DCT变换后三级DWT变换的低频区域和高频区域。但面对椒盐、高斯等噪声时的效果较差。文献[14]提出了快速傅里叶变换(fast Fourier transform，FFT)与熵阈值匹配(entropy threshold match，ETM)相结合的算法，该算法对水印的不可加性有了一定地提高，且具有较好地嵌入容量。

自文献[15]提出二维经验模态分解(bi-dimensional empirical mode decomposition，BEMD)算法后，该算法在数字图像水印中得到广泛地应用。文献[16]利用BEMD对宿主图像进行分解选取最后一个内蕴模态函数，然后通过DCT变换将水印嵌入到中频系数中，但面对几何攻击时提取水印效果不理想。文献[17]对水印图像置乱后BEMD分解，然后对宿主图像先进行分块再进行BEMD分解，最后用水印图像分解后的3个内蕴模态函数及余量替换掉BEMD分解后宿主图像的4个分块中最后一个内蕴模态函数。分块处理虽加速了BEMD分解速度但也导致嵌入水印后的宿主图像出现了分块效应，算法不可见性明显降低。

针对上述图像水印算法存在大比例裁剪、旋转等几何攻击和噪声攻击时鲁棒性差等问题，本文结合纹理复杂度和BEMD提出了一种灰度水印图像算法。该算法首先对置乱后的水印信息进行BEMD分解，然后对宿主图像一方面进行分块计算纹理复杂度并排序选择嵌入位置，另一方面进行BEMD分解。最后在宿主图像的内蕴模态函数及余量预选择的嵌入位置上，将水印信息分别重复地嵌入到宿主图像中，重建得到嵌入水印后的图像。大量实验表明，该算法面对大比例裁剪、旋转等几何攻击及噪声攻击时鲁棒性良好。

1 经验模态分解

HUANG等[18]提出的经验模态分解(empirical mode decomposition，EMD)是一种适用于任何信号的新型频域处理方法，不需要预先设定任何的基函数，而是根据自身尺度特征分解成不同尺度的内蕴模态函数(intrinsic modal function，IMF)。文献[15]将其推广到二维图像中，并在图像融合[19]、环境预测[20]和三维数字几何处理[21]等多个领域有着广泛地应用。BEMD算法步骤如下：

步骤1.任选大小为×的图像(,)检测局部极值点，包括局部极大值和极小值。

步骤2.对检测出的局部极大值点进行曲面拟合，插值计算得到上包络，再对检测出的局部极小值点进行曲面拟合，插值计算得到下包络。

步骤3. 利用上、下包络求取平均值得到平均包络=(+)/2。

步骤4. 原始图像与平均包络面相减得到筛分的结果图像ʹ=-。

步骤5. 计算筛分终止条件，即

其中，ʹ-1(,)与ʹ(,)分别为相邻两次筛分得到的图像。

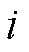
2 本文算法

2.1 Arnold变换

Arnold变换[22]是一种常用于图像加密的置乱方法。该变换具有良好的周期性，经过特定次数变换后图像像素可以回到原来的位置，因此可以对加密后的图像进行复原。对于×像素的图像，变换式为

其中，(x,y)为原始图像的像素点坐标；(x+1,y+1)为变换后图像的像素点坐标；为变换次数。置乱次数和周期可用于水印的提取，通过-次变换实现图像复原。Arnold变换的周期与图像大小有关，图像越大周期越长。对于任意>2，Arnold变换的周期≤2/2[22]。

2.2 纹理复杂度

图1 纹理复杂度计算((a)原始图像；(b)标准差图S；(c) S的二值化图；(d)纹理复杂度数值图)

(1) 计算图像的标准差图，用表示。以(,)为中心计算3×3分块的标准差为

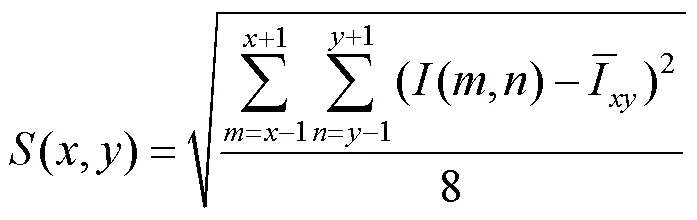
(3) 计算每一个分块的纹理复杂度，即

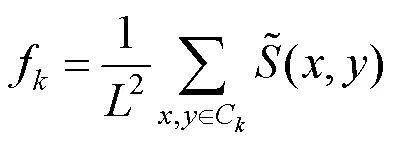
其中，C为每个分块对应的空间坐标的集合；为分块的长度；的取值在0～1之间，数值越大表示复杂度越高。图1(d)为图像Barbara的纹理复杂度数值图。由图可以看出，左侧桌布区域和右上角位置纹理复杂度数值较高，该结果与肉眼观察结果一致。

2.3 本文算法

本文提出了以BEMD为理论基础，结合纹理复杂度的鲁棒灰度水印图像算法。图2展示了算法的嵌入和提取过程。其中宿主图像Barbara大小为512×512，水印图像小熊大小为64×64。

2.3.1 水印嵌入算法

水印嵌入过程中需用到宿主图像以及灰度水印图像。

步骤1.读入水印图像，对其进行Arnold置乱，得到图像ʹ。

步骤2. 对置乱后的图像ʹ进行BEMD分解得到多尺度的1i，=1,···,和余量1。

步骤3.读取宿主图像，并对其进行与水印图像相同筛分条件的BEMD分解，得到多尺度的2i，=1,···,和余量2。

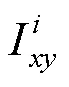
步骤5.利用式(7)将水印嵌入到选好的位置

其中，为嵌入系数；1i为水印的BEMD分解后的第层1。

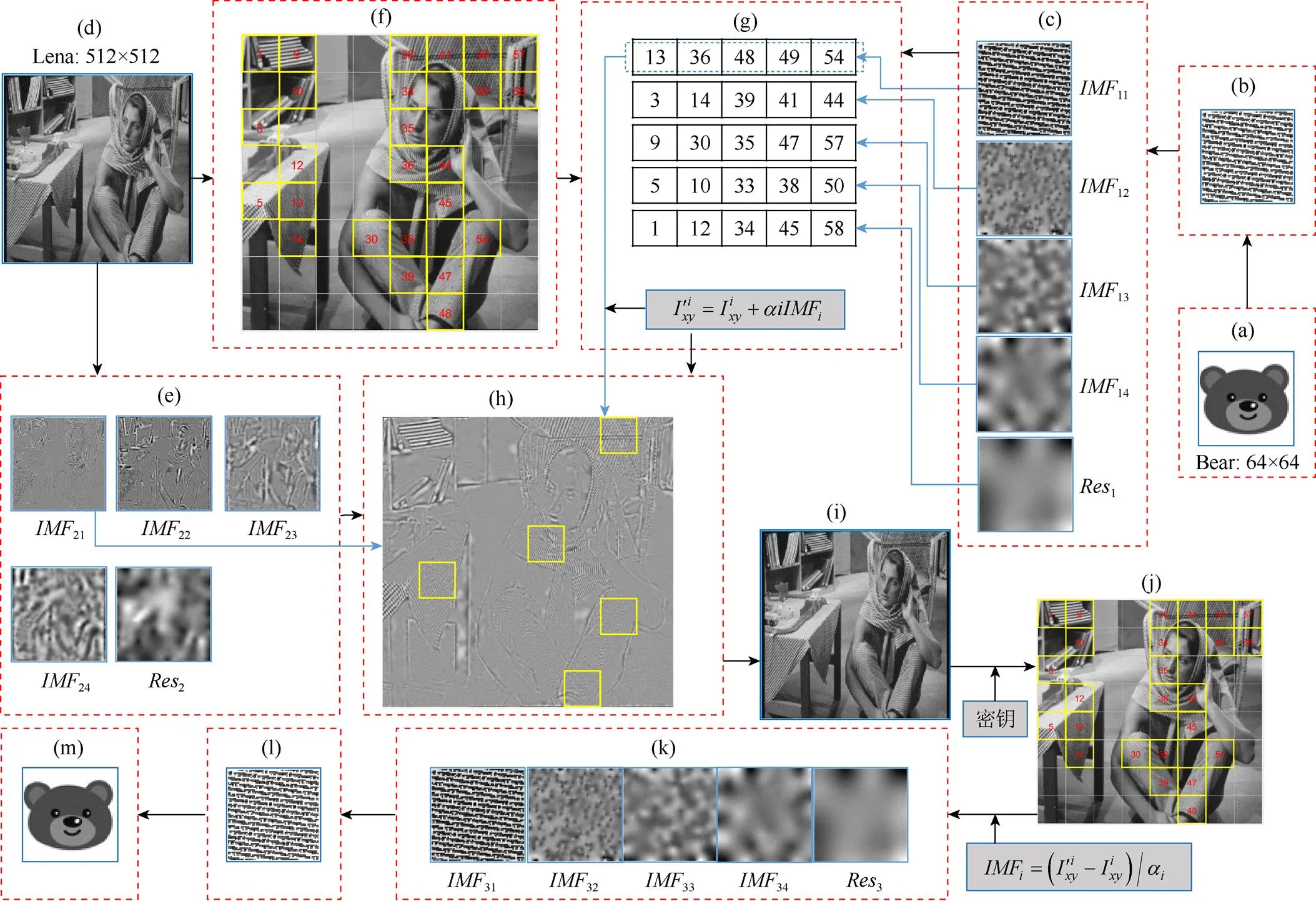
图2 算法嵌入流程图((a)水印图像；(b) Arnold；(c) BEMD；(d)宿主图像；(e) BEMD；(f)纹理检测；(g)随机分组；(h)水印嵌入；(i)嵌入水印后的图像；(j)提取水印；(k)筛选投票；(l)反Arnold：(m)水印图像)

2.3.2 水印提取算法

水印提取过程中需要的密钥包括水印嵌入系数、分块位置和Arnold置乱次数。

步骤1. 读取嵌入水印信息后的图像ʹ。

步骤2.根据嵌入位置提取水印信息，即

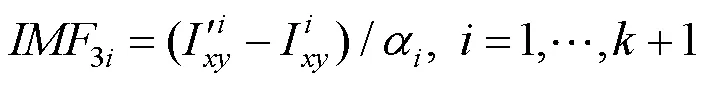
由于水印图像的1i及余量1在嵌入过程中在多个位置进行嵌入，因此在步骤3中得到的水印信息图像ʹ含有多个水印1i和余量1。为增强水印的鲁棒性，通常对水印图像像素点进行投票选出出现次数最多的点组成最终的水印图像。如果图像受几何攻击后，会有部分水印残缺，则需要在未受到攻击的地方整合出一个完整的水印图像。该处理方式减小了大比例裁剪、旋转等几何攻击和噪声攻击对提取水印的影响。

3 实验结果分析

3.1 评价指标

由于嵌入水印后的图像与原图像的质量会有一定的差异。通常采用PSNR来评价处理后图像的质量，即

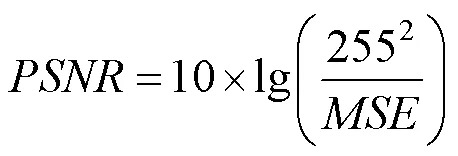
其中，为宿主图像与添加水印信息后图像的均方误差；在鲁棒水印算法中，为添加水印信息后宿主图像的不可见性。数值越大代表嵌入的水印图像越不易被察觉。

为评价提取水印与嵌入水印的相似度，本文使用归一化相关系数(normalized correlation coefficient，NC)来表示，即

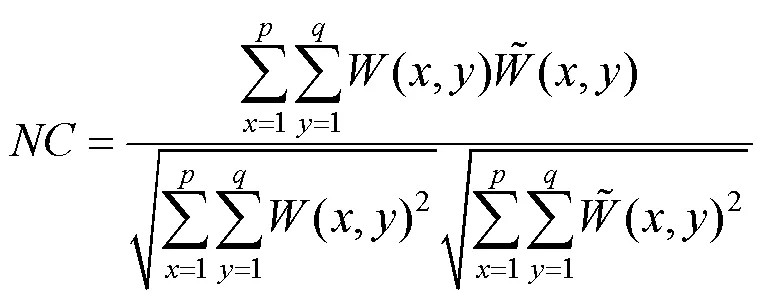
3.2 实验参数

水印嵌入过程中使用的部分实验参数在提取过程也需要用到，这些参数被称之为密钥，包含Arnold变换置乱次数和水印嵌入强度。本文将Arnold变换置乱次数值设定为5。随着水印信息嵌入强度的增加，提取水印的NC值越大，鲁棒性越高，但对宿主图像造成的损害也会变大，PSNR数值也会因此降低。本文选择嵌入强度为1=0.04，2=0.02，3=0.02，4=0.02，5=0.05。此外还设置了=0.2的BEMD分解筛分的终止条件，该条件决定了IMF数量和计算时长。

3.3 实验结果

在实验中，使用了5种不同纹理程度的宿主图像，分别是Peppers，Lena，Barbara，House和Mandrill的灰度图像，大小均为512×512(图3)。其中，Peppers图像纹理相对较差且含有大量平滑区域；Lena图像是一张在特定区域纹理丰富的图像；Barbara图像纹理相对丰富，且纹理分布区域不集中；House图像纹理相对丰富且相对集中；Mandrill图像是一张整体纹理非常丰富的图像。使用的水印图像分别是小熊灰度图像、圣诞树灰度图像和猫爪灰度图像，大小均为64×64。为了能够展示本文算法在不可见性和鲁棒性方面的效果，分别进行了不可见性实验和鲁棒性实验。

图3 不可见性实验结果((a)原始图像；(b)嵌入水印后的图像；(c)提取水印)

3.3.1 不可见性实验

图3展示了本文算法对5种宿主图像在嵌入水印后的不可见性结果。通过嵌入不同灰度水印图像，宿主图像PSNR值在43 dB左右，具有良好的不可见性。此外，嵌入相同水印时纹理复杂的图像具有更加优异的掩蔽性。因此，纹理复杂程度越高，宿主图像的PSNR值更高，不可见性更优越。本文通过精确的数据评估，提取的水印图像与原始水印图像完全一致。

3.3.2 鲁棒性实验

表1为不同宿主图像面对各种攻击时提取水印图像的NC值，结果显示提取水印NC值上下波动较小。在大比例裁剪、椒盐噪声、缩放、滤波攻击下提取的水印图像NC值均在0.98以上，且8种常见攻击的NC均值在0.95以上。通过图4可以看出，随着攻击强度的增加提取水印的NC值逐渐降低。在面对20%的椒盐噪声、15°旋转、40% JPEG压缩、[6, 6]中值滤波高强度攻击时，本文算法提取的NC值仍然在0.9以上，具有较强的鲁棒性。此外，本文还选取了噪声、裁剪、压缩、滤波4种不同类型的攻击进行不同参数的实验来验证算法的鲁棒性，并展示了面对各种攻击时宿主图像受到地损害以及提取的水印图像。

图5为Barbara图像分别在2.0%，5.0%，10.0%和20.0%密度的椒盐噪声攻击时的图像以及提取的水印图像。从实验数据可以看出，当椒盐噪声的密度由2.0%提升到20.0%时，提取水印的NC值仅从0.997变为了0.976，下降幅度较小。在视觉效果上，20.0%椒盐噪声攻击下提取的水印图像出现椒盐颗粒，但水印图像整体依然清晰完整。由此可知，本文算法在高密度椒盐噪声攻击下的水印图像依然具有高辨识度。

图6为Barbara图像在受到不同形状裁剪后的图像以及提取的水印图像。在面对左上角34.3%和左下部分50.0%的大比例裁剪攻击时提取的水印图像依然完整，并且NC值在0.997以上。此外对宿主图像的中间部分进行28.8%的花样十字剪切以及33.4%的方形剪切提取的水印NC值均为1。实验结果表明，本文水印算法并未因为裁剪比例的增加和裁剪方法的多样性而出现无法提取水印的情况，相反对大比例裁剪以及复杂裁剪攻击有着很强的鲁棒性。

表1 不同图像受到各种攻击后NC值

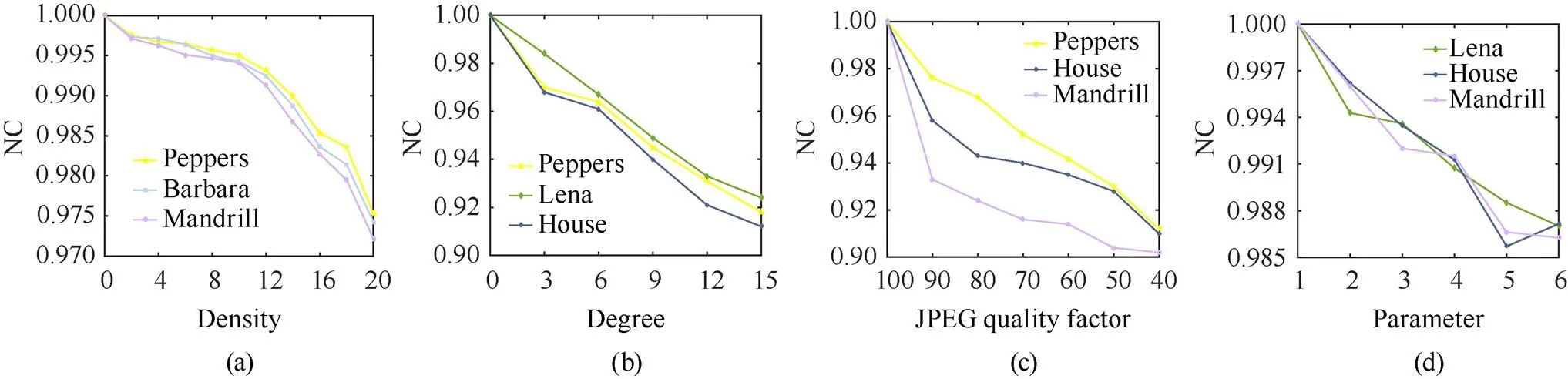
图4 面对不同参数攻击时的折线图((a)椒盐噪声；(b)旋转攻击；(c)JPEG压缩；(d)中值滤波)

图5 椒盐噪声攻击实验结果

图6 裁剪攻击实验结果

图7为Barbara图像受到[2,2]和[3,3]的Wiener滤波，以及[2,2]和[3,3]的均值滤波攻击后的图像和提取的水印图像。滤波属于图像增强技术中的一种，主要用于去除图像噪声，因此对图像影响较小。在[2,2]的滤波攻击后图像的改变较小，在增加到[3,3]强度后图像影响依然较小。另外在图像面对滤波处理后提取的水印NC值均在0.99以上，提取水印清晰，具有较强的鲁棒性。

图8为Barbara图像受到90%，70%，50%和30%压缩攻击后的图像以及提取的水印图像。JPEG压缩攻击常发生在图像传输过程中，通过去除冗杂数据来减少数字产品的比特数。一般压缩算法均是无损压缩，对图像质量影响较小，但在压缩比很高时也会出现压缩失真现象。从图中看出随着压缩比的降低，Barbara图像的纹理细节逐渐丢失，提取的水印图像NC值逐渐降低，但仍在0.93以上。水印图像在面对30%的压缩攻击时图像依然能够清晰分辨出水印图案，具有较高的鲁棒性。

图7 图像滤波实验结果

图8 压缩攻击实验结果

3.3.3 与其他算法的对比

将水印图像分解、分块嵌入到复杂度较高的地方既提高了水印的不可见性又提高了水印的安全性。相对于其他分块方法本文算法利用重复嵌入的方法极大地提高了裁剪攻击的鲁棒性。另外使用投票程序也使鲁棒性有了很大地提高。实验数据表明本文算法对噪声、几何攻击、JPEG压缩、图像增强技术有着良好的鲁棒性。从表2中可以看出，在常见的攻击下本文算法整体优于其他5种算法。面对4大攻击类型时，本文算法中9种攻击提取的NC值在0.9以上，具有良好的鲁棒性。文献[9]算法在面对高斯攻击时具有良好的鲁棒性，但是对椒盐噪声以及3种常见的几何攻击抵抗性较低；文献[10]算法在面对几何攻击及压缩攻击时鲁棒性较低；文献[8]、文献[11]和文献[12]算法在面对部分几何攻击和图像增强技术时鲁棒性较低，其中文献[11]和文献[12]算法的PSNR值较高，具有良好的不可见性。

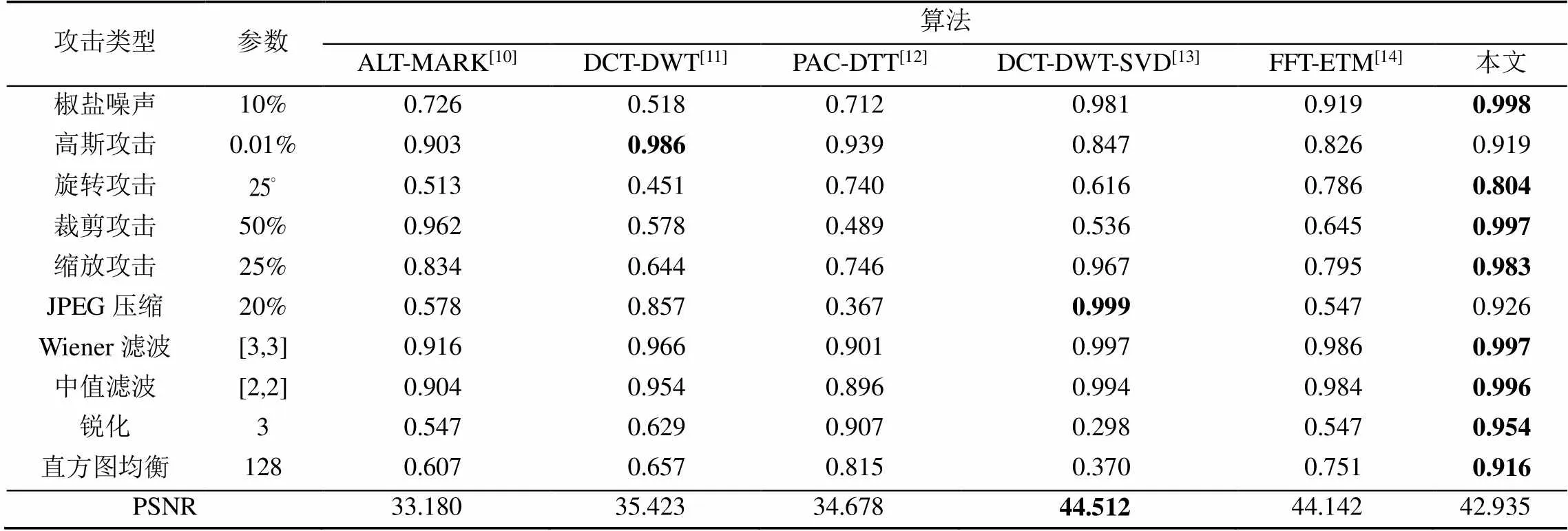
表2 不同算法受到各种攻击后NC值对比

注：加粗数据为最优值

4 结束语

本文提出了一种结合纹理复杂度与经验模态分解的灰度水印图像算法。其主要思想是通过对宿主图像进行纹理复杂度检测，并选择复杂度高的分块位置嵌入水印来提高水印的不可见性。通过评价水印的鲁棒性与不可见性之间的关系，选择将置乱后的水印BEMD分解得到的信息嵌入到宿主图像对应的内蕴模态函数。经过大量实验测试，本文对多种不同类型的攻击具有良好的鲁棒性。通过与其他灰度水印算法对比，本文算法在不可见性和鲁棒性方面整体优于其他对比算法。由于灰度水印图像灰度值比较大且数值复杂，宿主图像在面对整体像素灰度值完全改变时，嵌入系数低的水印信息很容易损失，因此提取出的水印很难完整，未来可以结合其他算法对本文算法进行改进以提高鲁棒性。

[1] BALASAMY K, SUGANYADEVI S. A fuzzy based ROI selection for encryption and watermarking in medical image using DWT and SVD[J]. Multimedia Tools and Applications, 2021, 80(5): 7167-7186.

[2] SUN W W, ZHOU J T, LI Y M, et al. Robust high-capacity watermarking over online social network shared images[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(3): 1208-1221.

[3] 韩绍程, 张鹏. 基于DOCT和SURF的立体图像零水印算法[J]. 图学学报, 2022, 43(2): 254-262.

HAN S C, ZHANG P. Stereo image zero watermarking algorithm based on DOCT and SURF[J]. Journal of Graphics, 2022, 43(2): 254-262 (in Chinese).

[4] 胡海, 李叶凡, 王晗, 等. 基于空间转换网络的视频盲水印方法[J]. 图学学报, 2020, 41(5): 757-763.

HU H, LI Y F, WANG H, et al. Video blind watermarking via spatial transformer networks[J]. Journal of Graphics, 2020, 41(5): 757-763 (in Chinese).

[5] SOWMVA S, KARANTH S, KUMAR S. Protection of data using image watermarking technique[J]. Global Transitions Proceedings, 2021, 2(2): 386-391.

[6] BENDER W, GRUHL D, MORIMOTO N, et al. Techniques for data hiding[J]. IBM Systems Journal, 35(3.4): 313-336.

[7] SHARMA S, SHARMA H, SHARMA J B. Artificial bee colony based perceptually tuned blind color image watermarking in hybrid LWT-DCT domain[J]. Multimedia Tools and Applications, 2021, 80(12): 18753-18785.

[8] ALTAY Ş Y, ULUTAŞ G. Self-adaptive step firefly algorithm based robust watermarking method in DWT-SVD domain[J]. Multimedia Tools and Applications, 2021, 80(15): 23457-23484.

[9] BEGUM M, UDDIN M S. Implementation of secured and robust DFT-based image watermark through hybridization with decomposition algorithm[J]. SN Computer Science, 2021, 2(3): 1-13.

[10] ANDALIBI M, CHANDLER D M. Digital image watermarking via adaptive logo texturization[J]. IEEE Transactions on Image Processing, 2015, 24(12): 5060-5073.

[11] ABDULRAHMAN A K, OZTURK S. A novel hybrid DCT and DWT based robust watermarking algorithm for color images[J]. Multimedia Tools and Applications, 2019, 78(12): 17027-17049.

[12] KHAN A. PCA-DTT 2D-DHCES based attack resilient imperceptible image watermarking[J]. Multimedia Tools and Applications, 2021, 80(5): 7515-7527.

[13] ZHANG L N, WEI D Y. Dual DCT-DWT-SVD digital watermarking algorithm based on particle swarm optimization[J].Multimedia Tools and Applications, 2019, 78(19): 28003-28023.

[14] KHAN A, SARFARAZ A. FFT-ETM based distortion less and high payload image steganography[J]. Multimedia Tools and Applications, 2019, 78(18): 25999-26022.

[15] NUNES J C, BOUAOUNE Y, DELECHELLE E, et al. Image analysis by bi-dimensional empirical mode decomposition[J]. Image and Vision Computing, 2003, 21(12): 1019-1026.

[16] 赵松杰, 张亚博, 宣龙健. 基于BEMD和DCT的图像数字水印算法[J]. 现代电子技术, 2013, 36(17): 59-61, 64.

ZHAO S J, ZHANG Y B, XUAN L J. Image digital watermark algorithm based on BEMD and DCT[J]. Modern Electronics Technique, 2013, 36(17): 59-61, 64 (in Chinese).

[17] 李小满, 李峰, 章登勇. 基于二维经验模式分解的图像水印嵌入算法[J]. 计算机工程, 2011, 37(12): 119-121.

LI X M, LI F, ZHANG D Y. Image watermark embedding algorithm based on bidimensional empirical mode decomposition[J]. Computer Engineering, 2011, 37(12): 119-121 (in Chinese).

[18] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995.

[19] ZHU P, LIU L, ZHOU X L. Infrared polarization and intensity image fusion based on bivariate BEMD and sparse representation[J]. Multimedia Tools and Applications, 2021, 80(3): 4455-4471.

[20] DI C L, YANG X H, WANG X C. A four-stage hybrid model for hydrological time series forecasting[J]. PLoS One, 2014, 9(8): e104663.

[21] WANG X C, HU J P, GUO L X, et al. Feature-preserving, mesh-free empirical mode decomposition for point clouds and its applications[J]. Computer Aided Geometric Design, 2018, 59: 1-16.

[22] 丁玮, 闫伟齐, 齐东旭. 基于Arnold变换的数字图像置乱技术[J]. 计算机辅助设计与图形学学报, 2001, 13(4): 338-341.

DING W, YAN W Q, QI D X. Digital image scrambling technology based on Arnold transformation[J]. Journal of Computer Aided Design & Computer Graphics, 2001, 13(4): 338-341 (in Chinese).

Grayscale watermarking algorithm via BEMD and texture complexity

ZHAO Hui-chao1, HU Kun2, WANG Xiao-chao1

(1. School of Mathematical Sciences, Tiangong University, Tianjin 300387, China;2. Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100049, China)

This paper presented a grayscale watermarking algorithm combining texture complexity and bi-dimensional empirical mode decomposition (BEMD). Firstly, the watermark image after Arnold transform was decomposed by BEMD to obtain the intrinsic modal function (IMF) and the residual information of different scales. Then, the texture complexity of the host image after segmentation was calculated, and the region of high texture complexity was selected as the embedding location. In order to better fuse the IMF of the watermark image with the host image, BEMD decomposition was performed on the host image under the same sieving conditions as those for the watermark image. Finally, the watermark information was repeatedly embedded into the pre-selected location of the host image, and then the image embedded with watermarks was reconstructed by the IMF and the residual. Watermark extraction was the inverse process of watermark embedding. The experiments on host images at different texture levels revealed that the peak signal-to-noise ratios of images embedded with watermarks were all above 40 dB, and the normalized coefficients values of watermark extraction all exceeded 0.95 in the face of eight common attacks. Compared with the existing algorithms, the proposed algorithm performs well in large scale shearing, noise attack, image filtering, and JPEG compression attack, superior to the algorithms under comparison.

bi-dimensional empirical mode decomposition; grayscale watermarking; texture complexity;copyright protection;Arnold transform

14 October，2021；

The Science & Technology Development Fund of Tianjin Education Commission for Higher Education (2018KJ222); Open Project Program of the State Key Lab of CAD&CG, Zhejiang University (A2105)

ZHAO Hui-chao (1997-), master student. Her main research interest covers digital image processing. E-mail：zhaohuichao1111@163.com

TP 391

10.11996/JG.j.2095-302X.2022040659

A

2095-302X(2022)04-0659-08

2021-10-14；

2022-04-15

15 April，2022

天津市高等学校基本科研业务费项目(2018KJ222)；浙江大学CAD&CG国家重点实验室开放课题(A2105)

赵慧超(1997-)，女，硕士研究生。主要研究方向为数字图像处理。E-mail：zhaohuichao1111@163.com

王小超(1987-)，男，副教授，博士。主要研究方向为图形图像处理、计算几何等。E-mail：wangxiaochao18@163.com

WANG Xiao-chao (1987-), associate professor, Ph.D. His main research interests cover graphic image processing, computation geometry, etc. E-mail：wangxiaochao18@163.com