基于虚拟光源的实时半透明材质渲染
陈主昕,杨沁七,陈 瑞,张严辞,刘艳丽,吴志红
基于虚拟光源的实时半透明材质渲染
陈主昕,杨沁七,陈 瑞,张严辞,刘艳丽,吴志红
(四川大学计算机学院,四川 成都 610065)
半透明材质渲染是实时渲染领域的重要研究部分。针对透射渲染依赖于准确的透射厚度计算,往往受限于场景模型和光照的复杂度问题,提出一种基于虚拟光源来计算半透明材质渲染中的透射厚度的方法。即在场景中增加一个虚拟光源,并在虚拟光源处使用排序算法来计算场景的深度信息。在计算从真实光源到着色点处的透射厚度时,提出在两者世界空间连线的直线段上进行采样,统计在物体内部的采样点占总采样点数目的比例,乘以直线段的长度得到估计结果。并且,当场景中存在多个真实光源时,基于采样的方法能够复用虚拟光源中存储的场景深度信息。该算法能够有效地提升透射厚度计算的准确率,也能减轻场景中光源数量增多带来的显存开销问题。实验证明该方法能在效率、效果和显存开销之间取得较好的平衡。
半透明材质渲染;透射厚度;虚拟光源;排序算法;多光源
次表面散射是生活中常见的现象,也是真实感渲染中不可缺少的部分。能够发生次表面散射的物体,如皮肤、蜡烛、玉石、牛奶等,在渲染中均被称为半透明材质。由于光线在进入这些物体内部,并经过一定的反射与折射之后会从另一个点射出,在视觉上就会给人一种柔和与饱满的感觉。其中,在比较薄的部分,光线会穿透物体,呈现出剔透感,这种情况又被特化为透射现象。
为了渲染出较为真实的透射效果,许多高精度的模型被用于模拟光线在物体内部的散射路径[1-3]。为了加速散射计算,STAM[4]提出了扩散理论,后人在此基础上提出了许多模拟散射的方法,其在提高计算效率的同时也能渲染出比较真实的结果。
透射属于广义上的次表面散射,但却特指光线从入射点的异侧出射的情况。根据这个特性,就有许多通过估计透射厚度来渲染半透明材质的方法[5-6]。其中最重要的是能准确地计算光源到达着色点的透射厚度。但现有的透射厚度计算方法[5]需同时满足3个条件才能保证计算的正确性:①场景中均为闭合规整的物体;②忽略光线与物体表面相切的情况;③光源与相机均处于物体外部。
但对于复杂的场景而言,要完全满足以上3个条件非常困难。另外,复杂场景中通常存在成百上千的光源,现有的方法由于需要在每个光源处保存完整的场景信息,会很快耗尽显存。于是本文基于射线法的基本原理提出虚拟光源算法,通过采样的方式提高透射厚度计算的准确度。基于虚拟光源,能在提高算法准确率和效率的同时,显著减少显存的消耗。
1 相关工作
半透明物体的离线渲染算法主要是通过辐射传输方程[7]结合多分层的蒙特卡洛(Monte Carlo multi-layered,MCML)[8]方法求解光线在物体内部的散射结果。暴力路径追踪[1]方法、体积路径追 踪[2]方法和体积光子映射[3]方法均是基于该思路提出的算法。文献[4]以光线的散射距离为自变量函数来近似能量的衰减,并提出了扩散(Diffusion)理论。基于此理论,JENSEN等[9]在双向反射分布函数(bidirectional reflectance distribution function,BRDF)[10]方程的基础上提出了双向次表面反射分布函数(bidirectional scattering-surface reflectance distribution function,BSSRDF)方程以精确描述次表面散射现象,并使用扩散剖面(diffusion profile)曲线来描述多种不同的材质。同时,为了加速多重散射的计算,还利用偶极子(dipole)模型来高效地计算扩散剖面。DONNER和JENSEN[11]将光子映射引入扩散剖面的计算,从而提升了散射计算的准确性。HABEL等[12]将蒙特卡洛重要性采样应用到光子映射模拟次表面散射的领域,使得该方法能够处理任意方向的入射光。
实时次表面散射算法的基本思想也是来自于文献[9]引入的扩散剖面曲线,并使用一些方法来近似计算光在特定材质中散射后的衰减。第一类方法是表面泼溅(surface splatting),其通过splat多边形来计算领域内片段的散射贡献[13-14]。另一类方法是使用多个高斯函数加权来近似扩散剖面[15-17]。文献[18-19]基于屏幕空间滤波的方法,提高了绘制多个半透明物体的效率。YATAGAWA等[20]利用线性分解来支持各向异性材质的散射。XIE等[21]则在此基础上利用时间方差进一步提升了渲染效果。
实时透射算法在大多数情况下均使用实时次表面散射算法来计算,这是因为其在物体内部的扩散过程非常相似,但也有一些针对透射渲染的算法。文献[6]扩展了传统的阴影贴图来进行透射颜色的计算。JIMENEZ等[22]为了渲染皮肤的透射效果,对透明阴影贴图进行了一定的简化。MAISCH和ROPINSKI[23]提出了基于空间邻接图的方法,使透射渲染可以应用于区域光源与环境光源的场景。同时,也有许多研究聚焦于透射物体厚度的计算[24-26]。GOLUBEV[27]提出根据场景的条件自适应地选择不同的透射距离计算方法,实现了更高质量的透射效果。文献[5]使用模块化技术加速厚度计算,以提高计算的效率。
片元排序技术分为3类:①深度剥离[28],通过多次光栅化场景来获取多个深度层次的片段;②A-buffer[29],为了减少多次光栅化场景带来的开销,提出使用特定的数据结构并结合一次光栅化操作来保存所有片段的深度;③K-buffer[30],核心思想是通过一次场景的光栅化在每一个像素位置保存个最重要的片段,再对这个片段进行排序,进一步提高了计算效率并减少了存储开销。
2 算法概述
在渲染场景中,计算半透明物体的透射颜色时,最常使用的方法是BSSRDF,即
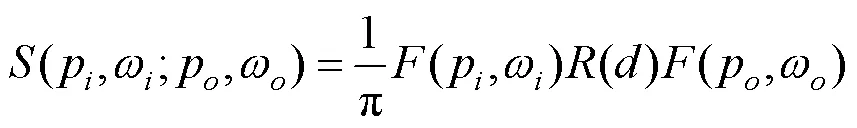
其中,p和ω分别为光线的入射点和方向;p和ω为光线的出射点和方向;为透射距离;(,)为菲涅尔函数;()为光线从入射点到出射点的衰减。要真实地渲染出半透明物体,快速并准确地计算()是关键的一步。在实时渲染中,常使用个高斯函数来近似物理真实的(),即

其中,为高斯函数;权重w和方差v与具体的物体材质相关。虽然使用该方式可以提高计算的效率,但是透射距离的计算却受到准确性和存储开销的限制。
针对以上问题,本文提出了基于虚拟光源的实时半透明材质渲染算法,通过在场景中增加一个虚拟光源来计算透射厚度。基本思想是在虚拟光源处使用片元排序算法对场景的深度进行排序并保存,在计算真实光源到着色点的透射厚度时,在透射光线上采样并映射回虚拟光源处进行判断,根据采样点在物体内部的比例对透射厚度进行估算。这样既可以提高透射厚度估算的准确性,也能减少多光源场景中每一个真实光源均需保存场景深度的开销。
3 计算透射厚度
在图1的场景中,红色箭头表示的透射光线不满足光线不与物体表面相切的条件,使得计算得到的透射厚度偏差严重。本节要解决的问题就是如何基于虚拟光源来计算透射厚度并不受场景复杂度的限制。

图1 透射厚度计算示例场景
3.1 采样透射厚度
透射厚度的计算目标是准确地求解光源到着色点所经过物体内部的距离总和。如,在计算图1中从光源到着色点处的透射厚度,就是求解线段上属于物体内部的长度和。基于此,本文提出通过采样的方式来近似计算透射厚度。最简单的方法就是在线段上均匀地分布采样点(图1中橙色小点),然后通过判断处于物体内部的采样点占总采样点的比例,再结合线段的长度就可以估计透射厚度,即
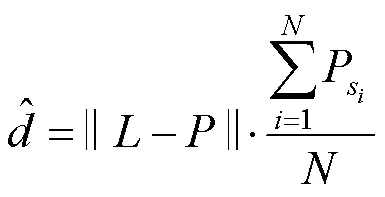
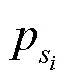

由于不使用透射光线与物体的交点来估计透射厚度,就不会将着色点误判为处于物体外部,所以能够减少由物体不规整或光线与物体相切带来的计算误差。
3.2 采样点判断
为了能够高效地判断采样点是否在物体内部,在场景中增加一个虚拟光源ʹ,并从所有的采样点出发向ʹ发出射线(图1中黄色虚线箭头所示)。最后根据几何射线法可判断采样点s是否处于物体内部,即从采样点出发,向着虚拟光源ʹ发射一条射线,若该射线在到达光源位置前与物体相交的次数为奇数,那么该点在物体内部,否则在物体外部。由于采样点之间互不相关,即使光线与物体相切导致判断错误,也不会造成巨大的计算误差。
在计算交点数目时,将采样点s投影到虚拟光源ʹ的空间,并计算其相对于虚拟光源ʹ的深度值。此时,由于已经在虚拟光源ʹ处对场景进行排序并保存了深度信息,所以就能基于像素链表方法[5]计算出采样点s对应的小于其深度的片元数量。其得到的数量就是从采样点s到虚拟光源ʹ之间与物体的交点数目。
4 选择最佳虚拟光源
基于已提出的虚拟光源,便可非常容易地扩展到多光源的场景,并且不需要像文献[5]一样对每个真实光源都绘制一遍场景。但由于场景中的每个真实光源均需复用虚拟光源中保存的场景深度信息,所以需解决的问题就是如何选择一个最佳的虚拟光源朝向,并设定好最佳的投影矩阵与位置来获得更好的效果与更快的效率。
4.1 求解虚拟光源投影矩阵
在保存深度信息的纹理分辨率固定的条件下,虚拟光源的可视范围越小,保存在深度纹理中片元的深度值精度就越高。那么最精确的虚拟光源可视范围就是相机的可视范围,但会丢失许多相机之外的半透明片元,导致对采样点的判断出现偏差,最后造成透射厚度计算不正确。
因此,虚拟光源的视口范围刚好包裹住所有半透明物体时,其投影矩阵为最佳。一方面,这样的投影矩阵能尽可能地保存对透射厚度计算有影响的片元深度;另一方面,能使得片元保存的深度值具有较高的精度。
算法1为求解虚拟光源位置和投影矩阵的方法,通过求解能包裹所有半透明物体的包围盒来计算虚拟光源的视口范围。首先,计算所有半透明物体的包围盒,取,,3个轴向上的最大、最小值作为场景的包围盒。然后生成片元总数图,通过片元总数图来确定虚拟光源的朝向(见4.2节)。接下来从场景包围盒的中心,沿着虚拟光源朝向的反方向,由给定的距离参数确定虚拟光源的位置。最后将场景包围盒的8个顶点变换到虚拟光源空间下,求解出变换后的坐标在,,3个轴上的最值作为虚拟光源投影矩阵的参数。
算法1.计算虚拟光源的位置和投影矩阵
输入:所有的半透明物体,距离参数以及待定的虚拟光源视口朝向。
输出:虚拟光源位置和投影矩阵。
// 计算包裹住所有半透明物体的最小场景AABB
1. aabbInScene ← 0;
2. for obj ∈do
3. aabbOfObj ← calculateAABB(obj);
4. aabbInScene ← mixAABB(aabbIns -cene, aabbOfObj);
// 确定虚拟光源的最佳视口朝向
5. l ← calculateMaxEdgeLengthOfAABB (aabbInScene);
6. d ← 0;
7. maxW ← 0;
8. for dir ∈. do
9. fragmentNumMap ← generateFrag -mentNumMap (, l,,);
10. w ← calculateMapWeight(fragm -entNumMap);
11. if w > maxW then
12. maxW ← w;
13. d ← dir;
//计算虚拟光源的位置
14. center ← calculateAABBCenter(aabb -InScene);
15.← center – l d;
16. params ← transformAABB(aabbInS -cene,, d);
//计算虚拟光源的投影矩阵
17.← perspective(params);
18. return,;
由此,计算得到的虚拟光源的投影矩阵为

其中,m=min,m=max,m=min,m=max,m=(-)min,m=(-)max。距离参数通过影响投影矩阵来影响渲染,并统一将其设置为=0.8。
4.2 选择虚拟光源朝向
即使计算的投影矩阵均能包裹住半透明物体,但不同朝向的虚拟光源所生成的深度信息纹理会有很大的差别,最后在计算透射厚度时的效果和效率会有较大的区别。这是因为在不同的朝向下,场景投影到虚拟光源的屏幕空间中所占的比例不同,每一个像素所包含的片元数量也不同,导致了深度信息的精确度有所区别。并且,在确定虚拟光源的朝向时,还需考虑光线相切或模型的不规范导致的采样点内外判断错误的问题。
为了解决这些问题,本文使用片元总数图来辅助计算虚拟光源的朝向。即通过计算半透明物体与每条光线相交的片元总数来生成片元总数图。若片元总数图中某个纹素值为奇数,则说明该光线出现了相切或模型不规整问题。且片元总数图中拥有片元的像素平均片元层数越少,计算效率则越高。也就是说,越好的虚拟光源朝向,在生成的片元总数图中,拥有片元的像素占比越大,拥有片元的像素中平均片元数越少。所以,在选择虚拟光源的最佳朝向时,需基于片元总数图来计算一个权重,将最高权重的片元总数图所对应的朝向视为最佳的结果,即

其中,k为片元总数图中片元数不为0的像素的比例;k为片元总数为奇数的比例;k,min和max分别为所有像素片元层数的平均值、最小值和最大值;,,分别为不同比例所占的权重,且权重与场景相关。当虚拟光源朝向与视线接近平行时,光线相切或模型不规整问题就会被放大,此时需增加的值。如果场景中的光源过多,对算法效率有较大影响时,就应降低的值,通过牺牲一些准确性来提高计算效率。
为了提高计算效率,本文预设6个虚拟光源的朝向,并只在初始化阶段计算所有朝向的片元总数图,以此选择一个最佳朝向。之后,只在最佳朝向下生成片元总数图并计算权重,且当下降到初始值的一半以下时,才全部重新计算并选择最佳朝向。
5 优化采样效率
在使用虚拟光源算法计算透射厚度时,在每一条透射光线上均需做均匀采样,且每一个采样点均要借助场景深度纹理来判断是否在物体内部。那么采样点的数量就直接影响到了透射厚度计算的准确率和效率。如何在保证渲染质量同时,通过减少采样点数量来提高计算效率是需要解决的问题。
5.1 自适应步长采样
以第3节从真实光源采样算法出发,根据固定的采样步长向着色点前进。因此,采样步长就决定了采样点的数量。如果增大采样步长,就能够减少采样的总数从而提高算法效率。本文使用的自适应采样方式需要设置最小及最大的采样步长min和max,初始时从最小采样步长开始。如果相邻两次采样的点均在物体外部或内部,那么下一次进行采样时就需扩大采样步长,反之则缩小采样步长,即

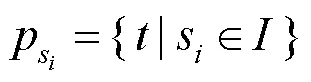
同时,式(3)对透射厚度的估计修改为步长之和,即

再结合文献[22]提出的近似方法,可快速地估算出
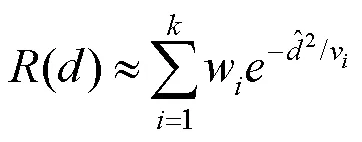
5.2 空间跳跃
要在不影响采样效果的基础上提高采样效率,除了自适应地调整步长之外,还可通过将采样点限制在有效采样的范围之内。第3节的采样是在整条透射光线上进行的,但透射光线在传输过程中并不完全处于物体内部,有某段光线处于物体外部,对其进行采样就是无效的,所以需利用空间跳跃的思想来限制采样范围。空间跳跃法是体渲染领域常用的方法之一,本文受稀疏跳跃法[31]启发,在真实光源处对场景进行光栅化,以得到的深度信息进行空间跳跃并辅助采样。
(1) 深度图信息辅助采样。在渲染场景中,某些光源会位于距离半透明物体较远的位置,这些光源到半透明物体的入射点之间的空间,就是无效的空间。因此,将采样的范围限制在光线的入射点到着色点之间,就可以极大地提高采样效率。真实光源到半透明物体的入射点可以通过深度图得到,在后续计算透射厚度时,只需要将深度图与光源的投影矩阵、视图矩阵相结合,就可以反推出这条透射光线的入射点,并将其作为采样起点,便可跳过这段无效的空间。同时,真实光源的深度图不仅可以用于空间跳跃,还可以用于计算不透明物体的阴影,所以这个方法不会增加计算和存储的开销。
(2) 片元总数图信息辅助采样。对于许多透射光线而言,其所穿透的半透明物体的路径是完全实心的。意味着这些透射光线只会进入半透明物体一次,并且从半透明物体出射后就不再与任何半透明物体相交。透射光线是否透过实心的半透明段,可以借助片元总数图来进行判断。本文通过在每一个真实光源处保存一张片元总数图来辅助计算,在对透射光线进行采样之前,先判断片元总数图中其对应的值是否为2,如果为2就代表这条透射光线经过的半透明路径是完全实心的,即可跳过这部分采样直接进行计算。
6 实验结果
本文在多个场景中设置不同的光源和视点进行实验,并对提出的基于虚拟光源的透射厚度计算方法以及采样效率的优化方法进行了分析验证。实验环境为:Intel Core i5-8400 CPU、NVIDIA GeForce GTX 1060 GPU、8 GB内存。基于G3D Engine[32]实现了本文算法及对比算法对比,渲染结果的分辨率和场景深度纹理的分辨率分别为1920×1080和1024×1024。
图2分别显示了本文方法对4种半透明模型的渲染结果,可以看到该方法生成了比较真实的透射效果。为了说明本文方法的有效性,实现了深度图法[6]和模块链表法[5]对半透明材质的渲染,并与本文虚拟光源法进行比较分析。此外,使用路径追踪所计算的透射厚度结果作为Ground Truth。
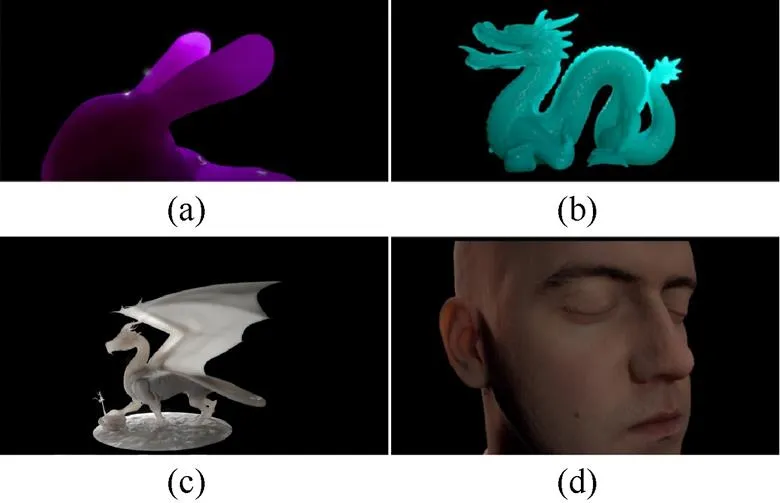
图2 不同半透明材质模型的渲染结果((a)兔子模型;(b)龙模型;(c)飞龙模型;(d)人脸模型)
在图1所示的场景中,从不同视点分别使用这3种算法计算场景中每个片元对应的透射厚度,并与路径追踪的结果进行比较。并使用均方根误差(root mean square error,RMSE)表示,以此来验证本文算法在复杂场景中计算的半透明物体透射厚度的准确性。
图3可视化了这3种算法计算得到的每一个片元的误差率和RMSE (黄色表示高误差,蓝色表示低误差)。可以看到本文算法在大多数情况下计算的透射厚度误差均小于深度图法和模块链表法。这是因为深度图法,只计算透射光线的入射点与着色点之间的距离,当透射光线经过的透射路径中存在外部空间,就会产生极大的误差。对于模块链表法,在片元法线与光线入射方向接近垂直时,由于深度信息采样误差和光线与片元相切误差导致厚度计算误差较大,所以在视点2和3处产生误差和RMSE均大于本文算法。然而,在视点1处,本文算法计算的透射厚度准确率比模块链表法低,是因为在该视点处绝大多数透射光线与片元法线均不垂直,从而避免了模块链表法误差较大的情况,由此得到的透射厚度就比通过采样估计得到的结果更加准确。

图3 不同视点下3种算法的厚度计算误差对比((a)深度图法;(b)模块链表法;(c)虚拟光源)
所以,本文所提出的虚拟光源算法在凹型和多层半透明物体的透射厚度计算中,准确度在大多情况下均大于深度图法和模块链表法,且该方法能够显著地降低由模型不规整和光线相切问题造成的计算误差。
为了验证本文算法在透射效果渲染上的优势,选择了图2(c)中的飞龙模型并在3个视图方位下对该模型进行半透明渲染,同时与深度图法、模块链表法的渲染结果进行比较。从图4中可以看到,本文方法具有更高的真实感。这是因为深度图法会错误地计算2个翅膀之间的透射厚度,造成翅膀的透射厚度过大,导致其几乎无透射效果。对于模块链表法而言,3个视图方位下均有比较明显的瑕疵,线框标示出了由于光线相切问题导致厚度计算误差所造成的渲染走样。
同时,还比较了3种算法在单光源场景中渲染飞龙模型的效率,如图4中右上角数字所示(图中差异较大的部分用线框标识,右下角红框为放大的细节,右上角数字表示帧率)。本文的虚拟光源算法在该场景中的效率均比其他2种算法低。这是因为深度图法只需要计算深度图就可进行半透明渲染,而本文算法和模块链表法均需对片元的深度信息进行排序。另外,在单光源场景中,本文算法相比于模块链表法,还需要进行额外的采样操作,从而进一步降低了本文算法的计算效率。
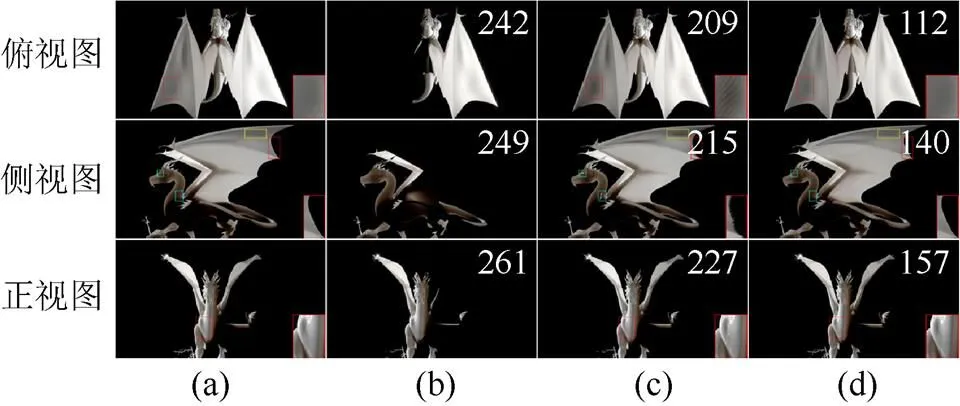
图4 单光源场景中3种算法在飞龙模型不同视图方位下的渲染结果对比((a)Groung Truth;(b)深度图法;(c)模块链表法;(d)虚拟光源)
因此,为了验证本文的虚拟光源算法在多光源场景下的显存和效率优势,同样选择了图2(c)中的飞龙模型进行实验,并将场景深度纹理的分辨率提高4倍,用于模拟显存开销较大的情况,实验结果见表1。在真实光源只有一个的高显存场景中,模块链表法的帧率是本文算法的220%,这是因为本文算法需要进行额外的采样操作,导致效率降低。但模块链表法所需要的显存随着光源数量的增多呈线性增长,当光源数量为10时,由于所需要的总显存量超过了GPU显存的最大值,数据将转存到内存中,使得帧率急剧下降。虽然本文的虚拟光源算法效率均比深度图法低,但能在保证实时的条件下极大地改善渲染效果。
综上所述,相比于深度图法和模块链表法,本文的虚拟光源法能在效率、效果和存储开销之间取得更好的平衡。
最后,为了验证本文方法的有效性,分别对比了在不同场景及采样方法下所需的显存、RMSE和帧率,结果见表2。从误差上分析,空间跳跃法的RMSE值最高,这说明在使用真实光源的深度图和片元总数图来进行空间跳跃时,由于这些辅助图均存在一定的误差,从而增大了渲染结果的误差。从显存开销上分析,空间跳跃法需要额外的显存来增加采样效率,而自适应采样方法与原始采样方法相比不需要额外的显存开销。从帧率上分析,两类采样效率优化方法均能够在一定程度上提高帧率。所以,本文提出的采样效率优化方法虽各有优劣,但至少能提升60%的效率,并且不会带来超过0.02的RMSE值,即在不造成较大精度损失的情况下均能大幅度地提升原始采样的效率。
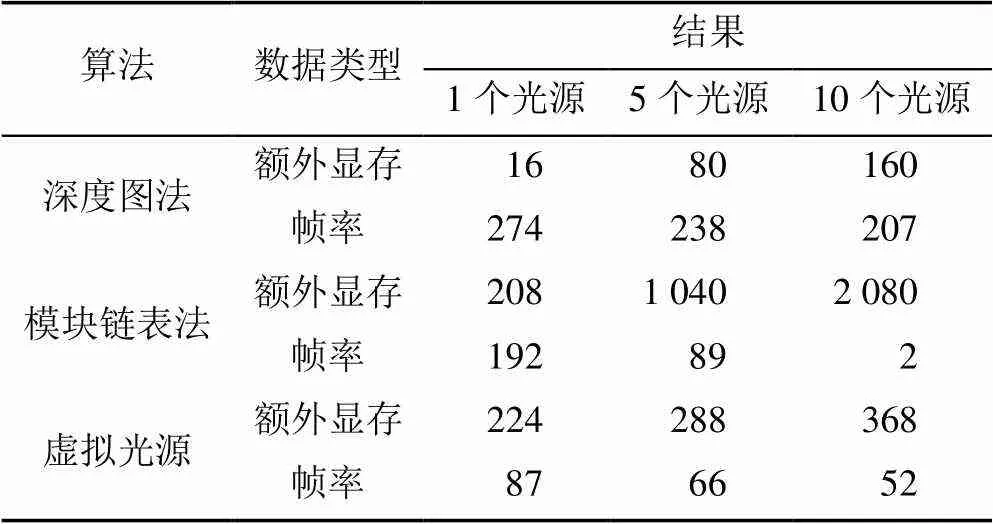
表1 3种算法在高显存场景的显存(MB)与帧率(FPS)

表2 3种采样方法在各种场景渲染中的显存(MB)、RMSE和帧率(FPS)
7 总结与展望
本文提出了一种基于虚拟光源进行透射厚度计算的方法,能够在多光源场景中实现高质量的半透明材质的透射渲染。并通过在场景中增设一个虚拟光源来提高透射厚度计算的准确性并减少在多光源条件下的显存开销和计算开销。为了进一步地提升效果和效率,本文设计了一种自适应的方法来确定虚拟光源的参数并提出了2种优化采样效率的方案。虽然本文方法能在实时的条件下渲染出高质量的半透明效果,但却存在一些需要解决的限制:
(1) 本文所设计的虚拟光源朝向选择方案只能从几个待定朝向中选择一个局部最优的结果。如何在不预设待定朝向的情况下,计算出一个全局最优的虚拟光源朝向,同时保证算法的计算效率,是未来工作的主要方向。
(2) 本文的透射厚度计算方法隐形地假设了所有的半透明物体是各项同性的,即物体内部的密度一致。因此,只需要使用采样点的位置信息即可满足需求。如何利用更多信息使得基于虚拟光源的半透明材质渲染算法支持各向异性的材质,也是未来工作的重要研究方向。
[1] KAJIYA J T. The rendering equation[C]//The 13th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1986: 143-150.
[2] LAFORTUNE E P, WILLEMS Y D. Rendering participating media with bidirectional path tracing[C]//Eurographics Workshop on Rendering Techniques ’96. Vienna: Springer, 1996: 91-100.
[3] JENSEN H W, CHRISTENSEN P H. Efficient simulation of light transport in scenes with participating media using photon maps[C]//The 25th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1998: 311-320.
[4] STAM J. Multiple scattering as a diffusion process[C]// Eurographics Workshop on Rendering Techniques’95. Vienna: Springer, 1995: 41-50.
[5] ARCHER J, LEACH G. Further improvements to OIT sort performance[C]//2018 Computer Graphics International. New York: ACM Press, 2018: 147-152.
[6] DACHSBACHER C, STAMMINGER M. Translucent shadow maps[C]//The 14th Eurographics Workshop on Rendering, New York: ACM Press, 2003: 197-201.
[7] CHANDRASEKHAR S. Radiative transfer[EB/OL]. [2022- 01-05]. https://www.doc88.com/p-74987094240002.html.
[8] WANG L H, JACQUES S L. Monte Carlo modeling of light transport in multi-layered tissues in standard C[R]. San Antoni: The University of Texas, 1992: 1-167.
[9] JENSEN H W, MARSCHNER S R, LEVOY M, et al. A practical model for subsurface light transport[C]//The 28th Annual Conference on Computer Graphics and Interactive Techniques. New York: IEEE Press, 2001: 511-518.
[10] NICODEMUS F E, RICHMOND J C, HSIA J J, et al. Geometrical considerations and nomenclature for reflectance[R]. National Bureau of Standards, 1977.
[11] DONNER C, JENSEN H W. Rendering translucent materials using photon diffusion[C]//ACM SIGGRAPH 2008 Classes. New York: ACM Press, 2008: 1-9.
[12] HABEL R, CHRISTENSEN P H, JAROSZ W. Photon beam diffusion: a hybrid Monte Carlo method for subsurface scattering[J]. Computer Graphics Forum, 2013, 32(4): 27-37.
[13] CHEN G J, PEERS P, ZHANG J W, et al. Real-time rendering of deformable heterogeneous translucent objects using multiresolution splatting[J]. The Visual Computer, 2012, 28(6-8): 701-711.
[14] SHAH M A, KONTTINEN J, PATTANAIK S. Image-space subsurface scattering for interactive rendering of deformable translucent objects[J]. IEEE Computer Graphics and Applications, 2009, 29(1): 66-78.
[15] BORSHUKOV G, LEWIS J P. Realistic human face rendering for “The Matrix Reloaded”[EB/OL]. [2021-07-26]. https://doi.org/10.1145/1198555.1198593.
[16] GREEN S. Real-time approximations to subsurface scattering[J]. GPU Gems, 2004, 1: 263-278.
[17] D’EON E, LUEBKE D. Advanced techniques for realistic real-time skin rendering[EB/OL]. [2022-02-18]. https://www. mendeley.com/catalogue/726e5d2c-a70a-3c7f-bd03-d727ecf32261/.
[18] JIMENEZ J, SUNDSTEDT V, GUTIERREZ D. Screen-space perceptual rendering of human skin[J]. ACM Transactions on Applied Perception, 2009, 6(4): 1-15.
[19] JIMENEZ J, ZSOLNAI K, JARABO A, et al. Separable subsurface scattering[J]. Computer Graphics Forum, 2015, 34(6): 188-197.
[20] YATAGAWA T, YAMAGUCHI Y, MORISHIMA S. LinSSS: linear decomposition of heterogeneous subsurface scattering for real-time screen-space rendering[J]. The Visual Computer, 2020, 36(10-12): 1979-1992.
[21] XIE T T, OLANO M, KARIS B, et al. Real-time subsurface scattering with single pass variance-guided adaptive importance sampling[J]. Proceedings of the ACM on Computer Graphics and Interactive Techniques, 2020, 3(1): 1-21.
[22] JIMENEZ J, WHELAN D, SUNDSTEDT V, et al. Real-time realistic skin translucency[J]. IEEE Computer Graphics and Applications, 2010, 30(4): 32-41.
[23] MAISCH S, ROPINSKI T. Spatial adjacency maps for translucency simulation under general illumination[J]. Computer Graphics Forum, 2017, 36(2): 443-453.
[24] KOSAKA T, HATTORI T, KUBO H, et al. Rapid and authentic rendering of translucent materials using depth-maps from multi-viewpoint[EB/OL]. [2021-08-04]. https://doi.org/10.1145/2407156.2407206.
[25] TOMASZEWSKA A, STEFANOWSKI K. Real-time spherical harmonics based subsurface scattering[C]//Image Analysis and Recognition. Heidelberg: Springer, 2012: 402-409.
[26] JIMENEZ J, ZSOLNAI K, JARABO A, et al. Separable subsurface scattering[J]. Computer Graphics Forum, 2015, 34(6): 188-197.
[27] GOLUBEV E. Efficient screen-space subsurface scattering using burley’s normalized diffusion in real-time[EB/OL]. [2021-08-21]. http://advances.realtimerendering.com/s2018/index.htm.
[28] EVERITT C. Interactive order-independen t transparency [EB/OL]. [2022-01-29]. https://www.mendeley.com/catalogue/1695feca-8162-3679-b67e-95c5aa873834/.
[29] CARPENTER L. The A-buffer, an antialiased hidden surface method[C]//The 11th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1984: 103-108.
[30] BAVOIL L, CALLAHAN S P, LEFOHN A, et al. Multi- fragment effects on the GPU using the-buffer[C]//2007 Symposium on Interactive 3D Graphics and Games. New York: ACM Press, 2007: 97-104.
[31] HADWIGER M, AL-AWAMI A K, BEYER J, et al. SparseLeap: efficient empty space skipping for large-scale volume rendering[J]. IEEE Transactions on Visualization and Computer Graphics, 2018, 24(1): 974-983.
[32] MCGUIRE M, MARA M, MAJERCIK Z. The G3D innovation engine[EB/OL]. [2021-01-07]. https://casual-effects.com/g3d.
Virtual light-based translucent material rendering in real-time
CHEN Zhu-xin, YANG Qin-qi, CHEN Rui, ZHANG Yan-ci, LIU Yan-li, WU Zhi-hong
(Computer Science Department, Sichuan University, Chengdu Sichuan 610065, China)
Translucent material rendering is an essential part of the field of real-time rendering. Transmission rendering relies on the accurate calculation of transmission thickness and is often limited by the complexity of scene models and lighting. This paper proposed a virtual light-based method to calculate the transmission thickness in translucent material rendering. A virtual light was added to the scene, and the sorting algorithm was employed at the virtual light for the depth information of the scene. In calculating the transmission thickness from the real light source to the shading point, it was proposed to take samples on a straight line segment of the world space connecting the two points, calculate the proportion of sampled points inside the object to the total number, which was multiplied by the length of the straight line segment, thus obtaining the estimation. Moreover, in the case of multiple real light sources in the scene, the sampling-based method could reuse the scene depth information stored in the virtual light.The proposed method could effectively enhance the accuracy of transmission thickness calculation, and reduce the memory overhead caused by the increasing number of light sources. Experiments show that the proposed method can strike a good balance between efficiency, effectiveness, and memory overhead.
translucent material rendering; transmission thickness; virtual light; sorting algorithm; multiple lights
24 November,2021;
National Major Project of China (GJXM92579)
CHEN Zhu-xin (1996-), master student. His main research interests cover computer graphics and virtual reality. E-mail:2019223045135@stu.scu.edu.cn
TP 391
10.11996/JG.j.2095-302X.2022040707
A
2095-302X(2022)04-0707-08
2021-11-24;
2022-03-08
8 March,2022
国家重大项目(GJXM92579)
陈主昕(1996-),男,硕士研究生。主要研究方向为计算机图形学与虚拟现实。E-mail:2019223045135@stu.scu.edu.cn
张严辞(1975-),男,教授,博士。主要研究方向为计算机图形学与虚拟现实等。E-mail:yczhang@scu.edu.cn
ZHANG Yan-ci (1975-), professor, Ph.D. His main research interests cover computer graphics, virtual reality, etc. E-mail:yczhang@scu.edu.cn

