基于FPFH特征提取的散乱点云精简算法

李海鹏，徐 丹，付宇婷，柳雁安，张婷婷

基于FPFH特征提取的散乱点云精简算法

李海鹏，徐 丹，付宇婷，柳雁安，张婷婷

(云南大学信息学院，云南 昆明 650500)

针对原始点云模型中存在大量冗余数据问题，提出一种基于快速点特征直方图(FPFH)特征提取的点云精简算法，有效兼顾了特征信息保留和整体完整性。算法首先查找并保留原始模型的边缘点；然后计算非边缘点的FPFH值，由此得到点云的特征值，并进行排序且划分出特征区域和非特征区域，保留特征区域内的点；最后将非特征区域划分为个子区间，对每个子区间用改进的最远点采样算法进行采样。将该算法与最远点采样算法、非均匀网格法、k-means算法和自适应曲率熵算法进行对比实验，并用标准化信息熵评价方法对精简后的点云进行评价，实验表明其优于其他精简算法。此外，可视化结果也表明，该算法能够在保证精简模型完整性的同时，较好地保留住点云大部分特征信息。

点云精简；快速点特征直方图；最远点采样；边界保留；标准化信息熵

相比于二维图像，点云包含着更多的几何信息，被广泛应用于文物保护、测绘、自动驾驶等领域。随着激光扫描技术的不断发展，点云获取的速度越来越快，数据量也越来越大。点云数据中有着丰富的细节特征，也包含着大量的冗余数据点，如果不进行数据精简预处理，不仅不能给后续的处理和模型重建带来很高的精度和收益，反而会降低数据处理效率。因此，在尽可能保留模型细节特征与保证模型完整无空洞的前提下，对点云数据进行精简处理是必不可少的。

国内外研究学者针对点云精简问题作了很多研究，传统的点云精简算法主要有：随机采样法[1]、均匀网格法[2]、包围盒法[3-4]、非均匀网格法[5]、曲率采样法[6]和最远点采样法(farthest point sampling，FPS)[7]等。其中有代表性的均匀网格法首先查找点云模型的最小包围盒，然后将包围盒划分为一定大小的立方体，计算立方体的中值点，用该中值点来表示落在其内的所有点。该方法采样效率较高，采样点分布均匀，但未考虑点云的特征信息。非均匀网格法是均匀网格法的改进，首先查找点云模型的最小包围盒，然后进行非均匀细化，划分为多个小立方体，并计算其中值点，用以代表包含在其内的所有点。该方法能够在一定程度上保留模型的特征信息，但能够保留的特征信息有限。

近年来，很多学者基于k-means聚类、信息熵等方法进行点云精简处理研究。文献[8-11]均分别基于k-means聚类算法设计了相关的点云精简方法。其基本思想是利用k-means算法对点云进行聚类，然后再对每个簇进行精简，保留特征强度大的点，如文献[8]利用k-means聚类将点云模型划分为多个簇，并计算每个簇中的均方根曲率及均方根曲率平均值，删去低于平均值的曲率点。此类方法对特征点的保留效果较好，但算法的时间复杂度较高，而且对特征强度小的点采样不足，精简后的模型也容易出现一些小的孔洞。WANG等[12]提出一种基于自适应曲率熵的点云简化方法，先按一定比例提取曲率较大的点构造初始点云边界，再使用二分聚类算法对点云进行聚类；然后基于自适应随机算法对每个聚类点云进行初步精简，再计算每个聚类点云的曲率熵，并进行二次精简；最后，将提取到的点云边界和精简后的点云组成最终的精简结果。该算法能够保证模型边缘较为完整，保留较多特征点，但仍易出现孔洞，且计算曲率熵的时间成本较大。ZHANG等[13]定义了3种简化熵：尺度保持熵、轮廓保持熵和曲线保持熵，并根据熵值来进行精简。XUAN等[14]利用法向角度和局部熵来评价点的重要性，通过移除最不重要的点并逐步更新法向量和重要性值来进行点云精简处理。此外，SHOAIB等[15]利用分形气泡算法进行点云简化。QI等[16]采用图信号处理的点云精简算法，较好地保留了特征信息。

传统方法大多更侧重于对整体完整性的处理，计算效率高，但对特征点的保留不足；基于k-means的方法能够较好地保留特征点，但对整体的完整性处理不足，在特征区域附近容易出现许多孔洞，尤其是处理大规模点云时精简效果并不佳，而且计算效率较低。针对上述问题，本文提出了一种基于FPFH特征保持的点云精简算法，首先对点云模型进行边界查找，并保留模型的边界点；对非分界点利用快速点特征直方图进行特征值计算，并进行排序和划分，划分出特征点和非特征点；对非特征点利用改进的最远点采样算法进行采样。

1 本文方法

1.1 边界查找

对点云来说，边界轮廓是非常重要的一类特征。对点云数据进行边界查找和保留就是为了使边缘特征能够得到最大程度地保留，保证边界的完整性。

对点云模型边界的查找，首先要构建k-d树，然后搜索k-d树并寻找邻近点[17]。采用最小二乘法对提取的近邻点进行平面拟合，将邻域点集中的点投影到拟合平面上。再对拟合平面上的投影点进行向量构建，找出2个相邻向量之间的夹角。最后根据夹角的大小确定边界点。k-d树的构建是一个递归的过程，首先计算每个维度的方差，根据方差最大维度的中值将数据划分为2个子集，以该中值为根节点构建出左右子树，重复该过程直至不能划分为止。对于每个采样点，用最近邻搜索算法搜索k-d树，找到该采样点的近邻点。以最小二乘法拟合切平面，并将采样点和近邻点投影到切平面上，以采样点的投影点为起点，近邻点的投影点为终点定义向量，并任选一个向量作为参考向量，将参考向量与切平面法线作外积得到向量，再分别求其他向量与参考向量和向量的夹角，根据这些夹角值求解得到最大夹角，当最大夹角大于角度阈值时即可认为该点为边界点[18]，角度阈值一般取π/2。图1为在不同阈值下兔子模型的边界查找结果。

图1 边界查找示意图(红色点为查找到的边界点)

1.2 快速点特征直方图

点云的曲率和法线可以较好描述点云的几何特征，但仅能表示单点特征，无法从中获取太多信息。相比之下，点特征直方图(point feature histograms，PFH)[19-20]就能较好描述采样点与其邻域内点之间的关系。要得到采样点p的特征直方图，首先要找到该点邻域内的其余点，如图2(a)所示，计算这些点两两之间的关系(图中黑色实线表示所连接的2点需要进行一次法线偏差关系计算)。要计算图2(b)的点p和p，首先以点p的法线作为坐标轴，然后用坐标轴与点p到点p方向的单位向量作外积得到坐标轴，再将坐标轴与作外积得到坐标轴，由此完成以点p为原点定义一个局部坐标系。

将局部坐标系平移到点p，设p的法线与坐标轴的夹角的余弦值为，与点p和p连线的夹角余弦值为，在平面的投影ʹ与坐标轴的夹角为，2点的欧氏距离为，则四元组<,,,>的计算式[21]为

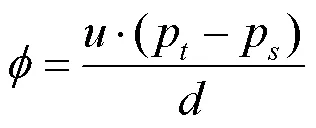
用坐标轴与作内积得到夹角余弦值，用坐标轴与点p到点p方向的单位向量作内积得到夹角余弦值。对于的计算，有如下定义[21]

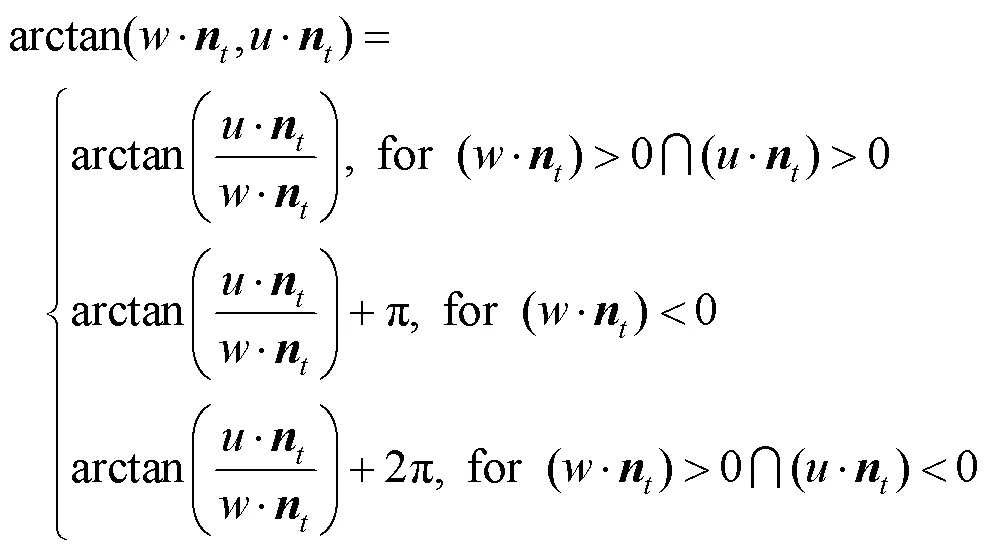
将四元组中的每个特征值都划分成个子区间，统计落在每个子区间内的点的个数并进行归一化处理，即可得到点特征直方图PFH。

由于PFH的时间复杂度为(2)，无法满足实时性要求，RUSU等[22]提出了快速点特征直方图(fast point feature histograms, FPFH)，将时间复杂度降为()。图3为FPFH的计算区域，首先计算点p与其邻域内其他点之间的一个三元组<,,>，将该步计算记为简单点特征直方图(simplified point feature histogram, SPFH)，然后重新确定每个点的邻域，对每个点均计算一次SPFH值，最后根据这些的SPFH值来计算p的FPFH，即

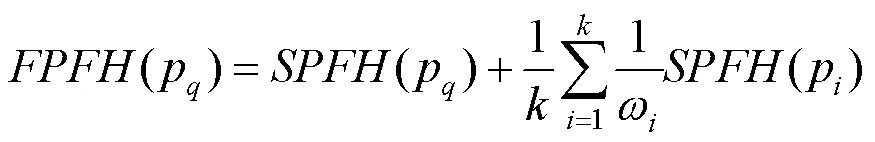
其中，(p)为点p的FPFH值；(p)和(p)分别为点p和p的SPFH值；ω为权重，一般取点p到点p之间的距离值。FPFH只计算点p与其邻域内其他点的对应关系，如图3所示，只有一些重要的点对被计算了2次(图中黑色粗实线)，其余的点对只计算一次(图中黑色细实线)。

点云的特征点是指能够反映点云基本几何形状，对于描述点云的外观具有关键性作用的点，而这些特征点一般位于模型边缘或模型几何形状突变的区域，这些区域内点的法线朝向均比较散乱。如图4所示，在平缓部分(左侧框点)，邻域内的点的法线方向基本一致，故直方图集中在同一个子区间内；在特征明显部位(右侧框点)，邻域点的法线朝向散乱，直方图统计数据较为分散。

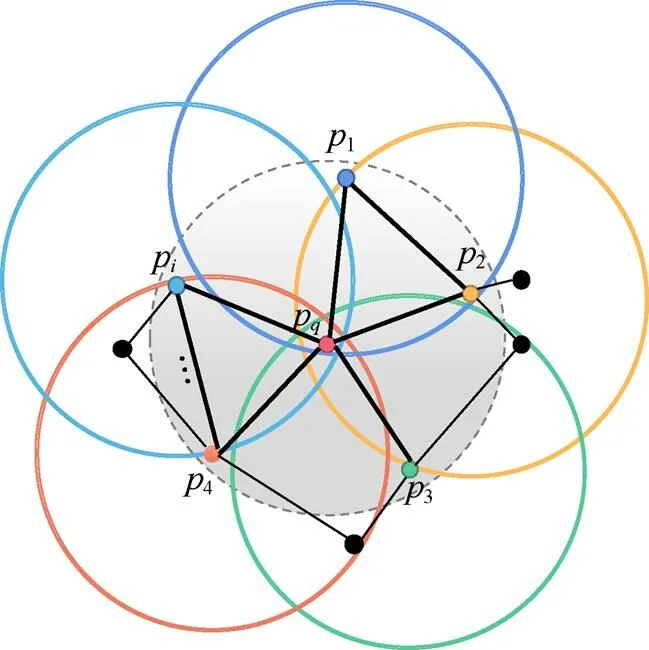
图3 FPFH计算区域示意图

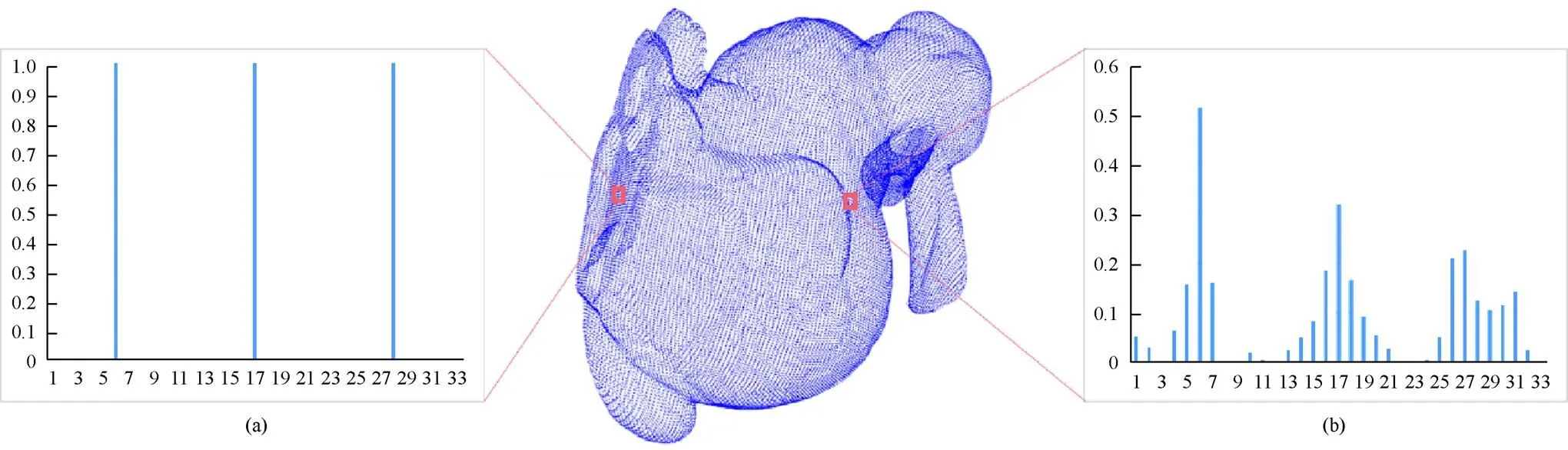
图4 FPFH计算结果示意图((a)非特征点FPFH计算结果结果；(b)特征点FPFH计算结果)

若直接用直方图来进行点云分类难以操作，每个点的直方图均包含3个特征元素的总计33个统计值(Point Cloud Library默认将每个特征元素划分为11个子区间进行统计)。故本文首先将该直方图逆向拆分为3个子直方图，再分别计算每个子直方图的标准差，以最大标准差来描述直方图分布情况，这样既能够较好地描述直方图的统计信息，又便于对点的特征强度进行评价，从而有效判别特征点和非特征点。

1.3 最远点采样算法(FPS)

FPS[7]是一种较为常见的采样算法，其计算流程如图5所示，具体步骤为：

步骤1.从原始数据中随机选取一个点0作为起始点，依次与剩余的–1个点计算距离并存入数组中，选取距离最远的点1加入到采样点集={-0,1}中。

步骤2.选取第个点时，计算采样点集中每一个点到所有点(非点)的距离，选取距离最小值作为非点到点集的距离存入数组中。

步骤3.从中选取距离值最大的点加入到采样点集中。

图5 FPS算法示意图

步骤4.=+1，重复步骤2和步骤3，直到采集到的点云数达到目标数量为止。

采样FPS算法后的点分布较为均匀，但每次选点都要计算一次与所有点的距离，时间复杂度接近于(2)，因此大多数学者采用FPS的改进算法来进行研究学习[23-26]。本文提出的改进算法，每次采样前先采个点，从中选出最远的点作为采样点，这样既能够选出位置相对较远的点，同时也提高了算法的计算效率。

1.4 标准化信息熵

信息熵[27]是一个重要的熵概念，含义非常丰富。其可用于描述点云的特征信息，某点的熵值越大，表明该点的信息量越大，整体的信息熵值越高，包含的信息越多，对物体的特征表达就越准确[28]。某点的信息熵为

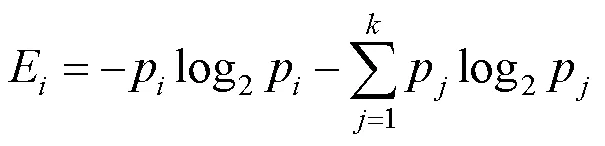
其中，E为点的熵值；p和p分别为和点的曲率概率分布，点是点的邻域内的点；C为点的平均曲率；为点邻域内点的个数。则整体的熵值为

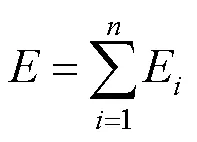
为了消除量纲的影响，本文对每个点的熵值进行了标准化处理。俞立平等[29]通过研究表明，现有的标准化方法，如极大值标准化、极差标准化、功效系数法等，均不具备评价功能，而sigmoid标准化方法具有评价功能，故对式(7)进行了标准化处理后可得

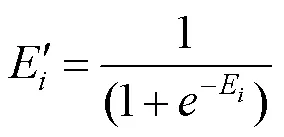
最后，计算得到信息熵值，即

其中，为整体熵值；为点云数。

2 算法流程

本文算法得到的采样点集由边界点、特征点和非特征点3部分组成，具体步骤如下：

输入：点集={(1,1,1), (2,2,2),···, (x,y,z)}；邻域；精简率；阈值；子区间数。

输出：精简后的点集。

步骤1.边界保留。输入点云数据，计算每个点的法线，根据法线和邻域寻找边界点，将边界点存入点集中。

步骤2.特征值计算。对于非边界点，根据式(6)计算其FPFH值。将得到的直方图按特征元素<,,>划分为3个子直方图，对每一个子直方图分别计算其标准差，取3个标准差中最大值作为该点的特征值。根据计算得到的特征值对点集进行升序排序。根据阈值将点集分为2部分，标准差小于阈值的点不需要精简，直接存入点集中，标准差大于阈值的点加入到点集中。

步骤3.改进的FPS算法采样。根据精简率、点云总数以及点集中的点云数计算得到需要采样的点云数，将点集划分为个子区间，根据需要采样的点云数和子区间数计算得到每个子区间需要采样的点云数。根据改进的FPS算法从每个子区间等间隔采个点，并将采样点加入到点集中。最后输出精简后的点集。

步骤1中，通过设置邻域搜索阈值可以调节查询的边界精度(即查询到的边界数)。并根据实际应用需要进行设置，经过实验分析，当查找到的边界点数占精简后点云总数的10%左右时，精简后的点云模型边缘较为完整，又能够在非边界区域采集更多的点。本文实验保留的边界点云数占精简后的5%～20%。

步骤2中，阈值的大小决定着最终精简后模型中非特征区域最终所能够保留的点云数量，当阈值很大时，精简后的模型特征点居多，在非特征区域容易出现较大的孔洞，而当阈值很小时，精简后的模型中点的分布较为均匀，整体保留较好，但特征点较少。需根据实际设置阈值大小，因为未对特征值进行归一化处理，所以阈值的取值较大，一般为[1, 20]。

步骤3中，子区间数的设置可影响算法的计算时间，在实验中根据模型点云规模不同将其大小一般设置为1 000～5 000。

边界查找部分的时间复杂度为()[17]。特征值部分主要是对直方图进行统计计算，其时间复杂度是()，为非边界点的点云数，为采样点邻域内的点数，计算标准差并找出最大标准差的时间复杂度为()。边界点的数量占总点云数的比值很小，趋近于点云总数，因此()≈()。对于采样部分，采样每个子区间需要计算次距离，为子区间内等间隔采样的点数，则采样完个子区间需要计算次距离，则采样部分的时间复杂度为()，子区间数乘以每个子区间内的点云数为非特征点的点云数，而非特征点的点云数也是趋近于点云总数的。故在最坏情况下，当每个子区间的采样点数的取值接近于时，采样部分的时间复杂度接近于()，即当精简率很低时，采样的时间复杂度约为()。故最坏情况下算法的时间复杂度为()，为等间隔采样的采样点数。

3 实验结果分析

以斯坦福大学三维扫描库中的点云数据作为测试数据，将本文算法与 FPS、非均匀网格法(Non-uniform)、基于k-means聚类的精简算法[8](K-means)以及基于自适应曲率熵的精简算法[12](Curvature entropy))进行对比分析，从可视化、信息熵和运行时间3个方面对算法进行评价。所有实验在Windows 10，64位操作系统中进行，基于Intel Core i5-10400F CPU，16 G内存，采用Visual Studio 2019编程实现。

3.1 视觉效果分析

为测试本文算法对不同规模和形状的点云模型的精简效果，在多个模型上测试了精简率(精简率=删减点云数/原始点云数×100%)为90%下的精简效果，实验结果如图6所示。

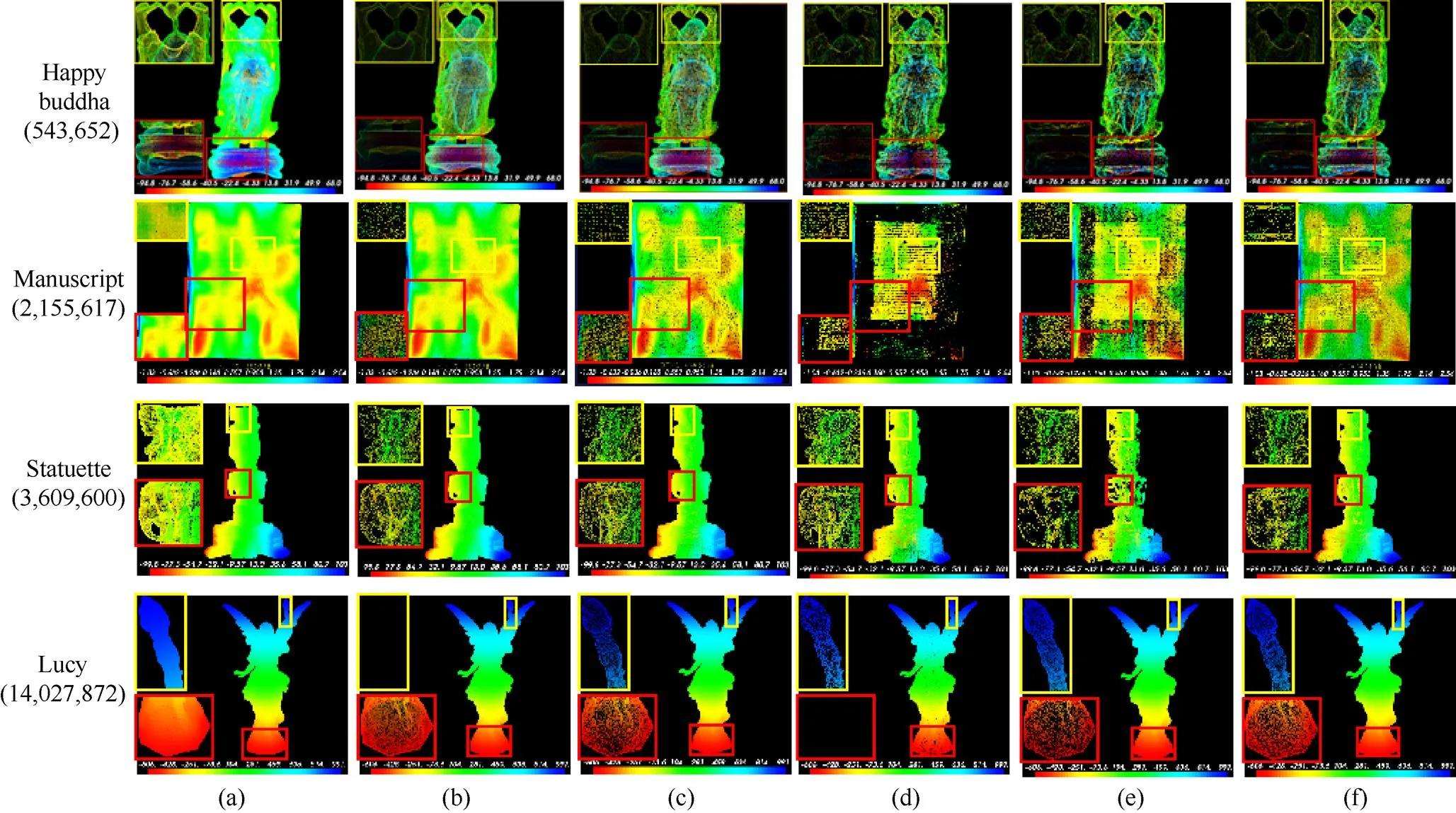
图6 不同模型精简结果((a)原始模型；(b)最远点采样法；(c)非均匀网格法；(d) k-means聚类法；(e)自适应曲率熵；(f)本文算法)

图6模型括号内数字为该模型的原始点云数，图中颜色代表点云的深度信息，黄色和红色框图为模型局部放大图。由图6可知，对于较小规模和特征信息较少的点云模型Happy buddha，5种算法的精简效果相近，均能保证模型整体的完整。相对而言，FPS算法和Non-uniform算法的整体性更好，而K-means算法、Curvature entropy算法和本文算法对特征信息的保留效果更好。

Manuscript为一张较为平整的牛皮纸，在中部写有文字，文字区域较纸面有一定的凹陷，特征信息主要为中部的文字书写痕迹。由图6可知，FPS算法和Non-uniform算法精简后的模型几乎无法看出中间的文字内容，K-means算法和Curvature entropy算法虽然对文字部分的保留效果较好，但在非文字区域容易出现大的孔洞，整体可视化效果较差。本文算法整体可视化效果最好，能够明显地识别出文字区域和非文字区域，模型表面也未出现明显孔洞。

对于结构复杂和数据量大的点云模型(Statuette和Lucy模型)，本文算法的精简效果也较好，可兼顾细节特征信息保留和保证精简模型的整体完整性。

图7为5种算法在不同精简率下对Dragon模型的精简可视化结果。由图可知，在精简率较小时，5种算法的精简效果均很相似，且能保证模型的整体完整；当精简率增大时，算法的精简差异就越来越大。Non-uniform算法的精简结果与FPS算法类似，但在细节特征上比FPS算法保留效果更好。K-means算法和Curvature entropy算法类似，均对细节特征保留较好，但当精简率增大时，精简模型表面容易出现较大的孔洞，Curvature entropy算法的整体性要稍好于K-means算法。本文算法的整体可视化效果最好，对模型的某些局部特征保留效果较佳(如Dragon模型的眼球部位)。

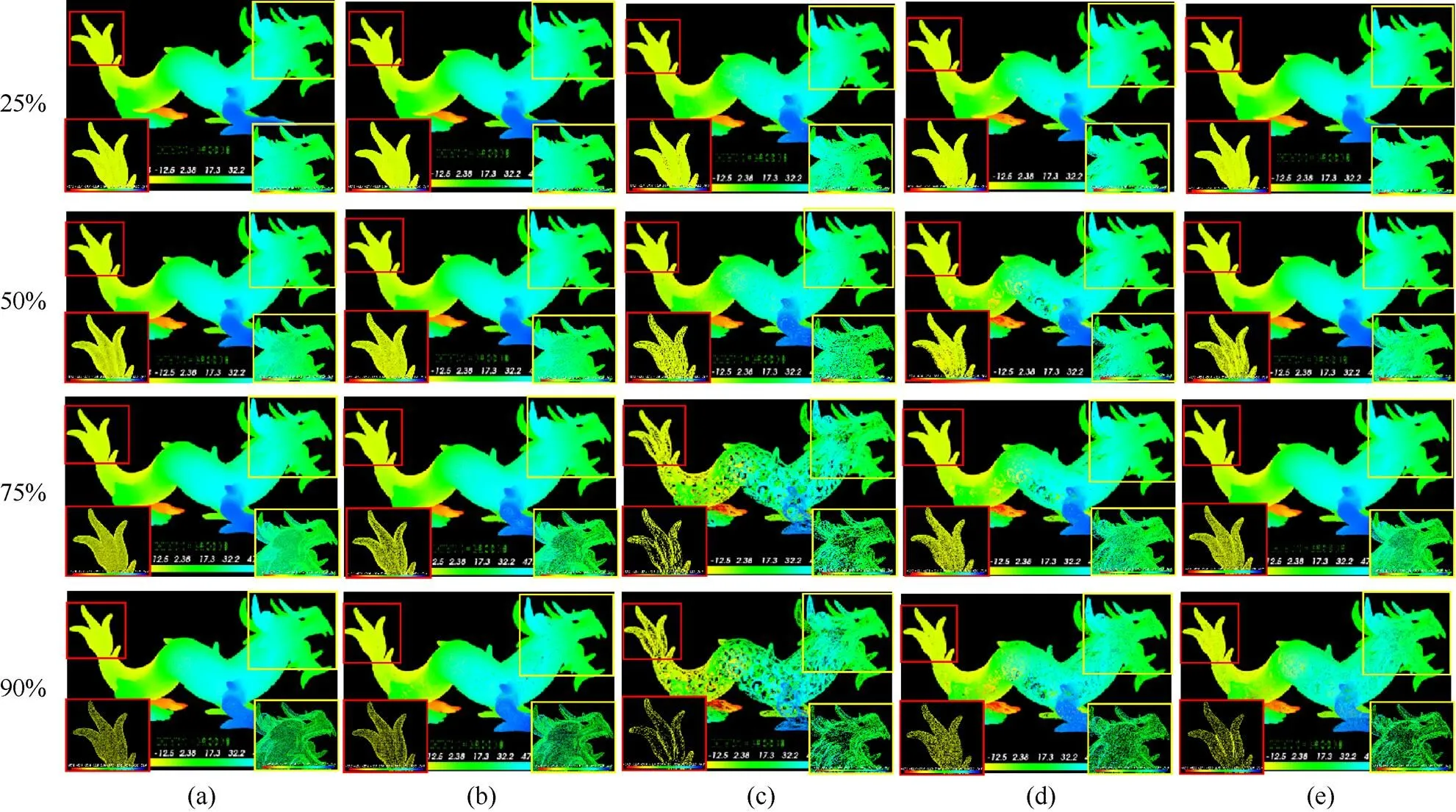
图7 不同精简率下Dragon模型精简结果((a)最远点采样法；(b)非均匀网格法；(c) k-means聚类法；(d)自适应曲率熵；(e)本文算法)

3.2 信息熵分析

信息熵评价方法能够对精简算法的精简质量进行定量评价。在相同的精简率下，不同算法精简后保留的点云数量略有差别，故本文在计算得到精简模型的标准化信息熵后，利用式(11)对熵值进行了均值化处理。表1列出了5种算法在精简率为90%下对各点云模型精简后的熵值计算结果。

由表1可知，在Happy buddha，Manuscript，Lucy和Dragon模型上，本文算法的熵值均是最高的，在Statuette模型上的熵值比Non-uniform算法的精简模型稍低一点，但差距很小。值得注意的是，采样点分布最均匀的FPS算法的熵值和特征信息保留最好的K-means算法和Curvature entropy算法精简得到的模型的熵值均不是最高的，在多数情况下，兼顾特征信息保留和整体完整性的算法的熵值更高。

为了验证本文所提出标准化信息熵的可行性，用本文算法对Dragon模型在90%精简率下进行精简，精简结果如图8所示，左侧模型整体性较差，但是细节特征保留较好，而右侧模型整体性最好，但特征信息保留较少。熵值计算结果见表2。

表1 5种算法的熵值计算结果

注：加粗数据为最优值

图8 90%精简率下Dragon模型精简结果

表2 Dragon模型的标准化信息熵熵值计算结果

注：加粗数据为最优值

由表2可知，无论是特征点较多的图8(a)模型还是特征点少的图8(d)模型，其标准化信息熵值均不是最高的，而相对而言，即保留了较多的特征点，又保证模型整体完整性的图8(c)模型的熵值最高，故本文算法能够较好地评价模型的精简效果。

3.3 运行时间分析

根据分析算法可知，FPS算法的时间复杂度为(2)，为点云数。Non-uniform算法经过不断优化，时间复杂度接近于()。K-means算法的主要计算是进行k-means聚类，故时间复杂度是()，其中为聚类数，为迭代次数。Curvature entropy算法主要时间花费在曲率熵的计算上，其时间复杂度为(log)。本文算法的时间复杂度为()，为子区间内等间隔采样的采样点数。表3为5种算法在90%精简率下对上述模型精简的运行时间。

表3 5种算法的运行时间(s)

注：加粗数据为最优值

由表3可知，Non-uniform算法的计算时间最短，本文算法的运行时间接近于Non-uniform算法。而与本文算法精简效果相近的K-means算法和Curvature entropy算法的运行时间花费比本文算法高得多，说明本文算法不仅能够保证精简质量，同时运行时间较短，可有效缩短点云预处理的时间。

4 结束语

随着三维扫描技术的不断发展，点云扫描速度越来越快，获取的点云数量也越来越大。如果不对得到的点云模型进行精简，后续的点云处理效率将会大大降低，为此本文提出了基于特征保持的点云精简算法。为了更好评价点云精简效果，还提出一种标准化的信息熵计算方法，通过对斯坦福大学三维扫描库中的点云数据实验表明，该算法的信息熵优于其他4种算法，能够在保证模型完整性的同时，尽可能地保留模型的特征信息，且算法运行效率高，具有较好的适用性。本文算法存在需要预先设置的参数过多，对于点数较少的点云简化效果不佳等问题。在未来的研究中，将减少算法的参数量，并设计一个自适应点云精简算法。

[1] PAULY M, GROSS M, KOBBELT L P. Efficient simplification of point-sampled surfaces[C]//IEEE Visualization, 2002. New York: IEEE Press, 2002: 163-170.

[2] MARTIN R R, STROUD I A, MARSHALL A D. Data reduction for reverse engineering[J]. The Mathematics of Surfaces, 1997, 10(1): 85-100.

[3] FILIP D, MAGEDSON R, MARKOT R. Surface algorithms using bounds on derivatives[J]. Computer Aided Geometric Design, 1986, 3(4): 295-311.

[4] SUN W, BRADLEY C, ZHANG Y F, et al. Cloud data modelling employing a unified, non-redundant triangular mesh[J]. Computer-Aided Design, 2001, 33(2): 183-193.

[5] LEE K H, WOO H, SUK T. Point data reduction using 3D grids[J]. The International Journal of Advanced Manufacturing Technology, 2001, 18(3): 201-210.

[6] MIAO Y W, PAJAROLA R, FENG J Q. Curvature-aware adaptive re-sampling for point-sampled geometry[J]. Computer-Aided Design, 2009, 41(6): 395-403.

[7] ELDAR Y, LINDENBAUM M, PORAT M, et al. The farthest point strategy for progressive image sampling[J]. IEEE Transactions on Image Processing, 1997, 6(9): 1305-1315.

[8] 贺一波, 陈冉丽, 吴侃, 等. 基于k-means聚类的点云精简方法[J]. 激光与光电子学进展, 2019, 56(9): 96-99.

HE Y B, CHEN R L, WU K, et al. Point cloud simplification method based on k-means clustering[J]. Laser & Optoelectronics Progress, 2019, 56(9): 96-99 (in Chinese).

[9] YANG Y, LI M, MA X. A point cloud simplification method based on modified fuzzy C-means clustering algorithm with feature information reserved[EB/OL]. [2021-12-25]. https:// downloads.hindawi.com/journals/mpe/2020/5713137.pdf.

[10] MAHDAOUI A, SBAI E H. 3D point cloud simplification based on-nearest neighbor and clustering[EB/OL]. [2021- 12-25]. https://downloads.hindawi.com/journals/am/2020/882 5205.pdf.

[11] JI C Y, LI Y, FAN J H, et al. A novel simplification method for 3D geometric point cloud based on the importance of point[J]. IEEE Access, 2019, 7: 129029-129042.

[12] WANG G L, WU L S, HU Y, et al. Point cloud simplification algorithm based on the feature of adaptive curvature entropy[J]. Measurement Science and Technology, 2021, 32(6): 065004: 1-065004: 12.

[13] ZHANG K, QIAO S Q, WANG X H, et al. Feature-preserved point cloud simplification based on natural quadric shape models[J]. Applied Sciences, 2019, 9(10): 2130.

[14] XUAN W, HUA X H, CHEN X J, et al. A new progressive simplification method for point cloud using local entropy of normal angle[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(4): 581-589.

[15] SHOAIB M, CHEONG J, KIM Y, et al. Fractal bubble algorithm for simplification of 3D point cloud data[J]. Journal of Intelligent & Fuzzy Systems, 2019, 37(6): 7815-7830.

[16] QI J K, HU W, GUO Z M. Feature preserving and uniformity-controllable point cloud simplification on graph[C]//2019 IEEE International Conference on Multimedia and Expo. New York: IEEE Press, 2019: 284-289.

[17] SILPA-ANAN C, HARTLEY R. Optimised KD-trees for fast image descriptor matching[C]//2008 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2008: 1-8.

[18] 孙殿柱, 范志先, 李延瑞. 散乱数据点云边界特征自动提取算法[J]. 华中科技大学学报: 自然科学版, 2008, 36(8): 82-84.

SUN D Z, FAN Z X, LI Y R. Automatic extraction of boundary characteristic from scatter data[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 2008, 36(8): 82-84 (in Chinese).

[19] RUSU R B, MARTON Z C, BLODOW N, et al. Learning informative point classes for the acquisition of object model maps[C]//2008 10th International Conference on Control, Automation, Robotics and Vision. New York: IEEE Press, 2008: 643-650.

[20] RUSU R B, BLODOW N, MARTON Z C, et al. Aligning point cloud views using persistent feature histograms[C]//2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. New York: IEEE Press, 2008: 3384-3391.

[21] WAHL E, HILLENBRAND U, HIRZINGER G. Surflet-pair- relation histograms: a statistical 3D-shape representation for rapid classification[C]//The 4th International Conference on 3-D Digital Imaging and Modeling. New York: IEEE Press, 2003: 474-481.

[22] RUSU R B, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration[C]//2009 IEEE International Conference on Robotics and Automation. New York: IEEE Press, 2009: 3212-3217.

[23] MOENNING C, DODGSON N. Fast marching farthest point sampling[EB/OL]. [2021-12-15]. http://citeseerx.ist.psu.edu/ viewdoc/download;jsessionid=1A9C100269551371F03B7D91B0B7BDBE?doi=10.1.1.14.1047&rep=rep1&type=pdf.

[24] SCHLÖMER T, HECK D, DEUSSEN O. Farthest-point optimized point sets with maximized minimum distance[C]// The ACM SIGGRAPH Symposium on High Performance Graphics – HPG’11. New York: ACM Press, 2011: 135-142.

[25] 陈境焕. 基于深层神经网络的三维点云细粒度分割算法研究[D]. 广州: 广东工业大学, 2020.

CHEN J H. Research on fine-grained segmentation algorithm of 3D point cloud based on deep neural network[D]. Guangzhou: Guangdong University of Technology, 2020 (in Chinese).

[26] 马益飞. 基于特征线的兵马俑点云简化方法研究[D]. 西安: 西北大学, 2021.

MA Y F. Research on simplification method for point cloud of terracotta warriors based on characteristic line[D]. Xi’an: Northwest University, 2021 (in Chinese).

[27] SHANNON C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3-55.

[28] 朱广堂, 叶珉吕. 基于曲率特征的点云去噪及定量评价方法研究[J]. 测绘通报, 2019(6): 105-108.

ZHU G T, YE M L. Research on the method of point cloud denoising based on curvature characteristics and quantitative evaluation[J]. Bulletin of Surveying and Mapping, 2019(6): 105-108 (in Chinese).

[29] 俞立平, 宋夏云, 王作功. 评价型指标标准化与评价方法对学术评价影响研究: 以TOPSIS评价方法为例[J]. 情报理论与实践, 2020, 43(2): 15-20, 54.

YU L P, SONG X Y, WANG Z G. Study on the influence of evaluation standardization and evaluation methods on academic evaluation: taking TOPSIS evaluation method as an example[J]. Information Studies: Theory & Application, 2020, 43(2): 15-20, 54 (in Chinese).

A scattered point cloud simplification algorithm based on FPFH feature extraction

LI Hai-peng, XU Dan, FU Yu-ting, LIU Yan-an, ZHANG Ting-ting

(School of Information Science and Engineering, Yunnan University, Kunming Yunnan 650500, China)

To address the large amount of redundant data in the original point cloud, a point cloud simplification algorithm based on fast point feature histograms (FPFH) feature extraction was proposed, effectively taking into account the retention of feature information and overall integrity. Firstly, the algorithm sought and retained the boundary points of the original model. Then, the FPFH value of non-boundary points were calculated, thus producing the feature value of the point cloud. After sorting the feature values, the non-boundary points were divided into the feature region and the non-feature region, retaining the points in the feature region. Finally, the non-feature region was divided intosub-intervals, and the improved farthest point sampling algorithm was employed to sample each sub-interval. The proposed algorithm was compared with the farthest point sampling algorithm, non-uniform grid method, k-means algorithm, and adaptive curvature entropy algorithm, and the simplified point cloud was evaluated by the standardized information entropy evaluation method. Experimental results show that the proposed algorithm outperforms other simplification algorithms. In addition, the visualization results indicate that the proposed algorithm can not only ensure the integrity of the simplified model but also retain most of the feature information of the point cloud.

point cloud simplification; fast point feature histograms; farthest point sampling; boundary reservation; standardized information entropy

25 November，2021；

National Natural Science Foundation of China (61761046, 62061049, 62162068); Yunnan Province “Ten Thousand Talents Program” Yunling Scholars Special Project (YNWR-YLXZ-2018-022); Yunnan Provincial Science and Technology Department-Yunnan University “Double First Class” Construction Joint Fund Project (2019FY003012); Graduate Research and Innovation Foundation of Yunnan University (Y2000211)

LI Hai-peng (1997-), master student. His main research interests cover image processing and computer vision. E-mail：lihaipeng@mail.ynu.edu.cn

TP 391

10.11996/JG.j.2095-302X.2022040599

A

2095-302X(2022)04-0599-09

2021-11-25；

2022-02-25

25 February，2022

国家自然科学基金项目(61761046，62061049，62162068)；云南省“万人计划”云岭学者专项(YNWR-YLXZ-2018-022)；云南省科技厅-云南大学“双一流”建设联合基金项目(2019FY003012)；云南大学研究生科研创新项目(Y2000211)

李海鹏(1997-)，男，硕士研究生。主要研究方向为图像处理和计算机视觉。E-mail：lihaipeng@mail.ynu.edu.cn

徐 丹(1968-)，女，教授，博士。主要研究方向为计算机图形图像、视觉及人工智能、文化计算等。E-mail：danxu@ynu.edu.cn

XU Dan (1968-), professor, Ph.D. Her main research interests cover computer graphics, computer vision, artificial intelligence, cultural computing, etc. E-mail：danxu@ynu.edu.cn