轨道车辆车钩垂向最大摆角计算方法

杨 晨， 池茂儒， 吴兴文， 蔡吴斌， 刘开成

(1.西南交通大学 牵引动力国家重点实验室，成都 610031；2.西南交通大学 机械工程学院，成都 610031)

连挂车辆在通过曲线的过程中，受线路、悬挂故障、牵引制动等因素的影响，车端部件会产生较大的相对运动，因此在新型车辆设计时，为保证列车能够安全通过曲线，需要对连挂车辆的车钩最大摆角进行计算和校核。其中，车钩垂向最大摆角的校核是列车安全通过竖曲线的重要保障，准确计算车辆在运营过程中车钩垂向最大摆角具有重要意义。

针对车钩摆角的计算方法，已有了较多研究，现有的方法主要是几何法和动力学法。几何法方面，罗仁等[1]首先基于CJJ 96—2003《地铁限界标准》计算了车体动态偏移量，考虑车辆纵向位置等因素，采用几何法计算了车钩摆角，分析了连挂车辆水平几何曲线通过能力；张兰等[2]提出了基于空间坐标位姿变换理论的连挂车辆通过曲线段时车钩转角的计算方法，并将计算结果与文献计算结果进行了比较，验证了该方法的正确性；在动力学法方面，丁奥等[3]采用SIMPACK软件建立了连挂车辆多刚体动力学模型，计算了通过水平几何曲线时的车钩摆角，并将动力学仿真结果与理论计算法进行了对比分析。此外，动力学仿真也已经广泛用于铁道车辆曲线通过计算[4-6]。

由于连挂车辆在实际运行中，不免会出现悬挂故障，如一系钢弹簧断裂、二系空气弹簧失气等，这些故障均会对车钩垂向摆角产生明显影响，故在计算车钩垂向最大摆角时必须考虑悬挂故障工况。传统的悬挂故障下车钩垂向最大摆角(以下简称为车钩最大摆角)的计算方法，大多认为故障时悬挂元件直接变形到位[7]，在此基础上，采用纯理论计算的方式求得车钩最大摆角。

在悬挂故障力学建模方面，刘国云等[8]依据黏滑接触模型，建立了钢簧失效工况下的车辆系统动力学模型，分析了钢簧失效对车辆动力学性能的影响；高浩等[9]建立了具有刚度衰变特性的空气弹簧失气模型和非线性黏滑接触模型,结合车辆系统动力学,研究了空气弹簧失气车辆的安全性。戚壮等[10]基于气动力学理论与函数拟合方法，建立了空气弹簧系统的三维耦合动力学模型，并将该模型与高速动车组整车动力学模型进行了联合仿真，研究了空气弹簧故障模式下转向架的动力学响应。

本文首先分析了传统常规计算法的不足，并针对这些不足，考虑单一钢弹簧断裂和单一空气弹簧失气两种故障，进一步提出了基于含悬挂故障的车辆动力学模型的车钩最大摆角计算方法。基于该方法，分析了某型地铁连挂车辆悬挂故障条件下的车钩最大摆角，并与常规计算法进行了对比，研究了悬挂故障下关键参数对车钩最大摆角的影响规律。

1 悬挂故障下车钩最大摆角计算方法

1.1 常规计算法介绍

常规计算法在计算车钩最大摆角时，考虑连挂车辆同向点头且车钩处于压缩状态，此时车钩摆臂角最恶劣。图1为连挂车辆通过竖曲线同向顺时针点头的几何位置示意图，假设C端发生悬挂故障。在图1中:A为前车前车钩摆臂点;C为前车后车钩摆臂点;D为后车前车钩摆臂点;E为后车后车钩摆臂点;R为竖曲线半径;hcg为车钩距离轨顶面的高度;Y1为C点的垂向向下偏移量;Y2为A点垂向向上偏移量;Y3为D点的垂向向上偏移量;Y4为E点垂向向下偏移量;Lcg为车钩压缩状态的长度;θcg为车钩垂向摆角。其中，车钩摆臂点指车钩与车体的车钩安装座之间的相对回转中心。

常规计算法依据CJJ 96—2018《地铁限界标准》直接计算各车钩摆臂点处的垂向偏移量Y1,Y2,Y3,Y4，其中计算Y1时考虑悬挂故障对C点垂向偏移量的影响，在此基础上通过几何法求得车钩最大摆角θcg。CJJ 96—2018《地铁限界标准》中，由悬挂故障引起的故障端车钩摆臂点垂向向下偏移量ΔYd计算过程如下

(1)

式中:ΔYpsgz为钢弹簧断裂引起的车钩摆臂点处的垂向向下偏移量;Δhps为钢弹簧断裂时的下降量;n为车钩摆臂点到相邻中心销的距离;a为车辆定距；ΔYssgz为空簧失气引起的车钩摆臂点处的垂向向下偏移量;Δhss为空簧失气时的下降量。

图1 常规计算法的几何示意图

可以看出，常规论计算法没考虑车体的柔性变形；在考虑悬挂故障时，一般认为故障悬挂直接变形到位，由式(1)直接计算悬挂故障引起的车钩摆臂点处的偏移量，不仅不考虑该转向架其他悬挂由于故障引起的冲击变形，也不考虑应急橡胶弹簧的冲击变形等；且未考虑由悬挂故障引起的非故障端车钩摆臂点处A的偏移量。针对常规计算法的以上不足，本文提出了基于含故障的车辆动力学模型的最大摆角计算方法。

1.2 基于含故障的车辆动力学模型的摆角计算方法

1.2.1 摆角计算方法

图2给出了基于含故障的车辆动力学模型的摆角计算方法的几何示意图。在图2中:B为前车后中心销点;C′为前车车体变形后的后车钩摆臂点;C为不考虑车体变形的前车后车钩摆臂点;L11为车钩摆臂点到中心销的距离;ΔhCT为车体的柔性垂直变形。其余参数含义参考1.1节。

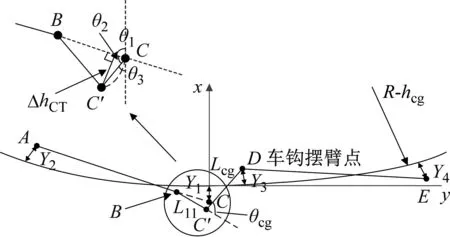
图2 新方法的几何示意图

车钩摆臂点的偏移量Y1,Y2,Y3,Y4，均采用CJJ 96—2018《地铁限界标准》中[11]的公式计算。其中，悬挂故障下车钩摆臂点的垂向向下偏移量Y1为

(2)

ΔYd=hgz-hzc

(3)

式中:ΔYd为悬挂故障引起的故障端车钩摆臂点垂向向下偏移;hgz为采用含故障的多刚体动力学模型仿真得到的故障发生瞬间C端车钩摆臂点的最低高度;hzc为采用正常多刚体动力学模型仿真得到的同时刻C端车钩摆臂点的高度。其余变量含义参考文献[11]。采用动力学仿真计算ΔYd，可以考虑故障时各悬挂的实际冲击变形。

非故障端车钩摆臂点的垂向向上偏移量Y2为

(4)

(5)

进一步，考虑车体的柔性变形后，故障端车钩摆臂点C′坐标的计算过程为

θ3=π-θ1-θ2

yC′=yC-2cosθ3cosθ2L11

xC′=xC-2sinθ3cosθ2L11

(6)

式中，车体的柔性变形ΔhCT需依据刚柔耦合动力学模型计算。最后，采用二分法确定连挂车辆的具体姿态、位置与车钩长度，得到车钩最大摆角θcg。

1.2.2 含悬挂故障的连挂车辆动力学建模

故障引起的悬挂冲击变形会影响车钩摆臂点处的偏移量Y1,Y2，进一步影响车钩最大摆角，由式(3)、式(5)可以看出，计算车钩摆臂点处的偏移量需要借助车辆动力学模型；此外，现实中的车体并不是严格的刚体，具有一定的柔性[12-13]，当悬挂故障发生时，车体柔性变形ΔhCT对车钩摆角也有一定的影响。因此，本文针对某型地铁连挂车辆分别建立了包含钢簧断裂和空气弹簧失气的多刚体动力学模型和刚柔耦合动力学模型，如图3所示。车辆基本参数见表1，其中一系悬挂采用螺旋双卷钢弹簧，二系悬挂采用自由膜式空气弹簧。为了保证计算精度，截取车体的前45阶模态制作柔性车体，前5阶模态分析结果如表2所示。

(a) 含故障的多刚体动力学模型

表1 车辆基本参数

表2 车体前5阶模态分析结果

刚柔耦合动力学模型中对车体进行弹性化处理，其他部件视为刚体，建立柔性车体模型的步骤如下：首先采用Hypermesh对车体的三维实体模型进行几何清理，并划分网格；然后采用ANSYS对有限元结构进行模态分析和子结构缩减[14]，得到截断模态的质量矩阵和刚度矩阵，导入到SIMPACK软件中，建立连挂车辆的刚柔耦合动力学模型。

一系钢弹簧故障过程模型见图4。车辆一系悬挂包括钢弹簧内外圈、橡胶垫和一系上、下止挡销等。正常工况下，构架与轴箱之间通过钢簧与橡胶垫串联提供支撑刚度，当断簧发生时，构架止挡下降h0的高度后，构架止挡与轴箱止挡相接触，并向下冲击，此时轴箱通过一系橡胶堆支撑着构架，由于本文重点关注垂向偏移，故构架止挡与轴箱止挡之间横向考虑为非线性摩擦接触。在图4中:K1为钢簧垂向刚度;K2为橡胶堆的垂向刚度;K3为钢簧横向刚度;K4为橡胶堆横向刚度；C1为钢簧垂向阻尼;C2为橡胶堆的垂向阻尼;C3为钢簧横向阻尼;C4为橡胶堆横向阻尼；μ1为构架止挡与轴箱止挡之间的摩擦因数;h0为一系止挡间隙。

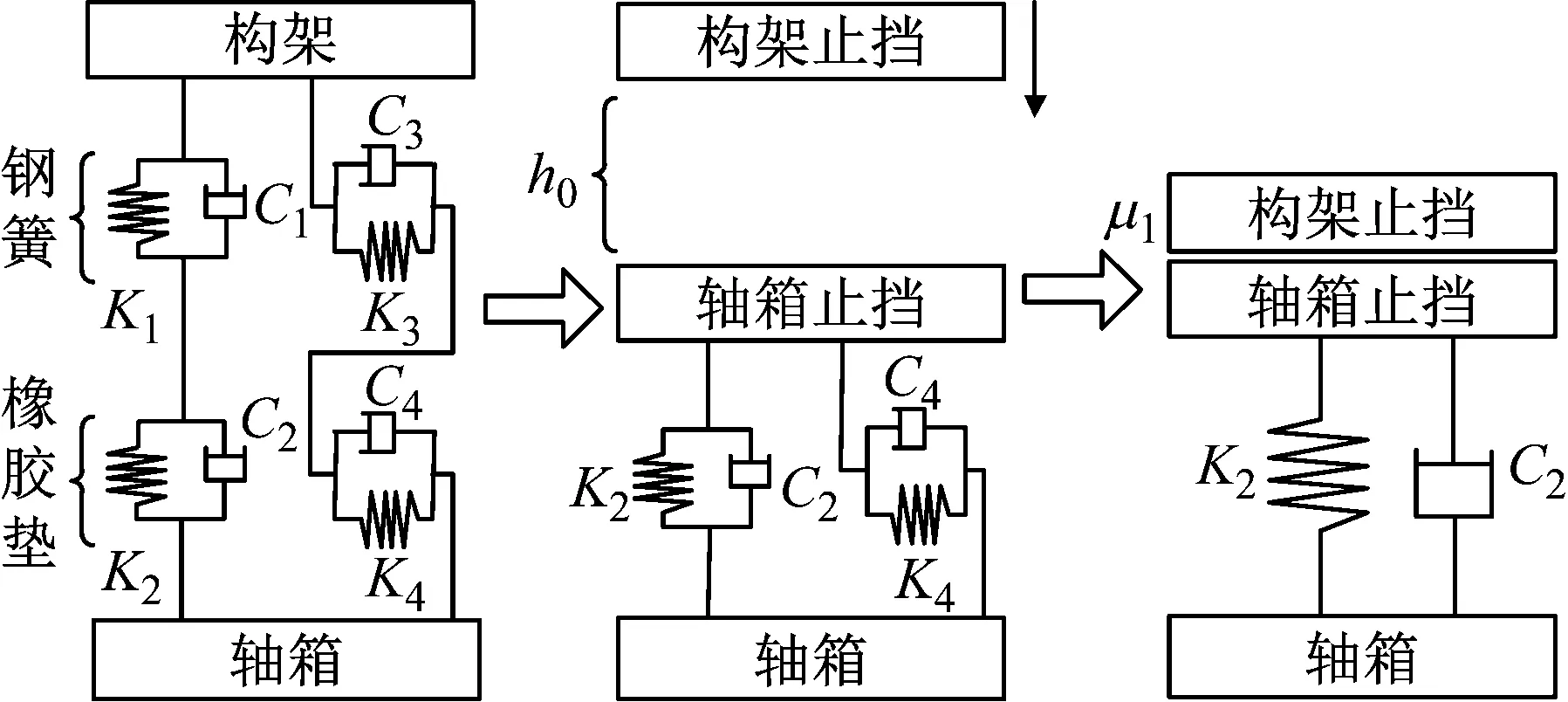
图4 一系钢簧断裂过程模型

止挡接触时的冲击过程等效模型见图5。从图5可以看出，钢簧未发生断裂障时，一系悬挂垂向刚度为橡胶堆与钢簧的串联刚度，故障发生后，在上止挡与下止挡接触前，一系悬挂垂向刚度为0，接触后的一系悬挂垂向刚度仅为橡胶堆刚度K2。

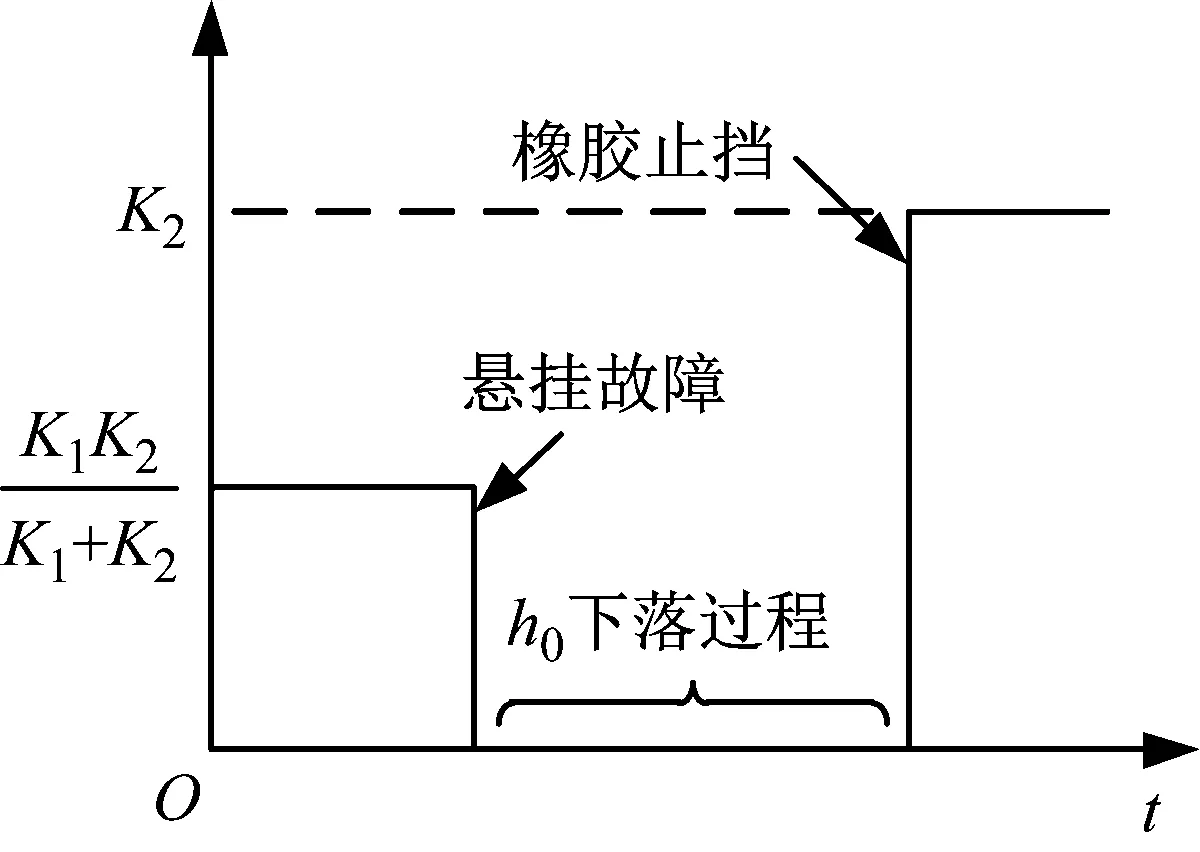
图5 冲击过程等效模型

构架止挡与轴箱止挡之间的法向力为

(7)

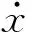
非线性摩擦接触力的计算方法为

(8)

式中:vT为相对滑动速度;vlim为产生滑动摩擦的临界速度。

二系失气故障过程模型见图6。车辆系统使用的空气弹簧本体一般由上盖板、橡胶气囊、下座和应急弹簧组成，车体上的上空气弹簧座与空气弹簧上盖板相连，构架上的下空气弹簧座与应急弹簧相连。将空气弹簧从失气发生到上盖板磨耗板与应急弹簧磨耗板接触的过程定义为失气过程，该过程的时间极短，故本文将该过程的刚度变化简化为瞬态过程。

当左侧空气弹簧失气发生时，因右侧空气弹簧与其连通，所以右侧空气弹簧同样失气，且右侧空气弹簧比左侧空气弹簧失气时间延迟tsz。失气时，两侧车体空簧座下降h1的高度后，上盖板磨耗板与应急弹簧磨耗板接触，并产生向下冲击，二者之间考虑为非线性摩擦接触，此时空簧不再提供垂向支撑，垂向刚度仅由应急弹簧提供。图6中:K5为空簧垂向刚度;K6为应急弹簧的垂向刚度;K7为空簧横向刚度;K8为应急弹簧横向刚度；C5为空簧垂向阻尼;C6为应急弹簧的垂向阻尼;C7为空簧横向阻尼;C8为应急弹簧横向阻尼;μ2为上盖板磨耗板与应急弹簧磨耗板之间的摩擦因数;h1为空气弹簧气囊间隙。失气时，上下盖板接触时的冲击过程等效模型参考图6，失气端车体与构架之间的法向力和非线性摩擦接触力参考式(7)和式(8)计算。

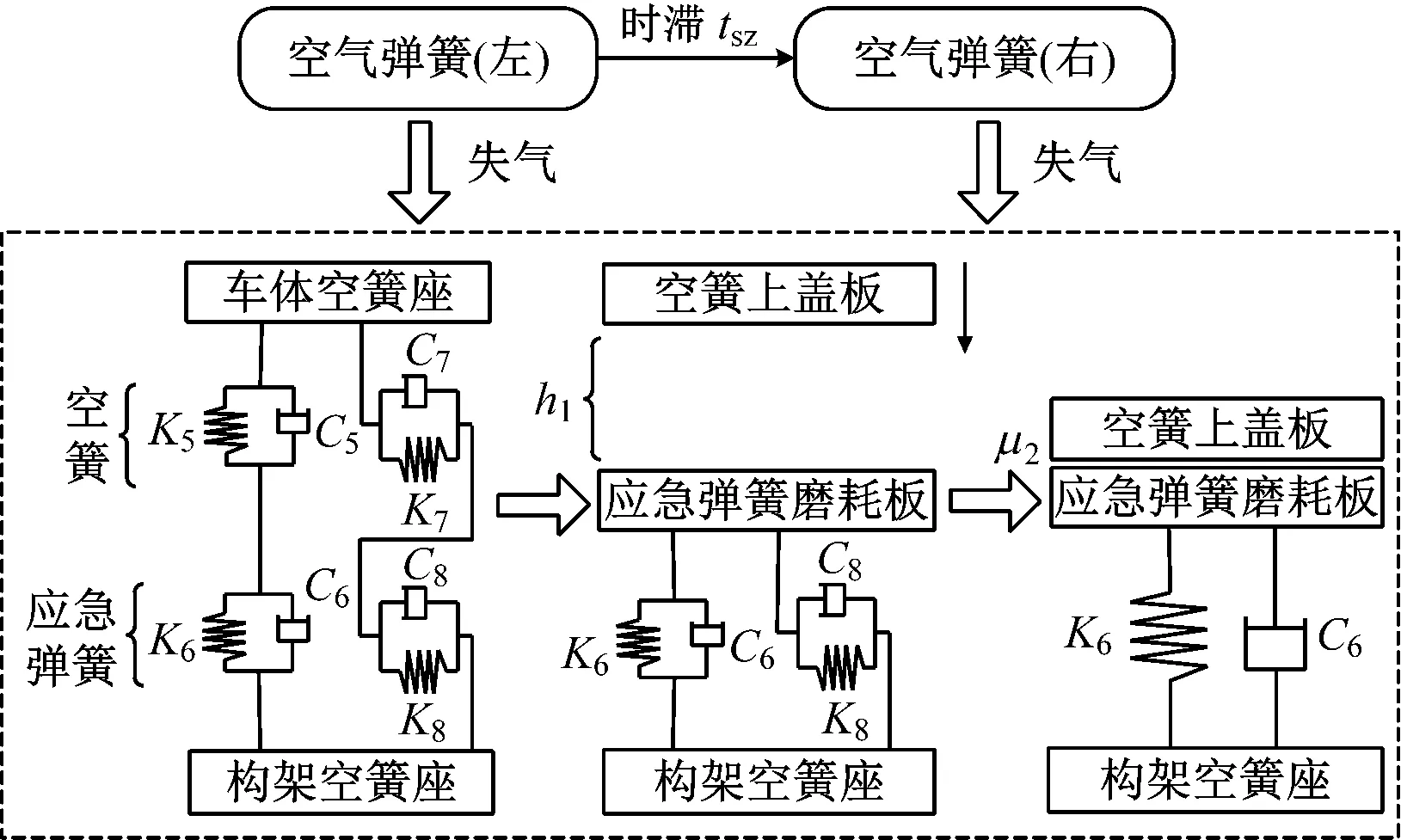
图6 二系空簧失气过程模型

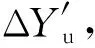
2 悬挂故障下车钩最大摆角分析

本章将针对某型地铁连挂车辆，对其车钩最大摆角开展分析。计算工况依据该型地铁车辆的实际工程需求设定为：线路为半径2 000 m的竖曲线，一系橡胶止挡间隙h0取值为30 mm，二系空气弹簧气囊间隙h1取值为20 mm。

此外，动力学仿真时轨道谱设置为美国五级谱，列车速度为40 km/h，二系空簧时滞失气时间为0.2 s。在仿真过程中，一系、二系故障均设置为4 s触发。其中，一系悬挂故障工况，假设只有2车一位轮对左轮处的钢弹簧发生完全断裂，其他位置的钢弹簧都正常；二系悬挂故障，假设只有2车前转向架左侧的空气弹簧发生失气故障，其他位置的空气弹簧都正常。

2.1 故障引起的车体柔性变形

基于刚柔耦合动力学模型，分别得到钢弹簧断裂和空气弹簧失气的车体垂向弯曲变形量ΔhCT，见图7、图8。

由图7可以看出，钢弹簧断裂对车体垂向弯曲变形的影响不明显，最大变形量为0.19 mm，这是由于钢簧断裂，构架下移，车体在下移过程中，空气弹簧起到了缓冲作用，加之车体刚度较大，故车体未产生明显变形。

图7 钢簧断裂下2车车体垂向弯曲变形

由图8可以看出，二系失气对车体垂向弯曲变形的影响较大，最大变形量为1.55 mm，这是由于应急弹簧刚度大，二系失气时，车体在下移过程中，重力势能大部分转换为了车体的应变能，故相比一系故障工况，车体产生了较为明显的变形。

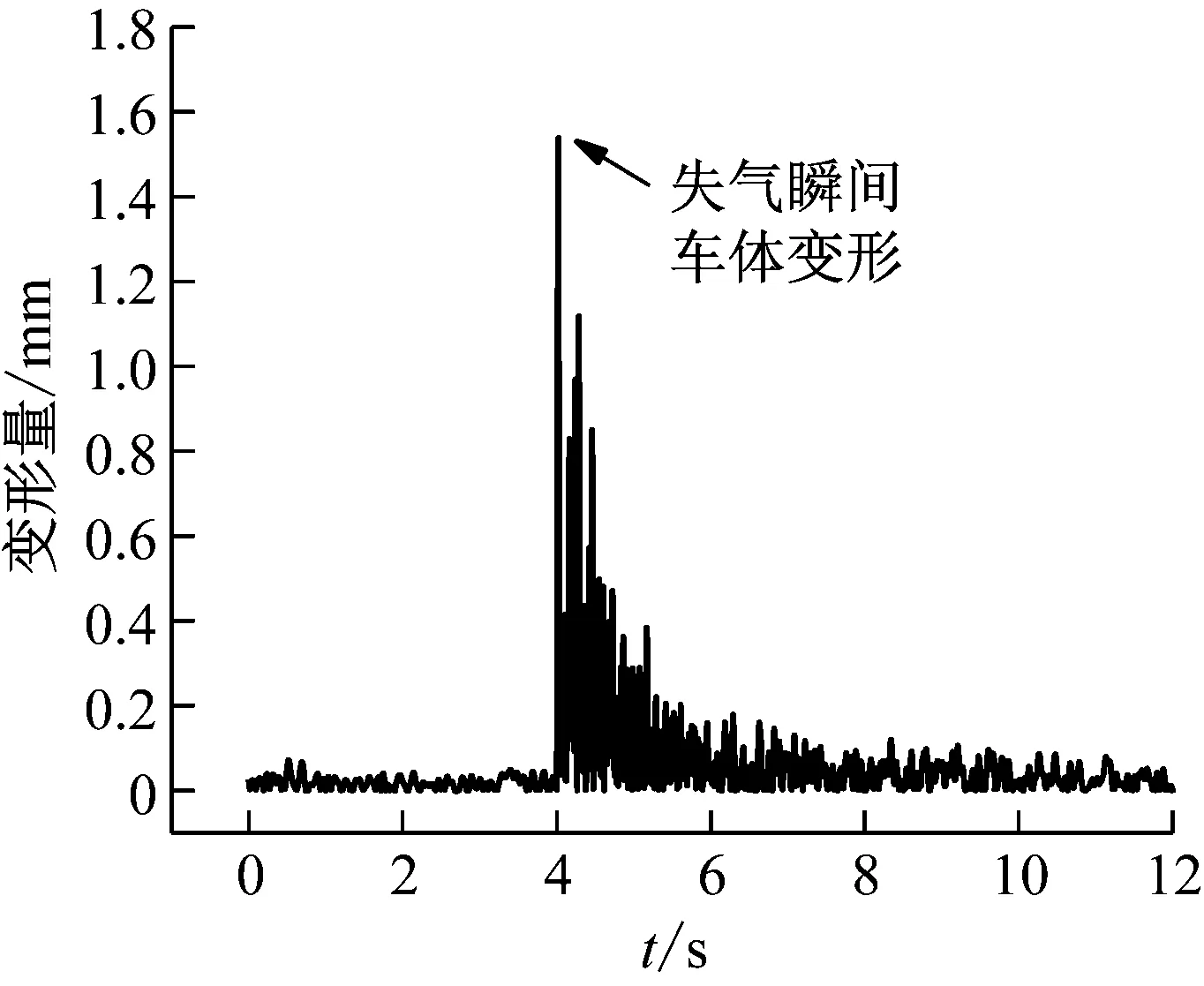
图8 空簧失气下2车车体垂向弯曲变形

2.2 故障引起的车钩摆臂点垂向偏移

本文提出的新方法基于动力学仿真，在考虑悬挂故障下降量的基础上，进一步考虑了其他悬挂的冲击变形以及应急弹簧的变形等，这些变形将对车钩摆臂点的偏移产生影响。同时新方法也考虑了由悬挂故障引起的非故障端车钩摆臂点处的偏移量，使计算过程更接近实际。

一系故障时，2车一位转向架一系钢簧的垂向位移变化见图9；二系故障时，2车空气弹簧的垂向位移变化见图10。

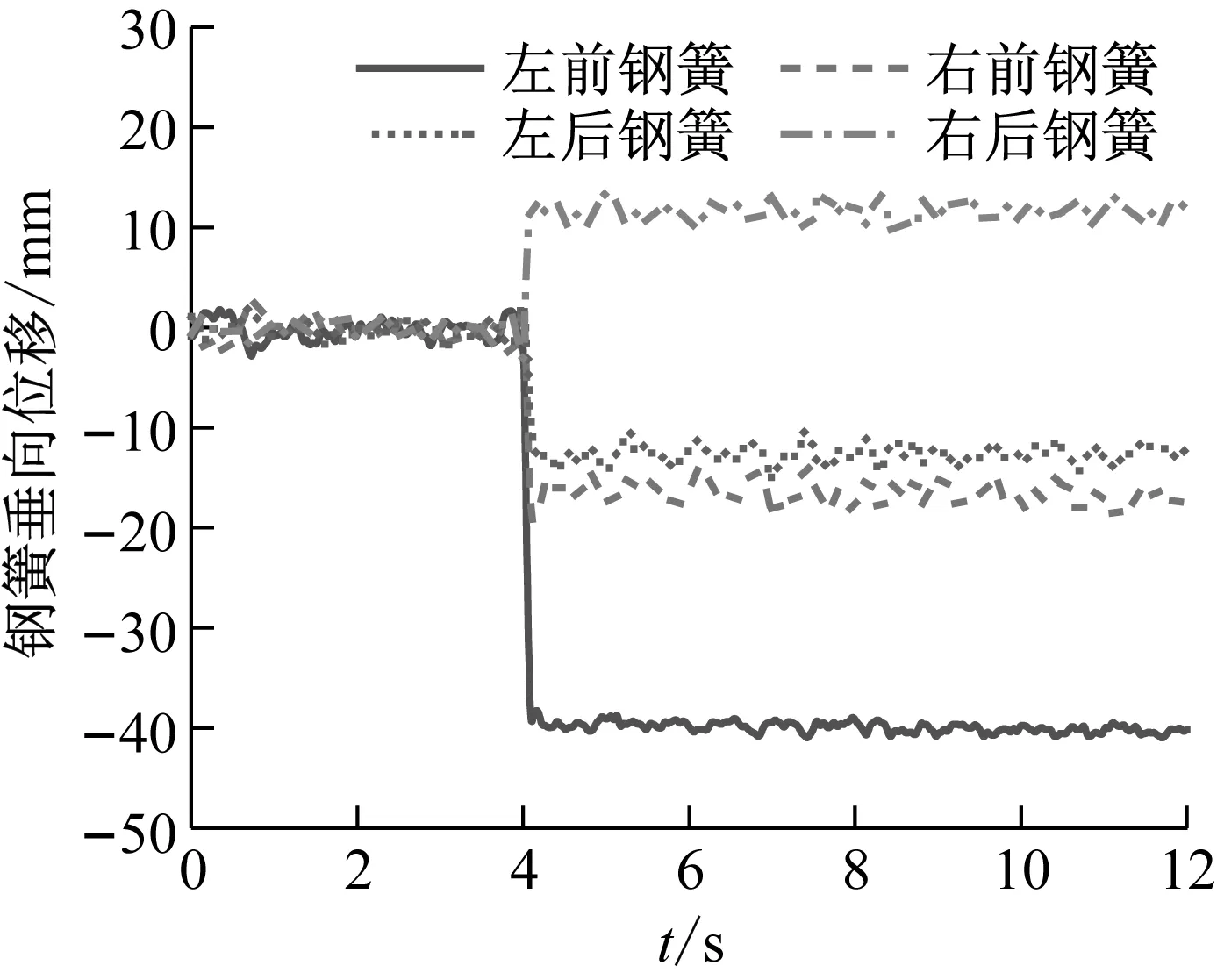
图9 2车一位转向架一系钢簧垂向位移

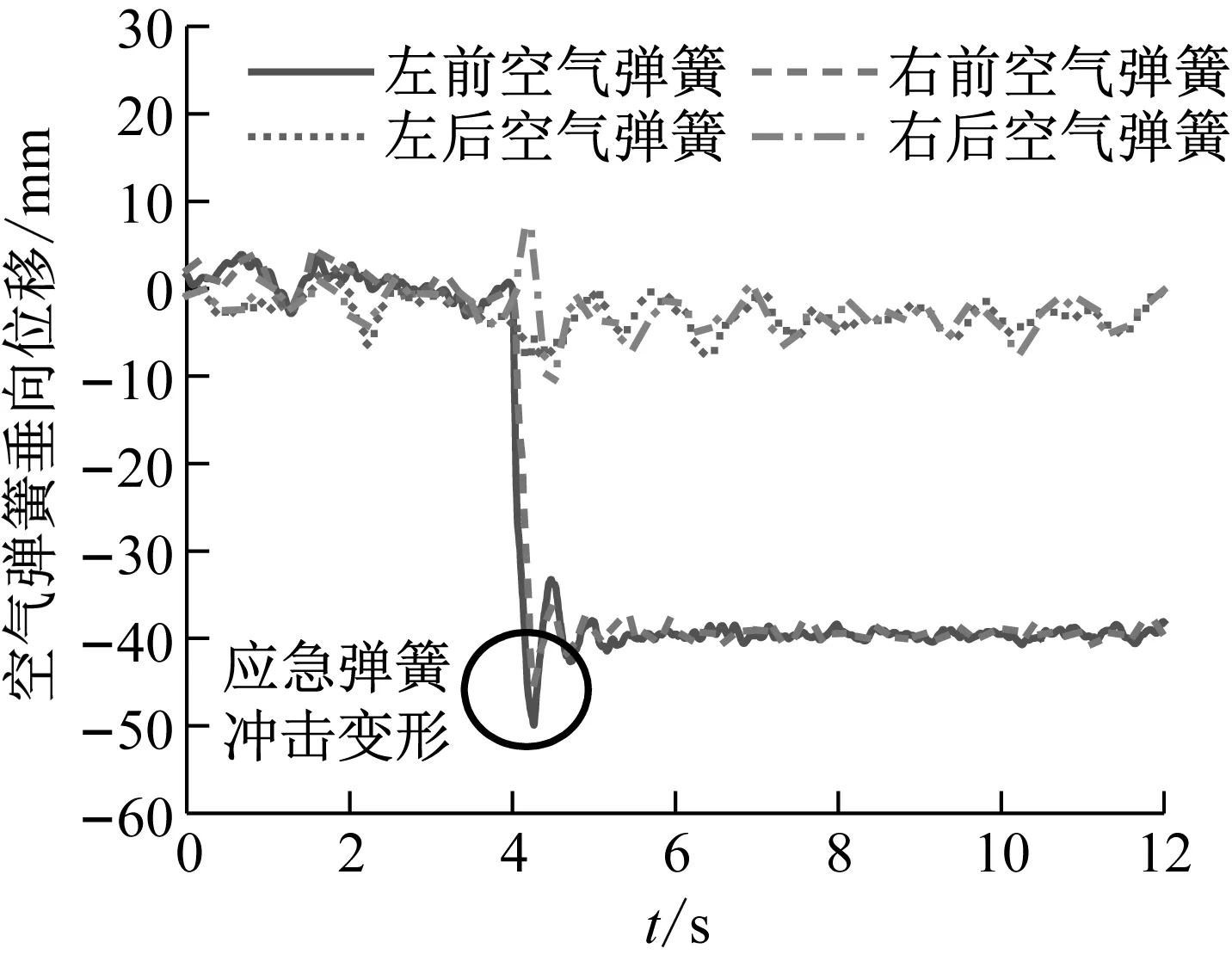
图10 2车空气弹簧垂向位移

由图9可以看出：当一位轮对左侧的钢弹簧发生断裂后，一位、二位轮对各钢弹簧的位移均会发生冲击变形，钢簧载荷将重新分配。其中，断裂钢簧下降了40 mm，该下降量包含了一系橡胶止挡间隙h0以及故障后止挡在构架压作用下的弹性变形，此时构架与轴箱的一系止挡销互相接触，一系刚度由橡胶垫提供；一位轮对右侧钢簧和二位轮对左侧钢簧均会有15 mm左右的下降，二位轮对右侧钢簧会有一定程度的上升，这是因为钢弹簧完全断裂，相当于自由端，车体向左侧倾斜，导致故障转向架左侧空气弹簧垂向力变大，该垂向力使断簧对角的钢弹簧产生上翘。

由图10可以看出：当前转向架左侧空气弹簧发生失气后，整车所有空气弹簧的位移均会发生变化，载荷也发生变化。其中，前转向架左侧空气弹簧首先下降了40 mm，该下降量包含了二系空气弹簧气囊间隙h1和故障后车体压力作用下的应急弹簧静变形，此时应急弹簧提供刚度支撑。在此基础上，由于车体质量较大，下移后对应急弹簧的冲击也较大，导致应急弹簧继续产生了9.78 mm的冲击变形，此时，二系空气弹簧下降至50 mm左右。左侧空气弹簧失气0.2 s后，右侧空气弹簧同样失气，由于左侧先于右侧接触到应急弹簧，故右侧应急弹簧产生的冲击变形比左侧小，其值为5.17 mm。失气后的1 s内，后转向架左侧空气弹簧会有一定程度的下降，同时，故障端对角的空簧高度产生一定程度的上升，失气1 s后，各空簧与应急弹簧进入稳定阶段。可见，前转向架左侧空气弹簧失气，对前端两侧空气弹簧变形量影响最大，对后端两侧空气弹簧影响较小。

图11和图12给出了钢弹簧断裂和正常工况下，2车前后车钩摆臂点处的高度变化。图13和图14给出了空气弹簧失气和正常工况下，2车前后车钩摆臂点处的高度变化。

图11 钢簧断裂下2车前车钩摆臂点处的高度

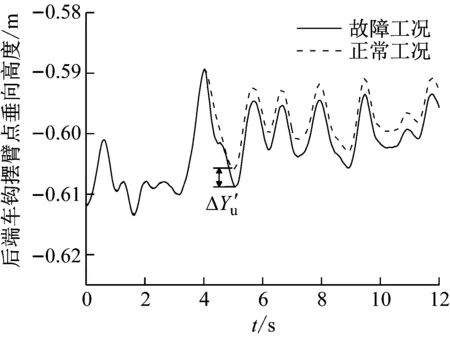
图12 钢簧断裂下2车后车钩摆臂点处的高度

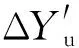
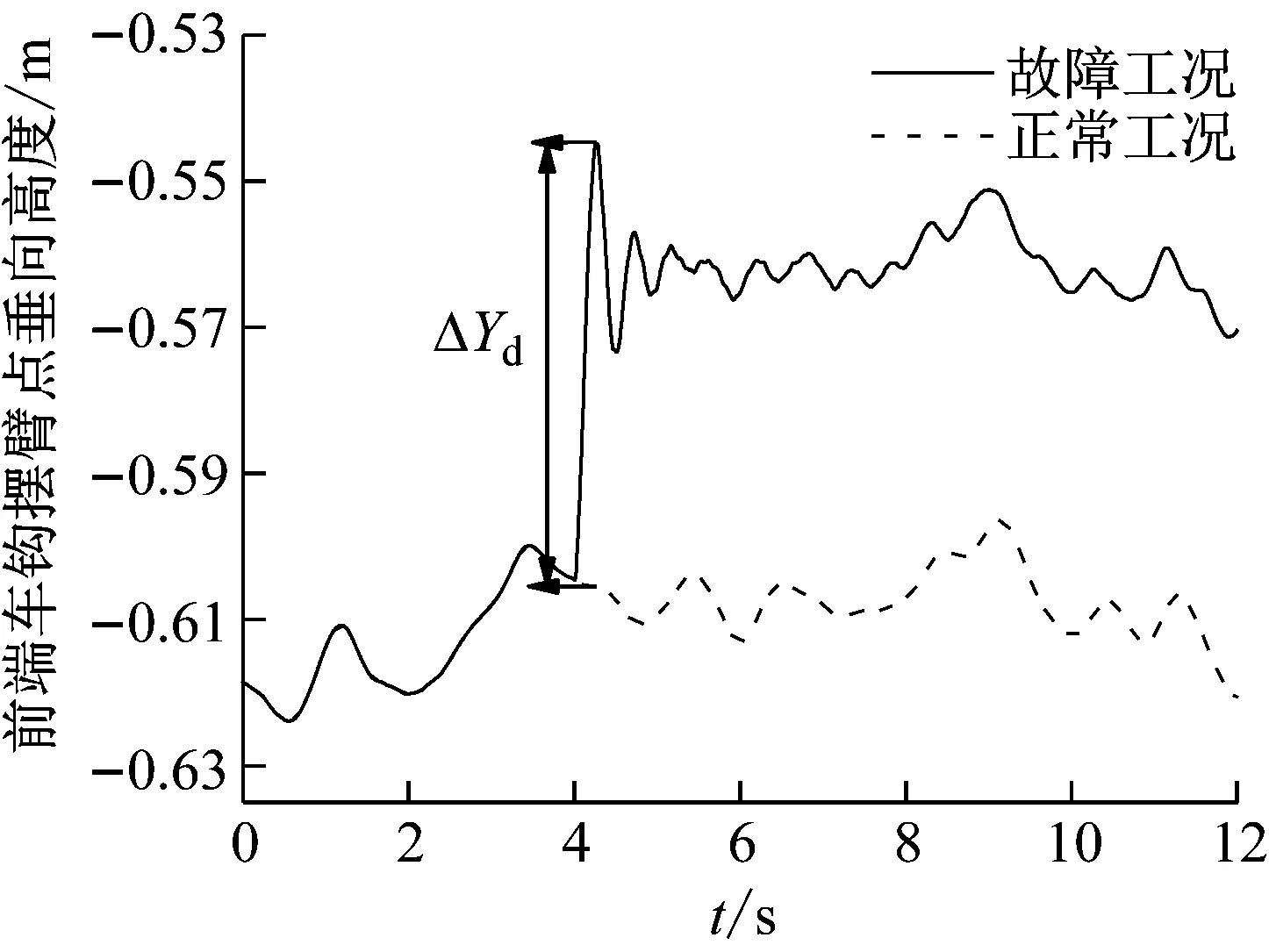
图13 空簧失气下2车前车钩摆臂点处的高度

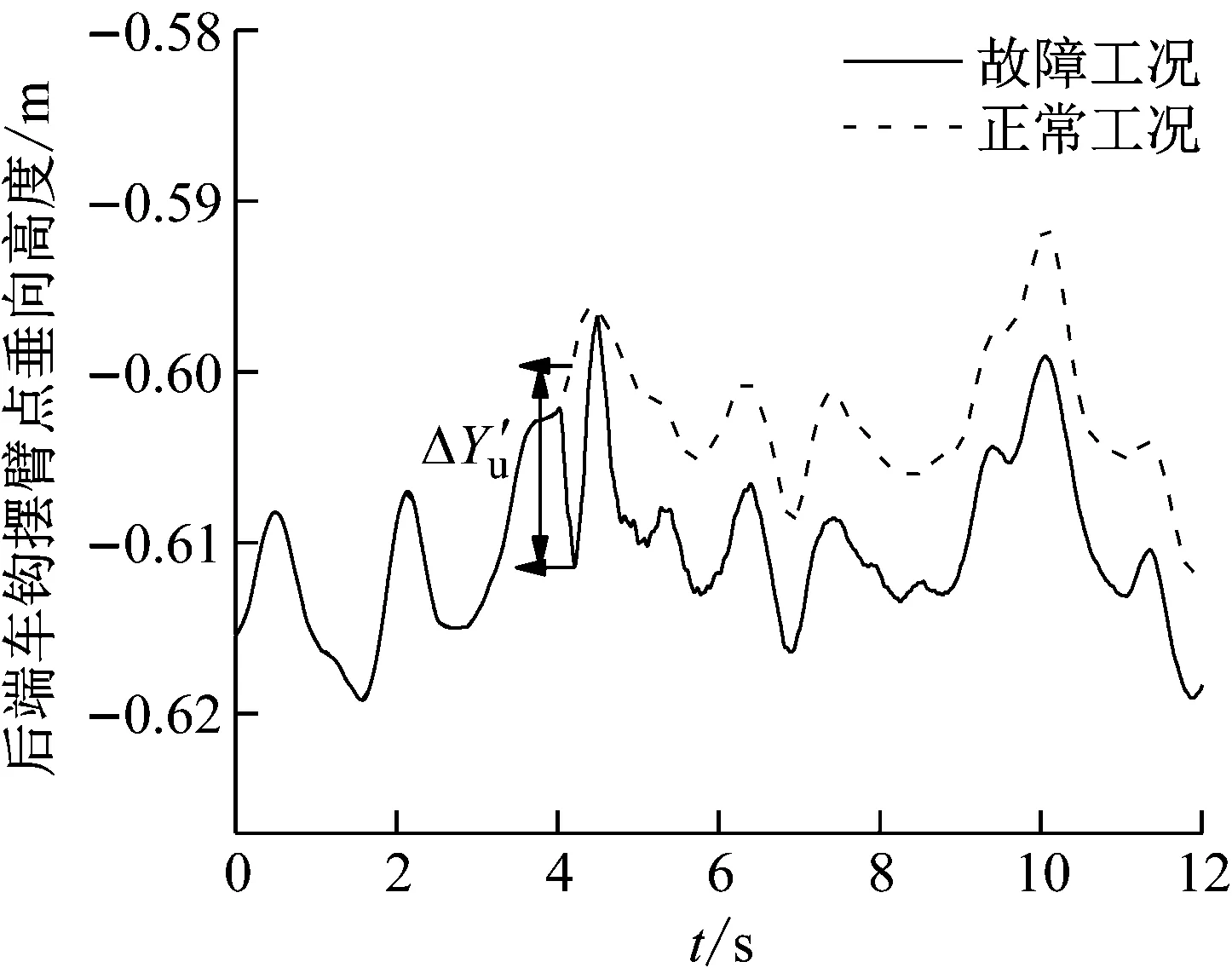
图14 空簧失气下2车后车钩摆臂点处的高度

2.3 车钩最大摆角分析

图15给出了考虑一系钢簧断裂和二系空气弹簧失气工况下，分别采用常规计算法、新方法(1.2节计算模型)的车钩最大摆角计算结果。其中，常规计算法中，一系断裂引起的一系悬挂下降量Δhps取40 mm，二系空簧失气引起的下降量Δhss取40 mm，均与仿真结果保持一致。

从图15可以看出:一系钢簧断裂时，本文提出的车钩计算模型的计算结果比常规计算法大1.2%，这是因为本文的新方法相比常规计算法多考虑了一系故障时车体柔性变形和各悬挂的变形。二系空气弹簧失气时，本文提出的车钩计算模型的计算结果相比常规计算法大10.2%，这是因为本文的新方法相比常规计算法多考虑了空簧失气时车体柔性变形、各空簧的变形和应急弹簧的冲击变形。对比一系、二系故障下的车钩最大摆角可以看出，不论采用哪种计算方法，二系空簧失气下的车钩摆角均大于一系钢弹簧断裂工况，其中，二系空簧失气工况相比钢簧断裂工况，两种方法的计算结果差异更加明显。

图15 故障工况下不同计算方法的计算结果对比

综上，在悬挂故障下，本文提出的车钩摆角计算模型相比常规计算法计算结果偏大，该方法可以充分考虑车体柔性，各部件装配、磨耗、制造误差和故障冲击下各悬挂变形等因素，故该模型有较好的实用性。

3 关键参数对车钩最大摆角的影响规律

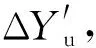
3.1 悬挂故障下降量对车钩摆角的影响

基于常规计算法，图16给出了悬挂故障下降量对车钩最大摆角的影响规律。

图16 悬挂故障下降量对车钩最大摆角的影响

从图16可以看出:在钢簧断裂和空簧失气两种工况下，随着悬挂下降量的增大，车钩最大摆角均呈变大趋势，且空簧失气下这种趋势相比钢簧断裂更加明显；钢簧断裂的下降量每增加5 mm，车钩摆角增大约0.086°，空簧失气的下降量每增加5 mm，车钩摆角增大约0.173°。依据2.2节仿真结果，当空簧失气时，应急弹簧将产生9.78 mm的冲击变形，这使得悬挂故障下降量瞬间达到49.78 mm，车钩摆角为5.37°，相比不考虑应急弹簧变形时的5.02°增大了7%。因此，在计算车钩最大摆角时，得到更为准确的悬挂故障下降量是十分重要的。

3.2 车体柔性变形对车钩摆角的影响

由2.1节仿真结果可以看出，当悬挂发生故障时，车体会产生垂向的柔性变形ΔhCT。基于本文提出的车钩最大摆角计算的新方法，给出了故障下车体柔性变形量对车钩最大摆角的影响规律，见图17。

图17 车体柔性变形量对车钩最大摆角的影响

从图17可以看出:车体垂向变形量ΔhCT越大，车钩最大摆角越大；当钢弹簧断裂与空簧失气时，车体垂向变形每增加1 mm，车钩摆角均增大约0.05°。依据2.2节仿真结果，当一系断簧发生时，车体产生0.18 mm的垂向变形，车钩摆角增大约0.009°，对车钩摆角影响极小；当二系失气时，车体产生1.6 mm的垂向变形，车钩摆角增大约0.08°，对车钩摆角整体影响仍然很小。综上，车体柔性变形对车钩最大摆角的影响有限，在计算中可以酌情考虑。

3.3 故障引起的摆臂点偏移量对车钩摆角的影响

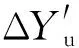
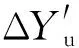
综上，悬挂故障下降量、车体柔性变形和故障引起的前后车钩摆臂点偏移量4个因素对车钩最大摆角均有一定影响，表明本文的新方法相比传统常规计算法考虑的因素更加全面合理，具有较好的实用性。

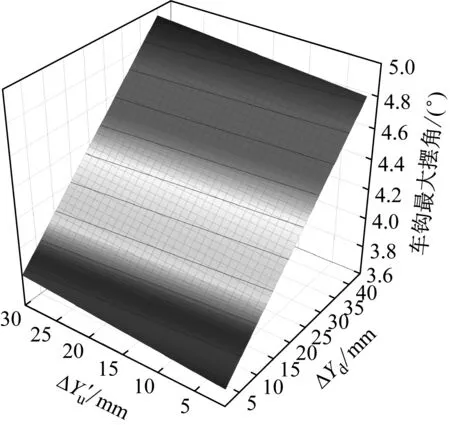
图18 故障引起的摆臂点偏移量对车钩摆角的影响

4 结 论

(1) 基于含悬挂故障的车辆动力学模型的车钩垂向最大摆角计算方法，可以发挥动力学仿真的优势，相比常规计算法，能充分考虑车体柔性、故障冲击下各悬挂变形等因素。相比常规计算法，单一钢簧完全断裂时，该方法计算结果偏大1.2%，单一空气弹簧失气时，该方法计算结果偏大10.2%。

(2) 针对该型地铁，当单一钢弹簧和单一空簧发生完全失效时，车体垂向变形分别为0.19 mm和1.55 mm，均不明显；两种故障发生时，悬挂会产生明显的冲击特性，此外，空簧失气时，应急弹簧也会产生明显的冲击变形，最大为9.78 mm；整车车体故障端高度降低，非故障端高度升高，车体姿态对故障端相邻车钩的垂向摆角产生不利影响。

(3) 钢簧断裂的下降量每增加5 mm，车钩摆角增大约0.086°，空簧失气的下降量每增加5 mm，车钩摆角增大约0.173°；车体垂向变形量ΔhCT每增加1 mm，车钩摆角均增大约0.05°；当非故障段车钩摆臂点向上偏移量、故障端车钩摆臂点向下偏移量都增大时，车钩垂向最大摆角将受两种偏移量的耦合作用，会更加恶劣。