固体火箭发动机变截面燃烧室纵向一维声模态特性研究

史晓鸣， 侯凯宇， 刘陆广， 高 阳， 夏 鹏， 李海东， 李莎莎， 陆丰玮

(1. 上海机电工程研究所， 上海 201109； 2. 上海航天技术研究院， 上海 201109；3. 上海航天动力技术研究所， 上海 201109； 4. 上海航天精密机械研究所， 上海 201600)

固体火箭发动机是运载火箭、导弹等细长体飞行器广泛采用的动力装置。不稳定燃烧是国内外固体火箭发动机研制中屡次遇到的难题[1-3]，其主要表现为发动机受扰动后，燃烧室内周期性压强振荡、平均压强改变，发动机输出推力振荡、平均推力及工作时长改变，并伴有发动机及飞行器的剧烈振动，严重时导致发动机熄火或超压爆炸，如图1所示。对于声不稳定机理的燃烧不稳定问题，是固体推进剂燃烧过程与燃烧室内声振过程相互作用的结果。而固体火箭发动机往往是细长体构型，燃烧室内纵向声模态频率远小于切向和径向，往往控制着燃烧振荡的发展[5]，因此研究纵向声模态对于固体火箭发动机的不稳定燃烧具有重要的意义！

经典的固体火箭发动机设计理论中常将燃烧室简化为等截面圆柱形，以当地燃气介质声速a和燃烧室长度L，根据理论解fn=na/2L计算第n阶纵向声模态固有频率。但对于翼柱型装药、双脉冲等真实发动机，在燃烧过程中其内部燃烧室截面变化复杂，理论解往往得不到准确的结果。文献[6-8]通过商业有限元软件对变截面燃烧室声模态的研究表明其纵向固有频率与等截面理论解存在较大差异，且高阶频率不再是一阶基频的整数倍。商业有限元软件通过对燃烧室三维几何模型划分网格进行数值计算可以精确分析复杂变截面燃烧室的声场特性，但每次燃烧室装药几何模型更改设计后都需要重新划分网格再进行数值计算。因此，三维有限元模型不适用于固体火箭发动机初始方案设计阶段的反复迭代优化及规律分析，更多的是用于最终设计状态确定后的校核。

图1 不稳定燃烧发动机燃烧室内压强

考虑到固体火箭发动机细长体构型特征，燃烧室内燃气流动可视作一维加质管道内流动问题。对一维管道内流体声压脉动研究是当前热点。Carmicino等[9]通过求解一维波动方程的解析解，研究了固液混合火箭在点火工作过程中燃烧室轴向声模态频率的变化规律。Li等[10]推导了环形燃烧室声场解析解，研究了非均匀截面和平均流场参数对声场特性的影响。Yeddula等[11]提出了变截面管道中的声波传播的半解析解。蔡建程等[12]理论分析了不可压缩流场压力脉动(伪声)与声波方程的区别，并在CFD(computational fluid dynamics)数值研究直管与弯管入口处设置简谐压力脉动条件下管内非定常流动的特性。赵天泉等[13]设计了声学试验发动机，通过试验研究前封头结构及潜入空腔对声稳定性的影响规律。

综上所述，在固体火箭发动机设计过程中，商业有限元软件可用于对三维燃烧室声场特性的精确校核，但在方案阶段的反复迭代优化设计上效率有所不足，且不便于直接分析截面变化对声模态影响机理规律；而一维模型计算效率高，且数学模型是个参数化模型，便于分析及理解其相关参数对纵向声模态的影响机理及规律。本文针对固体火箭发动机燃烧室纵向声模态准确高效分析以及变截面对声模态影响机理及规律研究的需求，建立考虑燃烧室截面面积变化的纵向一维声振方程，有限差分数值求解纵向声模态固有频率及振型，分析了截面变化对燃烧室纵向声模态特性的影响规律；通过变截面燃烧室模拟试验件的声模态试验获取脉动压力响应，基于解析模态分解和希尔伯特变换辨识纵向声模态参数，验证了本文数值方法的准确性；并进一步应用于固体火箭发动机燃烧工作过程中纵向声模态的数值仿真，分析其变化规律。

1 变截面燃烧室纵向一维声振方程

固体火箭发动机燃烧过程中，随着固体推进剂消耗，燃面不断退移，燃烧室空间逐渐扩大，且伴有生成燃气质量的注入，其所对应的声振系统是时变的。但声波在高温高压燃气介质内的传播速度远快于燃面退移和燃气生成质量注入的速度，因此可采用状态凝固化的思想，将连续时变系统在时间上分割为若干个短时时不变系统，提取发动机工作过程中若干时刻的燃烧室几何构型及该时刻的燃气参数开展声振分析。

固体火箭发动机工作过程中某一时刻变截面燃烧室内气体满足连续方程

(1)

动量方程

(2)

状态方程

(3)

式中：ρ为气体密度；A=A(x)为燃烧室截面面积；v为声波脉动速度；p为脉动压力；a为声速。

(4)

式(4)对t求导得

(5)

式(2)两端乘上截面面积A后对x求导得

(6)

(7)

(8)

(9)

2 有限差分法求解纵向一维声振模态

对于纵向长度为L的燃烧室，沿纵向均布N个截面，将燃烧室均分为N-1段，每段长Δx=L/(N-1)，第i(i=1～N)个截面上的面积及脉动压力分别记为Ai，pi。

在第2～第N-1个截面上均满足式(8)，由此可得N-2个方程

(10)

(11)

(12)

式(12)代入式(10)、式(11)后联立得矩阵形式的振动方程

(13)

式中：p={p1,p2,…,pN}T为脉动压力列向量；M，K分别为声质量、声刚度矩阵。解广义特征值(K-λM)·φ=0得声振模态。

(14)

(15)

图2 截面积阶梯突变

以及脉动速度与脉动压强的关系

(16)

可得

(17)

式(17)表明，脉动压强对纵向坐标的偏导数在面积阶梯突变截面的两侧不连续，截面两侧的偏导数与两侧的面积成反比。

(18)

式(18)代入式(17)得

4pi+1-pi+2)

(19)

式(19)替换式(13)中的第i行即可。

3 试验验证及声模态辨识方法

真实固体火箭发动机点火试车试验成本巨大，且搭载高温高压燃气工况下声模态试验具有危险性。为验证本文方法的准确性，设计了若干截面为圆形但截面面积沿纵向变化的燃烧室模拟试验件，如图3所示。包括截面半径线性变化、截面积指数变化、截面积阶梯突变、局部截面收缩等4组工况，用于模拟翼柱型装药、双脉冲等真实固体火箭发动机中可能存在的各类截面变化情况。试验件材料为2A12铝合金，加工过程中，各试验件一端已一体成型密封，另一端预留开口用于安装喇叭，沿外表面一条母线钻麦克风传感器安装孔，孔的位置及数量见图3，截面半径线性变化、截面积指数变化工况均为3个孔，截面积阶梯突变、局部截面收缩工况均为5个孔，麦克风传感器编号以最靠近开口端的位置为“1#”，依次递增类推。

(a) 截面半径线性变化

(c) 截面积阶梯突变

进而开展了一个标准大气压下常温大气介质(声速a=343 m/s)的纵向声模态试验。试验系统及现场照片，如图4所示。模拟试验件放置于海绵垫上，在开口端安装HiVi-Q3喇叭并嵌入O型圈密封，沿外表面母线预留孔安装Microtech Gefell MM210麦克风传感器并以硅胶密封，Lms.SCR05数据采集器输出猝发随机信号，通过DPM200A功率放大器驱动喇叭对试验件内气体介质施加声激励，数据采集器同时采集麦克风传感器感受到的脉动压力信号。

图4 试验系统及现场

试验过程中喇叭实际对试验件内气体介质的声激励输入不可测，只通过麦克风传感器获取了声振脉动压强响应。本文采用基于希尔伯特变换的解析模态分解和振动系统辨识方法从响应数据中识别声模态参数。

对猝发随机激励下产生的自由衰减脉动压强信号FFT(fast Fourier transform)后得声振系统频谱图，如图5所示。图5中前3阶谐振峰清晰易识别，表明本文对模拟试验件采用猝发随机激励产生自由衰减脉动压强信号的信噪比良好。以此确定各阶声振谐振频率ωi,i=(1,2,…,n)。应用解析模态分解方法[14]，选取若干二分频率ωbi∈(ωi,ωi+1),i=(1,2,…,n-1)，将脉动压力信号x(t)表示为若干个单频信号xi(t)的叠加

xi(t)=si(t)-si-1(t)，

s0(t)=0，

si(t)=sin(ωbit)H[x(t)cos(ωbit)]-

cos(ωbit)H[x(t)sin(ωbit)],

i=1,2,…,n-1

(20)

式中：H·为希尔伯特变换；si(t)为频率小于ωbi∈(ωi,ωi+1),i=(1,2,…,n-1)的信号，即低通信号；xi(t)即为本征模态信号。典型的自由衰减脉动压强信号经解析模态分解后的本征模态信号，如图6所示。各麦克风传感器位置上的同一阶本征模态信号周期相同，振幅及相位不同，对其进一步分析即可识别模态参数。

对每一阶本征模态信号xi(t)应用基于希尔伯特变换的振动系统辨识方法[15-16]识别模态参数，系统第i阶固有圆频率ωi(t)表达式为

(21)

式中：A(t)为瞬态幅值或称包络线；ω(t)为信号的瞬态频率。

图5 声振系统频谱图

(a) 1阶

(b) 2阶

(c) 3阶

对于声阻尼较小的系统，系统第i阶声模态在第a个传感器测点上的振型可以表示为

Sia=Aai(t)cosψi/Abi(t)

(22)

式中：Aai(t)，Abi(t)分别为a，b两个测点上的第i阶本征模态信号的包络线；ψi为a，b两个测点上的第i阶本征模态信号的相位差。

4 结果与讨论

4.1 变截面燃烧室模拟试验件纵向声模态

变截面燃烧室模拟试验件纵向声模态频率采用本文方法计算、有限元软件ABAQUS三维实体模型仿真以及试验结果及其对比误差，如表1、表2所示。从表1、表2中可见：本文方法与有限元仿真及试验的结果比较均非常接近，截面半径线性变化、截面积指数变化两种工况下的计算与试验结果误差略微大于截面积阶梯突变、局部截面收缩两种工况下的计算与试验结果误差。这是由于麦克风传感器安装时，其咪头需略突出于内表面以充分感受到压强脉动，从而引起该安装截面上的截面积局部小幅度突变，导致试验与仿真结果之间存在误差，如图7所示；但在截面积阶梯突变、局部截面收缩两种工况下，试验件本身存在较大幅度的局部截面积突变，故麦克风安装引起的局部截面积变化对试验结果的影响反而不明显。

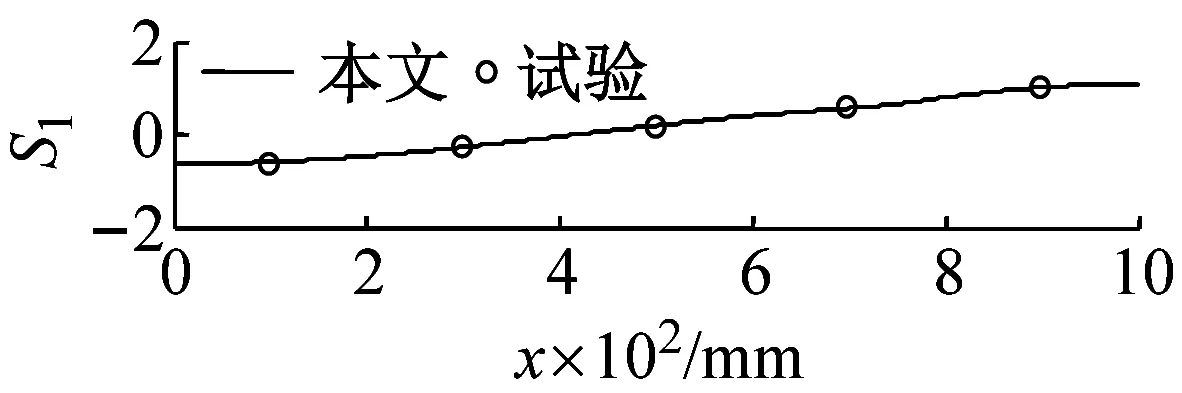
从表1中可见，变截面试验件第n阶(n>1)纵向声模态频率fn与 1阶基频f1之间的关系fnf1≠n，而是n-1

前3阶纵向声模态振型S1，S2，S3如图8所示。图8中左端对应封闭端，右端对应开口安装喇叭端。本文约定以1#麦克风传感器所在位置的振型为1进行归一化，该位置在图8各个图中均为最右侧的试验测点。变截面工况下，纵向声模态的奇数阶振型关于纵向长度的中点不再保持反对称，偶数阶振型关于纵向长度的中点不再保持对称：以与燃烧振荡密切相关的一阶声模态为例，截面半径线性渐变、截面积指数变化、截面积阶梯突变等变截面工况的纵向声模态振型的最大幅值均出现在截面积较小的一侧端面，同时其振型节点位置与等截面振型节点相比，不再处于纵向长度的中点位置，而是从中点向截面积较大的一侧移动；局部截面收缩变截面工况的纵向声模态振型的最大幅值出现在中间收缩段的一侧端面，同时其振型节点位置与等截面振型节点相比，不再处于中点位置，而是从中点向局部收缩段的一侧移动。这是由于在变截面模拟试验件内为同一气体介质，气体介质体积模量K是均匀分布的，但截面积A(x)沿着纵向变化，故各个截面上的气体介质拉压刚度K·A(x)沿着纵向分布是不同的，截面积较大区域其拉压刚度较大，脉动声压的振型幅值会较小，由此必然造成节点两侧的振型不再保持对称或者反对称。

表1 纵向声模态频率

表2 纵向声模态频率结果误差

图7 麦克风传感器咪头安装示意图

4.2 固体火箭发动机燃烧工作过程中纵向声模态

进一步将本文方法应用于某内孔型装药真实固体火箭发动机燃烧工作过程中的纵向声模态分析。取整个工作过程中归一化时间tn=0，1/3，1/2，2/3，1共5个时刻的燃烧室几何构型开展纵向声模态分析。前3阶纵向声频率变化规律，如图9所示。在发动机工作的初始阶段，其纵向声模态频率明显小于等截面状态下的频率；随着发动机燃烧工作直至熄火，纵向声模态频率逐渐单调上升趋向于等截面状态下的频率，直至最终接近等截面状态下的频率。

图9 固体火箭发动机燃烧工作过程中纵向声模态频率

图10 固体火箭发动机燃烧工作过程中燃烧室截面积变化

5 结 论

(1) 本文推导了考虑燃烧室截面面积变化的纵向一维声振方程，有限差分数值求解纵向声模态固有频率及振型；设计了变截面燃烧室模拟试验件，以声模态试验验证了本文数值方法的准确性。

(2) 变截面燃烧室模拟件试验表明：变截面工况下，纵向声模态频率第n阶(n>1)纵向声模态频率fn与 1阶基频f1之间的关系fnf1≠n，而是n-1

(3) 对于内孔翼柱型装药结构的固体火箭发动机，在发动机初始工作阶段，截面变化最为剧烈，工程中常用的将燃烧室简化为等截面圆柱分析方法误差较大，此时必须考虑截面变化的影响，从而得到更为准确的声模态。