非电起爆网路修正单响药量计算及PPV预测应用实例

何 理， 杨仁树， 钟冬望， 解联库， 张 奎， 杨 磊

(1. 武汉科技大学 冶金工业过程系统科学湖北省重点实验室， 武汉 430065； 2. 北京科技大学 土木与资源工程学院， 北京 100083； 3. 矿冶科技集团有限公司，北京 100160；4. 湖北皓昇爆破工程有限公司， 湖北 十堰 442012； 5. 武汉建工市政工程有限公司， 武汉 430000)

通过选用合适的起爆系统和合理的延期时间，可有效减小爆破振动强度、改善岩石破碎效果、减小爆破飞石及噪声等不利影响[1-4]。导爆管起爆系统由于成本低廉、使用简便、分段灵活、不受杂散电流影响，现阶段仍然是爆破从业人员的首选，被广泛应用于矿山开采、水利水电工程建设中。爆破工程实践中，质点峰值振动速度(particle peak vibration velocity,PPV)通常被认为是衡量爆破施工作业对周边环境影响的主要指标。而PPV主要受最大单响药量、监测点距爆炸中心的距离(爆心距)及施工现场地质条件等因素影响。在场地地质条件客观不可改变的情况下，最大单响药量和爆心距是主要的可控参数。由于爆破振动的不利影响，准确预测爆破震动速度并分析其衰减规律具有重要意义[5-6]。然而，导爆管雷管延时精度低、延时误差较大，且随雷管段别增加误差逐渐增大[7-8]，致使在非电起爆网路中同段齐发炮孔的起爆时刻存在离散现象，并非“同时刻”起爆。同时，当孔内使用高段别雷管起爆、孔外使用低段别进行接力传爆时，可能出现相邻段别炮孔起爆时刻重叠或后续炮孔先起爆的情况，造成分段爆破振动叠加现象，本质上表现为实际单响药量增加而大于设计值，从而造成地表质点振速水平超标。因此，在分段繁多的大规模微差爆破中，因雷管延时误差引起的同段齐发炮孔起爆时刻离散效应及分段爆破振动叠加现象不容忽视。

针对雷管延时误差引起的分段爆破振动叠加现象，有学者提出了叠加情况下等效单响药量的取值方法[9-11]，然而利用现场爆破振动实测数据进行回归分析时，回归分析的相关性并不高，爆破振动峰值计算误差很大[12]。基于此，Hemant等[13-14]基于大量实测数据的统计回归分析，在PPV预测公式中引入振波叠加因子，体现了分段振波叠加对PPV的影响，提高了预测精度。然而大量实践数据与研究表明[15]，同段毫秒雷管延期时间的密度分布是服从正态分布，每发雷管的实际延时在其置信区间是随机分布的，采用确定性分析方法来研究雷管延时误差引起的爆破振动叠加问题较为困难。因此，许红涛等[15]借助遗传算法研究得到了因雷管延期误差引起爆破振动速度叠加的最大可能放大倍数，以此来评价雷管延期误差带来的危害性，并提出可参考放大倍数对单段齐爆药量进行折减。另外Hemant等[16]通过概率统计方法系统分析了炮孔起爆时刻重叠对非电起爆网路单响药量的影响规律，但却是将雷管延时误差看作均匀分布进行处理，并未考虑雷管延时误差的正态分布特性。此外，韩亮等[17]利用数理统计方法分析雷管延时误差对双孔爆破叠加干扰的影响，指出低段位雷管降振概率受测点距离影响比高段位雷管大，得到了MS10～MS15段雷管的延期误差概率。李峰利用正态分布概率模型分析得到了逐孔起爆网路中25 ms( MS2)，50 ms( MS3)能够提高地震波干扰降振的概率，避免多孔齐发、后排先爆现象的发生。

纵观以往研究成果，尚未有效分析并揭示雷管延时误差对炮孔起爆时刻重叠的影响规律，同段齐发炮孔起爆时刻离散效应造成的该段等效药量取值问题有待进一步明确，较少有综合考虑同段齐发炮孔起爆时刻离散及分段爆破振动叠加双重因素的研究成果，深入研究该课题具有重要的现实意义。

考虑雷管延时误差服从正态分布的特性，基于概率理论分析雷管延时误差对非电起爆网路炮孔起爆时刻与重叠程度的影响规律，构建炮孔同时起爆的概率计算模型；研究同段齐发炮孔起爆时刻的离散效应及等效药量取值方法，在此基础上创新性提出非电起爆网路修正单响药量的概念及计算方法，并将修正单响药量用于施工现场振速模型回归分析及PPV预测，研究成果对爆破振动速度预报及控制具有指导意义。

1 非电起爆网路炮孔同时起爆的概率计算模型

非电起爆网路由于装药的空间分布、时间延迟和分段振波叠加影响，每延迟的准确单响药量是未知的，测点PPV所对应的真实单响药量也不得而知。因此，起爆网路的实际单响药量与爆破设计严重不符。若仅仅依据起爆网路设计统计最大单响药量和爆破振动速度峰值，很难确保最大单响药量一定对应出现最大爆破振动速度，这样的简单统计方法会遗漏掉大量的振动分析信息，导致回归分析相关性差，甚至可能回归出奇异的场地条件相关系数[18]。

为降低爆破振动和改善岩石爆破效果，非电起爆网路通常孔内使用高段别雷管、孔外使用低段别雷管进行传爆。文中以图1所示典型非电起爆网路为例，分析雷管延时误差对炮孔起爆时刻及其相互重叠程度的影响规律。

图1 典型非电起爆网路

图1非电起爆网路包含30个炮孔，共计10排，同排3个炮孔采用簇联形式接入传爆网路。孔内均选用MS11段雷管起爆药包，排(段)间选用MS3段雷管进行传爆。

1.1 炮孔实际起爆时刻的概率分布

国内生产的导爆管雷管延时误差，如表1所示。

表1 雷管延时误差

由表1可知，随着雷管段别的提高，雷管延时偏差呈现逐渐增大趋势，因此其起爆时间窗口的范围也在不断扩大，爆破工程师对雷管实际起爆时刻的掌控力逐渐降低。因此，要对毫秒延时爆破PPV进行准确预报，必须考虑雷管段别与雷管延时误差对起爆网路实际单响药量的影响。针对图1所示非电起爆网路，将第i排炮孔的最早起爆时刻和最迟起爆时刻分别计为T早，i，T迟，i，将第i排炮孔的名义起爆时刻计为t名，i，则T早，i，T迟，i和t名，i可分别计算如下

(1)

t名，i=i×N3+N11

(2)

由于各排炮孔实际起爆时刻在起爆时刻区间内服从正态分布，因此各排炮孔实际起爆时刻的概率分布，如图2所示。

由图2可知，由于传爆支路的延时误差累积，经多段延时接力后，后爆炮孔的实际起爆时刻区间范围越来越宽，各炮孔实际起爆时刻随机性更大。邻近段别炮孔起爆时刻区间的叠加程度随之增大，从而引起显著的分段爆破振动叠加现象。邻近段别炮孔起爆时刻重叠或后序炮孔先爆的概率随之增加，实际起爆时刻与名义起爆时刻趋于一致的可能性逐渐降低。此时，实际单响药量往往大于设计值，若仍然按照最初爆破设计的单响药量取值并进行统计分析，显然是不科学的。

表2 各排炮孔名义起爆时刻及方差

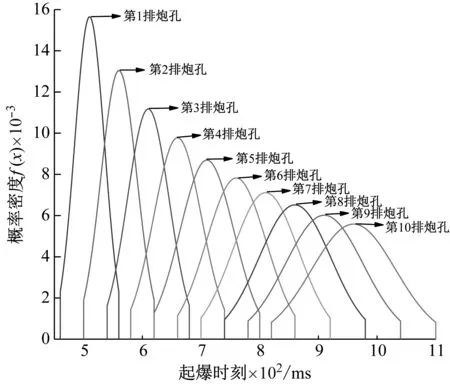
图2 各排炮孔实际起爆时刻的概率分布图

1.2 相邻炮孔同时起爆的概率计算方法

为定量计算非电起爆网路中多排炮孔同时起爆的概率，根据正态分布概率密度图的定义可知，计算相邻炮孔同时起爆的概率即求正态分布曲线重叠区域的面积，如图3所示。

(a) 相邻2排炮孔同时起爆

(b) 相邻n排炮孔同时起爆

由图3可知，后爆(排)炮孔实际起爆时刻的区间范围越来越大，受孔外传爆接力雷管延期时间和雷管延时误差双重作用的影响，后爆(排)炮孔最早起爆时刻T早，i+n-1不断后移，逐渐逼近前排(第i排)炮孔的最迟起爆时刻T迟，i，当炮孔排数较多时甚至会晚于第i排炮孔的最迟起爆时刻T迟，i。因此，相邻的n排炮孔起爆时刻区间产生重叠区域的面积，会随着n值的增大而相应减小。

基于上述分析，可得到相邻n排炮孔同时起爆的概率Pn通过下式进行计算

(3)

通过式(3)可计算得到相邻n排炮孔同时起爆的概率Pn，如表3所示。

由表3可知，各排炮孔很难严格按照名义起爆时刻依次顺序起爆，多排炮孔同时起爆的概率较大，分段地震波相互间的干扰叠加现象难以避免，印证了1.1节分析讨论结果。

进一步地，Pn在传爆网路中的分布情况，如图4所示。

由图4可知，由于传爆网路的延时误差累积，导致多排炮孔同时起爆概率的大值多集中在传爆网路的中后期。因此爆破工程实践中，可通过降低单次爆破规模、缩短起爆网路传爆路径、减少延期雷管数目等方法改善非电起爆网路重段、跳段现象。

表3 相邻n排炮孔同时起爆的概率

图4 Pn在传爆网路中的分布情况

根据表3依次可计算得到n排炮孔同时起爆的平均概率，如图5所示。

图5 n排炮孔同时起爆的平均概率

由图5可知，相邻2排炮孔同时起爆的概率最大，达到0.48，各排炮孔依次独立顺序起爆的概率仅为0.47，表明起爆网路实际最大单响药量增高是大概率事件。

将图5中n排炮孔同时起爆事件xn视为一系列离散型随机变量，则随机变量值及概率如表4所示。

则同时起爆炮孔排数的数学期望E(x)通过下式[19]计算

(4)

表4 随机变量值及概率

计算得到图1非电起爆网路同时起爆炮孔排数的期望值

E(x)=1×0.47+2×0.48+3×0.20+4×0.07+

5×0.01=2.35(排)

2 齐发爆破等效药量取值方法改进

炸药爆破会引起岩土体高度非线性响应，Blair[20]依据比例药量法则，提出了单孔爆破振动速度的非线性叠加方法，如图6所示。

图6 非线性叠加方法示意图

图6炮孔中药包质量为Q总，可分为M个药包单元，各药包单元质量q=Q总/M，炸药量q在O处激发的VPP，n可用式(5)计算[20]

VPP，n=k{(nq)α-[(n-1)q]α}

(5)

式中：n为药包单元编号，n=1～M；k，α为与现场地质条件相关的系数，与爆破方式、装药结构、爆破点至监测点间的地形、地质条件密切相关。

因此，VPP，1=kqα。当R≫(l1+l2)时，R=Rn，则图6单孔爆炸在O处(爆心距为R)引发的PPV为

(6)

通过式(6)可分析得到，由于炸药爆速通常可达5 000 m/s以上[21]，单个炮孔内整个装药段完成爆轰所需时间极短，各药包单元可近似为同时刻起爆，此时段药量可取为各药包单元的算数和。然而，由于雷管延时误差客观存在，群孔齐发爆破时各炮孔存在起爆时刻的不确定性，同时地震波传播路径及爆心距等差异也会影响爆炸地震波传播到振速观测点的时间，势必都会引起各孔爆炸地震波之间的错峰现象，导致观测点处PPV水平偏低。因此群孔齐发爆破时等效药量取这些炮孔装药量的算术和不合理。

Singh等[22]通过现场试验研究提出，群孔齐发爆破时通过对炮孔数目N取立方根或平方根，从而折算等效药量，可使得PPV回归分析误差最小化，但并未明确何时取小值、何时取大值进行炮孔数目的折算处理。基于此，本文试图引入缩比因子η对群孔齐发爆破孔数N进行缩比处理，进而对群孔齐发爆破等效药量取值方法进行改进。

根据概率理论分析可知，齐发爆破孔数N越大，所有炮孔在同一时刻起爆的概率越小，由此根据式(6)可计算得到观测点处的振动合速度越小，对应的齐发爆破等效药量值就越小，因此炮孔数目的缩比因子η应该越小。生产爆破实践中，通常选用双发雷管绑扎不超过20根导爆管(20个炮孔)实现群孔齐发爆破，即齐发爆破炮孔数2≤N≤20。因此，假设缩比因子η满足如下关系式

η=A×BN

(7)

式中，A，B为待定系数。

根据本节分析可知，式(7)具有边界条件

(8)

联合式(7)、式(8)可计算得到待定系数A，B的值，进而得到缩比因子η的计算公式

η=0.523×0.978N

(9)

因此，群孔齐发爆破时等效药量可按照下式进行取值

(10)

3 修正单响药量概念及计算方法

修正单响药量是非电起爆网路中同时起爆炸药量的理论期望值，也是起爆网路在传爆过程中的实际单响药量，其大小直接影响毫秒延时爆破时地表PPV水平。根据1.2节分析可知，依据爆破设计可计算非电起爆网路中同时起爆炮孔排数的数学期望；同时，考虑同段齐发炮孔起爆时刻的离散效应，需要对炮孔数目进行缩比处理。因此，得到修正单响药量QM计算公式

(11)

对于不同的非电起爆网路设计，会使用不同的地表传爆雷管与孔内起爆雷管的组合形式，由此造成分段地震波间不同程度的叠加，导致同时起爆炮孔排数的数学期望值并非定值，此时需利用同时起爆炮孔排数的概率计算模型(probability calculation model,PCM)重新计算E的值。

4 基于修正单响药量的PPV预测应用实例

4.1 爆破振动速度模型及预测精度评价指标

在无需考虑高程差因素对爆破振动传播的影响时，通常选取如下形式的PPV预测模型[23-24]

(12)

式中：Q为最大单响药量，kg；SQ为比例药量，kg1/3m；其余同前。

选用拟合相关系数(R2)、均方根误差(root mean squared error,RMSE)和平均相对误差(absolute relative error，ARE)作为模型预测精度的量化指标，计算公式[25]如下

(13)

(14)

(15)

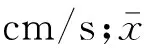
4.2 舟山石油储备基地扩建工程

舟山石油储备基地扩建工程地处浙江省舟山市岱山县临城新区岙山岛西北部，设计规模为300万m3，布置10万m3储油罐30个。场区建设涉及山体边坡开挖与下穿隧道掘进，边坡共分9级放坡，每级平台宽度3 m，山体表面多为黏土或粉质黏土，厚度不等，往下分别为全风化、强风化、中风化、微风化晶屑玻屑凝灰岩，大部岩体中等硬度，可爆性和可钻性都较好。现场生产爆破炮孔直径为115 mm，采用2#岩石乳化炸药，装药结构为连续装药，梅花形布孔形式。爆破设计参数与振动监测信息，如表5所示。

表5 爆破设计参数与振动监测信息

起爆网路延期方案与装药设计，如图7所示。

图7 起爆网路延期方案与装药设计(名义延期时间单位ms，炮孔装药量单位kg)

图8 PPV随SQ的变化曲线

由图8可以看出，爆破振动速度预测模型回归拟合效果良好，相关系数R2=0.954，进一步统计得到预测值与监测值间ARE为5.2%，RMSE为0.59 cm/s。

4.3 十堰堰口露天采场项目

堰口采石场地处湖北省十堰市茅箭区朝北沟，矿区面积0.059 1 km2，矿区属构造侵蚀剥蚀低山山坡与丘陵交接部位，沟谷发育，地表切割较强烈，地层及岩性简单，矿体主要成分为晋宁期辉绿岩，岩石裂隙不发育，且大部分裂隙呈闭合状态。现场生产爆破炮孔直径为105 mm，炮孔主爆药选用岩石膨化硝铵炸药，2#岩石乳化炸药为起爆药，段间采用MS2段雷管(25 ms)进行传爆，以取得良好的破岩效果。爆破设计参数与振动监测信息，如表6所示。

表6 爆破设计参数与振动监测信息

起爆网路延期方案与装药设计，如图9所示。

图9 起爆网路延期方案与装药设计(名义延期时间单位ms，炮孔装药量单位kg)

统计得到PPV预测值与监测值间ARE为8.5%，RMSE为0.85 cm/s。

5 分析与讨论

图9与图10中爆破振动监测数据拟合相关性分别达到0.95和0.92，说明选用修正单响药量回归爆破振动速度模型回归拟合效果好，同时PPV预测值与监测值间ARE分别为5.2%，8.5%，RMSE分别为0.59 cm/s，0.85 cm/s，表明修正单响药量用于PPV回归分析及预测具有较高精度，用于爆破振动速度预测是可行的。

在某一特定场地条件下，选用不同起爆系统或者取值不同的单响药量统计回归出的爆破振动速度模型是不同的，各模型公式中场地条件相关系数(k，α)间往往存在较大差异[26]，这与现场场地条件的客观不可改变性是相互矛盾的。从振动速度公式场地条件相关系数的物理意义出发，当施工现场地质、地形条件一定，且不改变装药结构和爆破方式的情况下，理论上爆破振动速度模型的场地条件相关系数不会随起爆系统或爆破次数改变而发生变化。因此，在同一施工现场，可首先通过单孔爆破试验数据回归分析得出施工现场爆破振动速度模型，在后续生产爆破时，依据本文建立的方法计算得到非电起爆网路的修正单响药量，代入单孔爆破振速回归模型即可对PPV进行准确预测，大大降低长期监测的成本及费用。

图10 PPV随SQ的变化曲线

不同的雷管制造厂由于配方、工艺方面的差异，所生产雷管的延时特性将会有较大差异。表1中给出的毫秒延期雷管延时误差，是分批抽检雷管延期时间得到的延时偏差在95%置信区间的统计数据。针对某特定工程在实施生产爆破前，可尝试利用高速摄影法及光电法[27]抽样测试同批次雷管延时特性，进而结合爆破设计进行修正单响药量的计算。另外，导爆管的传爆速度约为2 000 m/s，导爆管传爆耗时会对各炮孔的起爆时间与顺序产生一定影响，后续研究需要考虑导爆管长度对分段爆破振动叠加的影响。针对同段齐发炮孔等效装药量的取值，本文提出利用缩比因子η对炮孔数目进行折算处理得到，然而在炮孔装药量和排(段)间炮孔数目差异较大情况下，如何进行取值则有待进一步深入研究。

6 结 论

(1) 传爆网路的延时误差累积，造成后爆炮孔起爆时刻区间逐渐变大，邻近段别相互叠加干扰程度随之增加，引起显著的分段爆破振动叠加现象，导致非电起爆网路实际单响药量大于设计值。

(2) 构建了非电起爆网路同时起爆炮孔排数的概率计算模型，计算得到孔外MS3传爆、孔内MS11起爆的网路同时起爆炮孔排数的期望值为2.35，孔外MS2传爆、孔内MS9起爆的网路同时起爆炮孔排数的期望值为4.67；齐发炮孔起爆时刻存在离散效应，导致齐发爆破时等效药量比炮孔装药量的算术和小，可利用提出的缩比因子计算方法折算齐发炮孔数目计算得到。

(3) 创新性提出了修正单响药量概念及计算方法。工程应用表明，选用修正单响药量回归爆破振动速度模型拟合效果好，PPV预测精度高，而且可依据同一振速模型对不同爆破次数时PPV进行预测，节约振动监测成本；相较于电子雷管起爆，采用非电起爆网路联网方便，成本大幅降低，研究成果对复杂环境下爆破振动的严苛控制和低成本施工具有指导意义。