冰-车-桥系统耦合振动分析

吴甜宇， 邱文亮

(1. 重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室， 重庆 400074;2. 大连理工大学 建设工程学部， 大连 116024)

渤海是我国纬度最低的结冰海域，冬季及初春开化时期会形成特有的流冰现象，渤海海域跨海桥梁的建设与运营将面临冰荷载的严峻挑战。因此，桥梁结构在车辆和冰荷载共同作用下的振动分析以及行车安全分析已成为寒区结冰海域桥梁建设不可回避的研究课题。

随着桥梁跨径的增大和汽车轴重的增加，公路桥梁上的车-桥相互作用问题越来越突出。自20世纪70年代以来，随着有限元方法的发展和计算机在土木工程中的应用，车-桥相互作用理论已经发展到包括复杂的车辆模型、桥梁模型以及路面粗糙度模型。对于车-桥耦合研究方向的发展历程来看，学者们提出了许多模型研究交互系统的动态响应。Yang等[1]采用结构动力缩聚方法将车辆的自由度缩聚到相应的桥梁上，从而求解车-桥相互作用系统的积分方程。该法是计算桥梁响应的有效方法，但它不足以计算车辆响应。Neves等[2]开发了一种有效的车-桥耦合计算方法，在该算法中车辆和桥梁的控制方程与附加的约束方程相互补充，约束方程实现了车辆接触节点位移与桥梁相应节点位移的耦合作用。Lu等[3]利用罚函数定义车桥接触条件，提出了基于有限元软件ABAQUS的车-桥相互作用系统的动力分析框架，实现了车-桥相互作用的仿真模拟。通过对比分析，发现数值结果与Yang等[4]提出的经典车-桥相互作用问题的解析解吻合很好，证明了该方法的正确性。

此外，许多研究学者对考虑不同影响因素的车-桥耦合振动分析开展了针对性的研究。夏超逸等[5-6]建立了撞击荷载作用下的车-桥耦合系统动力分析模型，提出了一种适用于车-桥动力耦合系统的时程积分全过程迭代法，系统地研究了撞击荷载类型、撞击强度、列车速度等对桥上列车运行安全指标的影响规律，给出了撞击荷载作用下保障桥上列车运行安全的撞击强度-列车速度阈值曲线的确定方法。乔宏等[7]基于子结构方法，将完整的列车-桥梁-桩基-地基相互作用模型分解为列车-桥梁相互作用子系统和桩基础相互作用子系统，研究了桩土相互作用对车桥耦合系统动力响应的影响。谢娟娟等[8]建立了随机汽车-桥梁耦合模型，采用路面谱对路面不平顺进行模拟转换，引入概率密度演化方法，对考虑路面不平顺随机性的汽车过桥动力响应进行了分析。Camara等[9]提出了考虑桥面粗糙度随机特性的风-车-桥耦合分析框架，进行了风荷载作用下桥上行车安全性及行车舒适性风险分析。Li等[10]研究了地震作用下高墩连续钢构桥梁车-桥相互作用系统的动力反应，探讨了地震动、地面峰值加速度值、桥墩高度、车速等参数对车辆和桥梁动力响应的影响。

综上所述，虽然目前车-桥耦合振动分析已经取得了较多的研究成果，但是对于冰荷载作用下的车-桥耦合振动研究还比较缺乏。因此，本文提出了冰-车-桥系统耦合动力分析框架，系统的研究了冰荷载作用下桥梁和车辆的动力反应，分析了不同车速和冰速对桥上行车安全的影响。本文研究成果可为冰荷载作用下寒区海域跨海桥梁的行车安全评估提供参考。

1 冰-车-桥系统耦合动力分析框架

1.1 车辆模型

本文采用的车辆模型是典型的两轴六轮载重卡车，每辆卡车都被视为一个具有12个自由度的动力学系统，其中车辆模型为一个质量-弹簧-阻尼体系，包含一个车体和两个轮轴，前轮轴包括一个轮对，后轮轴包括两个轮对，如图1所示。车辆悬挂系统和车轮采用弹簧进行建模，利用黏滞阻尼模拟悬挂和车轮的能量耗散过程，悬挂和车轮的质量均集中在车体的质量上，卡车特征参数详见文献[11]。卡车模型的动力学系统可以利用下面的广义位移矢量进行表示

wv={zv11yv11θvy11θvx11θvz11zv12yv12θvx12zv22θvy12yv22θvx22}

(1)

式中：zv11,yv11,θvy11,θvx11和θvz11分别为车体的竖向位移、横向位移、俯仰角、转动角和平摆角；zv12,yv12和θvx12分别为车体前轴的竖向位移、横向位移和转动角；zv22,θvy12,yv22和θvx22分别为车辆后轴的竖向位移、俯仰角、横向位移和转动角。

图1 具有12个自由度的卡车模型示意图

1.2 桥梁模型

本文采用秦皇岛-大连跨海通道的非通航孔桥梁设计方案为研究对象，该桥梁设计方案为典型的高桩承台群桩基础结构型式，如图2(a)所示。图2(a)中MWL为平均海平面。桥梁上部结构采用5×120 m一联的连续钢箱梁，主梁顶面宽度为33.5 m，设置双向6车道，如图2(b)所示。桥梁下部结构采用钢管打入桩基础，钢筋混凝土桥墩为圆端空心墩，平面尺寸为3.5 m×10.0 m，壁厚为0.8 m。钢筋混凝土承台的平面尺寸为13.0 m×21.0 m×6.0 m，承台底部与13根直径为2.0 m的钢管打入桩连接。

为了充分考虑上部结构跨度之间的偶联效应，建立跨度为1 800 m的三联连续梁桥进行分析。将主梁建模为空间板单元，桥墩、承台以及钢管打入桩基础采用三维梁单元。动水压力通过附加水质量进行考虑，并施加在相应的水下桩柱节点位置。采用p-y曲线、t-z曲线和Q-z曲线计算土体对桩的横向、竖向和基底非线性约束刚度。利用瑞利阻尼对桥梁结构进行建模，瑞利阻尼系数对应于前两阶桥梁振型下的1%阻尼比。

需要说明，由于桥梁设计水位在承台底面处，冰荷载将直接作用于大尺度承台上。冰荷载的作用方式为各承台一致激励。上述所有模型全部集成于ABAQUS软件数值模拟平台，并借助二次开发进行研究。

(a) 桥梁立面图

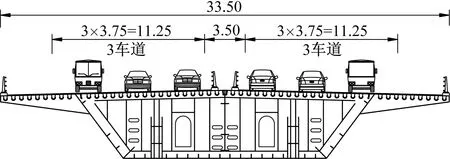
(b) 主梁截面

1.3 接触模型

在接触问题的研究中，罚函数法是一种解决约束优化问题行之有效的方法[12]。接触问题的约束方程可以表示为

(2)

式中：W(x)为目标函数；gi(x)为约束条件为x的函数。为了使目标函数W(x)最小，引入罚函数使得约束优化转化为无约束优化，转化后的约束方程可以表示为

(3)

式中：G[gi(x)]为罚函数；rk为罚函数的参数；m为约束条件数。

结构方程组由虚功原理导出，而虚功原理又由最小势能原理导出。实践证明，罚函数法可以转化为最小势能原理[13]。因此，如果以势能为目标函数，以接触情况为约束条件，如式(3)所示，罚函数方法是适用于接触问题的。

(4)

式中：Πp为整个系统的势能；gi(u)为接触面积上的间隙函数，它是接触点之间距离u的函数。

罚函数法在有限单元中的应用思想是在接触体之间增设虚拟弹簧，允许接触对象之间的虚拟假设。实际上，gi(u)在数值上可以是正的，也可以是负的，相应的正负值分别代表分离和接触机制。将虚弹性势能项引入式(4)中，势能函数的一般原理可以改写为

(5)

式中：Πp(u)为系统的势能；G[gi(u)]为罚函数。

研究结果表明[14]，无论是在静力分析还是动力分析情况下，对于分离、滑动及摩擦等接触问题，应用罚函数方法开展的数值计算都能得到比较精确的结果。因此，本研究利用罚函数定义了车轮与桥面之间的接触关系，将车轮与桥面的相互作用设置成硬接触，从而允许两者发生分离。

1.4 路面粗糙度

路面粗糙度是近似的高斯平稳随机过程[15]，为了简化对路面粗糙度的描述，国际标准ISO-8608[16]给出了模拟路面粗糙度的简化功率谱密度函数，可以表示为

(6)

式中：η为空间频率；η0为0.1cycle/m的参考频率；φ(η0)为粗糙度系数，m3/cycle，其值取决于路面状况。

假定路面粗糙度是一个零均值的平稳高斯随机过程。因此，路面粗糙度函数r(x)可以通过傅里叶逆变换得到，可以表示为

(7)

式中：θk为相位角，在0～2π变化；n为波数，cycle/m;N为模拟的点数;φ(nk)为路面粗糙度的功率谱密度函数;nk为第k点的波数，cycle/m。

本文根据国际标准ISO-8608中的规定，模拟了粗糙度系数为φ(n0)=20×10-6m3/cycle的等级“良好”的路面粗糙度平稳高斯随机过程，如图3所示。

图3 路面粗糙度随机过程

1.5 自激冰力模型

为了实现数值计算，通常将冰体挤压强度与应力速率表达式分段线性化，如图4所示。线性化后，冰体挤压强度与应力速率的多线性关系可近似为

(8)

图4 冰体挤压强度与应力速率的多线性关系

Määttänen[17]给出了冰体发生挤压破碎过程中的应力速率与相对速度的表达式

(9)

式中：D为结构直径；σc为冰体最大挤压强度；Vr为冰与结构相对速度。

对圆形承台截面的局部冰应力在-π/2～π/2内进行积分来获得结构整体冰力，如图5所示。局部冰应力还应包括径向正应力分量和切向剪应力分量。结构总冰力可表示为

(10)

联立式(8)和式(9)，结构总冰力可以改写为

(11)

式中，Vice为冰速。

图5 圆形结构上的冰应力分布示意图

其中，仅与冰速有关的冰力部分，可表示为

(12)

结构体系中新的阻尼系数可以表示为

(13)

式中，C为结构原始阻尼。

对于线性化模型，可按冰体应力速率分为3个分段函数进行冰力模拟，可以写为

(14)

阻尼系数随着冰体应力速率而变化，其分段表达式可以写为

(15)

1.6 冰-车-桥系统耦合动力方程

考虑水下桥梁桩基础的动水压力以及桩-土之间的相互作用，建立了包括附加水质量和非线性土弹簧的冰-车-桥系统的耦合动力方程，可以表示为

(16)

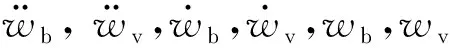
外力项Fbb包括两部分：① 车体重力，其大小保持不变，但随着车辆的移动其加载位置不断变化；② 车-桥相互作用力，包括车辆悬挂系统的弹簧力和阻尼力，取决于车辆和桥梁的动力响应。因此，相互作用力总是随着车辆移动而时变。同样，外力项Fvv由车-桥相互作用力产生，Fice为只与冰速相关的冰力项。

2 冰-车-桥系统耦合振动分析

2.1 工况设置

基于国际重型卡车速度限制的要求[18]，标准卡车行驶速度一般为70 km/h。此外，选取40 km/h和100 km/h的车辆速度作为车辆行驶中的低速和高速进行对比分析。在实际道路交通中，不同驾驶员保持的车头时距会有显著差别，同一个驾驶员保持的车头时距也会随着个人状态和环境影响而发生变化。本文采用的车头间距按照国际上规定的两秒定律[19]，两辆相邻车辆之间的最小安全间距由车速乘以2 s来估计，即：最短车头时距取2 s左右的行程。为了满足安全行车条件下的最小安全间距，将不同车速工况下的行车距离设置为55 m (2 s×100 km/h)，39 m (2 s×70km/h)，22 m (2 s×40 km/h)的均匀间距。为了模拟真实的车流情况，本研究假设共有18辆车在桥梁左幅的3条车道上行驶，每条车道上等间距的设置6辆车作为考虑的车辆流进行分析。

采用全桥模型的中跨跨中点作为桥梁结构反应测点进行桥梁振动分析，将车流中的第一辆车(头车)作为目标车辆进行车辆振动及行车安全研究。本文还考虑了不同冰速的影响。冰速选取vi1= 0.6 m/s，vi2= 0.8 m/s和vi3= 1.0 m/s作为慢、中、快冰速进行对比分析。冰厚取为0.46 m(五十年一遇设计单层冰冰厚)，海冰挤压强度取为2.15 MPa(五十年一遇设计海冰强度)[20]。

2.2 桥梁振动分析

车辆以3种不同的行驶速度通过桥梁时，在冰速为1.0 m/s的情况下桥梁跨中测点的竖向位移反应情况，如图6所示。为了便于观察，横坐标设置为vvt/L。其中：vv为车速；t为车辆行驶时间；L为桥梁跨度。由图6可知，随着车辆行驶速度的增加，桥梁竖向位移反应具有增大的趋势。例如，车辆行驶速度为100 km/h的桥梁最大竖向位移比行驶速度为40 km/h的增加了20%。这是因为桥梁的竖向位移反应主要是由车体自质量所引起的，由于桥面粗糙度的作用，车辆行驶速度越快，车-桥相互作用力越大，从而引起了更大的桥梁竖向位移。当车辆以100 km/h的行驶速度通过桥梁时，在3种不同冰速的情况下桥梁跨中测点的竖向位移反应情况，如图7所示。由图7可知，冰荷载的作用对于桥梁的竖向位移反应影响很小，这是因为冰荷载的作用方向是沿着桥梁横向施加的，这与不考虑动冰荷载作用下的车-桥耦合振动研究结果相似[21]。

当车辆以100 km/h的行驶速度通过桥梁时，3种不同冰速情况下桥梁跨中测点的横向位移反应情况，如图8所示。由图8可知，桥梁的横向位移反应明显受到了不同冰速的影响。随着冰速的增大，桥梁的横向位移反应具有明显增大的趋势。例如，当冰速从0.6 m/s增加到1.0 m/s时，桥梁的最大横向位移从0.104 m增加到0.211 m，相比增长125%。这说明快冰速会增大冰与桥梁结构的相互作用力，进而引起更大的桥梁振动。当车辆以3种不同的行驶速度通过桥梁时，在冰速为1.0 m/s的情况下桥梁跨中测点的横向位移反应情况，如图9所示。由图9可知，车速的变化对于桥梁的横向位移反应影响不大，这是由于车辆在行驶过程中车体的振动只在竖向上影响桥梁，对于桥梁的横向动力反应贡献很小。

2.3 车辆振动分析

当车辆以3种不同的行驶速度通过桥梁时，在冰速为1.0 m/s的情况下车辆的竖向加速度反应情况，如图10所示。由图10可知，随着车速的增加，车辆的竖向加速度反应具有明显增大的趋势。例如，当车速为40 km/h，70 km/h和100 km/h时，车辆的最大竖向加速度分别为0.84 m/s2，1.08 m/s2和1.89 m/s2。这是因为由于路面粗糙度的作用，车辆在高速行驶的过程中产生了更大的车-桥相互作用力，进而引起了更大的车辆竖向振动。此外，由2.2节可知，不同冰速仅对桥梁的竖向位移产生了轻微的影响。可以预见，冰速的变化对车体竖向振动反应影响不大，故本节不再赘述。

当车辆以100 km/h的行驶速度通过桥梁时，3种不同冰速情况下车辆的横向加速度反应情况，如图11所示。由图11可知，随着冰速的增加，车辆的横向加速度反应呈现明显增大的趋势。例如，当冰速从0.6 m/s增加到1.0 m/s时，车体的最大横向加速度从0.817 m/s2增加到2.283 m/s2，相比增长179%。这是因为随着冰速的增大，桥梁的横向振动反应增加，进而通过车-桥耦合作用力传递给桥上行驶的车辆。另外，由2.2节分析可知，不同车速对于桥梁的横向动力反应影响不大。可以预见，车速的变化对车体横向振动影响轻微，故本节不再赘述。综上所述，车辆的竖向振动反应受车速的影响较为明显，随车速的增加而增大；车辆的横向振动反应随冰速的增加而增大，受到了冰荷载的控制。

3 行车安全分析

3.1 车辆侧滑评价指标

本文给出了桥上车辆行驶过程中的侧滑评价指标，车辆某一车轴的侧滑抗力FSR可以表示为

FSR=μFz,left+Fz,right-Fx,left+Fx,right

(17)

式中：Fz,left和Fz,right分别为某一车轴的左轮和右轮的竖向接触力；Fx,left和Fx,right分别为某一车轴的左轮和右轮的横向接触力；μ为车轮与桥面的摩擦因数，本文选取摩擦因数μ= 0.6[22]。由式(17)可知，当车辆的侧滑抗力接近0时，说明车辆接近于侧滑状态。

3.2 冰速的影响

当车辆以100 km/h的行驶速度通过桥梁时，3种不同冰速情况下车辆前轴和后轴的竖向接触力，如图12所示。由图12可知，冰速的变化对车辆的竖向接触力影响不大，这是由于冰速只会影响冰与桥梁结构的横向相互作用力，而车辆的竖向振动主要是受到了桥面粗糙度的影响。因此，当车辆以同一速度在桥上行驶时车辆的竖向接触力几乎保持不变。当车辆以100 km/h的行驶速度通过桥梁时，3种不同冰速情况下车辆前轴和后轴的横向接触力，如图13所示。由图13可知，随着冰速的增加，车辆前、后轴的横向接触力明显增大，这说明快冰速增大了冰与桥梁结构的相互作用力，同时增大了桥梁传递给车辆的横向接触力。

(a) 前轴竖向接触力

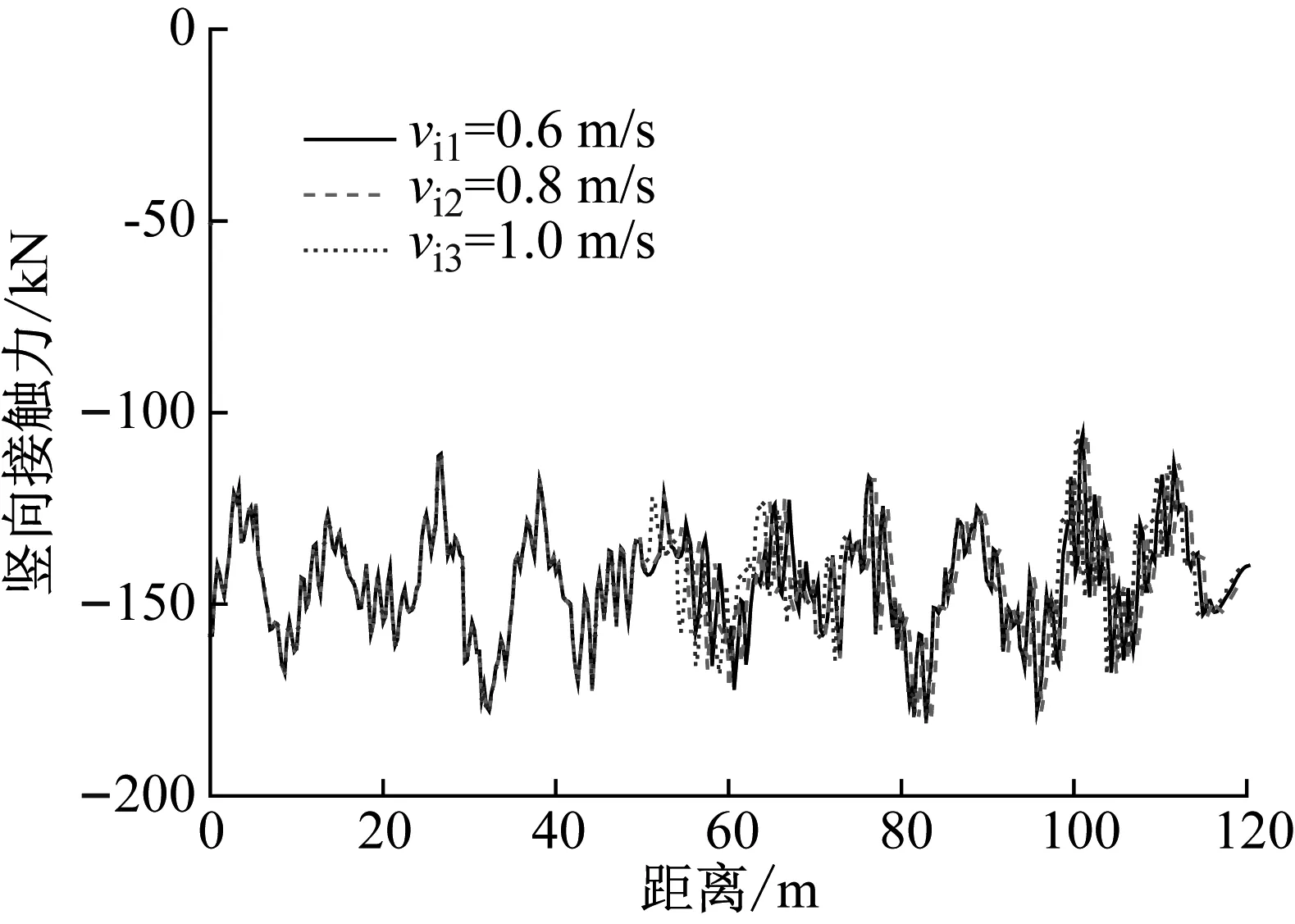
(b) 后轴竖向接触力

当车辆以100 km/h的行驶速度通过桥梁时，3种不同冰速情况下车辆前轴和后轴的最小侧滑抗力，如图14所示。由图14可知，随着冰速的增大，车辆的最小侧滑抗力明显减小。当冰速为0.6 m/s和0.8 m/s时，前轴的最小侧滑抗力为17.62 kN和15.16 kN。然而，当冰速为1.0 m/s时，前轴的最小侧滑抗力仅为12.56 kN。结果表明，冰速的增大会降低抵抗侧滑的安全储备力，对桥上车辆的行驶安全不利。此外，车辆前轴车轮的最小侧滑抗力要低于后轴车轮的最小侧滑抗力。例如，在冰速为1.0 m/s时，前轴的最小侧滑抗力为12.56 kN，后轴的最小侧滑抗力为40.41 kN。这说明冰荷载作用下桥上车辆的前轴车轮比后轴车轮更容易发生侧滑。

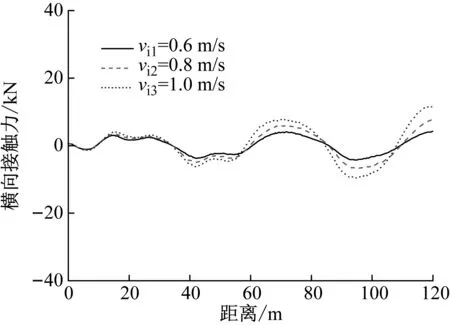
(a) 前轴横向接触力

(b) 后轴横向接触力

3.3 车速的影响

当车辆以3种不同的行驶速度通过桥梁时，在冰速为1.0 m/s的情况下车辆前轴和后轴的竖向接触力，如图15所示。由图15可知，随着车速的增加，车辆前、后轴的竖向接触力明显增大，这说明了车辆在同样的粗糙度桥面上行驶时，车速对车辆的竖向接触力具有显著影响。由图15还可知，后轴的竖向接触力远大于前轴的竖向接触力，这是由于车体重心位于整体车身的后部所导致的。

当车辆以3种不同的行驶速度通过桥梁时，在冰速为1.0 m/s的情况下车辆前轴和后轴的横向接触力和最小侧滑抗力，分别如图16、图17所示。由图16和17可知，无论前轴或后轴，车辆的横向接触力和最小侧滑抗力均随着车速的增大而减小。这是由于冰激桥梁结构自激振动会随着冰与结构的相互作用时间的增加而增大，最终稳定在固定的振幅上。当车速较慢时车辆的过桥时间较长，增加了冰与桥梁结构相互作用的时长。因此，以较慢车速行驶的车辆会受到更大的振动反应，从而使得车辆的横向接触力增大，侧滑抗力减小。例如，当车速为100 km/h和70 km/h时，前轴的最小侧滑抗力为13.31 kN和11.56 kN。然而，当车速为40 km/h时，前轴的最小侧滑抗力仅为8.84 kN。

(a) 前轴最小侧滑抗力

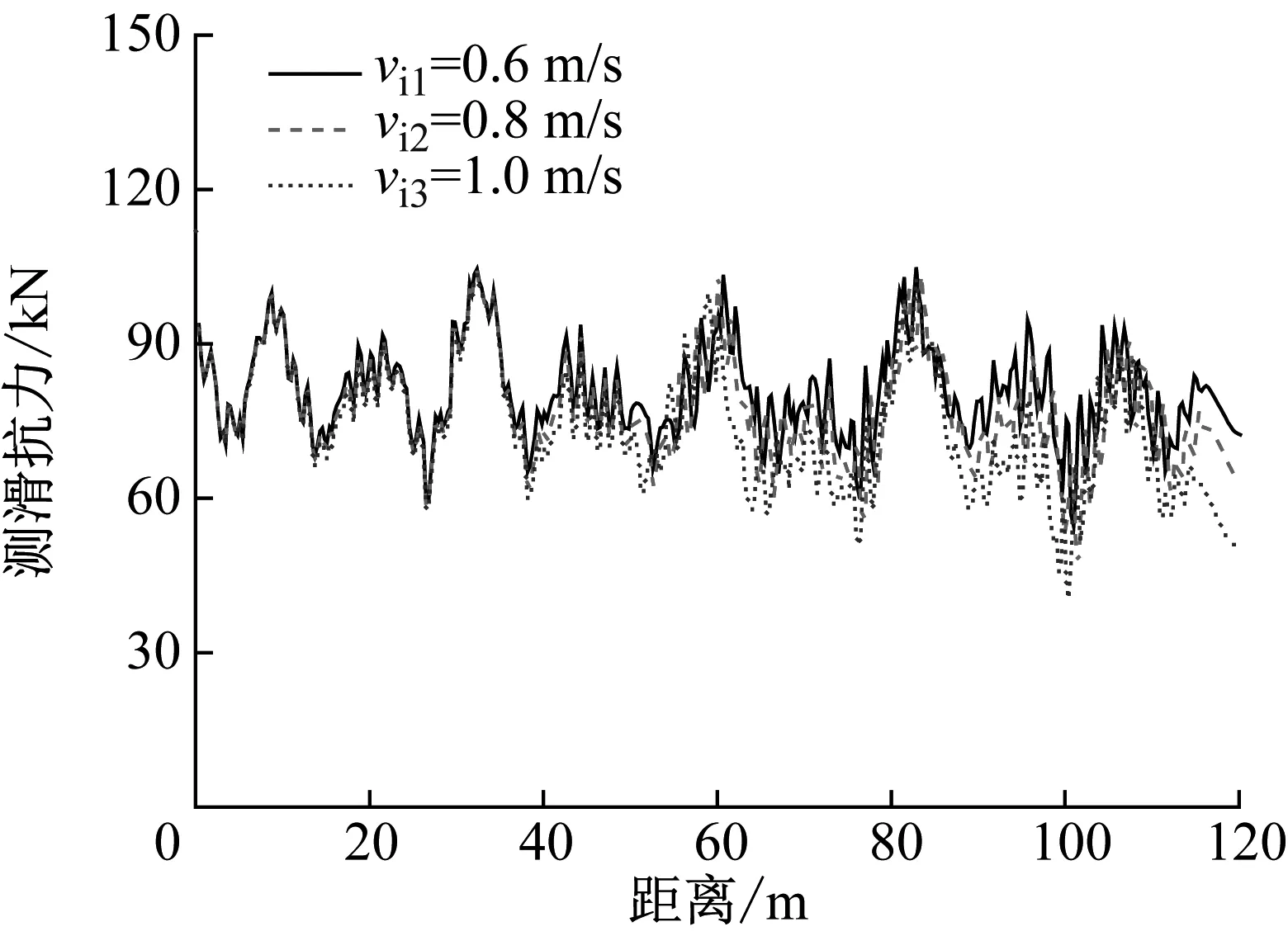
(b) 后轴最小侧滑抗力

(a) 前轴竖向接触力

(b) 后轴竖向接触力

由图17还可知，车辆前轴的侧滑抗力远低于后轴的侧滑抗力。例如，在车速为40 km/h时，前轴的最小侧滑抗力为8.84 kN，后轴的最小侧滑抗力为25.82 kN。此时，车辆的后轴车轮处在较为安全的状态，然而车辆的前轴车轮非常接近侧滑状态，只有约为8 kN的安全储备。

(a) 前轴横向接触力

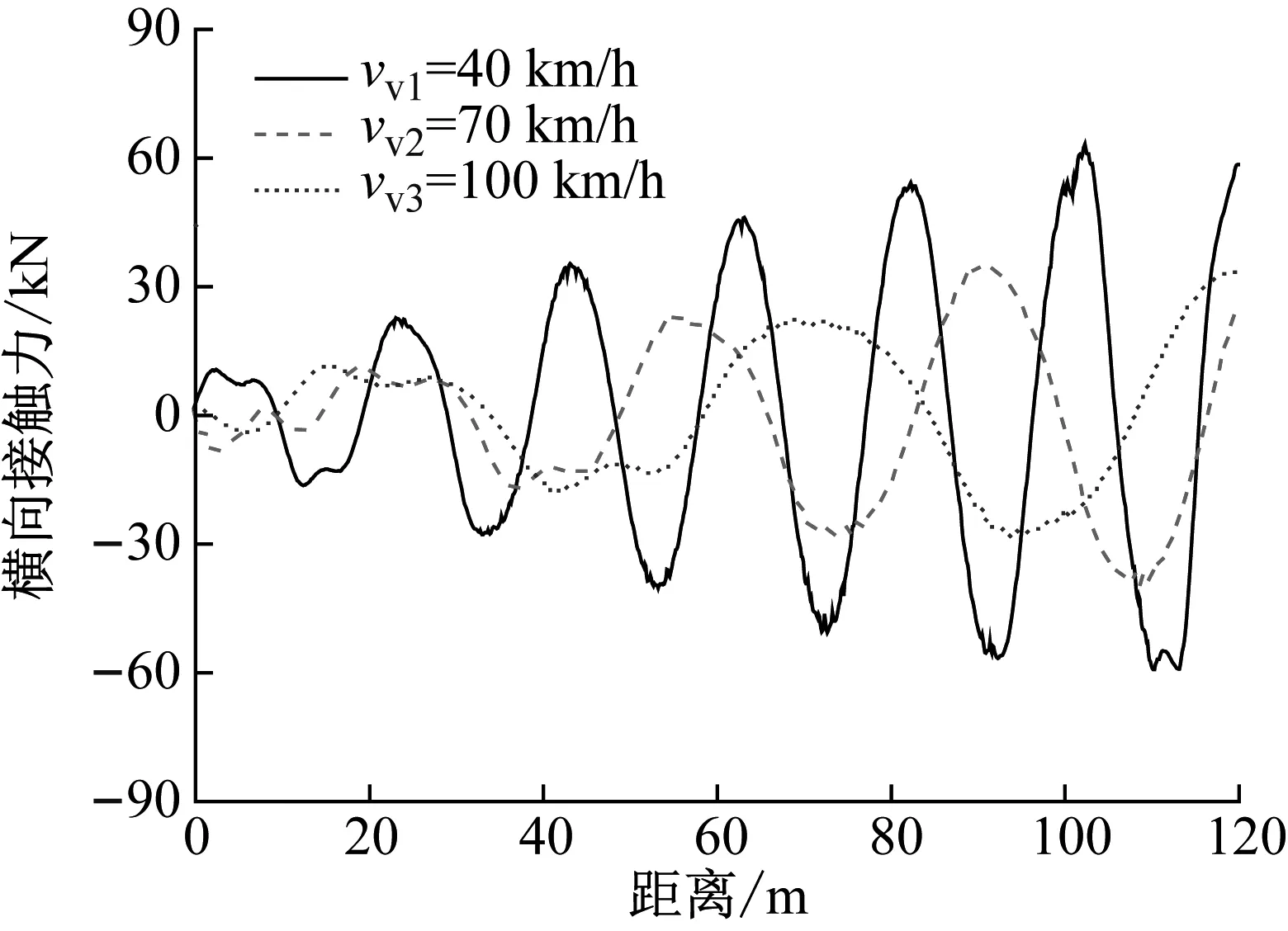
(b) 后轴横向接触力

(a) 前轴最小侧滑抗力

(b) 后轴最小侧滑抗力

4 结 论

(1) 随着车辆行驶速度的增加，桥梁和车辆的竖向动力反应均明显增大。车辆行驶速度为100 km/h的桥梁最大竖向位移和车辆最大竖向加速度分别比40 km/h时增加了20%和125%；随着冰速的增加，冰与车-桥系统的相互作用力增大，桥梁和车辆的横向动力反应均明显增大。当冰速从0.6 m/s增加到1.0 m/s时，桥梁的最大横向位移和车辆的最大横向加速度分别增加了102%和179%。这说明了车辆与桥梁的交互作用受到了车速和冰速的双重影响。

(2) 当冰速从0.6 m/s增加到1.0 m/s时，车辆前、后轴的横向接触力均呈现增大趋势，车辆前轴的最小侧滑抗力从17.62 kN降低到12.56 kN。这说明快冰速会增大车辆的横向接触力，降低车辆的最小侧滑抗力，不利于行车安全。此外，研究还发现桥上车辆的前轴车轮比后轴车轮更容易发生侧滑。

(3) 车辆的横向接触力和最小侧滑抗力均随着车速的增大而减小。这是由于冰激桥梁自激振动会随着冰与结构的相互作用时间的增加而增大，最终稳定在固定的振幅上。当车速较慢时车辆的过桥时间较长，增加了冰与桥梁结构相互作用时长。因此，以较慢车速行驶的车辆会受到更大的振动反应，从而使得车辆的横向接触力增大，侧滑抗力减小，对行车安全不利。

(4) 本文所提出的车-桥-冰系统耦合分析框架可为冰荷载作用下跨海桥梁行车安全评估提供参考。