基于改进自适应经验傅里叶分解的滚动轴承故障诊断方法

曹仕骏， 郑近德， 潘海洋， 童靳于， 刘庆运

(1.特种重载机器人安徽省重点实验室，安徽 马鞍山 243032；2.安徽工业大学 机械工程学院，安徽 马鞍山 243032)

滚动轴承是旋转机械设备中的重要组成部分，是工业领域中应用最为广泛、但同时也是最容易出现故障的旋转机械零部件之一。机械设备中有将近21%的故障是由滚动轴承故障引起的[1]，滚动轴承的运行状态是否正常直接影响整个机器的运行状态和性能[2]。因此，开展滚动轴承故障诊断方法的研究具有重要的现实意义。

具有局部故障的滚动轴承的信号往往是非平稳的，传统的傅里叶变换只能处理线性和平稳信号，时频分析可以同时获得时域特征和频域特征上的信息[3-4]，能够分析非平稳信号的局部化特征，被广泛应用于滚动轴承故障诊断[5]。常见的时频分析方法有小波分析[6]，Wigner-Ville分布[7]，短时傅里叶变换[8]等，然而这些时频分析方法都有各自不同的特点和局限[9]，其中一个共同缺陷是缺乏自适应性。

经验模态分解(empirical mode decomposition，EMD)[10-11]是Huang等[12-13]在1998年提出的一种数据驱动的非平稳信号处理方法，该方法无须预先设定任何基函数，依靠时间尺度特征来进行信号分解，在很多领域得到了广泛的应用。但EMD方法也存在不足之处，如模态混叠，过包络，欠包络和端点效应等，且算法本身缺少完整的理论基础。针对此问题，程军圣等[14]提出了一种新的自适应分解方法——局部特征尺度分解(local characteristic-scale decomposition，LCD)方法，该方法是对局部均值点采用三次样条方法得到均值曲线，与EMD方法相比，可以克服过包络和欠包络，抑制端点效应，计算时间等有一定的优势[14-16]，但仍然不可避免地出现端点效应和模态混叠。Gilles等[17-18]提出了经验小波变换(empirical wavelet transform，EWT)，该方法是在小波变换的基础上提出来的，具有较快的计算速度和完备的理论基础[17]。该方法通过先预设分解的模态个数N，再对原始信号的频谱进行自适应分割，得到N个区间，然后对每个区间通过尺度函数和小波函数构造正交小波滤波器组来进行重构，从而得到单分量信号。EWT方法在受噪声影响和频率成分比较复杂时，频谱分割的效果比较差，从而影响EWT方法的分解效果。EWT方法关键问题是傅里叶频谱分割，众多学者对EWT方法进行了改进，李从志[19]提出了基于频谱包络的改进EWT方法，郑近德等[20]提出了自适应经验傅里叶分解(adaptive empirical Fourier decomposition，AEFD)，该方法能将一个非平稳信号自适应地分解为若干个瞬时频率具有物理意义的单分量信号之和，但是AEFD方法分割的边界集需要人为经验设置，不具有自适应性。

为了克服AEFD方法的缺陷，受改进EWT方法启发，论文提出了改进的自适应经验傅里叶分解(enhanced adaptive empirical Fourier decomposition，EAEFD)，EAEFD方法以快速傅里叶变换为基础，再以包络熵值[21]最小作为评价指标得到最优的分解模态数N，其次采用频谱极大值包络的频谱分割技术得到分割边界和边界集，最后对每个边界集进行逆快速傅里叶变换，从而得到若干个瞬时频率具有物理意义的单分量信号。最后，通过仿真信号和具有局部故障的滚动轴承振动信号分析，将所提出的EAEFD方法分别与EWT，EMD和LCD等方法进行了对比，试验结果表明：EAEFD方法不仅能够有效诊断滚动轴承的局部故障，而且诊断精度比所对比的方法更高。

1 改进的自适应经验傅里叶分解方法

论文提出的EAEFD方法包括两个部分：一是对傅里叶频谱进行自适应分割，得到合理的分割边界；二是对傅里叶频谱分割得到的区间采用逆快速傅里叶变换进行重构。EAEFD方法能够将一个非线性非平稳的信号自适应的分解为若干个瞬时频率具有物理意义的傅里叶本征模态函数(Fourier intrinsic mode function, FIMF)之和，且该分解方法具有自适应性、完备性、局部性和正交性。

为了自适应分割傅里叶频谱，选取分解最优的模态数N，论文采用包络谱熵作为EAEFD方法分解效果的评价指标。将EAEFD方法分解得到FIMF分量信号通过Hilbert解调运算后得到的包络信号处理成一个概率分布序列pj，由此得到的熵值称为包络熵值，包络熵值可以反应原始信号的稀疏特性。得到的包络熵值越大，则分量信号的稀疏性越弱，反之包络熵值越小，则分量信号的稀疏性越强，波形中出现规律性冲击脉冲越明显。信号x(j)(j=1,2,…,K)的包络熵Ep可以表示为

(1)

式中：a(j)为信号x(j)经过Hilbert解调运算后得到的包络信号；pj为a(j)归一化形式，即概率分布序列。

EAEFD方法步骤具体如下：

步骤1对原始信号x(t)进行快速傅里叶变换(fast Fourier transform,FFT)，得到其复系数F(ω)，再计算傅里叶频谱，原始信号x(t)的傅里叶变换为

(2)

记原始信号x(t)的傅里叶频谱为f(ω)=F(ω)。

步骤2对傅里叶频谱f(ω)进行自适应分割，确定分解的模态个数N，设置分解模态数初始为N=2和搜索范围，执行步骤4～步骤9。

步骤3计算模态数目为N的各FIMF分量的包络谱熵值，则可以确定此N下的最小包络谱熵值，称之为局部极小熵值，再比较搜索范围内中各模态数的包络谱熵值，从而确定搜索范围内的最小包络熵值，最后确定分解方法中最优模态数目N。

步骤4找出并记录频谱中所有的Emax个极大值和Emin个极小值的位置。

步骤5如果Emin>5N，则进入步骤6，反之Emin≤5N，则进入步骤7。由于在步骤6中，每当频谱包络检测处理一次，Emin个极小值以1/3左右的倍率衰减，将Emin与模态个数N设置为5倍的关系是为了保证最后一次频谱包络检测处理的极小值个数大于所需要分解的模态个数N。

步骤6连接所有的极大值，得到极大值包络曲线，再统计包络曲线的极小值和极大值的个数并记录其位置，此时的极小值个数记为Emin，极大值个数记为Emax，则返回步骤5。

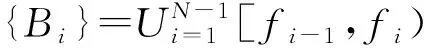
(3)

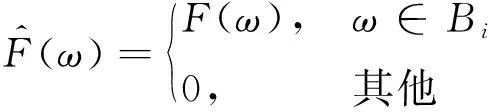
(4)

步骤9最后得到每个区间Bi重构的FIMF分量，记为

xi(t)=ρi(t)eφi(t),i=1,2，…，N

(5)

则原始信号可以表示为

(6)

EAEFD方法以快速傅里叶变换为基础，以包络熵值最小作为评价指标，确定最优分解模态数目，再采用极大值包络方法自适应地获得一个合理的分割边界，最后再采用逆快速傅里叶变换对每个区间进行重构得到FIMF分量。故该方法能将一个复杂的信号自适应地分解为若干个瞬时频率具有物理意义单分量信号(FIMF)之和。该方法将经典的常幅值和常频率的傅里叶展开扩展成为变幅值和变频率的广义傅里叶展开。由于EAEFD方法是自适应地将整个频谱分成若干个区间，再分别对每个区间进行重构，该分解方法具有自适应性、完备性、局部性和正交性。

EAEFD方法具体流程如图1所示。

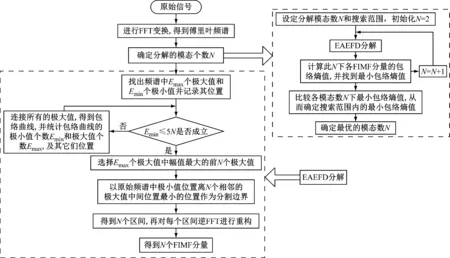
图1 EAEFD方法流程图

2 仿真信号对比分析

为了验证论文所提方法的有效性，采用式(7)所示的仿真信号x(t)进行分析

x(t)=x1(t)+x2(t)+x3(t)

(7)

式中:x1(t)=1.5e-0.5tcos(30πt+6πt2);x2(t)=0.5sin(90πt);采样频率为Fs=1 024 Hz；x3(t)=(0.5+0.6sin(6πt))sin(140πt+1.5cos(6πt))；x(t)是由两个调幅调频分量和一个正弦分量组成，x(t)和各个分量的时域波形图如图2所示。

首先，采用EAEFD方法对仿真信号x(t)分解，初始化模态数N=2，设定N的搜索范围为[2,8]，利用最小包络熵值原则优化模态数N，模态数N与局部极小熵值关系如图3所示。从图3可以看出，当N=3时，取得最小包络熵值为2.867 6，因此，最优模态数N=3，这也与仿真信号三个分量吻合。由于EAEFD方法最优的分解模态数N=3，此时频谱包络检测处理次数为0次。

(a)

(b)

(c)

(d)

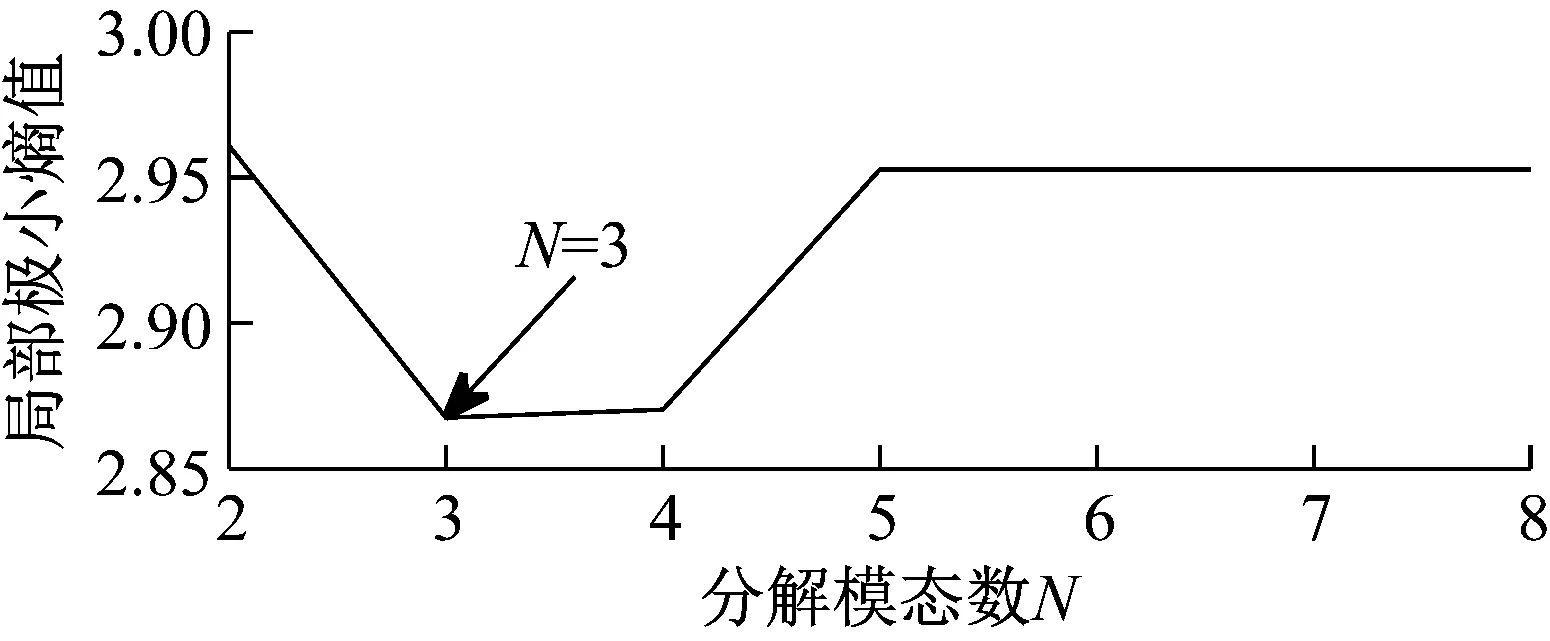
图3 局部极小熵值随分解模态数N的变化曲线

其次，为了比较EAEFD，EWT，EMD，LCD和AEFD方法分解的效果，分别采用这五种方法对x(t)进行分解，EWT方法在傅里叶频谱中取幅值最大的前N个极大值，将前N个极大值的中点位置作为分割边界，获得分割边界后再通过尺度函数和小波函数构造正交小波滤波器组来进行重构，AEFD方法初始边界集根据频谱设置为[19,63]，EMD和LCD方法终止判据是标准偏差法(standard deviation,SD)[22]，当SD<0.3时终止迭代，且LCD方法中参数a=0.5,由于EMD分解得到的分量比较多，从第四个分量开始波形比较相似，故选取前四个分量，图4(a)和图4(b)分别为EAEFD和EWT的频谱的分割边界，由图4可知，EAEFD方法能够将原始信号的三个分量的傅里叶频谱划分开，得到合理的分割边界，而EWT方法未将三个分量的傅里叶频谱划分开，而是将原始信号中的第一个分量的频谱划分成两个区间，即对应EWT方法分解得到的前两个分量，并且将原始信号中的第二个分量和第三个分量划分至同一个区间，对应EWT方法分解得到的第三个分量，故EWT的分解效果不佳。EAEFD方法与EWT、EMD和LCD方法相比较，EAEFD方法分解效果是最优的。

(a) EAEFD

(b) EWT

分别采用五种方法对仿真信号x(t)进行分解，分解结果如图5(a)～图5(e)所示。由图5(b)可知，从时域波形上看，EWT分解得到的分量出现了模态混叠和端点效应(虚框所示)，分解得到的三个分量与对应真实分量相差较大；由图5(c)中虚框所示，EMD方法分解得到的第二个分量波形对应x1(t)，该分解方法得到的分量也同样存在模态混叠；由图5(d)可知，LCD方法分解得到的第一个分量对应x3(t)，第二个和第三个分量发生了严重模态混叠(虚框所示)；如图5(e)中虚框所示，AEFD方法的第二个分量存在严重的模态混叠，第三个分量波形对应真实分量，但幅值发生了变化，该方法未将仿真信号中的三个分量分开。EWT和EMD方法未将原始信号中第二个和第三个分量分离。由图5(a)可知，论文提出的EAEFD方法分解得到的三个分量分别对应仿真信号x(t)中的x1(t)，x2(t)，x3(t)，波形和原始信号的三个分量吻合，保真性比较好。

为了更加直观地对比五种方法分解得到的分量的精确性，论文给出了五种方法得到的分量与真实分量之间的绝对幅值误差，如图6所示。其中绝对幅值误差定义为分解得到的分量与真实分量之差的绝对值，由图6可知，与EWT，EMD，LCD和AEFD方法对比，论文提出的EAEFD方法分解得到的三个分量绝对幅值误差均是最小的，且绝对幅值误差趋近于零，故该方法分解得到的分量精确性是最高的，同时也说明了EAEFD方法分解效果具有一定的优势。

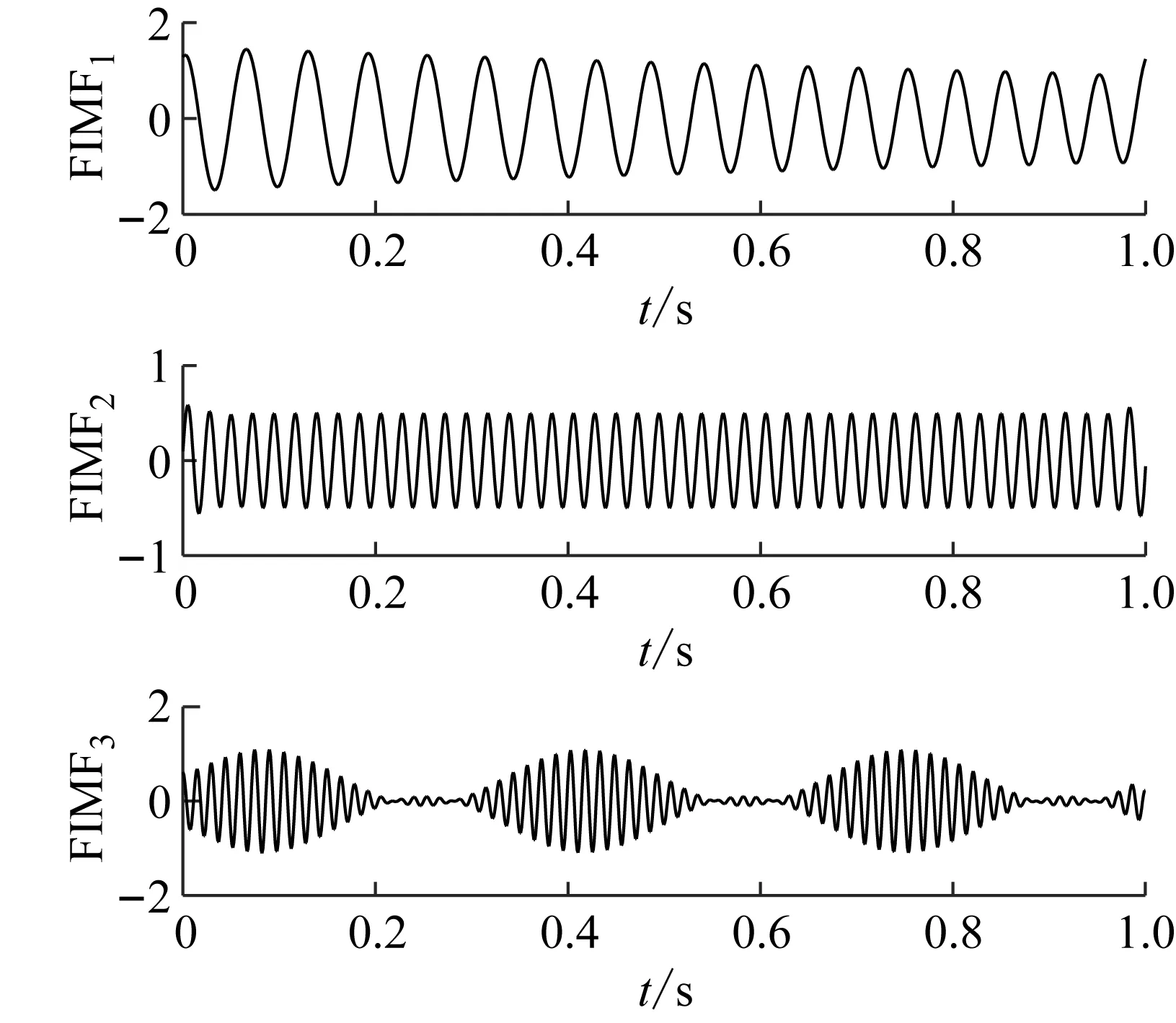
(a) EAEFD

(b) EWT

(c) EMD

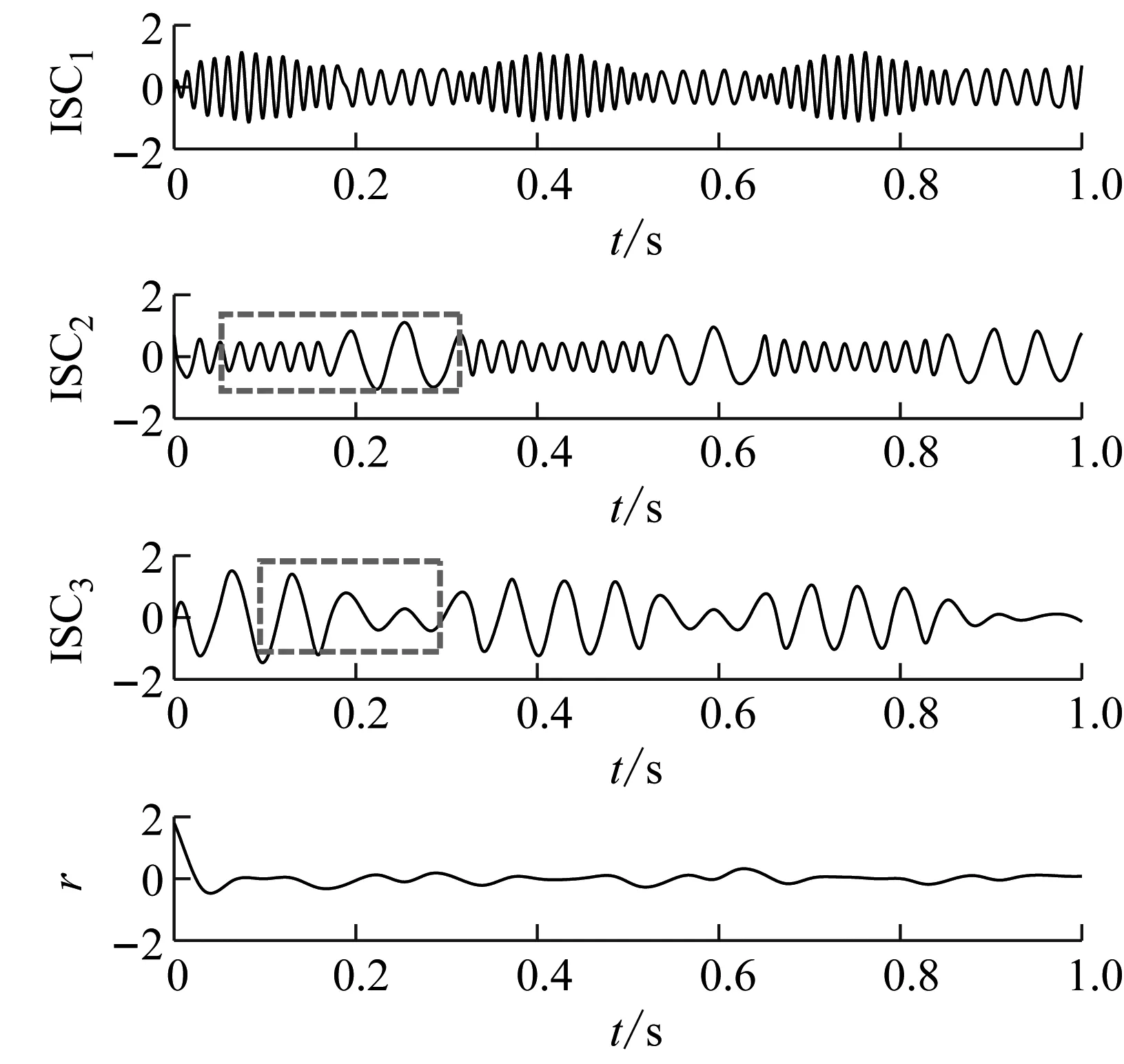
(d) LCD

(e) AEFD

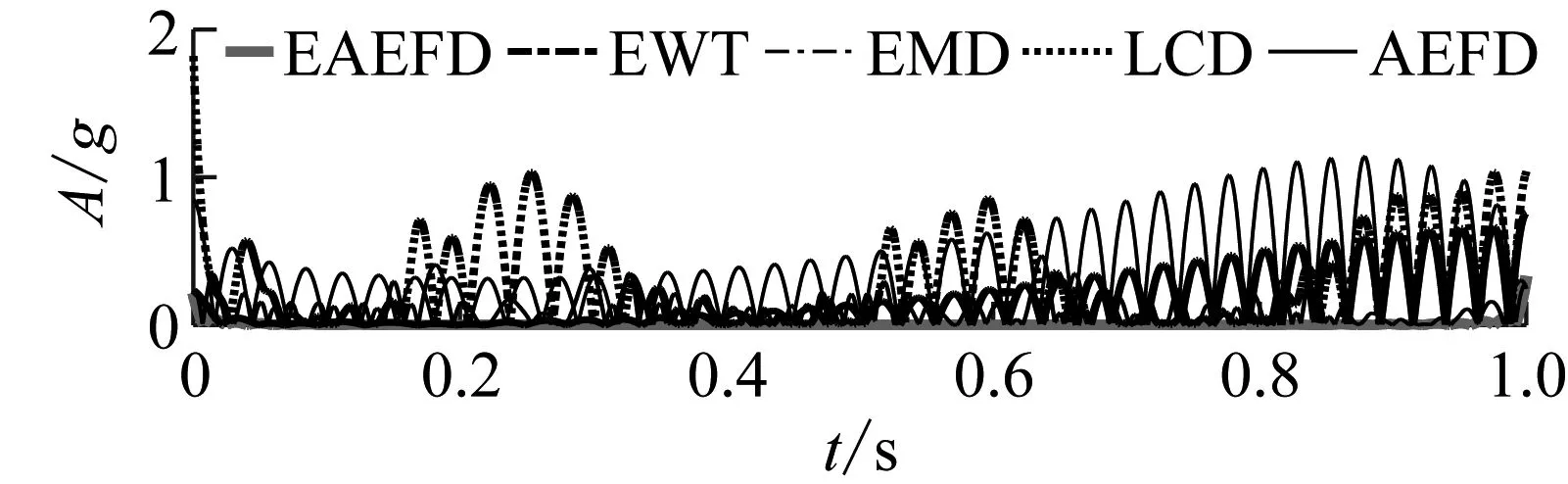
(a)

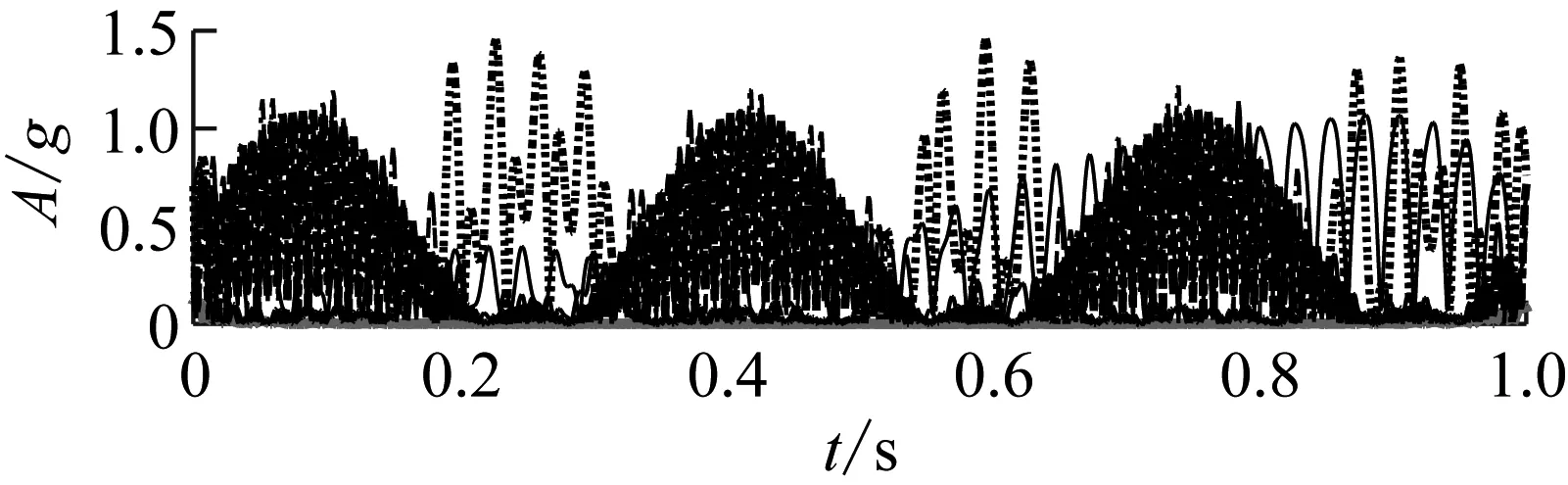
(b)

(c)

最后，为了进一步验证论文所提出方法的有效性，表1给出了五种分解方法分解得到的分量与真实分量之间的相关系数R，表2给出了五种分解方法的分解正交性指标(index of orthogonality，IO)和五种分解方法分解得到的分量与真实分量之间的误差能量比ER。相关系数越大，说明相关性越好，正交性指标越小，说明分解的正交性越好，误差能量比越小，说明误差越小。其中误差能量比(ER)，正交性指标(IO)和相关系数(R)分别定义为

(8)

(9)

(10)

式中：i,j=1,2,3;yi(t)和yj(t)为分解方法得到的第i个和第j个分量。

表1 五种分解方法的x(t)相关系数的评价指标对比

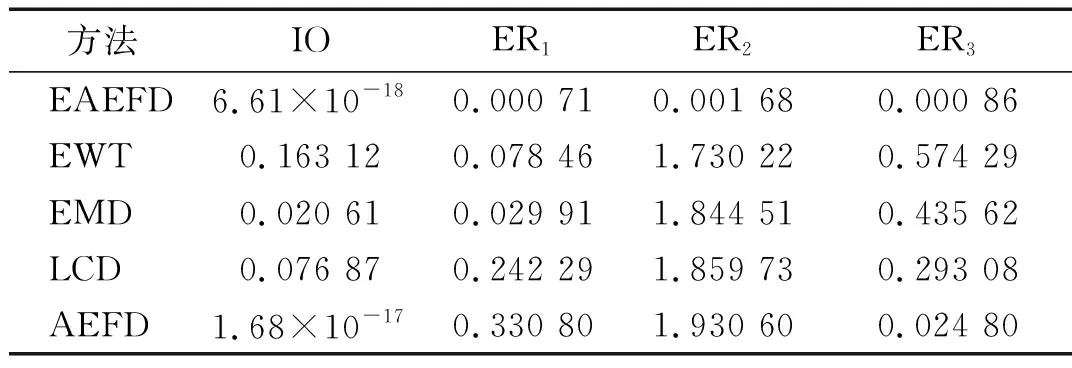
表2 五种分解方法的x(t)正交性和误差能量比的评价指标对比

由表1可知，在第一个分量中，EAEFD方法分解得到的分量相关系数是最高的，EMD和EWT方法分解得到分量相关系数比EAEFD方法分解得到的分量相关系数略小，AEFD和LCD方法分解得到的分量相关系数最小；在第二个分量中，EAEFD方法分解得到的分量相关系数同样是最高的，而其他四种方法分解得到的分量相关系数均较小，可以说明在分解过程中存在一定程度的模态混叠，没有将各个分量完全分开；在第三个分量中，EAEFD方法分解得到的分量相关系数仍然是最高的，AEFD方法分解得到的分量相关系数仅次之，EMD和LCD方法分解得到的分量相关系数再次之，EWT和EMD方法分解得到的分量相关系数最小，EAEFD方法分解得到的三个分量与原始信号的三个分量相关系数均达到0.99，相关性较大，也验证了论文所提方法的有效性。

由表2可知，EAEFD方法分解结果的正交性指标几乎为零，说明了各FIMF分量是相互独立的，AEFD方法分解结果的正交性指标比EAEFD方法分解结果的正交性指标略大，而EWT方法分解结果的正交性指标最大，EMD和LCD方法分解结果的正交性指标相比EWT方法分解结果的正交性指标略小一点，而正交性指标越小越能说明分解的正交性越好，故EAEFD方法的正交性是最好的。此外，从绝对误差能量比上来看，在第一个分量中，EAEFD方法得到的分量绝对误差能量比是最小的，EMD和EWT方法得到的分量绝对误差能量比则次之，LCD和AEFD方法得到的分量绝对误差能量比是最大的；在第二个分量中，EAEFD方法得到的分量绝对误差能量比也是最小的，其他的四种方法得到的分量绝对误差能量比均比较大；在第三个分量中，EAEFD方法得到的分量绝对误差能量比仍然是最小的，AEFD方法得到的分量绝对误差能量比则次之，LCD方法得到的分量绝对误差能量比再次之，EWT和EMD方法得到的分量绝对误差能量比是最大的。

综合以上分析，EAEFD方法与EWT，EMD，LCD和AEFD方法相比较，EAEFD方法分解得到的FIMF分量在相关性、正交性和精确性等方面均有一定的优越性。

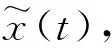
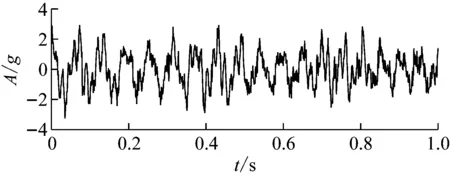
图7 含噪声的仿真信号时域波形

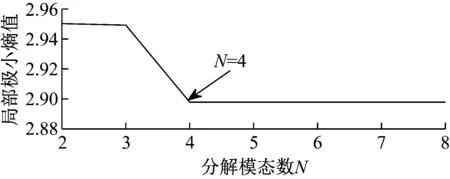
图8 局部极小熵值随分解模态数N的变化曲线

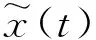
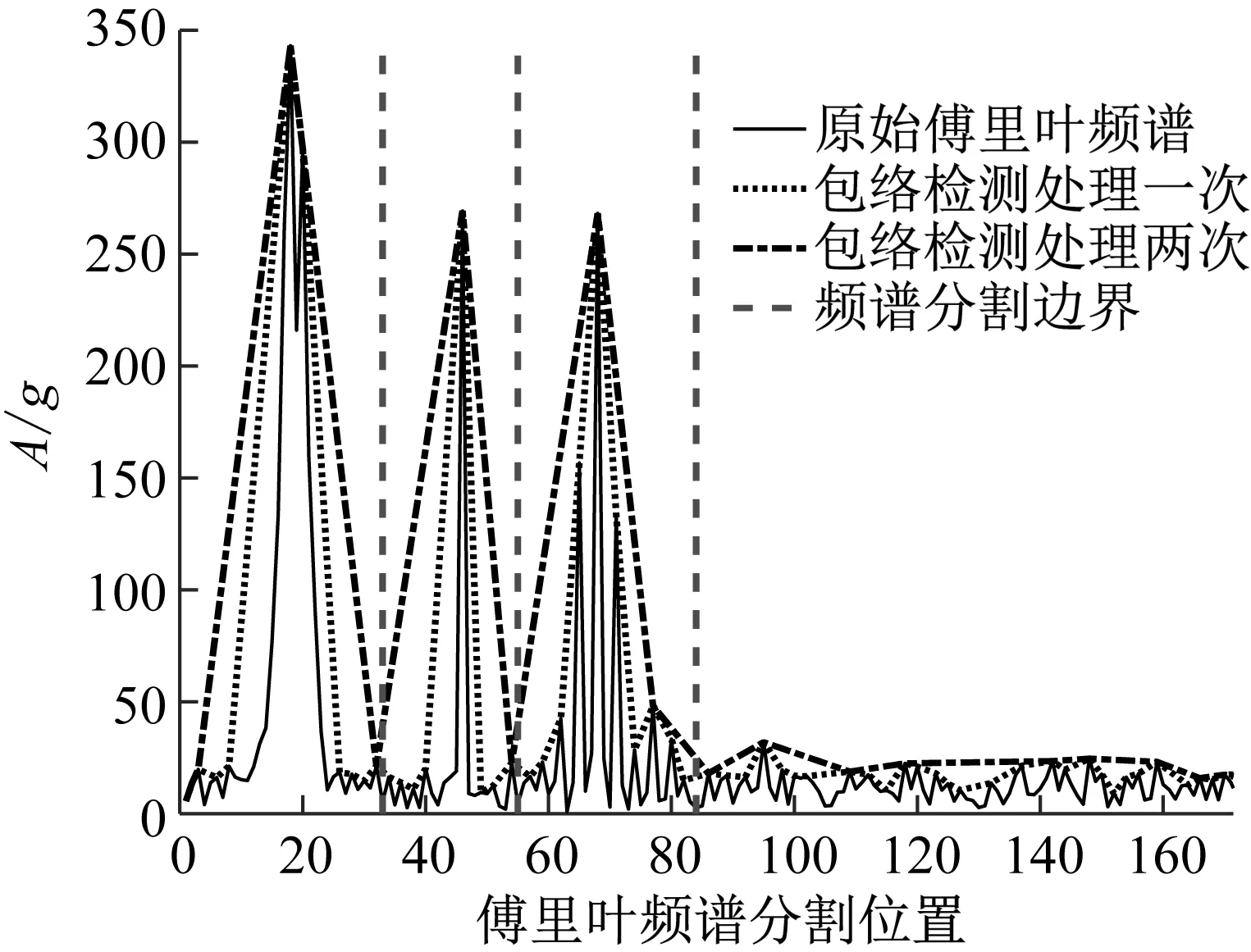
(a) EAEFD

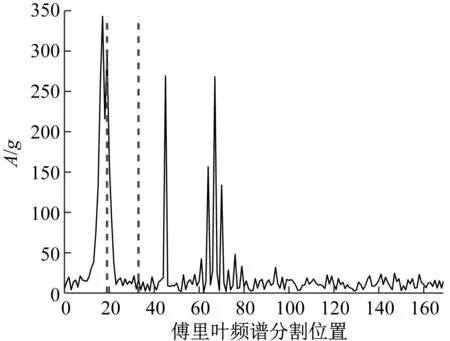
(b) EWT

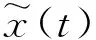
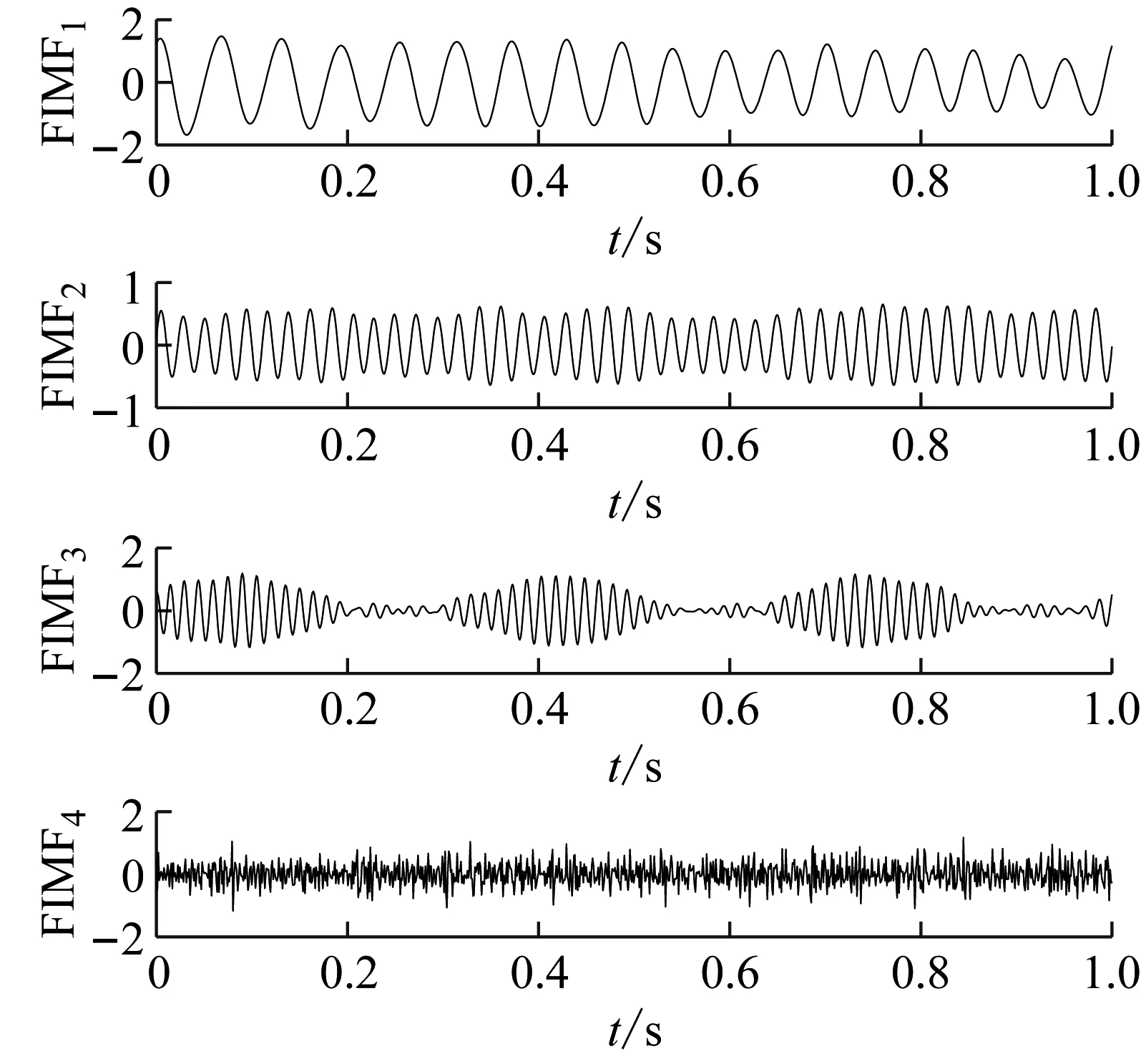
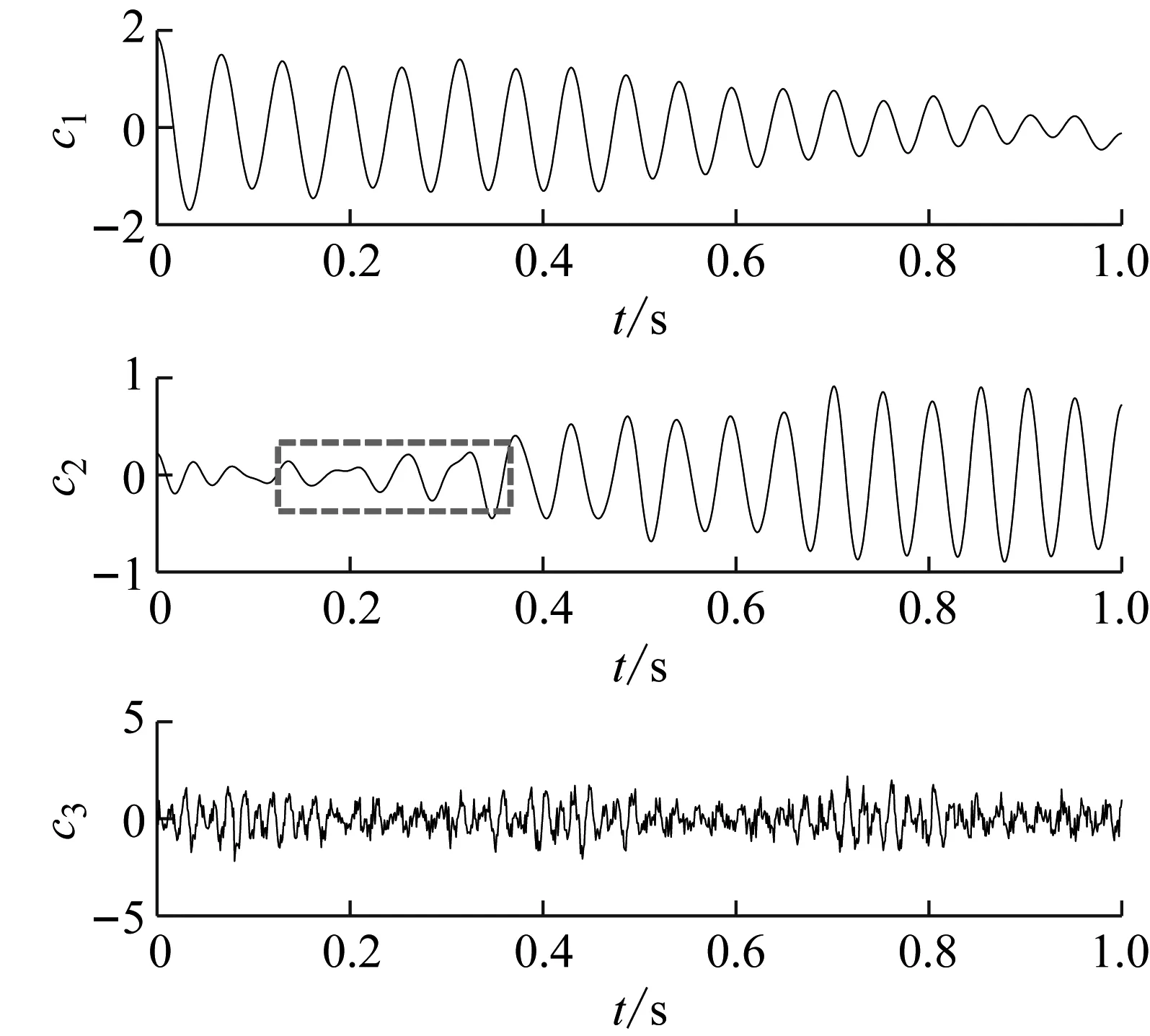
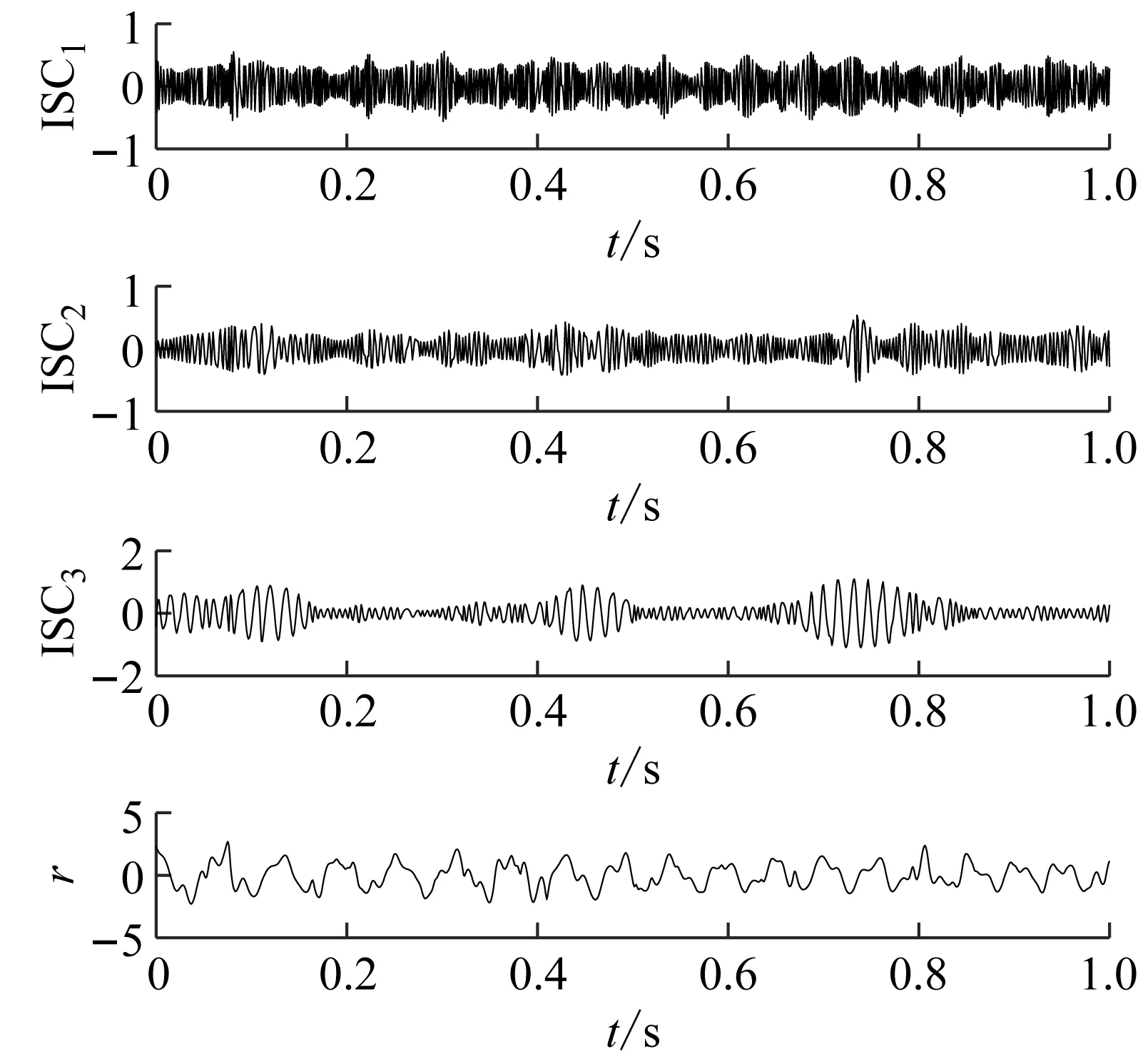
(a) EAEFD(b) EWT(c) EMD(d) LCD(e) AEFD

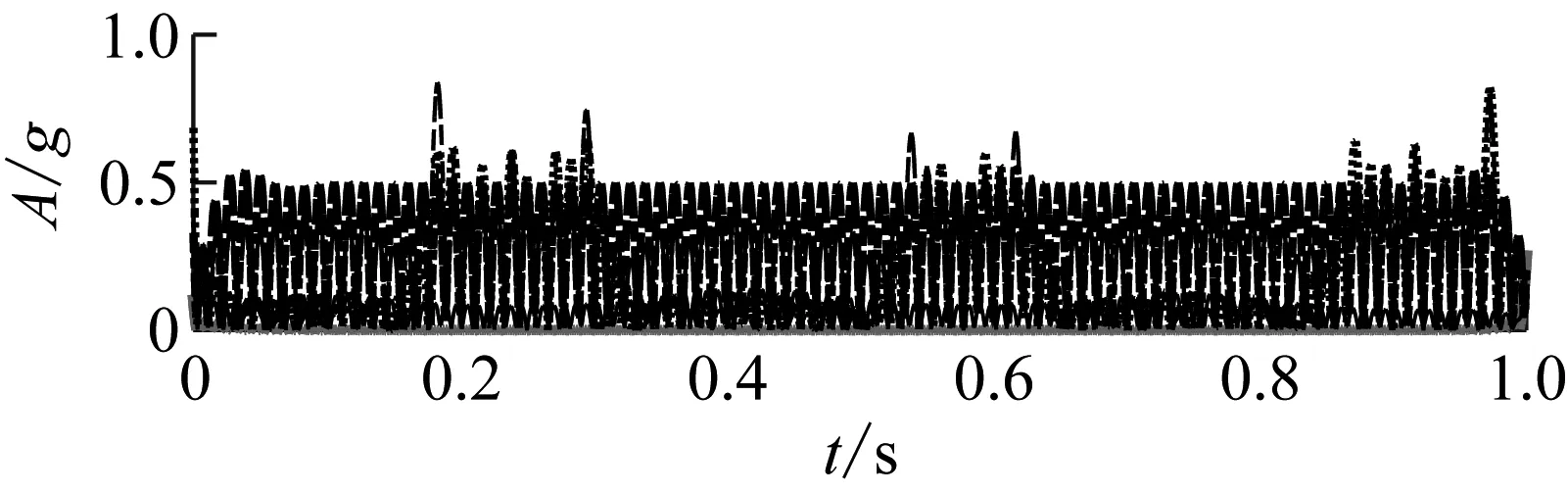
为了对比五种分解方法得到的分量与真实分量之间的吻合程度，由图11所示的绝对误差图可以看出，EWT，EMD，LCD和AEFD方法分解得到的三个分量与真实分量之间的绝对幅值误差均比较大，与这四种方法相比较，EAEFD方法分解得到的三个分量与真实分量之间的绝对幅值误差均比较小，故可以说明EAEFD方法的精确性和抗噪声效果更好，具有一定的优越性。

(a)

(b)

(c)

由表3可知，EAEFD方法分解得到的分量与三个对应真实分量之间的相关系数分别为0.991 36,0.981 99和0.988 64，相关性较高，分别大于EWT方法的0.953 21,0.516 09和0.681 4，EMD方法的0.765 86,0.465 81和0.593 24，LCD方法的0.015 52,0.045 34和0.738 32以及AEFD方法的0.812 62,0.600 79和0.798 68。LCD方法分解得到的三个分量中，前两个分量与真实分量之间的相关系数很小，几乎为零，这说明LCD方法分解效果较差，而EAEFD方法分解得到的分量与真实分量之间的相关系数较大，说明分解效果好，在含噪声的背景下，EAEFD方法与另外四种方法相比，分解效果仍是最优的。

表3 五种分解方法的相关系数的评价指标对比

为了进一步验证EAEFD方法的有效性，计算五种分解方法结果的正交性指标，结果如表4所示。从表4可以看出，EMD和EWT方法分解结果的正交性指标分别为0.158 49和0.141 41，大于LCD方法的0.032 42，以及AEFD方法的2.87×10-17，而EAEFD方法分解结果的正交性指标最小，几乎为零，说明EAEFD方法分解的正交性最好。接下来从误差能量比上来看，EAEFD方法分解得到的分量与真实三个分量之间的误差能量比分别为0.018 13，0.044 09和0.026 24，三个分量的误差能量比均是最小的，分别小于EWT方法的0.094 66，2.297 35和1.241 24，EMD方法的0.474，1.447 02和0.778 31，LCD方法的1.171 56，1.961 11和0.456 84，以及AEFD方法的0.340 45,1.975 20和0.609 29。相比EAFED方法，EWT，EMD和AEFD方法的第二个和第三个分量误差能量比都比较大，LCD方法的第一个和第二个分量误差能量比均较大，故可以说明EAEFD方法的有效性。

表4 五种分解方法的正交性和误差能量比的评价指标对比

综上分析，与EWT，EMD，LCD和AEFD方法相比，EAEFD方法的抗噪能力更强且分解得到的分量在相关性、正交性和精确性等方面均有一定的优越性。

3 实测信号分析

为了进一步验证所提出EAEFD方法的有效性和优越性，将其应用于滚动轴承故障模拟试验台的实测信号数据分析，该试验数据来自安徽工业大学滚动轴承故障试验台，如图12所示。试验台由驱动装置、支撑装置、加载装置以及缓冲装置四部分构成，试验装置中，1号传感器采集径向振动信号，2号传感器采集水平振动信号，3号传感器采集轴向振动信号。试验采用的滚动轴承型号为SKF 6206-2RS1/C3，使用电火花加工技术分别在深沟球轴承上布置了内圈、外圈和滚动体的单点故障，试验选取了内圈故障深度为0.3 mm进行验证，如图13所示，负载为5 kN，采样频率为10 240 Hz，主轴转速为300 r/min，3号传感器采集的轴向振动信号，采集的时间为1 s。计算得转频为fr=5 Hz，故障特征频率为fi=27.15 Hz，振动信号的时域波形如图14所示，从图14可以看出，时域波形冲击成分比较明显，原始振动信号的包络谱图如图15所示，图15中仅能提取一倍故障特征频率fi，而且包络谱图中干扰成分严重，无法有效地诊断其故障类型。

1.变频电机;2.主轴;3.滚动轴承;4.1号传感器;

图13 内圈故障的滚动轴承

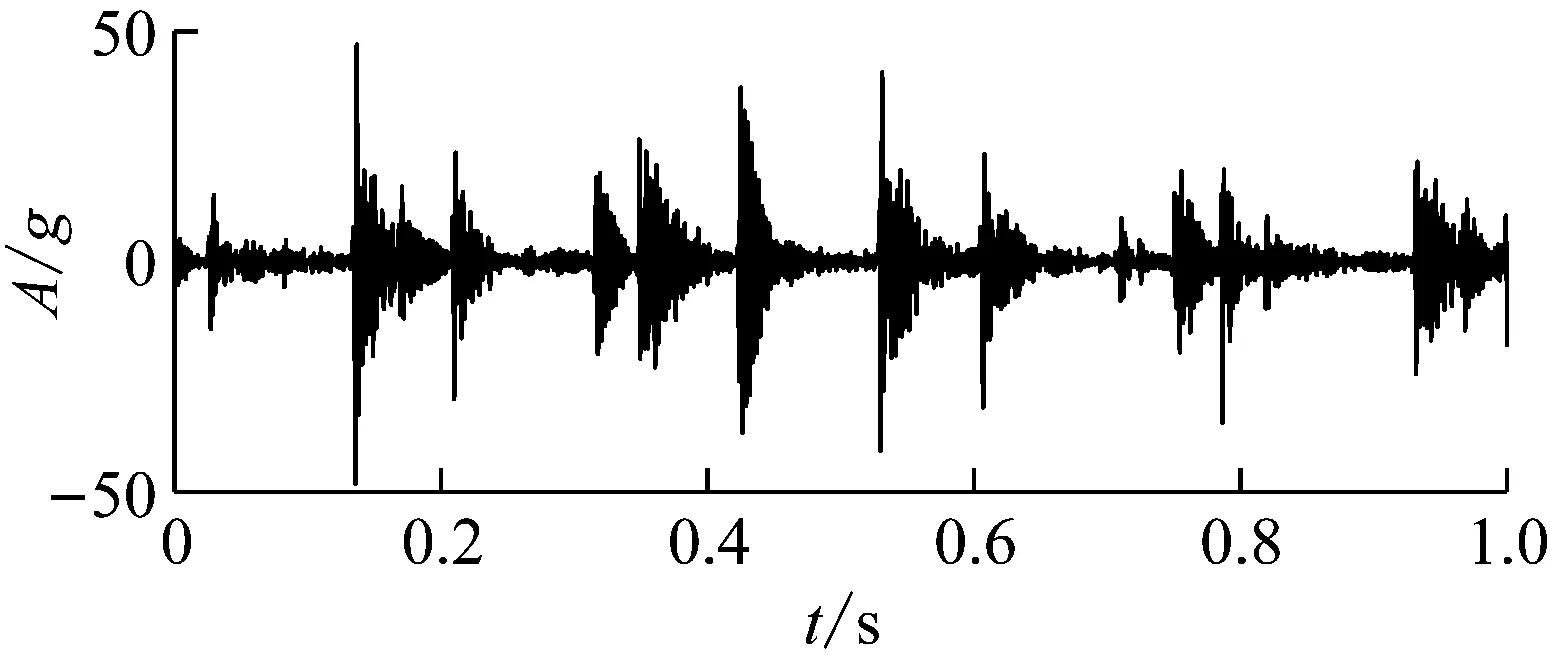
图14 内圈故障的滚动轴承信号时域波形

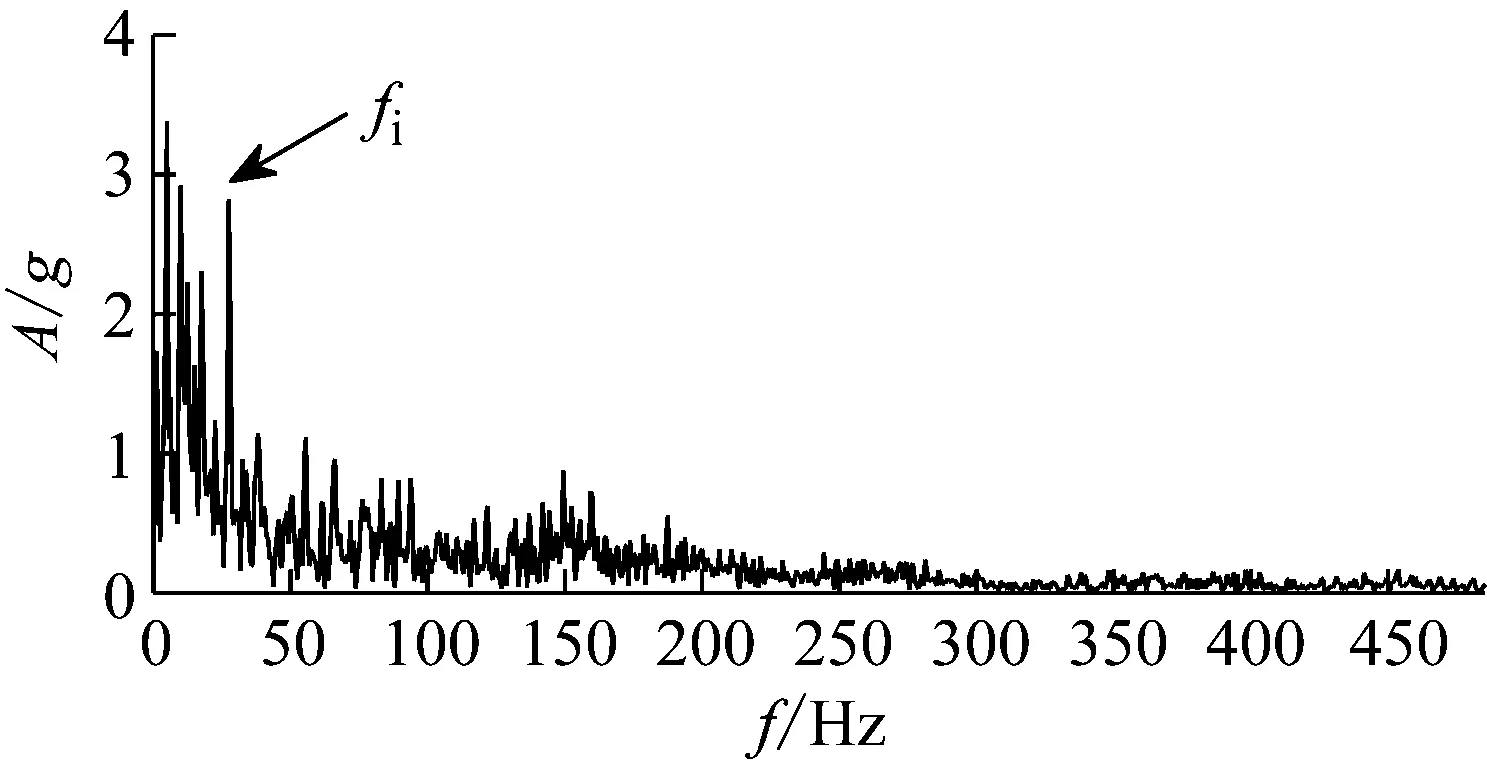
图15 内圈故障滚动轴承信号的包络谱图

首先，采用EAEFD方法对具有内圈故障的滚动轴承信号进行分解，分解的初始化模态数N=2，设定分解模态数N的搜索范围为[2,16],利用包络谱熵值评价指标优化分解的模态数N，得到局部极小熵值随模态数N变化的关系图，如图16所示，当N=9时，取得最小包络熵值为3.745 7，故EAEFD方法分解的最优模态数N=9。

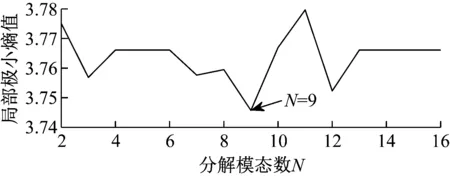
图16 局部极小熵值随分解模态数N的变化情况

由图16可知，EAEFD方法分解的最优模态数N=9，此时频谱的处理次数为四次，为了比较EAEFD，EWT，EMD，LCD和AEFD方法分解的效果，分别采用五种方法对具有内圈故障的滚动轴承信号分解，EAEFD方法分解的个数为九个，AEFD，EWT方法和LCD方法分解的个数为五个，AEFD方法初始边界集设置为[160,380,500,620]，由于EAEFD方法和EMD方法分解的个数均比较多，由于篇幅原因，故取前5个分量，分解的结果如图17(a)～图17(e)所示，EAEFD方法分解得到五个分量具有明显的冲击成分特征，EWT方法分解得到的第一个分量中出现了模态混叠(图中虚框所示)，第五个分量有冲击成分的特征，但不明显，EMD方法分解得到的分量中无明显的冲击成分特征，第五个分量中出现了模态混叠，LCD和AEFD方法分解得到的前四个分量冲击成分特征不明显，第五个分量的冲击成分特征比较明显。与EWT，EMD，LCD和AEFD方法对比，说明了EAEFD方法的有效性和优越性。

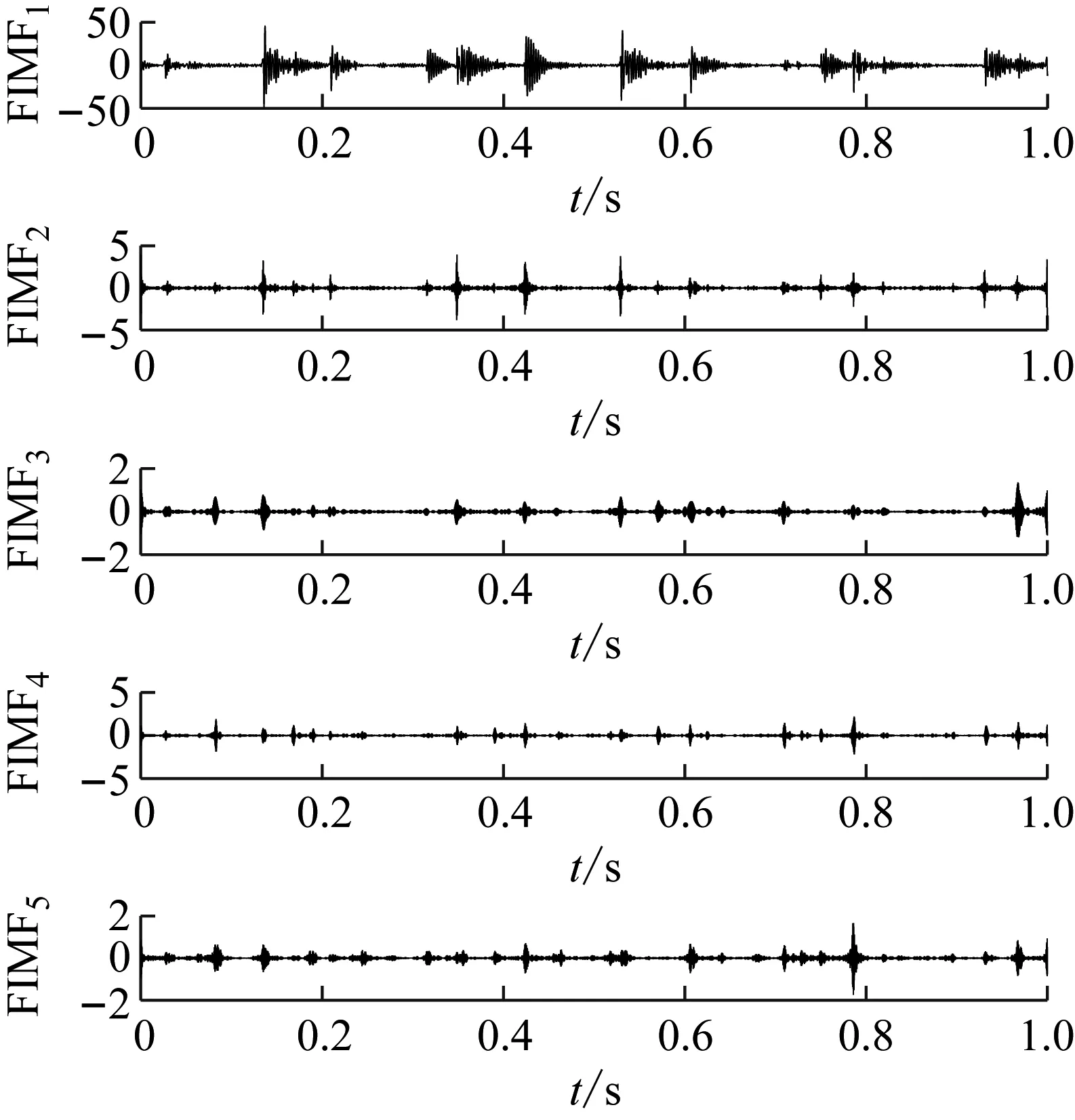
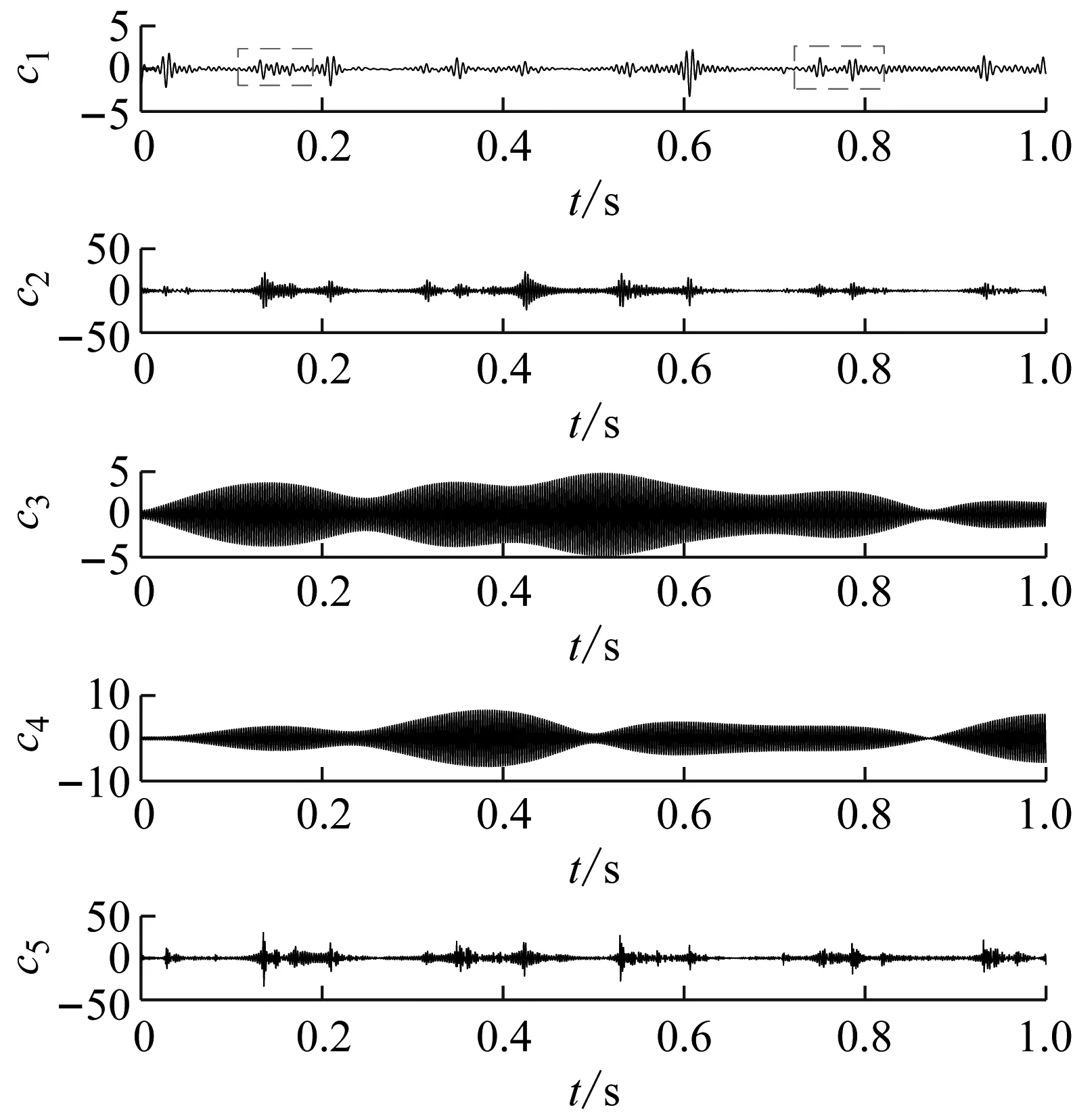
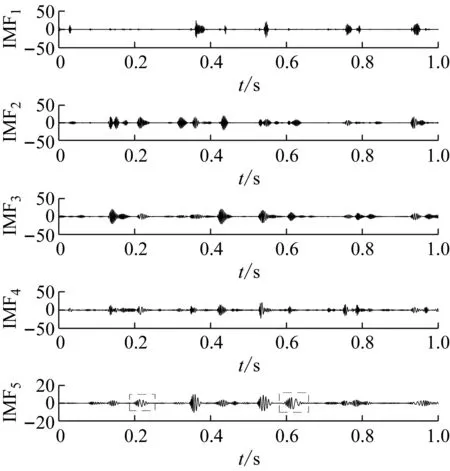
(a) EAEFD(b) EWT(c) EMD(d) LCD(e) AEFD

其次，为了更加有效地提取故障成分特征，分别计算五种分解方法中各个分量的包络谱，由于篇幅原因，文中给出前五个分量包络谱图，结果如图18(a)～图18(e)所示，EWT方法的第一个分量和第五个分量包含内圈故障特征频率fi，第二个分量包含内圈故障特征频率fi及其倍频2fi，而第三个和第四个分量没有包含内圈故障特征频率，对应着时域上第三个和第四个虚假的分量；EMD方法第二个至第五个分量包含内圈故障特征频率fi，而第一个分量没有包含内圈故障特征频率；LCD方法的第三个和第四个分量包含内圈故障特征频率fi，第五个分量包含包含内圈故障特征频率fi及其倍频2fi和3fi，刚好与时域上突出冲击成分特征的第五个分量相对应；AEFD方法第二个至第四个分量包含内圈故障特征频率fi，第五个分量包含包含内圈故障特征频率fi及其倍频2fi；EAEFD方法的第一个和第三个分量中包含内圈故障特征频率fi及其倍频2fi，第二个，第四个和第五个分量中均包含内圈故障特征频率fi及其倍频2fi和3fi，该方法的五个分量中故障特征频率及各阶倍频明显，而且频谱图中各阶倍频处有幅值逐渐下降的谱线，故EAEFD方法可以有效地诊断出滚动轴承的内圈存在故障。

最后，为了定量的比较EAEFD，EWT，EMD，LCD和AEFD方法分解得到的分量提取故障特征频率的能力，采用文献[23]定义的信噪比(signal-to-noise ratio,SNR)(RSN)指标来衡量故障特征的能量比，信噪比越大，噪声干扰就越小，故障特征频率就越明显，信噪比定义为

(11)

式中：P[·]为快速傅里叶变换得到的功率谱;fm为故障特征频率;N为时间序列长度;Δf为频率分辨率。

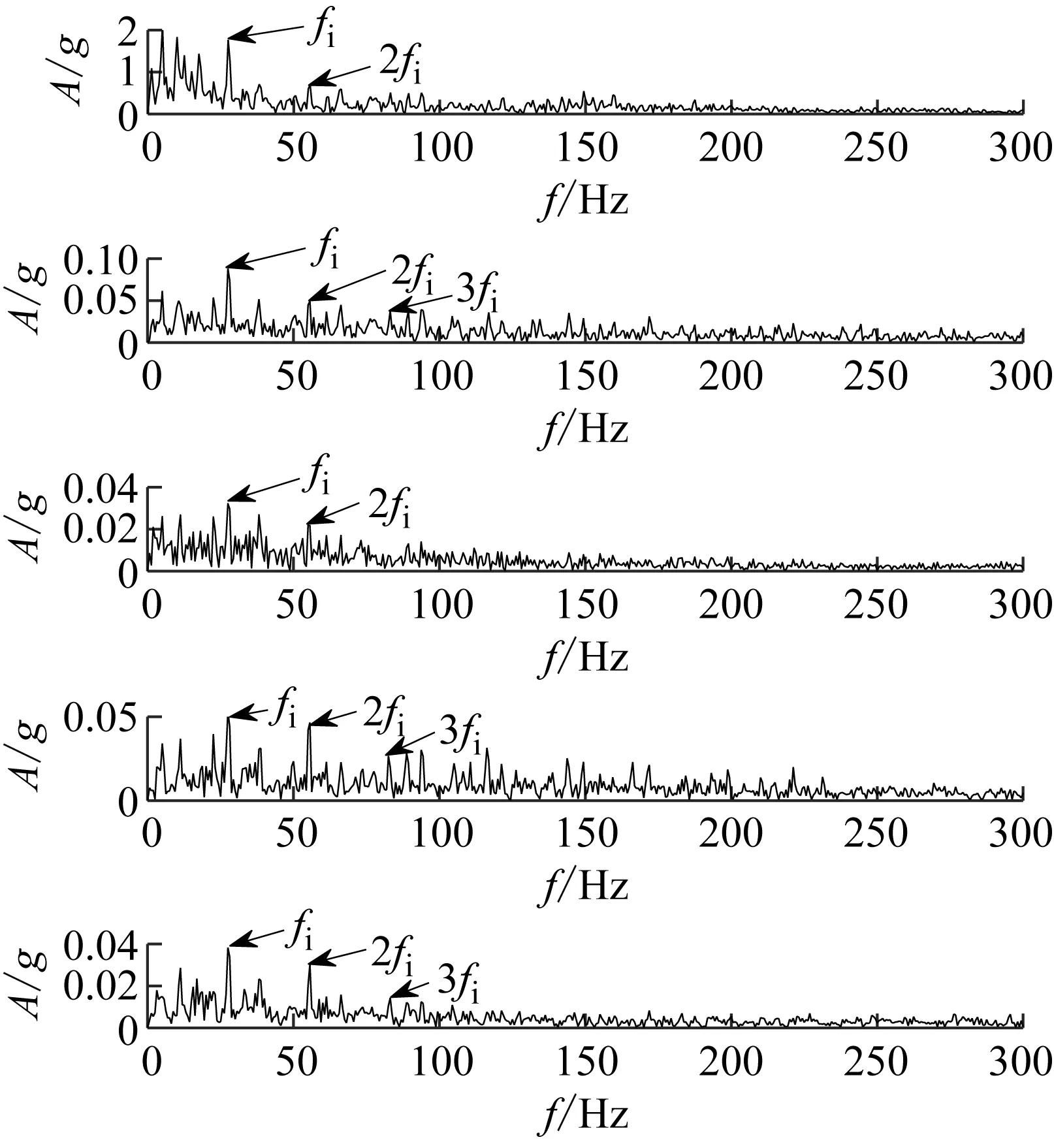
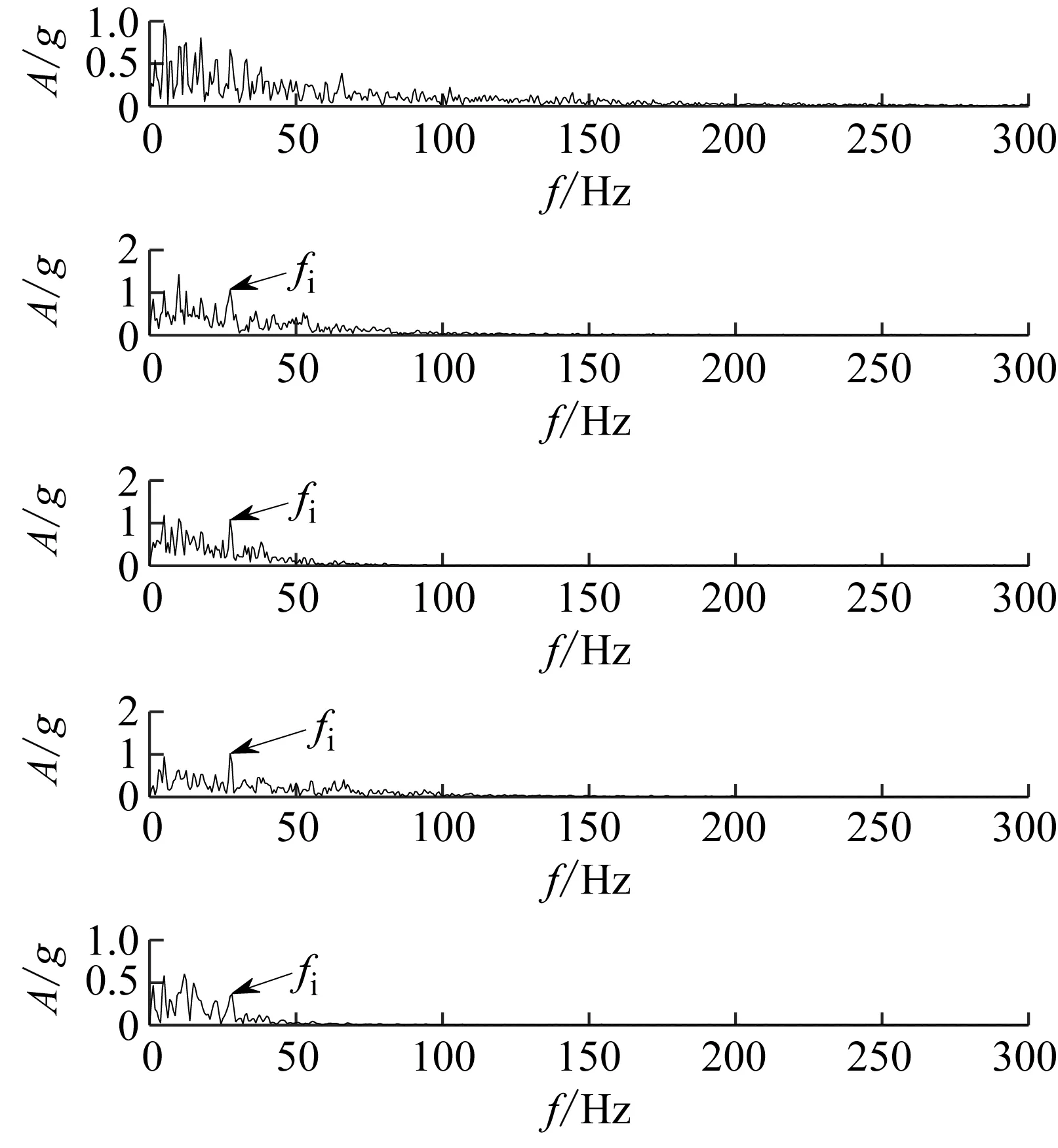
(a) EAEFD(b) EWT(c) EMD(d) LCD(e) AEFD

论文中选择峭度最大的分量计算信噪比，峭度值越大，说明分量包含故障成分越多，其峭度定义为

(12)

式中：y(ti)为在ti时刻内的样本；μx为样本的平均值；N为样本长度。

五种分解方法峭度最大的分量的信噪比计算结果如表5所示，表5中n表示为故障特征频率的倍频，由表5可知，与EWT，EMD，LCD和AEFD方法相比，EAEFD方法分解得到的分量的一倍频，二倍频和三倍频的信噪比均是最大的。表明EAEFD方法定量诊断效果优于其他四种方法，EAEFD方法分解效果相比另外四种方法具有一定的优越性。

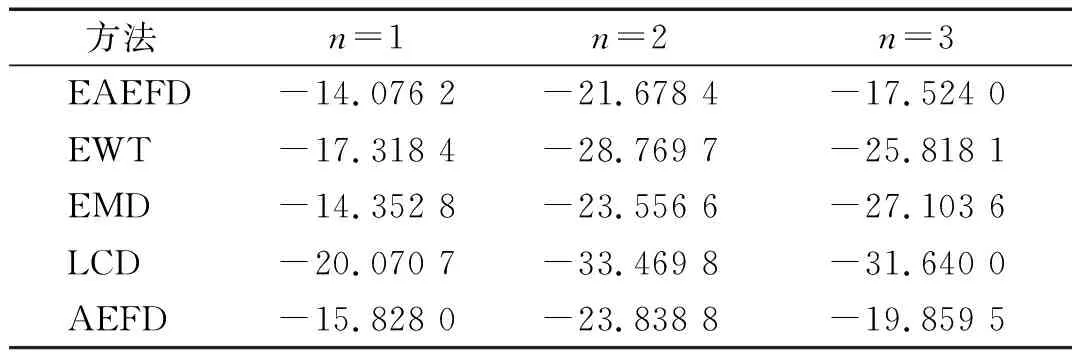
表5 五种分解方法峭度最大的分量信噪比评价指标对比

4 结 论

论文提出了一种改进的自适应经验傅里叶分解方法,并将该方法运用到滚动轴承诊断中，与现有的几种方法对比，得出以下结论：

(1) 理论方面，EAEFD方法与AEFD方法相比，EAEFD方法可以避免人为设置边界集，自适应地确定最优分解模态数；与EWT方法相比，EAEFD方法能够得到一个合理的分割边界；与EMD方法和LCD方法相比，能够有效避免模态混叠问题。

(2) 通过仿真信号分析，将EAEFD方法与EWT，EMD，LCD和AEFD方法进行了对比，实验结果表明，EAEFD方法在分解的相关性，正交性和精确性方面具有一定的优越性，同时还有更强的抗噪能力。

(3) 将EAEFD方法和EWT，EMD，LCD和AEFD方法与包络谱相结合，运用在具有内圈故障的滚动轴承中，实验结果表明，EAEFD方法不仅能够有效地诊断故障，而且诊断精度更高。