解题教学要帮助学生“学会寻找思路”——以李庾南老师习题讲评实录为例

筅江苏省海安市海陵中学 杨亚平

1 引言

最近有机会观摩学习了全国著名特级教师李庾南老师执教的一元二次方程习题课．李老师讲评习题并不满足于学生说出答案、核对解法步骤的层次，而是带领学生全面理解题意，先从整体上看清问题，然后各个击破，最终实现问题解决．本文中先梳理李老师对3道习题的讲评过程，再与同行交流笔者的一些学习体会．

2 李庾南老师讲评3道习题的课堂记录

例1k为何值时，关于x的二次三项式x2-10x+k+5为一个完全平方式？

课堂记录：学生很快得出答案k=20，李老师让其中一个学生讲讲思路．

生1：由完全平方式的结构，我先分析出公式中的b应该是5，所以k+5=52，从而求出k=20．

生1点头认可，李老师追问其他学生，他们也表示是这样思考的．

师：你们还有其他思路吗？

生2：我是用一元二次方程的根的判别式求解的．先假设二次三项式x2-10x+k+5为一个完全平方式，那么它对应的一元二次方程x2-10x+k+5=0可以写成（x+m）2=0的形式，也就是说，这个方程有两个相等的实数根，所以Δ=b2-4ac=0，即（-10）2-4×1×（k+5）=-4k+80=0，解得k=20.

师：很好！活学活用，能运用方程的眼光看待二次三项式ax2+bx+c（a≠0），想到这个式子为完全平方式的条件就是它所对应的一元二次方程的根的判别式b2-4ac=0．

例2当k为何值时，关于x的方程kx2-4x+4=0有实数根？

课堂记录：有个别学生很快就做好了，李老师巡视时发现他是典型的默认本题中的方程是一元二次方程，运用根的判别式求解，出现了漏解的情形，于是李老师安排该生上台讲解他的思路．

生3：由题意可得b2-4ac=16-16k≥0，即k≤1时，原方程有两个实数根．

师：大家同意他的解法吗？

生4：还要考虑k≠0，因为这是一元二次方程．

师：生3，你同意吗？（生3表示忽略了这个限制）生4，问题中有没有明确说明这是一元二次方程？

生4：没有，所以还要分类讨论k=0的情况，也就是说，它有可能是一元一次方程．

师：那你们再全面思考一下，看要考虑哪些可能的情形．

1分钟后，生4示意他已想清思路.

生4：已知条件中并没有明确指出原方程是什么方程，也没有说明有几个实数根，因而必须分类讨论.

李老师根据生4的讲解，在黑板上板书示意：

接着李老师安排学生写出解法，生4上台板演，如下：

①当k=0时，原方程为一元一次方程-4x+4=0，有一根为x=1．

②当k≠0时，原方程为一元二次方程，当b2-4ac=16-16k≥0，即k≤1且k≠0时，原方程有两个实数根．

李老师在学生解答的基础上，提醒学生可以写出结语：

综上，当k≤1时，关于x的方程kx2-4x+4=0有实数根．

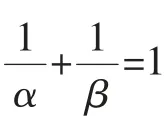
课堂记录：经过2分钟左右，就有学生示意求出了m=3，李老师检查后对结果表示肯定，指导该生再思考如何更严谨地组织语句，又过了1分钟后，安排该生上台讲解．

李老师在学生讲解时，梳理她的思路，形成如下板书：

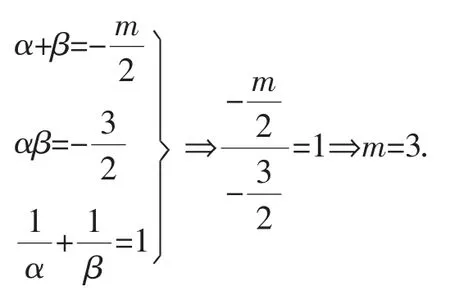
师：大家同意她的解法吗？有没有补充的？

生6：还应该考虑这个方程是否有实数解，也就是要计算一下根的判别式．我算了一下，根的判别式是m2+24，恒大于0，所以这个方程一定有两个不相等的实数根．

李老师对生6的补充表示肯定，并将生6的意见书写在生5的思路的上面，然后整体上用“大括号”括起来，如下板书示意：

李老师随后提醒学生注意在运用一元二次方程根与系数的关系前，要优先考虑一元二次方程的根的判别式．

3 解题教学要帮助学生“学会寻找思路”

3.1 从读题到审题，让学生形成解题“整体观”

观摩李老师的解题教学可以看出，李老师并不是先带领学生一起读题、分析思路，而是让学生先独立解题，在学生有了思路之后，李老师会走到学生旁边个别诊评，然后根据学生的解答情况进行评价或思路点拨，如果是比较典型的“问题解法”，李老师会“捕捉”“采集”出来，让学生到讲台上板演或讲解思路，然后师生共同分析，让学生在反复读题、理解关键条件或题设信息中完善解法．从上面几道习题的讲评看，李老师在学生讲解、优化、补充的同时，会梳理出解题思路，让学生形成解题“整体观”，而不是看见一个条件就急于演算，结果思考不全面而导致解题不严谨或有错漏．这里特别值得一说的是，所谓解题“整体观”［1］，即审题要仔细，看清所有题设信息，而不是盯住某个条件“仓促上路”；或者从结论逆向出发，接通某个题设条件就以为思路贯通、解题成功，这样的解题常常是缺少“整体观”的体现．从这个意义上说，李老师的习题讲评过程体现出来的“整体观”是值得我们学习的．

3.2 从听讲到对话，让学生解题“严谨而简明”

目前的初中数学课堂教学中，习题讲评课占很大比例，不少日常习题讲评课往往是教师讲题为主，有些即使安排学生讲题，也多是用学优生的嘴代替教师的讲解（有些专家认为还不如教师亲自讲解）．我们看到专家教师李庾南老师的习题讲评课就从学生单纯听讲走向了生生对话、师生对话．从上文分享的3道习题的讲评过程，可以看到一些高品质的师生对话，更多学生的思维都被卷入对话中．特别是，李老师在学生讲评或对话的过程中，及时采集、梳理学生的思路，用体现“整体观”的板书形象、生动地再现学生的思路历程，帮助学生展现他们解题过程中“火热的思考”．在师生充分对话和交流之后，学生基于对问题解决的“整体观”，只要列出相应的关系式或方程组，然后简明写出各步结果，最后给出结语即可，对较难题来说，让学生懂得“省略非必要表达步骤”是使过程表达简明的重要技能［2］．

3.3 从纠错到究错，让学生感悟“细节决定成败”

从李老师组织的3个习题讲评实录来看，李老师善于捕捉“生成性资源”，并且那些解题速度快但有“错漏”的学生往往容易被李老师安排先上台展示，接着李老师并不急于进行纠正、订正，而是以一个“促动师”的角色，组织学生讨论、对话，在这个过程中，往往原来出错的学生会发现他的错漏就在于“某个细节”没有注意到，这些细节都在纠错中实现了究错［3］．事实上，这样的教学过程正是著名小学数学特级教师华应龙老师所倡导的“化错教学”．

自20世纪70年代末李庾南老师提出“自学·议论·引导”教学法以来，该教学法在新授课、单元教学的相关主题研究方面都比较丰富，但是关于“自学·议论·引导”教学法在习题课教学中的实践，还有待进一步深入研究．本研究是笔者近期有机会观摩学习李老师在习题课中的一些精彩实录后的有感而发，有些观点和感悟不一定准确，更不一定正确，期待专家、同行的批评指正．