高斯白噪声下非对称单稳态能量采集系统的随机响应分析

刘迪，胡美

（山西大学 数学科学学院，山西 太原 030006）

0 引言

由于压电振动能量采集装置可将周围环境中废弃的动能转化为电能，因此其动力学行为吸引了越来越多的关注。研究发现，相对于线性系统这种仅适用于窄频的固有频率，非线性系统能有效地提高固有频率，进而表现出更好的能量采集效果[1]，其非线性动力学响应分析成了研究热点。

非线性系统由于参数不同，可表现出单稳、双稳等丰富的动力学现象。基于这些现象，国内外研究者发展了不同的能量采集模型，并分析其动力学行为。Stanton等[2]分析了双稳态非线性振子的动力学响应。Abdelkefi等[3]讨论了直接谐和激励下非线性压电耦合对能量采集性能的影响。赵健等[4]用多尺度法研究了非线性微幅受迫磁性能量采集器的稳态响应，并用Runge-Kutta法验证了方法的有效性。李海涛等[5]用Melnikov方法分析了双稳态压电能量系统的分岔和混沌等非线性行为，为弱非线性双稳态系统的参数设计提供了指导。Xu等[6]使用标准随机平均法研究了双稳态能量采集系统的随机响应。

大量关于非线性压电能量采集的研究都是针对系统具有对称势能函数的情况。而在实际的操作中，由于装置的制作误差及工作环境的改变都会导致其系统势能函数非中心对称，进而使动力学行为发生本质改变。Wang等[7]用细致平衡法研究了非对称多稳态能量采集器的随机响应。Daqaq等[8]利用统计线性化和有限元法发现了非对称单稳态和双稳态能量采集系统在白噪声作用下其平均输出功率呈现出相反的表现。Zhou等[9]用谐波平衡法和Jacobi矩阵对非对称三稳态能量采集器进行了动力学分析。

然而，目前针对具有非对称势能函数的能量采集系统的研究大多是基于数值模拟方法[10-14]，无法从本质上揭示非对称能量采集系统的各个物理量对系统的动力学行为的影响。而基于平均原则[15]的随机平均法由于能解析地获得非线性随机系统的响应受到了广泛关注，最近这种方法被进一步发展并应用到具有对称势能函数的压电能量采集系统的研究上[16-17]。因此本文针对三次非线性压电能量采集系统，基于坐标变换的拟保守随机平均法，建立了随机激励下的具有非对称单稳态系统的FPK方程，并求解其相应的稳态概率密度，进而得到均方电压和平均输出功率的表达式。通过直接Monte Carlo模拟验证了本文提出方法的有效性，随后进一步研究了非对称单稳态系统在高斯白噪声激励下的稳态随机响应。

1 非对称单稳态能量采集系统

考虑高斯白噪声下的非对称单稳态能量采集系统

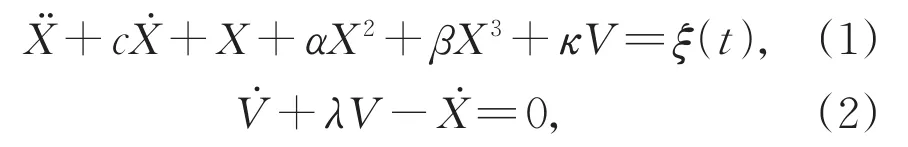
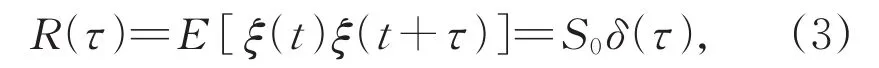
其中δ(τ)是一个狄拉克函数；τ是相关时间。系统（1）的势能函数为U(X)=1 2X2+1 3αX3+1 4βX4，由图1可知α的增加将导致势能函数U(X)的不对称程度的增加。

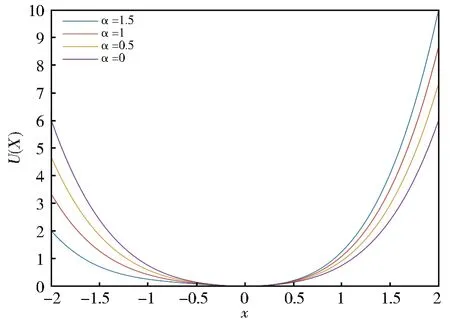
图1 β=1时α对势能函数的形状和对称度的影响Fig.1 Influence ofαon the shape and symmetry of the potential function forβ=1

2 等效非对称单稳态能量采集系统

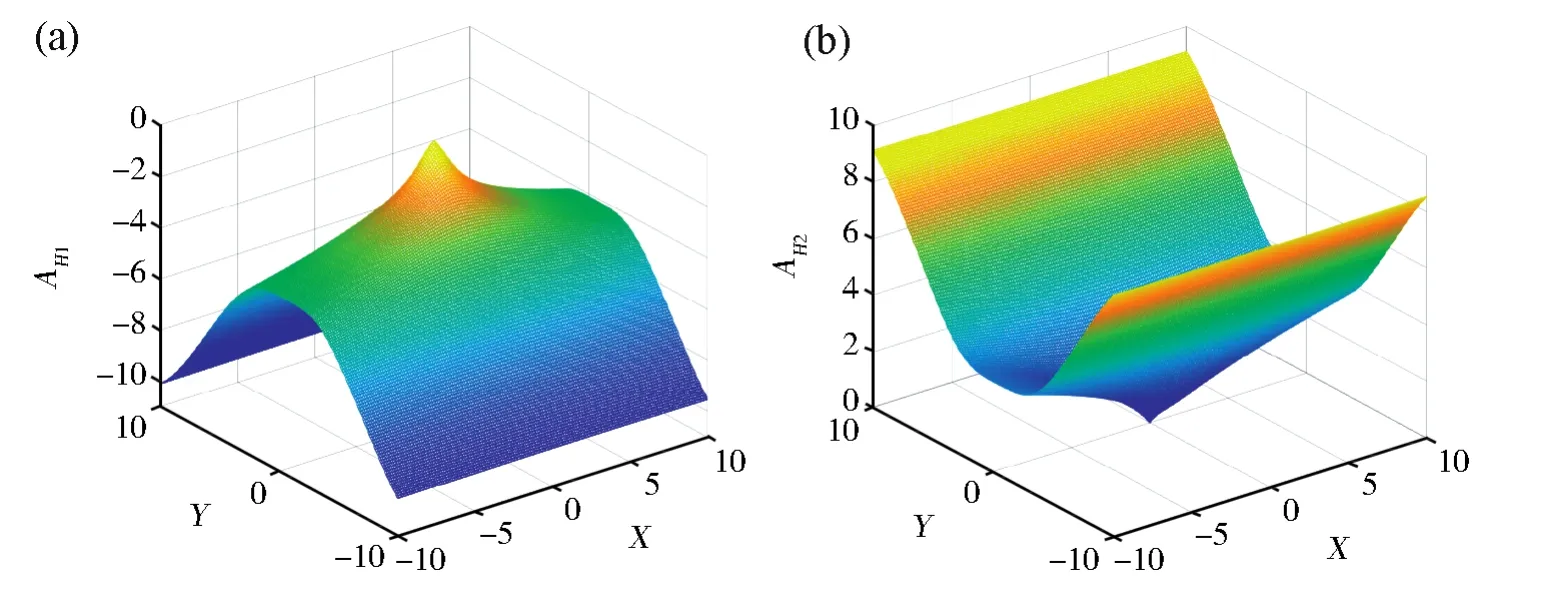
图2 （a）最小位移AH1；（b）最大位移AH2Fig.2 (a)Minimum displacementAH1;(b)Maximum displacementAH2

3 拟保守随机平均法

4 数值结果和随机分析

为了验证第3节给出的基于坐标变换的拟保守随机平均法的有效性，以及分析系统各个物理量变化对均方输出电压的影响程度，给定系统参数c=0.02，α=1.5，β=1，κ=0.5，λ=0.1 和噪声强度S0=0.01。系统位移和速度的联合概率密度函数如图3所示，图3（a）是通过拟保守随机平均法得到的结果，此结果与直接Monte Carlo数值模拟的结果相一致（见图3（b）），这证明了基于坐标变换的拟保守随机平均法的有效性。图4给出了位移和速度的边际概率密度函数图像，其中线条表示由本文所提出方法获得的解析结果，星号为Monte Carlo数值模拟的结果，通过对比可以看出两个结果相吻合，这再次表明了本文所提出的拟保守随机平均法可以用于研究非对称单稳态系统的随机响应问题。

图3 位移和速度的联合概率密度函数p(X，Ẋ)。（a）解析结果；（b）Monte Carlo结果Fig.3 Joint PDF of the displacement and velocityp(X,Ẋ).(a)analytical result;(b)MC result

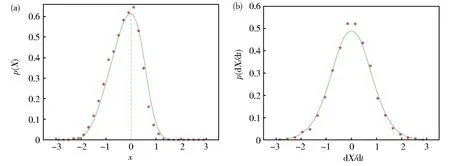
图4 （a）位移X的边际概率密度函数p(X)；（b）速度Ẋ的边际概率密度函数p(Ẋ)Fig.4 (a)The marginal PDFp(X)of the displacementX;(b)The marginal PDFp(Ẋ)of the velocityẊ

图5和图6给出了不同物理量对均方电压的影响，并通过Monte Carlo模拟验证了解析结果，图中线条表示解析结果，圆圈表示Monte Carlo数值模拟的结果。其中，图5为噪声强度S0、阻尼系数c、非对称度α和三次非线性系数β对均方电压的影响，可以发现噪声强度S0和非对称度α的增加均会引起均方输出电压的增加。但是，随着阻尼系数c和三次非线性系数β的增加，均方电压会迅速的减少。通过平均输出功率和均方输出电压的线性关系可以得到，非对称度和噪声强度有利于提高非对称单稳态系统收集能量的效率，而阻尼系数和三次非线性系数对系统的能量收集性能会起到阻碍作用。图6为参数λ和机电耦合系数κ对均方电压的影响，可以发现参数λ和耦合系数κ的增加都会导致均方电压的减少。

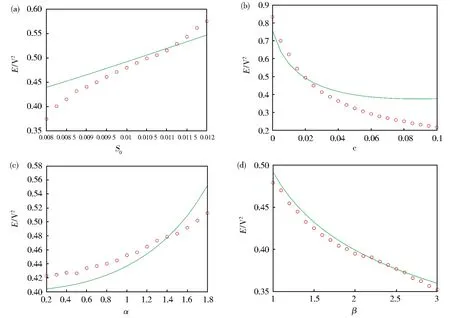
图5 （a）噪声强度S0对均方电压E[V2]的影响；（b）阻尼系数c对均方电压E[V2]的影响；（c）非对称度α对均方电压E[V2]的影响；（d）三次非线性系数β对均方电压E[V2]的影响Fig.5 (a)Dependence of the MSOVE[V2]on the excitation intensityS0;(b)dependence of the MSOVE[V2]on the damping coefficientc;(c)dependence of the MSOVE[V2]on the asymmetry degreeα;(d)dependence of the MSOVE[V2]on the cubic nonlinearity coefficientβ

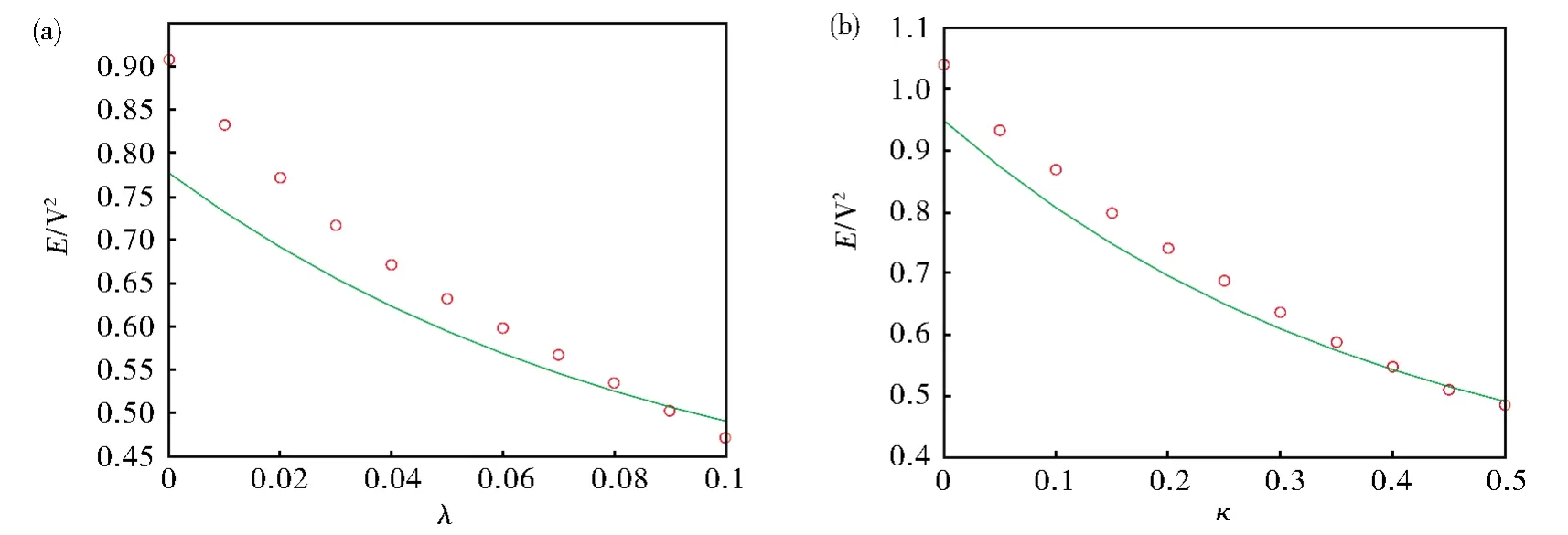
图6 （a）参数λ对均方电压E[V2]的影响；（b）机电耦合系数κ对均方电压E[V2]的影响Fig.6 (a)Dependence of MSOVE[V2]on the parameterλ;(b)dependence of MSOVE[V2]on the electromechanical coupling coefficientκ

5 结论

本文的目的是研究高斯白噪声下非对称单稳态能量采集系统的随机响应。首先，通过引入坐标变换，应用拟保守随机平均法得到了关于总能量的Itô随机微分方程，并在Markov近似下得到其相应的FPK方程。接着，通过求解FPK方程获得了其稳态概率密度函数的解析表达式，进而获得系统的均方输出电压和平均输出功率。然后，利用一个实例验证了该研究方法的有效性。通过对比分析在不同的噪声强度以及非对称度下系统的均方输出电压，发现噪声强度及非对称度的增加都可以导致均方电压的增加，提高系统的能量采集效率。然而，在对不同的阻尼系数以及三次非线性系数下系统的均方输出电压进行对比分析，发现这两个物理量的增加会引发均方电压的减少，对能量采集效率起到抑制作用。最后，采用Monte Carlo方法进一步数值验证了上述分析结果的准确性。相关研究结果不仅为单稳态能量采集系统的设计及应用提供了一定的理论指导，并为后续非对称双稳态能量采集系统的研究方法提供了思路。