基于推理能力 探求最短路径——以“最短路径问题”教学为例

湖北省武汉市将军路中学 王 琼

湖北省武汉市吴家山第三中学 万建光

1 引言

最短路径问题是八年级“轴对称”一章章末的课题学习，引导学生探究线段的不等关系，这一内容是初中数学教师的教学中浓墨重彩的一笔.关于最短路径模型的应用、拓展及变式的研究成果非常丰富，对求最值问题中点和线的各种情况的解题策略都有详尽归纳，学生运用这些方法解题也能得心应手.纵观一些“最短路径问题”的公开课，执教者从经典的将军饮马故事入手，让学生经历建模、化归、证明、应用的学习过程，学生能够熟练运用轴对称解决最短路径问题并进行迁移.课后仔细想一想，在这个过程中，执教者往往凸显解决问题过程中的化归思想，而忽略了学生思维中的推理成分.在对问题进行推理的过程中只重视发展学生的演绎推理能力，而忽略合情推理能力的培养.学生的作图方法是通过模仿、操作和记忆来完成的，掩盖了知识的发生、发展过程，限制了学生的推理能力发展.

当然，人们发现知识的曲折过程不可能让学生在有限的一节课时间亲身体验，但教师应该在遵循学生认知规律的基础上，精心设计教学活动，让学生经历知识形成的关键性过程.

2 教学流程

活动1：初识路径，建立模型.

问题1：如图1，将军从指挥部A地出发，到一条小河l边饮马，然后到河对岸的军营B地，那么到河边什么地方饮马可使他走的路线全程最短？

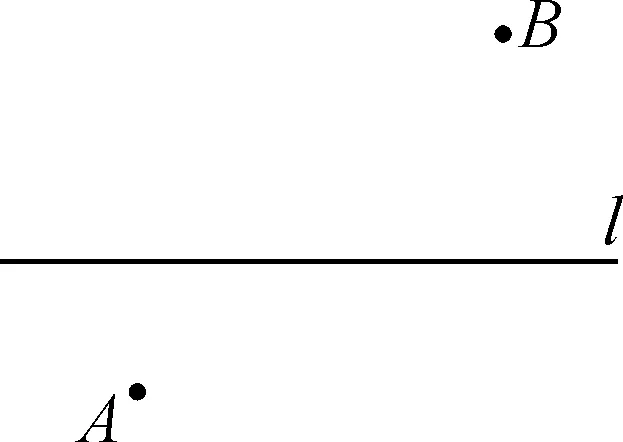
图1

(1)建立数学模型，将实际问题转化为数学问题“在直线l上找一点C，使AC+BC最短”；

(2)如何作图：如图2，连接AB交直线l于点C，点C即为所求；

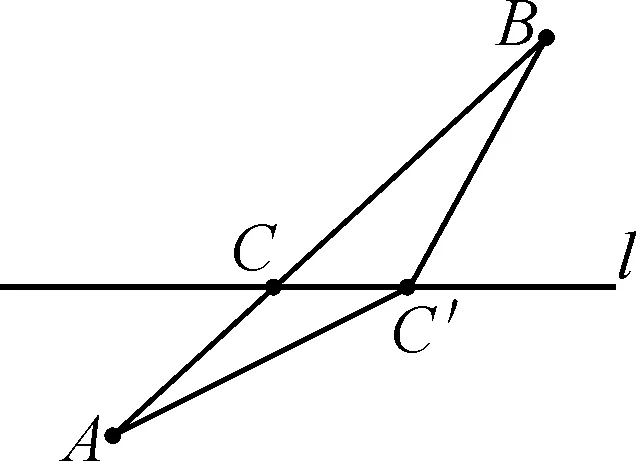
图2

(3)证明AC+BC最短：如图2，运用“三角形的两边之和大于第三边”或者“两点之间线段最短”，这两个结论实质是一个道理；

(4)归纳图中点和线的位置关系，并总结方法“化折为直”.

设计意图：通过设计这个活动，让学生运用已有的知识经验解决这个问题，并引导学生进行推理证明，将学生的直观经验给出严谨的逻辑证明.同时，后面的两个问题都可以化归为这个模型，为学生后续推理提供依据.

活动2：再识路径，猜想证明.

问题2：如图，牧马人从A地出发，到一条笔直的河边l饮马，然后到B地，牧马人到河边的什么地方饮马，可使所走的路径最短？

(1)观察：几何画板演示，如图3.

图3

①在图中拖动直线l的位置；

②拖动直线l上的点C，计算AC+BC的值.

如图4，观察在点C处取最小值时，直线AC和直线BC的位置关系是什么？

图4

(2)猜想：如图5，两点“移”到直线l的异侧得到最短路径.

图5

(3)尝试作图.

(4)如图6，学生证明AC+BC最短.

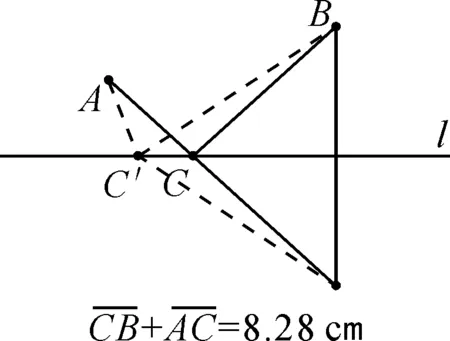
图6

(5)引导学生归纳：通过轴对称作图，将直线同侧两条线段化为直线异侧两条线段求得最短路径.

设计意图：通过几何画板演示，拖动直线l的位置，将问题1中的情境改变为直线同侧两点，与学生原有的认知产生冲突.继续拖动点C在直线l上的位置，演示最短路径时的位置，通过观察直线AC和直线BC的位置关系，让学生认识到，轴对称在化归过程中起到桥梁作用.学生通过观察、猜想后获得解决问题的方法，最后通过逻辑证明，让学生深切体会到轴对称变换的作用，即将直线同侧两点中的一点映射到另一侧，而不改变路径的总长度.

活动3：深悟方法，类比迁移.

问题3：(造桥选址问题)如图7，A和B两地在一条河的两岸，现要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短？(假定河的两岸是平行的直线，桥要与河垂直)

图7

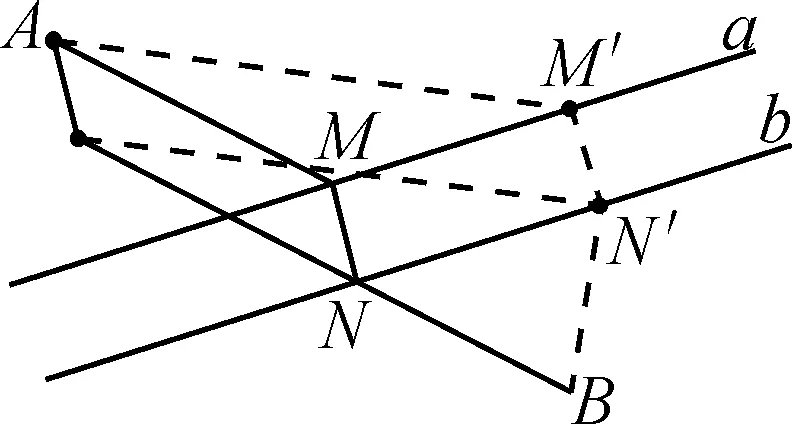
图8

(1)几何画板演示，观察最短路径AM+MN+NB时线段的位置关系和大小关系？

(2)如何转化线段的位置构成两点之间线段最短基本模型？

设计意图：类比问题2的探究过程，在拖动线段MN的过程中，找到最短路径时的位置，观察线段AM，MN和NB的位置关系和大小关系，学生很容易观察到MN为定值，AM与BN平行，通过平移变换，将线段AM平移到线段A′N,根据平行四边形的性质，线段MN平移到线段AA′；同理，将线段NB，平移到MB′,MN则平移到BB′.这样，将问题3化归为问题1的模型.虽然观察到AM与BN平行，但在作图过程中，应该先将定值MN平移，构造平行四边形，完成线段转化.这个过程中注意引导学生分清变换前后的对应点和对应线段，完成最后的证明.

活动4：全面梳理，反思推理.

(1)“两点之间，线段最短”的依据是什么？

(2)我们如何找到轴对称或平移的方法来转化线段的？

(3)什么情形下用轴对称的方法？什么情形下用平移的方法？

设计意图：关注学生的推理活动过程，引导学生梳理解决最短路径问题的知识准备、方法探索、方法应用及辨析过程，明确合情推理和演绎推理在推理过程中的作用.

3 教学分析

推理一般包括合情推理和演绎推理.在解决问题的过程中，两种推理功能不同，相辅相成：合情推理用于探索思路，发现结论；演绎推理用于证明结论[1].国际学生评价项目(PISA2009)将推理能力分为三个水平：再现、联系和反思[2].

3.1 建立模型，实现再现

建模的过程实质上也是一个推理的过程，模型的建立为学生的推理提供“再现”的内容.本节课中学生很容易运用已有知识和经验“两点之间，线段最短”解决这个问题，通过这个模型解决后续问题.但是我们更应该关注这个模型背后的数学思考.人教版初中数学教科书七年级上册将这个结论定义为“一个基本事实”，本质上是对这个结论的合情推理，而七年级的学生缺乏相应的知识来证明这个结论.八年级的学生通过对三角形的知识学习过程，已具备一定的演绎推理能力，可以完成对这个结论的证明.这个模型的建立为学生后续的推理提供了依据，使学生推理过程中有能力对已有知识“再现”.

3.2 操作证明，辨析联系

著名数学教育家斯滕伯格基于自身的教学实践认为：培养推理能力的有效方式是将操作、实践性思维与分析、概括性思维有机地结合起来[3].

合情推理强调动手操作、实验探索等体验性活动内容.学习过程中，学生应当有足够的时间和空间经历观察、实验、猜测、计算、证明等活动过程.在初中数学教学中，观察、归纳、猜想这样的学习方式常常被用于代数的计算法则和数式规律的探索中，几何推理常常侧重于逻辑证明.本课中，通过观察几何画板演示并计算最短路径的过程最终确定最短路径时的位置，帮助学生积累经验，增强感知，发展直觉；通过观察最短路径时线段的位置关系获得猜想，找到转化线段位置的方法，让学生感悟到知识的形成过程.

在实践操作中探索得出的结论，需要用演绎推理的方式加以证明.教师要引导学生对猜想进行证明，并用语言清晰、有条理地表达自己的想法，做到言之有理，落笔有据.

问题3的解决既是推理过程的重现，又是推理能力的提升.学生在已有解决问题2的经验基础上，尝试独立进行推理，让他们自己把握推理过程中的种种关系，从一个数学问题的解决过程中，掌握研究一类问题的方法，正是我们需要培养的数学思维品质.同样通过演示操作确定思路，数学表达完成证明.此时，要引导学生进行辨析，避免学生再度使用轴对称方法而误入歧途.因此，在教学中，要重视引导学生对比情境之间的异同及相关模型、知识、方法之间的关联，建立更准确的“联系”.

3.3 反思推理，形成方法

在教学中，教师应重视引导学生对推理过程和推理结果两个方面进行反思.通过思考“我们如何找到轴对称或平移的方法来转化线段”，即通过观察、猜想探索方法，然后通过证明验证方法的正确性，由此完成对推理过程的反思.通过思考“什么情形下用轴对称的方法？什么情形下用平移的方法？”这个问题，总结点与线的位置关系与选取方法的联系，对推理的结果进行反思.这个“反思”的过程，需要学生对整个推理活动进行总结和提炼，这个过程本身也是一个推理活动.

同时通过反思获得推理的一般性方法，暴露推理过程的思维活动，为后续学习过程中的推理活动提供依据.

推理能力的培养应贯穿于整个数学教学过程中.在教学中，教师要充分发挥合情推理和演绎推理在思维过程中的作用，引导学生在推理活动过程中“大胆猜想，小心求证”，既重视学生思维结果的严密性，又要注重思维过程的探索性，更需要学生孜孜不倦地在尝试中自主建构，提升推理能力.