巧作垂线 构造全等——一道含45°角问题的多解探讨

黄冈师范学院数学与统计学院 程 晶

黄冈实验中学 张 庆

1 引言

波利亚说：解一道题就像建造一所房子,我们必须选择合适的材料.但光收集材料还是不够的,一堆砖头毕竟还不是房子[1].要构筑房子或构筑解,我们还必须把收集到的各个部分组织在一起使它们成为一个有意义的整体.在本市初二年级期末监测中,由于最后一道压轴题最后一问似乎难度极大,于是本市数学教研群中,许多数学老师纷纷就本题交流自己的想法,一次函数、勾股定理、相似三角形、三角函数、四点共圆等初二上学期还未学习的知识出现在解题交流中,难道本题超出了学生的知识范围？标准答案添加了较多的辅助线,证明了四次全等,学生在考场上很难有耐心和信心去完成.不同年级的学生如何去解答这道题？本文中将从几个视角给出一些尝试的解法,试图为含45°角问题提供一般性的解法.

2 试题呈现

在平面直角坐标系中,点A(a,0),点B(0,b),已知a，b满足|a+4|+b2+8b+16=0.

(1)求点A和点B的坐标;

(2)如图1,点E为线段OB的中点,连接AE,过A在第二象限作AF⊥AE,且AF=AE,连接BF交x轴于点D,求点D和点E的坐标；

图1

(3)在(2)的条件下,如图2,过E作EP⊥OB交AB于P,点M是射线EP上一点,且ME=2PE,连接MO,作∠MON=45°,ON交线段BA的延长线于点N,连接MN,求点N的坐标.

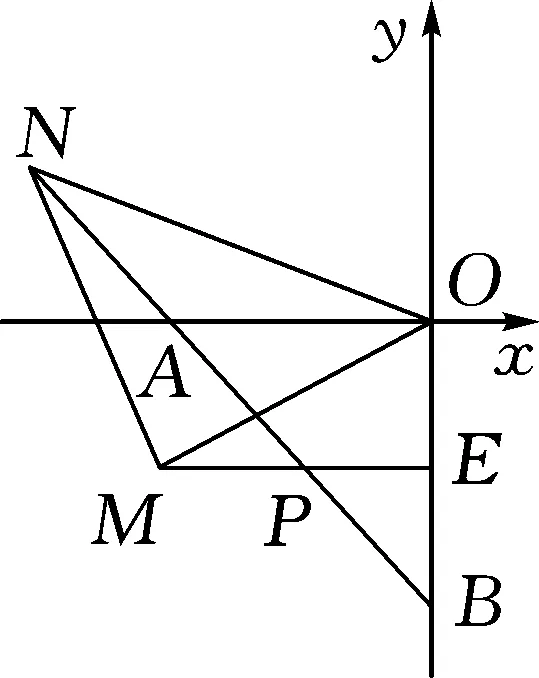
图2

3 试题分析

本题的第(1)、(2)问难度不大,下面着重分析第(3)问,其难点在于证明∠NMO=90°或∠ONM=45°.如何突破这个难点,巧妙地添加辅助线是关键.含45°角的直角三角形有许多特殊的性质,如两锐角都等于45°，两直角边相等，由直角顶点向斜边作垂线可得三线合一，三边长度的比值可以确定，可以构造三垂直证全等三角形，等等.

由题目条件可得E(0,-2),B(0,-4),A(-4,0),OA=OB=4，OE=EB=2，∠ABO=∠OAB=45°，MP=PE=2,△PEB为等腰直角三角形,∠EPB=∠MPN=45°，∠ONA=∠OMP=∠AOM.

4 试卷的参考答案

(1)易得A(-4,0),B(0，-4).

(2)如图3,过点F作FH⊥AO于点H.

图3

因为AF⊥AE,所以易得

∠FHA=∠AOE=90°,

∠AFH=∠EAO.

又因为AF=AE，所以△AFH≌△EAO(AAS).

于是AH=EO=2,FH=AO=4.

则OH=AO-AH=2,因此F(-2,4).

因为OA=BO,所以FH=BO.

又因为∠FHD=∠BOD=90°,∠FDH=∠BDO,

所以△FDH≌△BDO(AAS).

于是HD=OD=1.因此D(-1,0).

综上知,D(-1,0),F(-2,4).

(3)解法1:如图4,过点N分别作NQ⊥ON交OM的延长线于点Q,NG⊥PN交EM的延长线于点G,

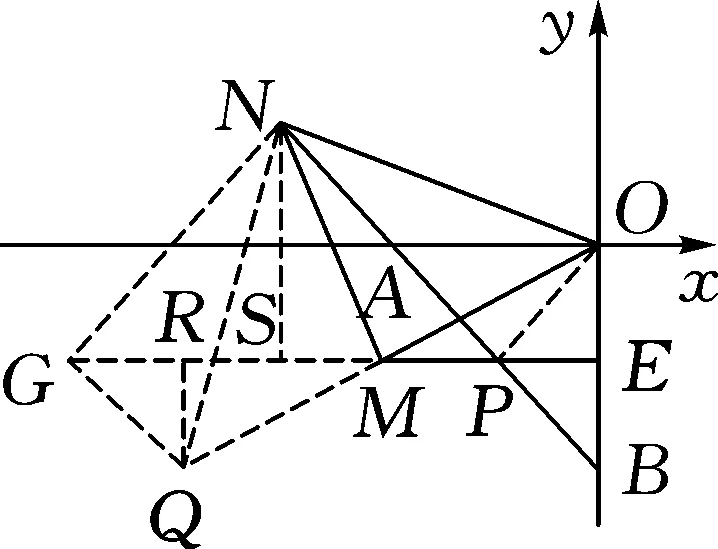
图4

再过点Q和点N作QR⊥EG于点R,NS⊥EG于点S.

则易证得等腰Rt△ONQ和等腰Rt△PNG.

所以NG=NP,NQ=NO,且∠QNG=∠ONP.

所以△QNG≌△ONP(SAS).

于是∠NGQ=∠NPO,GQ=PO.

因为PE垂直平分OB,所以PO=PB.

所以∠POE=∠PBE=45°,因此∠NPO=90°，∠NGQ=90°,∠QGR=45°.

又因为GQ=PO,∠QRG=∠OEP=90°,所以△QRG≌△OEP(AAS),QR=OE.

因为∠MRQ=∠MEO=90°,∠RMQ=∠EMO,

所以△RMQ≌△EMO(AAS),QM=OM.

因为NQ=NO,所以NM⊥OQ.

因此可证得等腰Rt△OMN,从而证得△NSM≌△MEO(AAS).

所以NS=EM=4,MS=OE=2.因此N(-6,2).

点评：作为一道几何压轴题,如何添加辅助线是学生思维的难点,突破口在于利用45°做文章,构造特殊的直角三角形,把角度关系转化长度关系.

5 多角度找到解题切入点

5.1 视角1 过M作ON的垂线得等腰直角三角形

解法2：如图5,过点M作MH⊥ON于H，过点H作HG⊥y轴于G,过点H作HF⊥ME于F,过点N作ND⊥EM延长线于D.

图5

因为∠MHO=90°,∠MOH=45°,

所以△MHO为等腰直角三角形,则HM=HO.

易证 △MHF≌△OHG(AAS),所以HF=HG,

所以

∠HEP=∠HEO=45°.

又因为PE=EO,所以HE垂直平分PO.

所以HO=HP=HM,于是MF=FP=1,则H(-3,1).

因为∠ONP+∠MON=∠OMP+∠NPM,

所以

∠ONP=∠OMP.

因为 ∠HMO+∠OMP=∠HPA+∠APM,

所以

∠OMP=∠ONP=∠HPA.

所以

HM=HP=HN=HO.

因为∠MHN=90°,所以△MHN是等腰直角三角形,易证△MDN≌△MEO.

所以DN=ME=4,DM=OE=2,则N(-6,2).

点评：利用基本图形得到角度相等进而转化为边相等,再得到等腰直角三角形,难点在于证等腰直角三角形.

解法3(面积法):如图6,过点M作MH⊥ON于H，过点H作HG⊥y轴于G,过点M作MT⊥GH延长线于T，过点N作NC⊥x轴于C.

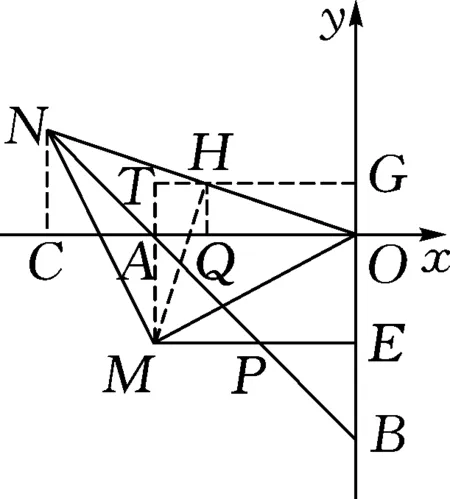
图6

易证△MHO是等腰直角三角形,△HOG≌△MHT,所以MT=HG,HT=OG.

因为四边形MEGT是矩形,所以T,A,M三点共线,AT=OG=TH.

则TG=TH+HG=TH+TA+AM,

所以AT=OG=1，H(-3,1).

因为S△OCN=S△OHQ+S四边形CQHN,设NC=AC=a,

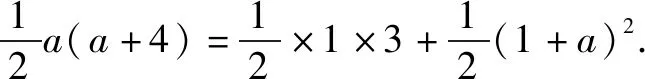
解得a=2.因此N(-6,2).

点评：利用图形面积的两种计算方法建立方程,极为简便.

5.2 视角2 过N作ON的垂线得等腰直角三角形

解法4：如图7,过点N作NC⊥ON交OM延长线于C，过点N作NG⊥AN交x轴于G,连CG交EM延长线于点D，过点N作NH⊥x轴于H.

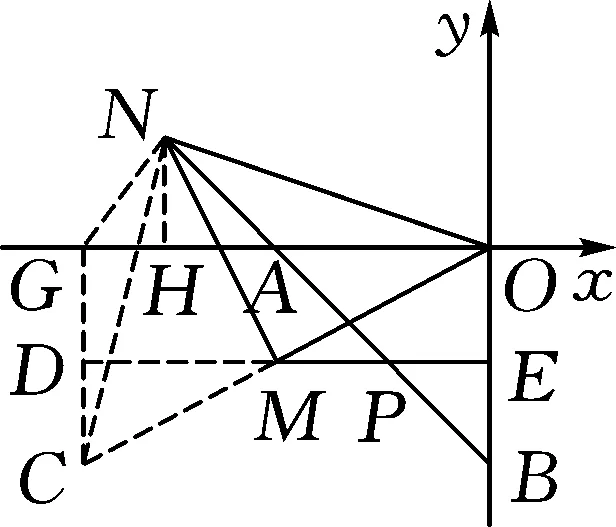
图7

易证△CNO、△ANG是等腰直角三角形.

所以∠CNG=∠ONA,从而△OAN≌△CGN(SAS).

于是AO=CG=4,∠OAN=∠CGN=135°.

因为∠AGN=45°,所以∠AGC=90°,即CG⊥OA.

于是四边形DEOG是矩形,CD=DG=2.

所以△OME≌△CMD(AAS),DM=ME=4.

所以AG=DM=4,AH=HG=2,则N(-6,2).

解法5：如图8,作NK⊥NO交OM的延长线于K,作NT⊥y轴于T,NQ⊥NT,KQ⊥NQ,连接BQ.易证△KNO是等腰直角三角形.

图8

因为∠NOM=45°,∠KNO=90°,

所以NK=ON.

因为∠KNO=∠TNQ=90°,

所以∠KNQ=∠TNO.

又因为∠NQK=∠NTO=90°,

所以△NQK≌△NTO(AAS),于是NQ=NT.

因为∠BNQ=∠BNT=45°,BN=BN,

所以△BNQ≌△BNT(SAS),

所以∠NQB=∠NTB=90°,所以K,Q,B共线.

因为ME∥BK,OE=EB,所以OM=MK.

设KQ=OT=a,则NQ=NT=4+a.

所以BK=a+4+a=2ME,a=2，则N(-6,2)

解法6：如图9,过点N作NK⊥NO交OM的延长线于K,作NT⊥y轴于T,NH⊥NB于H,连接BK.易证△KNO、△BNH是等腰直角三角形.

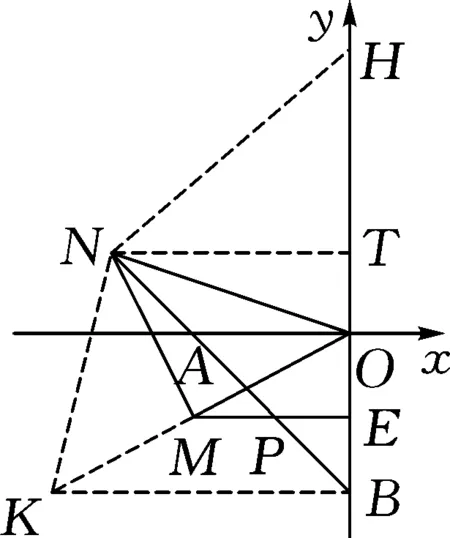
图9

因为∠KNO=∠BNH=90°,

所以∠KNB=∠HNO,

于是△BNK≌△HNO(SAS).

所以KB=OH，∠KBN=45°,因此KB⊥OB.

因为ME∥BK,OE=EB,

所以OM=MK,KB=2ME=8.

于是OH=8,BH=12,NT=BT=6,OT=2.

则N(-6,2).

点评：过点N作两条垂线,构造两个等腰直角三角形,从而得到一组全等三角形,也是常见的手拉手模型,添加的辅助线较多,用到中位线等相关知识.

5.3 视角3 过M作OM的垂线得等腰直角三角形

解法7(同一法)：如图10,过点M作MQ⊥MO交ON的延长线于Q,作QT⊥y轴于T交BA于G,QF⊥EM延长线于F.易证△QMO是等腰直角三角形,所以△MFQ≌△OEM(AAS).

图10

所以MF=2,QF=4,Q(-6,2),于是yG=yQ=2.

所以GT=TB=6,G(-6,2),则G与Q重合,

所以N与Q重合,N(-6,2).

点评：利用过一点作已知直线的垂线有且只有一条,假设有不同交点,分别计算相应点的坐标,从而判断两点重合.

5.4 视角4 挖掘隐含条件,借助相似、三角函数巧妙解决

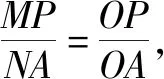
图11

因此N(-6,2).

解法10：如图12,连接OP,作MG⊥NO于G,可知OP⊥AB,∠AOP=∠NOM=45°,所以∠MOP=∠NOA.

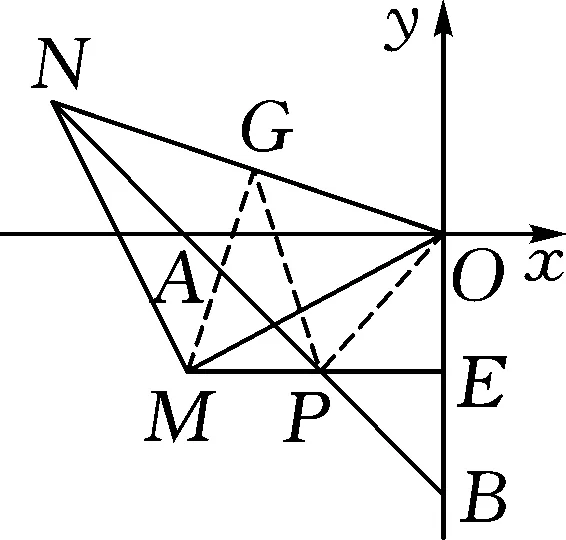
图12

因为∠NAO=∠MPO=135°,

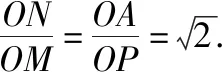
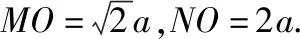
在Rt△MGO中，MG=GO=a,所以NG=a.

所以G为NO的中点.

则△NMO为等腰直角三角形,于是N(-6,2).

解法11：如图11,辅助线同解法9.设∠AOM=α,∠AON=β，α+β=45°.

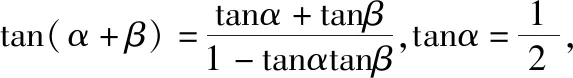
所以

设CN=CA=a,则OC=4+a,所以a=2.

则N(-6,2).

点评：利用高中三角函数的知识可以解决这道较难的压轴题,让人眼前一亮,给人一种四两拨千斤的感觉,寥寥数语就概括前面冗长的证明,体现相似、三角函数等知识力量的强大.

6 解题反思

对每道试题，命题者解答自己命制的考题时,思维往往会受到限制,给出的解答往往是单一的,甚至比较繁琐.学生对所学知识掌握的熟练程度不一致,在解答时不同的切入点往往会产生不同的解法.深化试题启迪学生思维的功能,需要教师对各种解法进行梳理,探究解决问题的一般路径和方法.

不难确定这道压轴题的难点是证明△MON是等腰直角三角形,因此构造不同的等腰直角三角形是解决本题的主要突破口,重新对知识进行组织和再加工[2],利用三垂直得到全等三角形和线段相等,进而确定点的坐标.

对已有的条件分析,可以得出一些有用的结论,如第(3)问原图上可以得到5个角都等于45°,可以证明∠OMP=∠PNO等,这些结论都是在各种解法中反复被用到的.因此,即使再复杂的数学问题都可以得到一些有用的结论,在解答复杂问题时,有必要把这些有用的结论挖掘出来,把这些隐含的辅助线连接起来.

对辅助线的添加是难点,在含45°的三角形中,有哪些构造等腰直角三角形的方法,作出垂线之后又可以连接哪些线段,这些技巧在平时的训练中需要加强练习及构建知识体系.如等腰直角三角形的性质,它的边角关系,勾股定理、一次函数、直角三角形中斜边中线的性质、一线三垂直模型等等,把这些基础知识、解题模型与本题相关的图形进行充实和重新配置,就会产生很多想法及解法.无论学生还是老师,长期坚持解题经验的积累和解题方法的思考,必然会将织牢知识网络,提升数学思维水平.

反观这道题对于初中数学解题教学的意义,可以从以下几个方面对学生直观想象素养进行培养.第一,在教学过程中注重基本图形的理解和积累.第二,让学生体会并学习数形结合的思想和方法.第三,利用多媒体教学化静为动,像几何画板、超级画板Z+Z、GeoGebra、3D数学教学平台等动态几何软件,有助于教师生动、形象地展示几何图形的各种性质和演示几何变化的动态效果,带给学生直观视觉上的冲击,有利于培养学生观察、认识周围事物间的数量关系和形体特征的兴趣和意识[3].大部分同学对于这类压轴题是望而生畏,只有教师充分认识和理解这道题的教育意义,才能在教学过程中将问题讲透彻,学生在以后遇到类似的问题时才敢于大胆尝试.