指向思维生长的数学核心概念教学实践与思考*

浙江省湖州市南浔区教育教学研究和培训中心 浙江省湖州市南浔区和孚中学 褚水林

1 引言

数学概念是思维的细胞，是数学知识的“根”，是数学认知的基础，是数学学习的内核.数学核心概念是数学概念的主体与核心，是进行判断推理的关键，在整个数学概念教学中占了主干地位，并起到了逻辑的连贯性与一致性作用，与其他基本数学概念一起，成为数学的重要组成部分.数学核心概念教学为学生的认知、核心素养培养提供了广阔的思维平台.然而，核心概念教学还未引起足够重视，未能从整体视角建构核心概念教学，轻概念的学习过程，重立竿见影的解题训练，轻概念间的联系，重单纯的模仿记忆.这样的核心概念教学，不利于学生对核心概念本质的理解，不利于学生数学思维能力的培养，不利于学生核心素养的形成.那么，在“双减”背景下如何重构核心概念教学，发挥核心概念教学的作用与价值？笔者提出指向思维成长的数学核心概念教学，让概念教学为学生知识生长、思维生长、生命成长助力，发挥核心概念课应有的育人价值.

2 诠释：指向思维生长的数学核心概念教学内涵

数学概念最重要的特征是它们都被嵌入在组织良好的概念体系中.在一个概念体系中，有些概念处于核心位置，其他概念或由它生成，或与它有密切的联系，符合上述核心概念的特征，我们称这些概念为核心数学概念[1].数学核心概念居于学科中心，是学科结构的主干部分，具有整体性、结构性、生长性等特征.基于核心概念的特征、学生的认知规律、核心素养的目标要求，数学核心概念教学重视概念的生长发展过程、学生思维的生长过程.指向思维生长的数学核心概念教学，基于数学育人价值，通过创设一定情境，以问题引领为主线，设计恰当的学习活动，学生感受学习核心概念的必要性，经历概念的形成、应用、精致过程，从而理解核心概念本质，生成概念系统，体验概念的价值，自然生长知识、方法、经验，从而不断获得思维方式和思维品质的发展，促进数学思维逐步从低阶思维向高阶思维发展，以思维生长助力学生成长，最终达到师生思维共同生长之目标.

3 实践：指向思维生长的数学核心概念教学路径

指向思维生长的数学核心概念教学，在遵循一般概念的教学基础上，还有自身的特殊要求，从工具性理解向关系性理解过渡.从整体观视角学习概念，首先需要研究“为什么学习此概念”，知道概念生成的背景和引入理由，激活学生情感需求和认知需求[2]；其次需要研究“学习概念的主要内容”，经历概念形成过程，揭示概念的本质特征，提升思维活跃度和含量；再次需要研究“学了概念有什么用”，挖掘概念学习蕴含的思想方法，知道它在建构知识或解决问题中的作用，建立相关概念之间的关系和结构体系，提升思维的联系性、深刻性.笔者以初中方程起始课(浙教版《义务教育教科书·数学》七年级上册第5章第1节“一元一次方程”)教学为例，探索思维生长的数学核心概念教学实践路径.

3.1 创设情境，引入概念

问题1：小明今年13岁，老师今年的年龄减去10岁再除以2刚好为小明的年龄，你能算出老师的年龄吗？

问题2：小明今年13岁，老师今年的年龄36岁，请问几年后小明的年龄是老师年龄的一半？

教师先引导学生回顾方程的概念，再引导学生解决问题(用算术解法或方程解法).

追问：通过比较，试说出列算式和列方程两种方法的特征？

列算式：列出的算式表示解题的计算过程,只能用已知数.对于数量关系较复杂的问题,列算式比较困难.

列方程：方程是根据题中等量关系列出的等式.已知数、未知数都可以参与运算,思维方式是顺向思维，解决问题相对比较方便.

设计意图：从师生年龄的角度入手，激发学生的求知欲，激活旧知，自然引入新知，起到先行组织者作用.本问题设计两问让学生自我评判列算式、列方程难易程度如何，第一设问列算式、列方程难易程度差不多，第二设问列方程优于列算术.通过比较，让学生初步感知和体验，逐步体会从算式到方程的进步，感受方程在解决问题过程中的重要性.

3.2 活动探究，生成概念

活动1：尝试列方程.

例1根据下列问题数量关系列方程：

问题3：2021年东京奥运会中中国运动员的表现出色，其中跳水队获得金牌7枚，是射击队获得金牌数的2倍少1.射击队获得多少枚金牌？

设射击队获得x枚金牌，可列出方程：.

问题4：小强、小杰、张明参加投篮比赛，每人投了20次.小强投进10个球，小杰比张明多投进2个，三人平均每人投进14个球.问小杰和张明各投进多少个球？

设张明投进x个，可列出方程：.

问题5：长方形的周长为28米，长比宽多3米，则长方形的长和宽分别为多少米？

①设长方形的宽为a米，则长为(a+3)米，可列出方程：；

②设长方形的宽为a米，长方形的长为b米，根据题意，可列出方程：.

问题6：长方形的面积为28平方米，长比宽多3米，长方形的长为多少米？

设长方形的长为m米，可列出方程.

设计意图：设计不同背景问题，学生经历“找等量关系，列方程”的过程，让学生体会到方程是刻画现实世界数量关系的有效模型，同时为学生自主建构一元一次方程及相关概念做准备.

活动2：识别特征，形成概念.

学生按照未知数的个数和次数分别进行分类：按未知数个数(即“元”)，可分为一元、二元；按未知数的次数，分为一次、二次.此时教师要善于引导学生发现这些方程的共性：方程的两边都是整式；特性：未知数的个数、未知数的最高次数.

你能否再举一些具有这些特征的方程的例子?

在学生归纳、概括这三个方程的本质属性基础上，引导学生尝试对一元一次方程下定义.

设计意图：从方程整体的视角，提供丰富的方程例子，学生经过观察、分析、比较再分类，逐步归纳属性.通过观察所列方程的共同特征，培养学生归纳概括能力，渗透数学抽象这一核心素养.

问题9：类比一元一次方程定义，方程④2(a+b)=28，⑤a-b=3，⑥m(m-3)=28，这三个方程分别可以称为什么方程？能否给这些方程下定义？

设计意图：类比一元一次方程定义，让学生抓住方程的“元”“次”尝试给二元一次方程、一元二次方程下定义，体现概念的生长、思维的生长.

3.3 应用迁移，理解概念

活动3：辨析概念.

(1)下列各式中，哪些是方程？哪些是一元一次方程？

①5x=0；②1+3x；③y2=4+y；④3m+2=1-m.

活动4：尝试检验，体验方法.

例2利用问题2引入一元一次方程解的尝试探究：

小明今年13岁，老师今年的年龄36岁，请问几年后小明的年龄是老师年龄的一半？

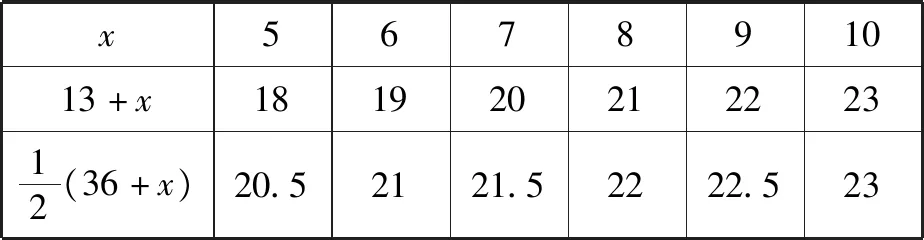
表1

设计意图：设计尝试用逼近法求方程解的活动，既让学生感受解方程的一般方法，又自然引出方程解的概念.

3.4 反思总结，构建概念系统

问题：本节课我们学习了哪些主要内容？

通过本节课的学习，你对算式和方程在解决问题中的作用有哪些新的认识？

我们通过怎样方法学习一元一次方程？

师生共同梳理归纳，形成结构图，如图1.

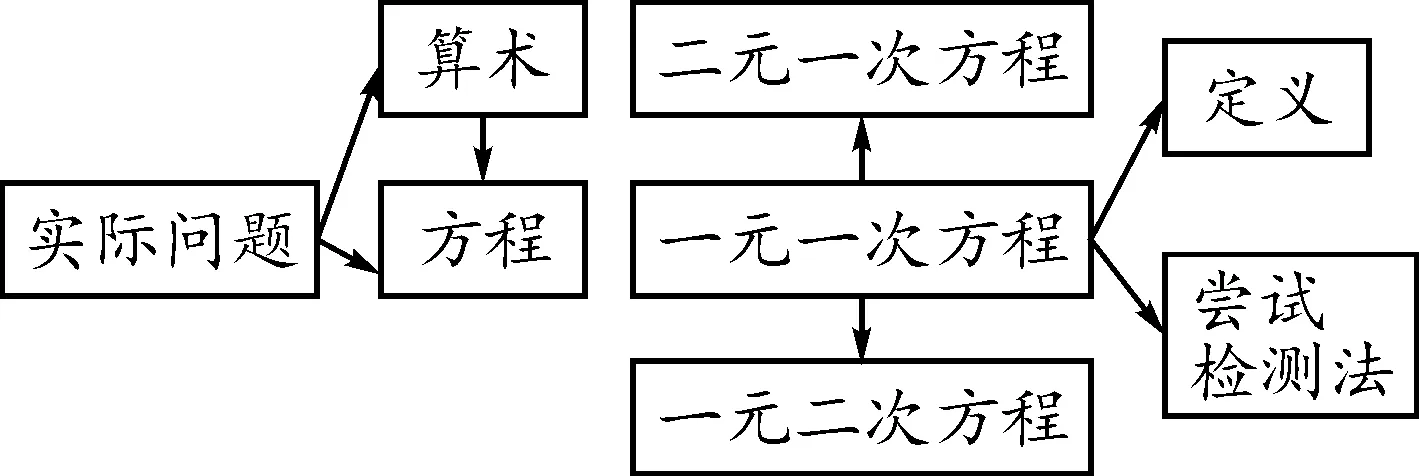
图1 一元一次方程概念结构体系网络图

设计意图：设计问题串引导学生梳理总结所学知识、方法并以思维导图形式呈现，使之形象化、结构化、网络化，促进对新概念的深度理解和深度思维.

4 反思：指向思维生长的数学核心概念教学启示

4.1 理解教材，把握数学核心概念本质

思维生长的数学核心概念课，关键在于深度理解核心概念、迁移应用概念并能建构概念体系.教师在教学设计时需要整体解读教材，明白教材的编写意图，并对不同版本的教材进行精选和整合.

初中阶段方程起始课不同教科书课题名称不尽相同，如人教版的课题“从算术到方程”，浙教版的课题“一元一次方程”，不同的课题意味目标立意也有所侧重.方程起始课教学从整体观、系统观的思维创造性地用教材，本课例在浙教版提供的学习素材基础上，增加了算术解法与方程解法比较的内容，让学生体会到从算式到方程的进步；在列方程时增加了不同类型的整式方程，通过对列出方程的分类逐步获得一元一次方程的概念，在此基础上生长二元一次方程、一元二次方程，体现了低起点、高立意，体会方程的价值和方程思想，体验到核心概念的生长过程.

4.2 创设情境，感受学习核心概念的必要性

核心概念教学不仅要知其然，而且知其所以然.通过解决现实问题需要的分析，让学生感受数学与现实的联系，产生核心概念学习的情感需求；通过数学自身发展的分析，让学生产生数学核心概念学习的思维需求.通过问题1、问题2师生年龄问题情境，采用“一题多解”的方式，让学生感受算术法与方程法的区别，初步体会方程法的优越性，逐步实现从算术法到方程法的思维转换，体会方程思想.

4.3 设计活动，经历核心概念的形成过程

史宁中教授指出，抽象是从许多事物中舍弃个别的、非本质属性，得到共同的、本质属性的思维过程，是形成概念的必要手段[3].数学概念的形成往往是从具体到抽象、从特殊到一般的过程，数学核心概念学习成为发展学生数学抽象能力的重要载体.因此，数学核心概念尽量以“概念形成”的方式学习，使学生真正经历辨别—分化—抽象—概括—表示等思维活动过程.在一元一次方程的概念形成教学中，通过列方程、给所列方程分类、再聚焦到一元一次方程的共同属性归纳抽象，从整体到局部，从共性到特性，从整式方程到一元一次方程，类比一元一次方程对二元一次方程、一元二次方程初步认知，体现方程的整体性，体现数学概念的自然形成过程、生长过程.

4.4 搭建支架，促进数学思维的自然生长

核心概念教学追求的是思维的自然生长，追求思维动力、思维品质、思维能力得到自然、必然生长.一是营造环境，激发学生思维动力.需要产生的一种心理反应就是动机，学生的需要，就是激发学生思维动机的出发点.教学中立足学生的认知起点、思维起点、情感需求，营造和谐的师生关系，从而产生思维的动机，增强激发思维的内驱力.二是设计问题链，引发学生思考，提升思维品质.本案例通过问题1、问题2，引发学生对算术方法与方程方法比较，让学生感受到学习方程的必然性；通过问题3～6的设计，让学生经历列方程的过程，感受方程是刻画现实世界数量关系的一种模型，初步形成建立方程模型解决问题的意识；通过问题7～9，逐步归纳一元一次方程的本质属性，发展学生的抽象概括能力；通过问题2引导学生首次经历一元一次方程解的尝试探究，方程解的概念、尝试检验解融合在一起，学生的创新思维、深度思维得到培养.三是思维导图，形成思维结构化.核心概念教学注重概念间的联系，以思维导图建构概念认知结构网络，以此促进概念本质理解，促进学生深度思维、结构化思维.

教育的出发点与落脚点就是让学生全面发展、健康成长.指向思维生长的核心概念教学，要站在学生的生命视角，重构核心概念教学结构，以“内容问题化、问题活动化、活动思维化”为关键要素，让学生感受学习核心概念的必要性，经历核心概念的形成、应用过程，让学生养成从核心概念出发思考问题、解决问题的习惯，让学生学会从概念的联系中创新思维，关注数学本质，让概念教学为学生知识生长、思维生长、生命成长赋能，发挥核心概念课育人价值.