预应力型钢混凝土梁-角钢混凝土柱框架节点核心区受剪承载力研究

王 琨，时金雨，徐冠普，顾明君

(1.扬州大学建筑科学与工程学院，江苏 扬州 225127；2.江苏邗建集团有限公司，江苏 扬州 225127)

预应力型钢混凝土梁结合了型钢混凝土梁与预应力混凝土梁的优点，如较高的承载力、刚度及良好的抗震性能，目前已在大跨和重荷等结构中得到了广泛的应用[1-5]。角钢混凝土柱是将普通钢筋混凝土柱中的钢筋替代为角钢、箍筋替代为钢板箍所形成的一种空腹式型钢混凝土构件，与普通钢筋混凝土柱相比，具有更高的承载力和延性[6-8]。在此基础上形成的预应力型钢混凝土梁-角钢混凝土柱框架结构也表现出优良的抗震性能，已应用于既有房屋的套建增层改造中[9-12]。

在前期工作中，本课题组开展了型钢混凝土梁-角钢混凝土柱框架边节点的有限元数值模拟，探讨了此类节点的受剪性能[13]。在此基础上，完成了预应力型钢混凝土梁-角钢混凝土柱框架中节点的滞回性能试验[14]，研究了不同预应力度和轴压比下节点的抗震性能。目前，有关预应力型钢混凝土梁-角钢混凝土柱框架节点的设计方法目前还鲜有报道。然而，由于预应力对节点核心区抗剪承载力的提高可能受到角钢的影响，同时角钢和钢板箍对节点核心区的约束作用也不明确，节点内钢梁腹板屈服范围亦难以界定。因此，笔者在试验基础上，建立了预应力型钢混凝土梁-角钢混凝土柱框架节点的有限元模型，并开展参数分析，揭示了预应力度、轴压比、型钢腹板厚度、钢板配箍率及角钢配钢率对节点水平荷载-位移曲线和核心区剪力-剪切变形的影响，提出了基于型钢腹板、钢板箍、预应力筋和混凝土贡献的核心区抗剪承载力计算公式。研究表明，节点核心区的抗剪承载力计算公式计算结果与试验值吻合较好，可为我国在实际工程中推广应用此类框架结构和相关规范修订提供基础资料和技术支撑。

1 试验概况

笔者制作了3个预应力型钢混凝土梁-角钢混凝土柱组合节点(编号分别为SJ-1、SJ-2、SJ-3)以及1个非预应力型钢混凝土梁-角钢混凝土柱组合节点(编号为SJ-4)。4个试件轴压比分别为0.15、0.31、0.15、0.15，构造配筋如图1所示。为便于理论分析，预应力筋直线布置。所有试件混凝土均采用C40，实测混凝土立方体抗压强度为46.8 MPa；节点试件内型钢采用I22a，型钢锚脚采用I10a，加劲肋采用厚7.5mm钢板，屈服强度分别为289.3 MPa、282.1 MPa、344.0 MPa；梁内纵筋分别采用8和12，屈服强度分别为394.9 MPa和399.2 MPa；梁内箍筋采用8，屈服强度为388.4 MPa；柱内角钢和钢板箍的屈服强度分别为306.9 MPa和295.8 MPa；实测预应力筋φs12.7和φs15.2的抗拉强度分别为1 710.0 MPa和1 940.0 MPa。试验中，水平低周往复荷载施加于柱顶，柱底与刚性地梁铰接，梁端设置可产生水平侧移的可动铰支座。

图1 试件构造及配筋Fig.1Reinforcement of specimen structure

2 有限元模型的验证

2.1 材料本构关系

梁柱内箍筋和钢板箍将分别对受压混凝土产生约束作用。在模拟中将钢板箍视作同等面积的钢筋，同时忽略工字钢对梁核心区混凝土的约束作用，则预应力型钢混凝土梁和角钢混凝土柱截面混凝土可划分为保护层和箍筋(钢板箍)约束区两个部分(见图2)。对预应力型钢混凝土梁内箍筋约束区混凝土、角钢混凝土柱内钢板箍约束区混凝土的受压应力-应变关系采用文献[15]中的约束混凝土模型；梁柱保护层混凝土的受压本构关系以及所有混凝土受拉本构关系均采用《混凝土结构设计规范》(GB50010—2010)[16]提供的双参数本构模型；纵筋、箍筋、工字钢、角钢以及钢板箍均采用理想弹塑性本构模型；预应力筋本构关系采用三折线模型[17]。

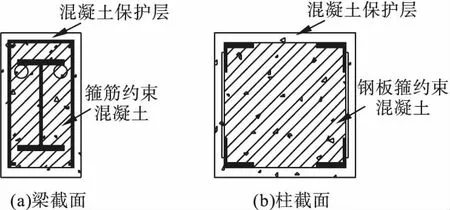
图2 混凝土截面划分Fig.2Concrete section division

2.2 单元类型与荷载施加

预应力型钢混凝土梁-角钢混凝土柱节点试件有限元模型见图3。混凝土采用实体单元，钢管和工字钢采用壳单元，纵筋、箍筋和预应力筋均采用三维桁架单元。混凝土网格尺寸控制在80 mm以内，型钢网格控制在35 mm以内。建模过程中不考虑钢筋、型钢、钢板箍等与混凝土之间粘结滑移影响因素，其与混凝土之间的相互作用均采用Embedded region定义，非预应力框架节点类似。有限元模型采用位移加载方式。

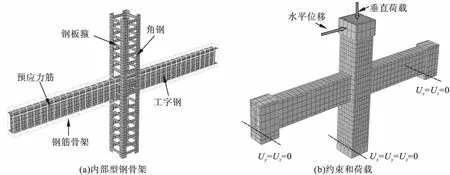
图3 节点试件有限元模型Fig.3Finite element models of joint specimens

2.3 结果分析

根据有限元数值模型，分析模拟得到SJ-1～SJ-4在柱顶水平荷载作用下的荷载-位移(P-Δ)曲线，并与试验滞回曲线进行对比，结果如图4所示。由图可知，模拟曲线的初始刚度与试验结果相比略大，水平峰值荷载与试验结果较为一致。

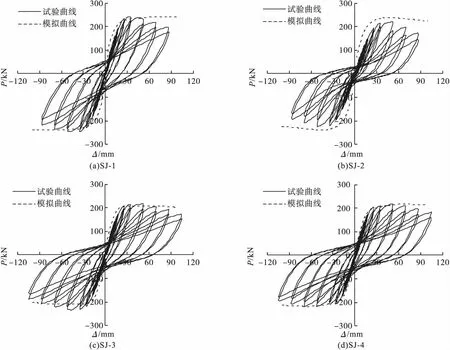
图4 荷载-位移曲线对比结果Fig.4Comparison of calculation curves and test curves

以试件SJ-1为例，图5给出了当水平荷载下降为峰值荷载的85%时，计算得到的节点核心区和周边范围混凝土主压应变分布以及节点试件的实际破坏形态。

图5 混凝土主压应变分布及破坏形态Fig.5Principle compressive strain and failure mode of concrete

通过图5(a)可知，在达到极限状态时，梁端受压区有小范围的混凝土超过了极限压应变，表明梁端发生了一定程度的弯曲破坏，同时节点核心区混凝土也已形成了范围较宽且呈45°的非常明显的斜压杆，其压应变超过了极限压应变，表明节点核心区混凝土最终发生了剪切破坏。

不同阶段的内部型钢骨架Mises应力分布如图6所示。从图中可以看出，试件屈服时，角钢骨架范围的工字钢腹板大部分区域达到了屈服强度，同时节点域钢板箍也已屈服；荷载达到峰值时，角钢骨架范围内的工字钢腹板和钢板箍均达到了屈服，而此时角钢未出现屈服，梁端型钢翼缘屈服，表明梁端也形成了明显的塑性铰；在达到破坏荷载时，节点核心区工字钢腹板屈服区域进一步扩展，并向节点域外延伸，与梁端部工字钢腹板的屈服区域相连。

图6 不同阶段型钢骨架应力分布Fig.6Stress distribution of embedded steel at different stages

3 节点受剪承载力

3.1 节点核心区剪力与剪切变形计算方法

节点试件和其核心区域受力如图7所示，不考虑二阶效应的影响。

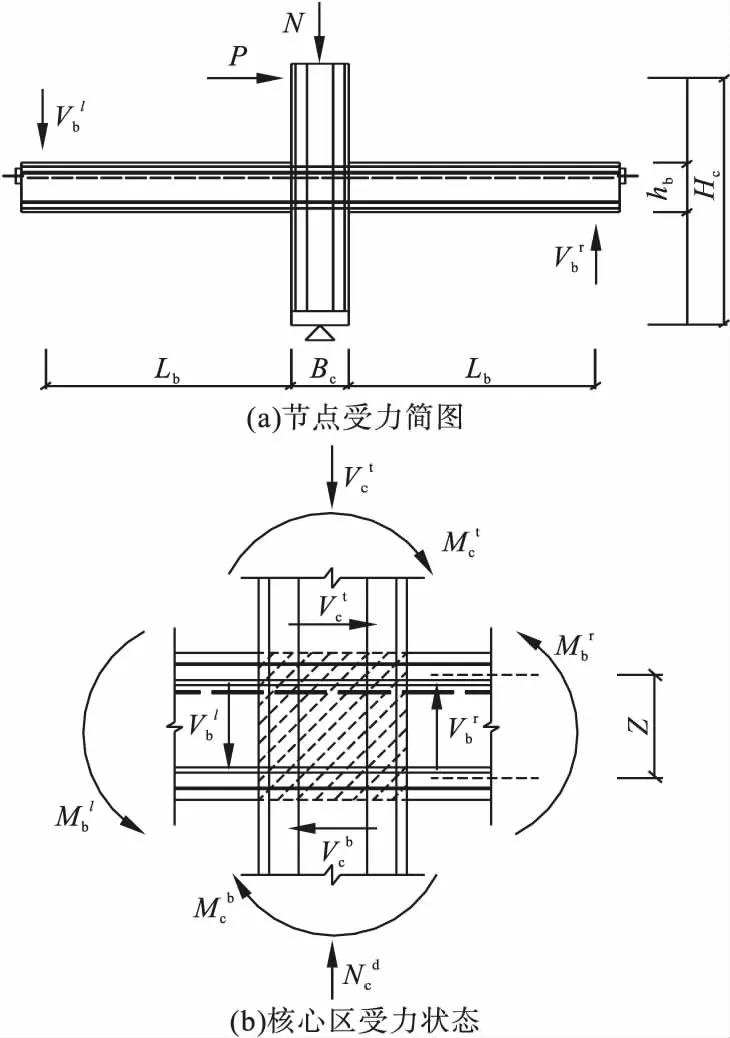
图7 节点剪力计算示意图Fig.7Joint shear calculation diagram

根据图7(a)可得力矩平衡方程 (1)，将式 (1)代入式节点核心区剪力计算式 (2)中，可求得节点核心区剪力Vj。图7中，P为柱顶水平荷载；N为柱顶竖向荷载；Mbl、Mbr分别为左右梁端弯矩；Mct、Mcb分别为上下柱端弯矩；Vbl、Vbr分别为左右梁端剪力；Vct、Vcb分别为上下柱端剪力；Nct、Ncb分别为上下柱端轴力；Hc为上下柱反弯点间的高度；Z为梁端截面拉、压合力点之间的距离；hb为梁截面高度。

(1)

(2)

受剪力作用时，节点核心区将由矩形转变为菱形(见图8)，可按式(3)计算核心区的剪切变形：

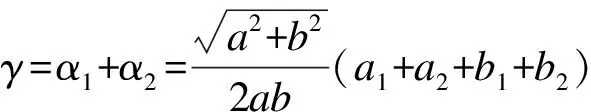
(3)

式中：γ为试件核心区的剪切角；α1、α2分别为变形后的菱形边与原矩形边的夹角；a1、a2、b1、b2分别为核心区对角线上的缩短和伸长量。

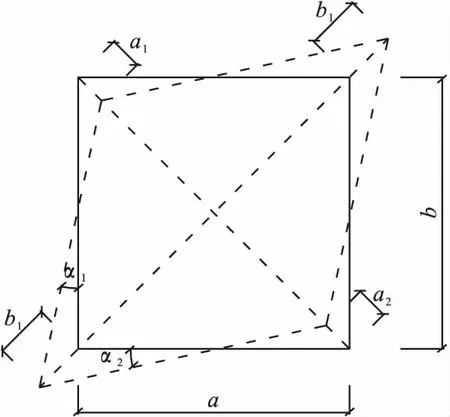
图8 节点核心区变形Fig.8Shear deformation of panel zone

3.2 参数分析

为研究预应力度λ、轴压比n0、型钢腹板厚度tw、核心区配箍率ρsv以及柱角钢配钢率ρa等参数对试件中节点核心区受剪承载性能的影响，进行有限元模型分析。其中预应力度λ分别为0、0.4、0.48，采用的预应力筋为2ϕs12.7和2ϕs15.2；轴压比n0分别为0.1、0.3、0.5、0.7、0.9；型钢腹板厚度tw分别为5 mm、7.5 mm、10 mm；核心区配箍率ρsv分别为1.96%、2.45%、2.94%，对应的钢板箍厚度为4 mm、5 mm、6mm；柱角钢配钢率ρa分别为2.59%、3.45%、4.31%，对应的角钢分别为L70×6、L70×8、L70×10。

不同参数下荷载-位移(P-Δ)曲线及剪力-剪切角(Vj-γj)曲线见图9～图13。

图9 预应力度的影响Fig.9Influence of prestressing level

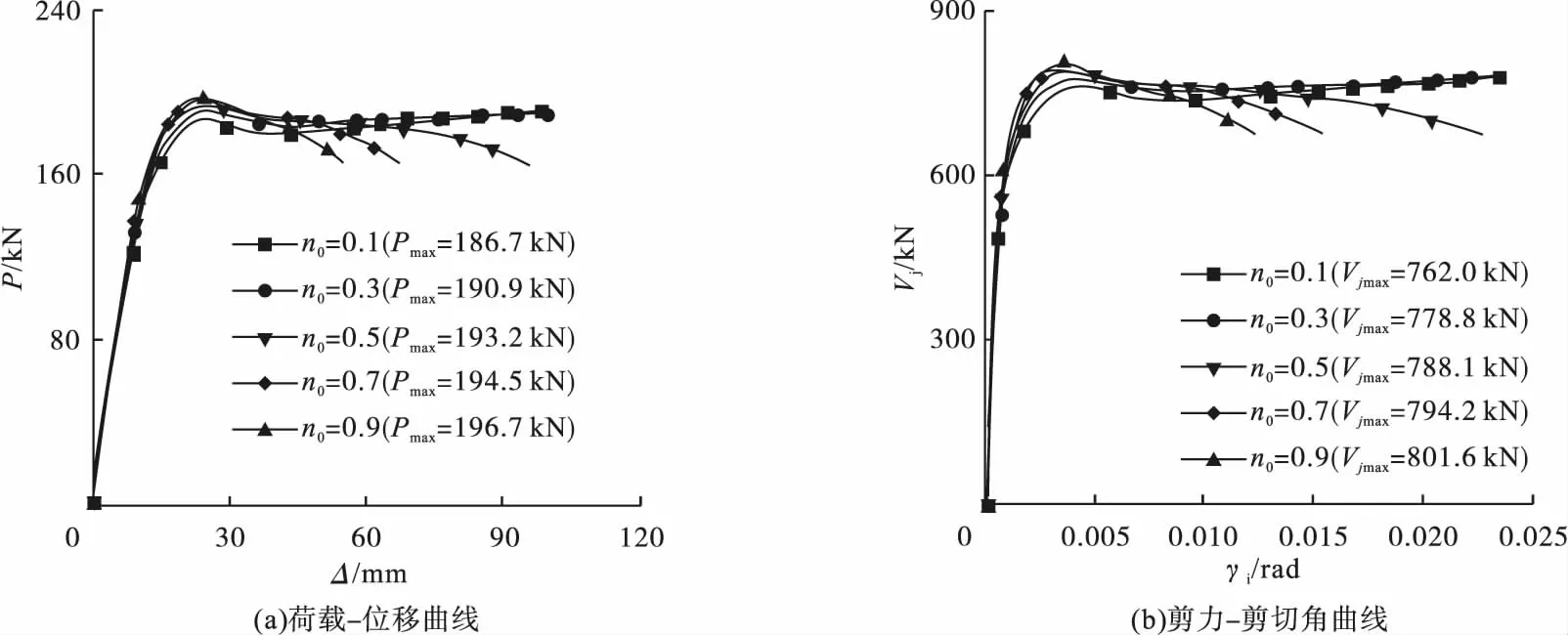
图10 轴压比的影响Fig.10Influence of axial compression ratio

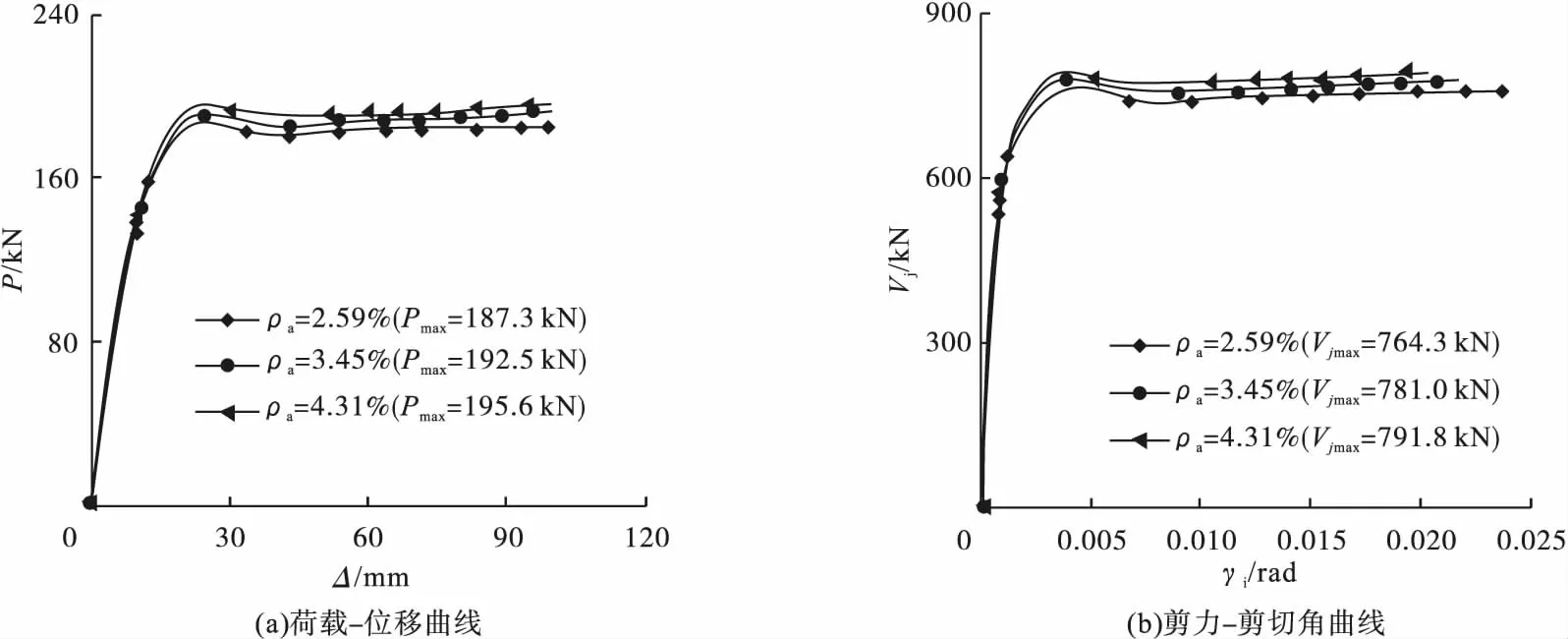
图11 角钢配钢率的影响Fig.11Influence of angle-steel ratio

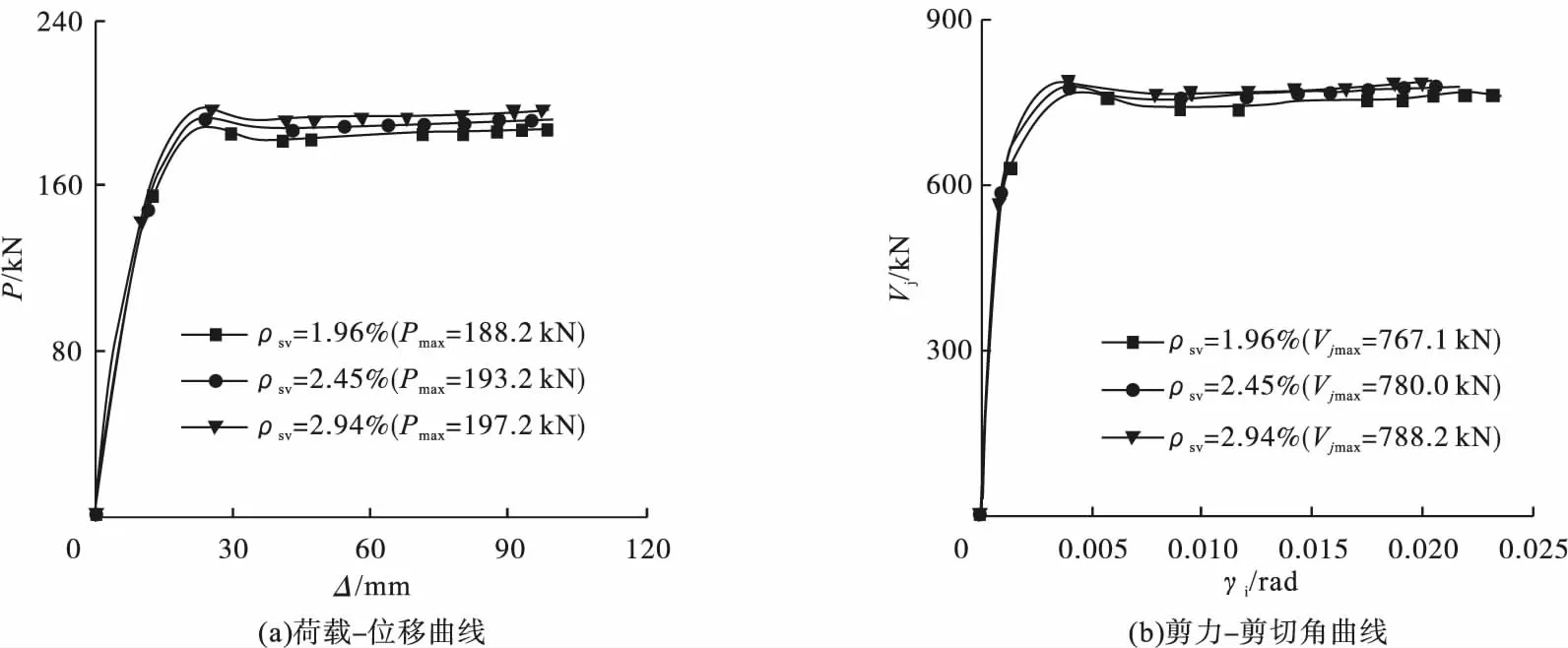
图12 核心区配箍率的影响Fig.12Influence of stirrup ratio in panel zone

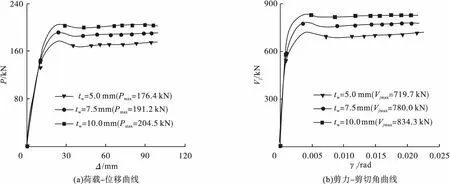
图13 工字钢腹板厚度的影响Fig.13Influence of thickness of I-shaped steel

从图9可以看出，随着预应力度的增加，水平荷载和节点核心区抗剪承载力均随着预应力度的增加而增大。从图10可以看出，随着轴压比的增大，节点试件的柱端水平荷载和核心区剪力随之增大，但当轴压比超过0.5时，轴压比的增大对提高节点核心区的受剪承载力影响较小，且轴压比越大，曲线的下降段刚度也会随之增加，表明节点试件的延性在不断降低。从图11可知，随着角钢配钢率ρa的提高，角钢的销栓作用增强，节点的抗剪承载力得到相应的提高。从图12和图13可以看出，随着核心区配箍率ρsv以及型钢腹板厚度tw的增加，节点试件的柱顶水平荷载增大，节点核心区受剪承载力也得到了提高；其中型钢腹板厚度的增加可显著提高节点的受剪承载力。

3.3 节点受剪承载力计算

根据前述受力分析，结合各参数对核心区剪力-剪切变形曲线可以看出，节点核心区的受剪承载力主要由型钢腹板、钢板箍、预应力筋和混凝土四个部分提供，这里暂不考虑型钢翼缘与型钢锚脚的抗剪作用。

通过前述有限元分析可知，角钢骨架范围内的型钢腹板均达到了屈服强度，因此型钢腹板提供的抗剪承载力Vss可按式(4)计算：

Vss=0.58fssAss.

(4)

式中：fss为型钢屈服强度；Ass为角钢骨架范围内的型钢腹板截面面积。

钢板箍在试验及有限元分析中均达到了屈服，则钢板箍提供的抗剪承载力Vsv可由 (5) 确定：

(5)

式中：fyv为钢板箍屈服强度；Asv为钢板箍截面面积；hb0为节点核心区截面有效高度；a′s为受压角钢至受压混凝土边缘的距离。

经参数分析可知，预应力筋提供的抗剪承载力Vp可按下式计算：

Vp=0.314Np+1 543ρa-49.95.

(6)

为偏于安全，对预应力筋提供的抗剪承载力取参数分析结果的下限，则Vp可按下式计算：

Vp=0.2Np.

(7)

经拟合可得混凝土提供的抗剪承载力Vc：

Vc=(0.23+0.8ρa+0.02n0)fcbjhj.

(8)

式中：bj和hj分别为节点核心区截面宽度和截面高度。

经过上述分析，可得到节点核心区受剪承载力Vu的计算公式：

Vu=Vc+Vss+Vs+Vp=

(0.23+0.8ρa+0.02n0)fcbjhj+0.58fssAss+

(9)

4个节点试件(包含非预应力试件)的抗剪承载力试验值Vut和按式(9)计算得到的抗剪承载力Vuc结果见表1。从表中可以看出，Vut和Vuc相差较小，两者比值的均值为1.01，标准差为0.045，分别小于1.05和0.05。表明此式(9)可用于此类节点抗剪承载力的设计计算。

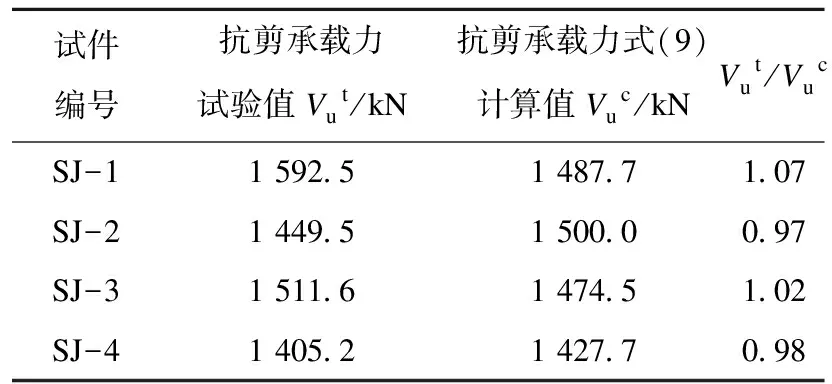
表1 抗剪承载力比较Table 1Comparison of tested and calculated shear forces

4 结 论

(1)通过合理地选择材料本构关系和单元类型，建立的有限元数值模型可对试件开展全过程分析，计算结果与试验结果吻合较好。

(2)提高预应力度、角钢配钢率和型钢腹板厚度以及配箍率均可一定程度提高节点核心区的受剪承载力，其中腹板的厚度对抗剪承载力影响最明显；随着轴压比的增加，节点的抗剪承载力增加并不显著，但水平峰值荷载对应的位移在减小，下降段延性在降低。

(3)建立了节点核心区的抗剪承载力计算公式，并与试验结果进行了对比，两者吻合较好，可为工程设计提供参考。