双肢梯形冷弯薄钢格构柱轴压承载力研究

金 路，钱晶晶，徐 冬，张飞扬，陈 强

(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168；2.中建二局第四建筑工程有限公司，天津 300457)

冷弯薄钢具有质量轻、强度高、运输方便、绿色经济等优点，常用于低层轻型房屋中梁柱承重构件[1-3]。随着轻型钢结构的广泛需求和涌现，常见的C形、U形、Z形等单肢或拼合实腹式冷弯薄壁柱不足以满足结构设计和使用功能要求。相比实腹柱，格构柱具有材料分布合理、易满足等稳定性要求、构件抗扭性能和抗弯性能优异、工业化程度高等优点，现已被广泛应用于工业厂房、大跨度房屋、塔桅结构、海洋平台结构等体系。因此研究冷弯薄钢格构柱的承载性能和屈曲性能，提出相关设计方法和完善我国冷弯薄钢设计规范尤为重要。

现行北美AISI规范[4-6]针对单肢和双肢拼合冷弯薄壁型钢构件提出了设计方法；我国《低层冷弯薄壁型钢房屋建筑技术规程》(JGJ227—2011)[7]对多肢拼合截面柱的轴压承载力计算提出了单肢立柱轴压承载力叠加方法。虽然国内外学者对于单肢或拼合的实腹式冷弯薄壁构件受力性能已有较为系统的研究[8-9]，但针对格构式冷弯薄钢构件的承载性能和整体稳定性能的研究较少，尚缺乏安全可靠的设计方法和相关规定。M.A.DAR等[10]对缀条式冷弯型钢拼合柱的试验研究表明缀条长细比、布置形式和端板宽度对CFS拼合柱的受力性能影响显著；A.P.BONAB等[11]通过数值模拟发现肢件的长细比和缀件截面形状可影响格构柱抗震性能；詹齐涛等[12]研究了轴心受压格构方柱的受力变化规律和影响因素，为格构式冷弯薄钢压杆的设计提供依据。

基于上述分析，笔者提出一种缀条式双肢梯形冷弯薄钢格构柱，采用有限元分析软件ABAQUS模拟构件在轴向荷载作用下的力学性能，分析其应力发展趋势和破坏机理;研究柱高和腹板高度参数变化对薄钢格构柱极限承载力的影响机制，并选用有效宽度法对构件进行轴压极限承载力计算，为双肢冷弯薄钢格构柱承载力计算及构件设计提供依据。

1 有限元模型

1.1 几何参数

一种缀条式双肢梯形冷弯薄钢格构柱具体截面形式如图1所示。该构件分肢为长卷边直角梯形，梯形截面上下翼缘尺寸可灵活布置，通过改变卷边长度调整截面绕虚轴的惯性矩，使得构件尽可能满足轴压荷载作用下等稳定性要求，同时提高构件的双向抗弯性能。

经试算，共设计5种格构柱高度L：900 mm、1 500 mm、2 100 mm、2 700 mm、3 300 mm和4种薄钢格构柱腹板高度hw：80 mm、100 mm、120 mm、140 mm的20种工况，构件其他几何尺寸详见图1。缀条长×宽×厚为212 mm×30 mm×2 mm。工况编号以TC900-80为例，代表梯形截面格构柱柱长为900 mm、腹板高度为80 mm。

图1 缀条式梯形冷弯薄钢格构柱截面形式Fig.1Section form of laced cold formed thin steel trapezoid lattice column

1.2 模型的建立

通过有限元分析软件ABAQUS建立双肢梯形冷弯薄钢格构柱模型，进行轴压性能全过程数值分析。采用Shell S4R壳单元模拟格构柱和缀条；构件选取Q235钢材，钢材本构关系采用双线性强化弹塑性力学模型(见图2)。其中，屈服强度fy=235 MPa，εy为屈服应变，弹性模量E=2.06×105MPa，泊松比v=0.3，切线模量Et取0.03E。

图2 钢材本构关系Fig.2Constitutive relation of steel

双肢梯形冷弯薄钢格构柱缀条斜45°角连接构件两侧翼缘，缀条与分肢构件接触面选用绑定约束模拟二者连接。薄钢格构柱头和柱脚分别建立截面几何中心点，并将顶面和底面的六个自由度与几何中心点耦合。薄钢格构柱采用两端铰接约束。经试算网格尺寸划分为10 mm×10 mm为宜，有限元模型如图3所示。

图3 有限元模型Fig.3Finite element model

1.3 有限元模型验证

笔者选取文献[10]中四肢冷弯薄钢格构柱的轴压试件SL-150-75-60-1705进行有限元模型对比验证。试验破坏结果与有限元破坏结果如图4所示。有限元破坏结果与试验破坏模式基本一致，均为缀条连接处局压破坏。通过有限元计算得到的极限承载力为118.1 kN，试件极限承载力为121.0 kN，二者相差5%以内，且荷载-位移曲线吻合较好。由此证明文中有限元模型可靠合理。

图4 模型验证结果Fig.4Model validation results

2 初始几何缺陷

对5组双肢梯形冷弯薄钢格构柱进行特征值屈曲分析，提取前四阶模态，分析结果作为薄钢格构柱非线性屈曲分析的依据。以TC900系列为例，构件第一阶特征值屈曲模态如图5所示。由图可知，第一阶屈曲均发生在跨中腹板处。

图5 TC900柱第一阶特征值屈曲模态Fig.5The first-order eigenvalue buckling mode of TC900 columns

由于冷弯薄钢构件残余应力对其极限承载力影响可忽略不计[13]，因此笔者只考虑初始几何缺陷的非线性影响。初始几何缺陷以第一阶特征值屈曲模态施加，整体弯曲模态的比例因子取L/1 000，其中L为构件长度；截面局部屈曲模态的比例因子取0.005 5hw，其中hw为腹板高度[14]。

3 数值分析

3.1 应力分析

通过ABAQUS有限元模拟分析得到不同柱高及腹板高度变化下双肢梯形冷弯薄钢格构柱的轴压性能，得到各工况模型的应力迁移过程、极限承载力、刚度变化及破坏形态，以TC900、TC2100、TC3300系列构件为例，破坏时刻应力云图详见图6～图8所示。

由图6可知，TC-900柱主要破坏模式为局压强度破坏。加载初期P≤45 kN时，构件整体应力分布均匀，随着轴压荷载持续增大，最大应力首先出现于跨中腹板处，且应力集中严重；当荷载达到P=100 kN时，构件TC900-80和构件TC900-120均在跨中出现全截面应力集中，构件TC900-140腹板局部屈曲愈加明显，并伴有斜卷边畸变屈曲现象(见图6(d))；所有构件均从分肢跨中腹板处局压破坏导致全截面屈服而发生破坏。

图6 TC900系列破坏时刻应力分布云图Fig.6Stress distribution diagram of TC900 series at failure time

由图7可知，TC-2100系列构件在加载初期，构件整体受力均匀，最大应力首先发生在格构柱分肢较宽翼缘处；随着腹板高度的增加，构件绕实轴抗弯刚度逐渐加大，破坏模式由绕实轴整体失稳转为局压破坏，两缀条间腹板及翼缘处出现局部屈曲，呈半波屈曲模式，随后最大应力发生在跨中截面，接着全截面屈服，整个构件逐渐丧失承载能力。

图7 TC2100系列破坏时刻应力分布云图Fig.7Stress distribution diagram of TC2100 series at failure time

图8 TC3300系列破坏时刻应力分布云图Fig.8Stress distribution cloud diagram of TC3300 series at failure time

由图8可知，TC-3300系列主要发生整体失稳破坏。构件TC3300-80一侧翼缘应力持续增大，而另一侧变化较小，随着构件整体弯曲，在跨中处应力集中现象明显，截面内应力逐渐由翼缘迁移到相邻腹板处，此时轴压承载力达到最大Pmax=61.89 kN。而当腹板高度hw≥120 mm时，在加载上升阶段，构件整体受力均匀；荷载持续增加，腹板处应力逐渐增大，构件内最大应力由整个截面迅速迁移到单肢截面内，最后绕虚轴发生失稳破坏。且随着腹板高度增加，柱跨中侧向位移明显降低，说明增大腹板高度能有效提高构件抗弯刚度，减小构件变形。

3.2 柱高影响

图9为不同柱高构件的荷载-位移曲线，图10为柱高对构件承载力的影响曲线。

图9 不同柱高构件荷载-轴向位移曲线Fig.9Load-axial displacement curves of different column height

图10 柱高对构件承载力的影响

对比构件TC900-80、TC1500-80、TC2100-80、TC3300-80，极限承载力从108.65 kN下降至61.89 kN，Pmax降幅依次为1.71%、8.95%、25.48%、43.04%；对比构件TC900-100、TC1500-100、TC2100-100 、TC3300-100，极限承载力从126.08 kN下降至86.96 kN，Pmax降幅依次为2.81%、7.17%、15.08%、31.03%。综上，柱高对构件轴压极限承载力影响显著，随着格构柱柱高增加，相同截面构件轴压极限承载能力均有下降，且下降趋势由缓转快。

3.3 分肢截面腹板高度影响

选取TC900、TC2100、TC3300系列柱荷载-位移曲线如图11所示，截面腹板高度对构件承载力的影响曲线如图12所示。

图11 不同腹板高度荷载-轴向位移曲线Fig.11Load - axial displacement curves of different web height

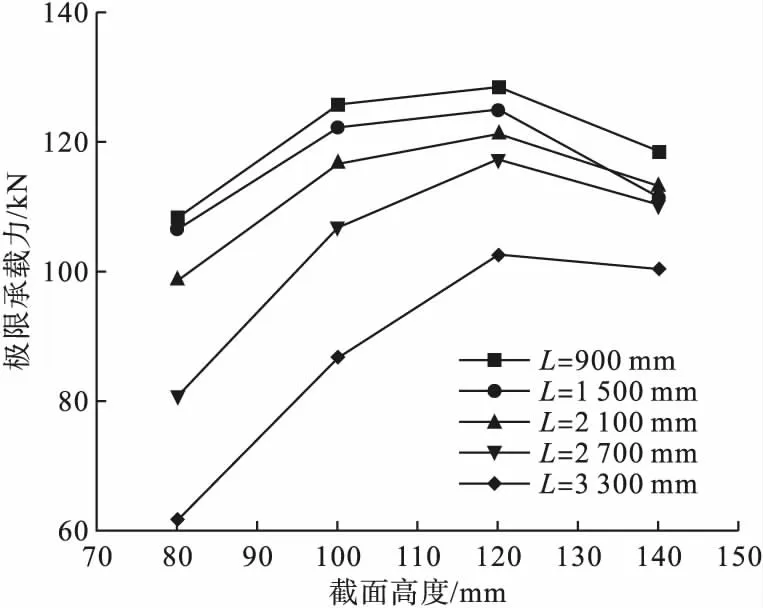
图12 腹板高度对构件承载力的影响Fig.12Influence of web height on bearing capacity of members

TC900系列构件中，当腹板高度hw由80 mm增至120 mm，柱轴压承载力从108.65 kN增至128.81 kN，提高18.55%；当腹板高度hw由120 mm增至140 mm，构件承载力反而降至118.83 kN，降低7.75%。在TC2100系列中，随着腹板高度增加，承载力变化规律与TC900系列一致，均表现为先增大后降低，且总体变化幅度较小。其中构件TC2100-120相比构件TC2100-80承载力提高22.83%，构件TC2100-140相比TC2100-120承载力降低7.04%。而TC3300系列构件当腹板高度hw由80 mm增至140 mm，柱轴压承载力持续增长，极限承载力Pmax由61.89 kN增至102.83 kN，提高66.15%。

由图12可知，随着腹板高度增加，构件承载力随之提高，且hw=120 mm时柱极限承载力达到最大，但过大的腹板高厚比导致局部屈曲极限承载力下降，如腹板高度hw=140 mm此类柱。综上，当格构柱柱高相同时，随腹板高度增加，构件承载力有所提升。腹板高度变化对中长柱的极限承载力影响较大，腹板高度增加，构件截面抗弯刚度有明显提升、侧向弯曲大幅降低。

4 破坏模式

将双肢梯形冷弯薄钢格构柱20种工况数值模型变参数分析得到的极限承载力Pmax和破坏模式汇总如图13所示，其中L表示局部屈曲；D表示畸变屈曲；FR表示绕实轴整体屈曲；FI表示绕虚轴整体屈曲。

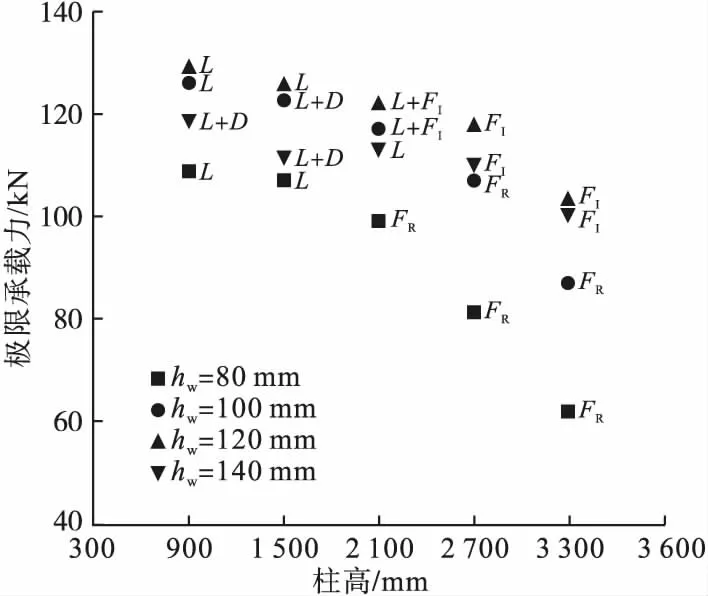
图13 破坏模式Fig.13Failure mode

通过有限元分析可知，双肢梯形冷弯薄钢格构柱的柱高及截面腹板高度对构件的承载性能和破坏模式影响显著。随着柱高增加，构件承载力呈下降趋势，且下降速率由缓及快，构件破坏模式由局压强度破坏转为整体失稳破坏。当柱高L≤2 100 mm时，主要为局压强度破坏和局部+畸变屈曲耦合破坏两种；当柱高L>2 100 mm时，主要发生整体失稳破坏，且随着腹板高度逐渐增加，破坏模式由绕实轴失稳转为绕虚轴失稳。

分肢截面腹板高度增加，格构柱轴压承载力有所提升，最大承载能力构件截面高hw在120 mm左右，且破坏模式以分肢跨中腹板处局部屈曲破坏为主导，同时伴有斜卷边畸变屈曲耦合破坏。因此,建议对双肢梯形冷弯薄钢格构柱的腹板高度取100～120 mm较为合适。

5 极限承载力

基于有限元分析软件ABAQUS计算结果，结合我国《冷弯薄壁型钢结构技术规范》(GB50018—2002)，采用有效宽度法对笔者所研究的双肢梯形冷弯薄钢格构柱进行轴压承载力计算，并将规范计算结果与有限元分析结果进行对比分析。规范中轴心受压构件的稳定承载力计算公式为

Nu=φAef.

(1)

式中:φ为轴心受压稳定系数；Ae为有效截面面积；f为钢材抗压强度设计值。同时以换算长细比λ0y来考虑构件绕虚轴失稳时剪切变形的影响：

(2)

式中:λy为整个构件对虚轴(y轴)的长细比；A为所有单肢毛截面面积之和；A1为构件横截面所截各斜缀条毛截面面积之和。式(1)中有效截面面积Ae由有效宽度be决定，具体计算步骤如下:

当b/t≤18αρ时：

be/t=bc/t.

(3)

当18αρ

(4)

当b/t≥38αρ时：

(5)

式中:b为板件宽度；t为板件厚度；be为板件有效宽度；α和ρ为计算系数；bc为板件受压区宽度。其计算结果如表1所示。

表1 薄钢规范计算结果与有限元分析结果对比Table 1Comparison between calculation results of thin steel specifications and finite element analysis results

由表1可知，当腹板高度hw≤120 mm时，规范有效宽度法计算值Nu与有限元模拟值PA吻合较好，结果偏于安全；而当腹板高度hw=140 mm时，有限元模拟结果与规范计算结果比值PA/Nu值依次为0.954、0.925、0.973、0.995、0.969，说明此时使用现行有效宽度法计算偏不安全。建议将式(1)中稳定系数φ进行修正，得出双肢梯形冷弯薄钢格构柱的承载力计算公式。

6 结 论

(1)双肢梯形冷弯薄钢格构柱随柱高增加轴压极限承载力降低速率先慢后快，当柱高L≤2 100 mm时构件总体发生局部屈曲时同时伴有畸变屈曲耦合；当柱高L>2 100 mm时破坏模式由强度破坏转为整体失稳破坏。

(2)改变截面腹板高度对格构柱的轴压性能影响也较显著。当腹板高度增大时，截面抗弯刚度明显增大，轴压承载力呈上升趋势，但当腹板高度增至一定值，因构件发生腹板局部屈曲失稳，轴压承载力反而降低。为保证较优承载性能，建议分肢截面腹板高度hw取100～120 mm。

(3)采用规范中有效宽度法对构件进行轴压承载力计算，腹板高度hw≤120 mm时理论计算结果总体偏于安全；腹板高度hw=140 mm时，理论计算值偏不安全，建议修正稳定系数φ，得出适用于双肢梯形冷弯薄钢格构柱的承载力计算公式。

(4)缀条式双肢梯形冷弯薄钢格构柱具有轴压承载性能高，整体受力均匀，破坏模式明确，截面形式灵活等优点。在强化弱轴惯性矩、提高构件双向抗弯性能的情况下降低了构件钢材使用量，可在轻型工业厂房或大跨度轻钢房屋中应用。