PVA-ECC-钢筋复合梁抗冲击的影响因素及破坏特性研究

齐宝欣,李宜人

(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168；2.大连理工大学海岸和近海工程国家重点实验室，辽宁 大连 116024)

随着土木工程领域中超级工程的大量施工建设，在对建筑结构的抗冲击、抗倒塌性能的要求越来越高。PVA增强纤维水泥基复合材料(PVA-ECC)由V.C.LI和C.K.Y.LEIMG[1]基于微观力学和断裂力学理论提出的新型纤维水泥基复合材料，具有强韧性[2-3]、抗疲劳性[4-5]和抗冲击性[6]的水泥基复合材料。因此，近些年来，PVA-ECC等水泥基复合材料得到了广泛的工程应用和推广[7-8]。

F.YUAN[9]采用ATENA有限元软件建立PVA-ECC钢筋复合梁的四点受弯三维实体模型，通过与试验结果对比验证了有限元模型的准确性。WANG Qiusheng[10]研究了钢纤维、玄武岩纤维和硫酸钙对高掺量粉煤灰聚乙烯醇(PVA)纤维基工程水泥基复合材料(ECC)力学性能的影响,分别进行了单轴拉伸、压缩和四点弯曲试验，对混合料的力学性能进行了表征。W.K.LEE等[11]研究了纤维增强混凝土与FRP筋配合使用，以减少梁的裂缝宽度，将改进的Gergely-Lutz模型应用于测量裂缝宽度，结果表明，FRP筋显著降低了纤维增强混凝土梁的最大裂缝宽度。H.WANG等[12]试验研究聚丙烯纤维增强混凝土梁的受弯性能，确定了纤维加固构件延性指标，改善了梁的弯曲性能。马益标[13]研究了PVA-ECC钢筋网加固后梁的抗弯、抗剪性能，结果表明，加固后提高了梁的抗弯、抗剪承载力、刚度和限制裂缝发展。王冲[14]研究PVA-ECC钢丝网加固混凝土板、梁的抗弯性能，加固后提高了结构的承载能力和刚度。赵培智[15]研究箍筋对钢筋增强ECC剪切试件的破坏模式，确定了钢筋种类、配箍率对增强钢筋ECC的抗剪性能的影响。目前，针对PVA-ECC-钢筋水泥基复合结构构件的力学性能研究主要以静力学为主，针对动荷载，尤其是冲击荷载作用下PVA-ECC-钢筋复合梁的动态破坏响应因素的研究成果较少。

基于此，笔者综合考虑单、多次冲击作用下PVA-ECC-钢筋复合梁抗冲击影响因素，通过数值模拟方法对比分析梁配筋参数、梁跨长度、冲击体质量和截面尺寸等因素对PVA-ECC-钢筋复合梁在多次冲击作用下抗冲击性能的影响。研究表明:随着冲击次数增加，PVA-ECC-钢筋复合梁跨中应力不断增大，且逐渐扩散至整个跨中部位；随着梁跨度的增加，PVA-ECC钢筋复合梁受冲击作用的影响越大。

1 有限元建模方法

1.1 有限元模型

笔者设计的PVA-ECC-钢筋复合梁，截面形式如图1所示。笔者采用ANSYS/LS-DYNA有限元软件，创建落锤、PVA-ECC梁、钢筋和约束刚体的实体模型。其中，落锤、混凝土梁和约束刚体均采用3D SOLID164单元，内部钢筋采用3D LINK 160单元见图2。其中，主要考虑钢筋配筋参数，截面尺寸、梁的跨度和落锤等模型参数，试件工况见表1。

图1 PVA-ECC-钢筋复合梁示意图Fig.1Schematic diagram of PVA-ECC-reinforced composite beam

图2 PVA-ECC-钢筋复合梁有限元模型Fig.2The finite element model of PVA-ECC- reinforced composite beam

1.2 材料本构模型参数

PVA-ECC采用脆性损伤本构模型，关键字为*MAT_BRITTLE_DAMAGE，PVA-ECC抗拉强度为9.17 MPa，抗压强度为78.6 MPa，拉伸初裂强度为4.0 MPa，弹性模量为2.0×104MPa，泊松比为0.2。落锤和支座约束采用刚体材料模型，关键字为*MAT_RIGID，密度为7.85×10-2g/mm3，弹性模量为2.0×105N/mm2，泊松比为0.3。钢筋采用各向同性硬化和随动硬化塑性模型，考虑应变率效应，关键字为*MAT_PASTIC_KINEMATIC，屈服强度为300 MPa，密度为7.85×10-2g/mm3，弹性模量为2.0×105MPa，泊松比为0.3，切线模量为2.0×103MPa，应变率效应参数C为5，P为40，失效应变为0.15。单元网格划分尺寸分别为PVA-ECC梁采用5 mm；落锤和支座约束单元划分为15 mm。梁与支座约束采用自动面面接触，接触摩擦系数为0.3。

1.3 模型验证

采用有限元软件ANSYS/LS-DYNA模拟PVA-ECC梁落锤冲击荷载作用下的破坏形态，数值模型建模依据文献[16-17]。模型的截面尺寸如图3所示。落锤冲击的位置在PVA-ECC梁跨中部位，有限元模型选取文献中的落锤高度1m，落锤质量7.34 kg的

表1 试件工况和模型参数Table 1Test conditions and model parameters

工况进行数值模拟和试验结果对比验证(见图4)。

图3 PVA-ECC梁示意图Fig.3Schematic diagram of PVA-ECC beam

图4 多次冲击下PVA-ECC梁的破坏模式Fig.4Failure mode of PVA-ECC beam under multiple impact

2 PVA-ECC-钢筋复合梁抗单次冲击的影响因素分析

2.1 梁纵向配筋

笔者研究PVA-ECC-钢筋复合梁的配筋参数对其在抗冲击性能方面的影响，数值模拟中分别设置了工况S1～S5，共5组PVA-ECC-钢筋复合梁，其冲击力时程曲线如图5所示。其中，PVA-ECC抗压、抗拉强度，梁跨度，冲击体质量和截面尺寸均相同，纵筋和箍筋配筋参数不同(见表1)。

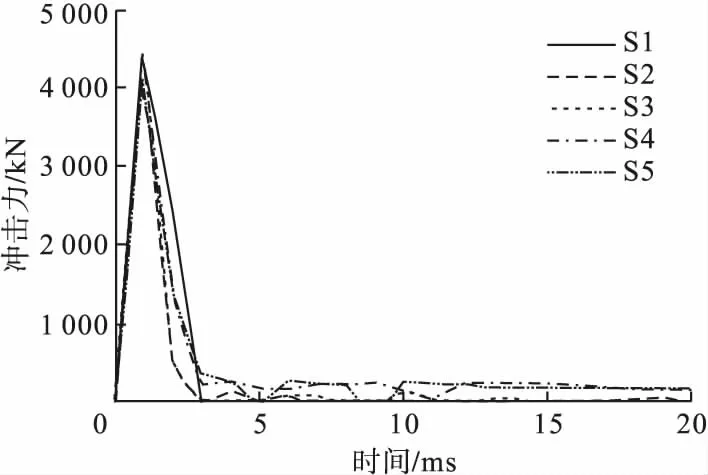
图5 S组梁冲击力时程曲线Fig.5The time history curve of impact force in S-groups beams

由图5可知，不同配筋率的PVA-ECC-钢筋复合梁的冲击力时程曲线。其中，到达冲击力峰值前，冲击力和时间成线性关系；当2.5 ms时，达到冲击力峰值后的S组(S1～S5)冲击力时程曲线略有不同(见图6)，原因是复合梁在受冲击后对首个冲击波的响应速度略缓，导致工况S1～S5各组复合梁冲击力时程曲线在短时间内出现无较大差别的现象。

图6 S组梁跨中位移时程曲线Fig.6The time history curve of mid-span displacement in S-groups beams

由图6可知，工况S1～S3复合梁所配钢筋仅箍筋直径不同，它们的跨中位移时程曲线相近，复合梁箍筋配筋率对梁的跨中最大位移影响较小。由S1、S4和S5复合梁的跨中位移时程曲线看出，随着纵筋配筋率增大，复合梁跨中位移减小；结果表明复合梁中纵筋配筋率越大，抗冲击性能越强。

2.2 梁跨度

笔者研究PVA-ECC-钢筋复合梁的跨度对其在抗冲击性能方面的影响，数值模拟中分别设置了工况L1～L4，共4组PVA-ECC-钢筋复合梁，其冲击力时程曲线如图7所示。其中，梁的配筋参数，PVA-ECC抗压、抗拉强度，冲击速度和截面尺寸均相同，跨度不同(见表1)。

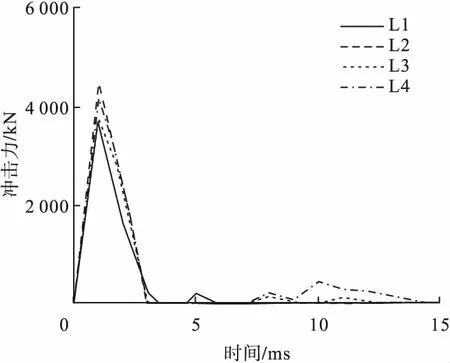
图7 L组梁冲击力时程曲线Fig.7The time history curve of impact force in L-groups beams

由图7可知，PVA-ECC-钢筋复合梁在冲击荷载作用之初冲击力和时间成线性关系，在受冲击后的前3 ms内,各复合梁的冲击力时程曲线趋势基本一致；随着复合梁跨度的增大，最大冲击力逐渐增加；考虑各复合梁在冲击作用之初主要受冲击体和PVA-ECC-钢筋复合梁之间的接触刚度作用，由于冲击体为自由落体，使得各复合梁在后续的受冲击过程中存在冲击体“反弹效应”，使得冲击力时程曲线有振荡发生。

跨度对冲击作用下PVA-ECC-钢筋复合梁的跨中位移有显著影响(见图8)。随着梁跨度的增加使得跨中位移的变化更大。工况L1和工况L4相比，振幅更小、自工况振更快；表明梁跨度越小，PVA-ECC-钢筋复合梁越能在受到冲击作用后出现更为迅速的自振响应，也就相当于梁跨越短抗冲击效果越好。

图8 L组梁跨中位移时程曲线Fig.8The time history curve of mid span displacement in L-groups beams

2.3 冲击速速

笔者研究PVA-ECC-钢筋复合梁在不同冲击速度作用时的破坏状态，数值模拟中分别设置了工况N1～N5，共5组PVA-ECC-钢筋复合梁，其冲击力时程曲线如图9所示。截面尺寸、配筋参数、PVA-ECC抗压抗拉强度和梁跨长度均相同，冲击速度不同(见表1)。为统一不同速度下的冲击体有相同冲击能量，通过改变冲击体自身质量来获得冲击体200 kg在1 m高处自由落体产生的冲击能量，以复合梁N3的冲击能量作为标准。

图9 N组梁冲击力时程曲线Fig.9The time history curve of impact forcein N-groups beams

由图9 可知，在工况N1(冲击体小球质量为15 kg、冲击速度为16.7 m/s)下，PVA-ECC-钢筋复合梁冲击力峰值远远高于其他工况；而冲击体速度越小，复合梁的冲击力峰值越小。

N组梁跨中位移时程曲线如图10所示。由图10可知，冲击速度低于8.85 m/s时，PVA-ECC-钢筋复合梁的跨中最大位移和残余位移都明显随着冲击速度的增加而变大，且速度越大，两者增加得越明显；当冲击速度高于11.43 m/s时，PVA-ECC-钢筋复合梁的跨中最大位移和残余位移随着冲击速度的增加而变大，且冲击体质量越大，梁跨中最大位移越大。因此，当冲击体质量较大时更应注意冲击速度，避免冲击荷载作用后的PVA-ECC-钢筋复合梁发生更大变形。

图10 N组梁跨中位移时程曲线Fig.10The time history curve of mid-span displacement in N-groups beams

N组梁冲击破坏模式如图11所示。

图11 N组梁冲击破坏模式Fig.11Impact failure modes of beams in N-groups

由图11可知，在PVA-ECC-钢筋复合梁冲击能量相同时，冲击体的质量越大、冲击速度越小，梁跨中受损区域越小，且跨中位置出现贯通的裂缝；冲击体质量越小、冲击速度越大，PVA-ECC-钢筋复合梁的跨中部位出现的耗能区域越大，有更多的PVA纤维参与进耗能过程。因此，PVA-ECC-钢筋复合梁越能够有效抵抗冲击荷载。

2.4 截面尺寸

笔者研究不同截面尺寸的PVA-ECC-钢筋复合梁在承受冲击作用时的破坏状态，数值模拟中分别设置了J组3个PVA-ECC-钢筋复合梁，其冲击力时程曲线如图12所示。截面长×宽分别为100 mm×250 mm、120 mm×250 mm、150 mm×250 mm，小球冲击速度、配筋参数、PVA-ECC抗压抗拉强度和梁跨长度均相同。

图12 J组梁冲击力时程曲线Fig.12The time history curve of impact force in J-groups beams

由图12可知，PVA-ECC-钢筋复合梁的截面尺寸在冲击荷载的初期对PVA-ECC-钢筋复合梁的影响不大，各PVA-ECC-钢筋复合梁所承受的最大冲击力虽然稍有不同，但在受冲击后的前3 ms内各PVA-ECC-钢筋复合梁的冲击力时程曲线基本一致，考虑各PVA-ECC-钢筋复合梁冲击作用之初主要受冲击体小球和PVA-ECC-钢筋复合梁之间的接触刚度作用，各PVA-ECC-钢筋复合梁仅在后续的受冲击过程中有较大的曲线走势改变。

J组梁跨中位移时程曲线如图13所示。由图13可知，截面尺寸对PVA-ECC-钢筋复合梁冲击作用后的跨中位移变化略有影响，跨中位移值随着截面形状短边长度的增加而减少，且短边长度越长，模型梁的振动频率越快，PVA-ECC-钢筋复合梁越能快速恢复平稳状态。

图13 J组梁跨中位移时程曲线Fig.13The time history curve of mid span displacement in J-groups beams

3 PVA-ECC-钢筋复合梁抗多次冲击影响因素分析

3.1 纵向配筋

由PVA-ECC-钢筋复合梁抗单次冲击影响因素的研究结果可知，箍筋配筋率对PVA-ECC-钢筋复合梁的抗冲击性能影响不大，而纵筋对其影响较为明显。因此，笔者主要研究配筋参数中纵筋对PVA-ECC-钢筋复合梁多次冲击荷载作用的影响。梁截面尺寸、PVA-ECC抗压强度、抗拉强度、梁跨长度和冲击体质量均相同，具体纵筋配筋参数见表1。C-S组梁跨中位移时程曲线如图14所示。

图14 C-S组梁跨中位移时程曲线Fig.14The time history curve of mid span displacement in C-S groups beams

由图14可知，随着PVA-ECC-钢筋复合梁内部纵筋直径的增大，梁的跨中最大位移不断减小；在第二次冲击荷载作用后，工况C-S1、C-S4和C-S5的跨中位移时程曲线差别较大，但曲线走势几乎相同，且工况C-S1、C-S4和C-S5在二次冲击后依然能保持振荡，说明依然有良好的抗冲击能力；PVA-ECC-钢筋复合梁内部纵筋直径越大，梁的自振频率越快；对比第二次与第一次冲击作用后梁的位移时程曲线，发现二次冲击作用时造成的相对位移较第一次冲击作用时的更大且第二次冲击后梁的自振振幅比第一次冲击作用时的大。

3.2 梁跨度

笔者研究PVA-ECC-钢筋复合梁多次冲击作用下的影响因素，其中，截面尺寸、配筋参数、PVA-ECC抗压强度、抗拉强度和冲击体质量均相同，复合梁跨度不同(见表1)。C-L组梁跨中位移时程曲线如图15所示。

图15 C-L组梁跨中位移时程曲线Fig.15The time history curve of midspan displacement in C-L groups beams

由图15可知，在PVA-ECC钢筋复合梁受到第二次冲击作用后，工况C-L2、C-L3和C-L4的位移时程曲线虽曲线趋势大致相同，但位移却有不同。随着梁跨度的增大，梁跨中最大位移越大；对比第二次与第一次冲击作用后梁的位移时程曲线，发现二次冲击作用时造成的相对位移较第一次冲击作用时的更大，但在二次冲击作用后依然能具备良好的抗冲击能力；同时工况C-S组具有第二次冲击后梁的自振振幅较第一次更大的特点。

3.3 冲击体质量

笔者针对冲击体质量分别为30 kg、50 kg 和100 kg时，PVA-ECC-钢筋复合梁多次冲击作用下的模拟分析，截面尺寸、配筋参数、PVA-ECC抗压强度、抗拉强度和梁跨长度均相同，具体参数见表1。C-N组各梁跨中位移时程曲线如图16所示。

图16 C-N组各梁跨中位移时程曲线Fig.16The time history curve of mid span displacement in C-N groups beams

由图16可知，PVA-ECC-钢筋复合梁的工况N4在第二次冲击作用后失效发生断裂破坏，PVA-ECC-钢筋复合梁的工况N2和工况N3在第二次冲击作用后依然能够有良好的抗冲击能力，梁的跨中最大位移随着冲击体质量的增加而变大，与C-S组和C-L组同样具有第二次冲击后梁的自振振幅较第一次更大且相对位移也更大的特点。

4 结 论

(1)PVA-ECC-钢筋复合梁冲击作用下，配筋因素导致的影响在最开始时不明显，在后续的冲击过程中影响明显，且梁中纵筋配筋率越高，梁跨中部位移就越小，说明纵筋配筋参数变化对PVA-ECC-钢筋复合梁受冲击后的挠度变化有很大影响，梁中箍筋配筋率对PVA-ECC-钢筋复合梁受冲击作用时的影响很小。

(2)梁跨长度的不同对PVA-ECC钢筋复合梁受冲击作用后的起初仅有较小的影响，当梁跨度为1.9 m时，受冲击作用后的中后期有显著的振荡作用效果，且梁跨中部位移最大。

(3)在冲击能量相同情况下，冲击体速度越大，PVA-ECC-钢筋复合梁的局部受破坏越明显，梁跨中部位出现的耗能区域越大，就有更多的PVA纤维参与耗能过程。

(4)随着冲击次数的增加，PVA-ECC-钢筋复合梁跨中应力不断增大；随冲击次数增加而逐渐扩散至整个跨中部位，由于PVA纤维的耗能能力和桥接作用，PVA-ECC-钢筋复合梁在受冲击后可通过发展多条细密小裂缝来耗散能量，可抵抗多次冲击，从而提升结构构件的安全性。