基于状态空间法的无柱型类矩形隧道分析模型

王金昌,范卫洲,黄伟明

(浙江大学建筑工程学院,浙江 杭州 310058)

盾构隧道是城市交通基础设施建设中重要的结构型式，伴随城市化进程的加速而成为地下工程建设的主流。在开挖浅埋隧道时，圆形盾构隧道因优良的结构受力性能成为隧道发展的主流，但此种形状的截面有效利用率较低；矩形隧道虽在断面利用率上占较大优势，但其发展受限于结构受力变形及施工工艺。因此，结构形式介于矩形与圆形间的异形隧道亟待研究与开发。其中，类矩形是由多段圆弧组合而成，类似于矩形断面的封闭断面。相比双线单圆隧道，单洞双线类矩形断面隧道在横向范围内可节省6 m左右的空间；相比单洞双圆隧道，单洞双线类矩形面隧道在竖向范围内空间节省量在4 m左右，且可不设中立柱，减振降噪也相对较为明显，在空间布置和使用上具有更大的灵活性[1]。相比于矩形隧道，可以避免四角的应力集中，具有更大的承载力。因此，探索类矩形结构受力的适应性，研究类矩形盾构的关键技术并逐步积累施工经验，能对城市的地下建设发展提供巨大的技术支持。

大断面异形衬砌结构设计的难点在于确定最优的盾构横截面尺寸与断面形式。在设计环节，获取隧道衬砌管片的内力与变形情况是隧道结构合理性分析的首要任务。现场监测法虽然直观，但其信息回馈速率不及模型试验[2]。在试验领域，朱瑶宏[3]、柳献[4]、张维熙[5]等针对类矩形隧道设计了足尺试验以获取管片结构特性。在数值模拟领域，有限元法是隧道结构模拟的重要工具，汤继新[6]、陈金铭[7]、邓声君[8]等利用ABAQUS有限元软件建立了类矩形盾构隧道的三维有限元模型，模拟分析了类矩形盾构施工引起的地层变形。有限元虽能够精细分析结构在复杂荷载、复杂接触下的力学行为，但也由此降低了分析效率，限制了其在设计阶段的应用。因此，简化力学分析模型较有限元法更适用于设计环节。黄伟明等[9]基于欧拉曲梁理论，采用状态空间法[10]，得到了弹性地基上连续曲梁的首末端状态变量传递关系，并用梁弹簧模型[11-12]模拟接头力学行为，最终得到了圆形盾构隧道的解析解。此种解析解的方法形式简洁，因便于编程，计算效率非常高，并且能够模拟任意荷载与接头分布形式下的管片力学行为。

笔者在黄伟明等对圆形盾构隧道解析研究的基础上，将各段管片的半径参数差异化，推导出由多段圆弧组成的无柱型类矩形隧道精确解析方法。通过ABAQUS有限元法对具体实例进行建模分析，对比解析解结果与有限元计算结果，验证解析解的准确性，并对土弹簧进行相应参数分析。最后应用解析法对几种具有相同断面利用率的类矩形隧道进行对比分析，研究类隧道的形状特征对其管片的受力与位移的影响，为类矩形盾构隧道尺寸设计优化与推广提供依据。

1 基本假定

类矩形隧道衬砌在横向是由管片以及管片间的接头组成的整体环形结构(见图1)。

图1 衬砌结构分析模型Fig.1Model scheme of a segmental lining

主要假定如下：①管片为线弹性材料；②不同半径管片于衔接处相切；③衬砌变形为小变形，管片力学行为符合欧拉曲梁理论，即满足平截面假定；④采用轴向、径向与转动方向的集中弹簧模拟接头的力学行为；⑤采用径向与切向的Winkler弹簧模拟衬砌和地层的相互作用。

2 类矩形隧道衬砌环解析模型

2.1 弹性地基上的曲梁模型

弹性地基上单个连续曲梁段(段内半径不变)受力如图2 所示。其中，衬砌中曲线半径为R，管片厚度为h，A与I分别为截面的面积和抗弯惯性矩，φ为截面转角。由于存在半径不同的管片段，对于圆心角θ的定义，以拱底为角度起点，段内绕圆心顺时针转动为正，如此曲梁分段的圆心角为[θ0，θ1]。因假定不同半径段于衔接处相切，因此绕类矩形隧道转动一圈仍为360°。坐标轴s轴沿衬砌中曲线建立，坐标轴z轴沿半径辐射方向建立，qs与qz为沿两个坐标系方向作用在衬砌上的分布荷载。径向位移记w，环向位移记为u，弯矩记为M，剪力记为Q，轴力记为N，正方向如图2所示。Winkler弹簧的径向抗力系数和环向抗力系数分别记作kz和ks。

图2 弹性地基上单个连续曲梁段模型Fig.2Model diagram of a curved beam resting on elastic foundation

黄伟明等推导了弹性地基上曲梁的状态方程，参数无量纲化后，方程改写为

(1)

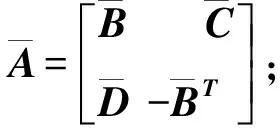
(2)

以单段管片为例，式(2)共有12个未知数，方程数为6，因此至少需要补充6个边界条件进行求解。

2.2 接头模型

采用轴向、径向与弯曲三个方向的线性弹簧来模拟接头。接头两侧力与位移关系为

(3)

无量纲化后，接头处的关系为

(4)

不同于黄伟明等推导的接头矩阵，由于不同半径管片段在无量纲化时不一致，因此在无量纲化后的接头传递矩阵中，需要对径向位移、轴向位移及弯矩相关项进行修正：

Jj=Rj/Rj+1001/k jw000Rj/Rj+1001/kju0001001/kjφ00010000001000000Rj/Rj+1éëêêêêêêêùûúúúúúúú.

(5)

为了将相同半径的管片段分离，方便编程及后续数值计算，需要人为地对管片进行分段，从而产生所谓的人工接头，此时接头的刚度可视为无穷大，即管片间连续(见图3)。

图3 衬砌环状态向量传递路线Fig.3Transmitting route of state vector

2.3 类矩形隧道衬砌环曲梁模型

按半径将管片衬砌分为n段，此时接头数量为n。从第一段管片起始端开始传递，结合单段管片内传递方程式(2)与管片间接头传递矩阵式(4)，即可得到第n段管片末端的状态向量：

(6)

而第一段管片的起始端与第n段管片的末端通过第n个接头相连，于是有

(7)

将式(7)代入至式(6)，可得整环传递的方程为

(8)

式(8)是关于6个状态向量的代数方程，进行求解后即可得到第一段管片起始端截面处的3个位移以及3个内力。继续利用式(2)与式(4)即可得到管片内任意截面处的内力及位移。

3 数值算例

3.1 模型验证

笔者以张子新等[13]针对上海地区第四层土(粉质黏土)设计的类矩形隧道为例，建立Abaqus有限元模型分析。然后将有限元结果与文中的解析解进行对比，分析过程中的模型参数保持一致。管片布置如图4所示，衬砌共由六块管片组成。

图4 类矩形隧道衬砌管片布置图Fig.4Sketch of the partition of the tunnel lining

由图可知，B1、B3、L1、L2管片分别由不同半径的管片段衔接而成，B2与F管片内半径保持一致。以B1管片为例，其由三段不同半径的管片段组成，各弧段分别以其圆心对角度θ计数，计数起点为最低点。以此角度计数，可得隧道接头的具体位置位于17.0°、96.5°、169.0°、197.0°、276.5°、349.0°。因计算分段需要，衔接处需要设立人工接头，位置分别为21.8°、60.7°、119.3°、158.2°、201.8°、240.7°、299.3°、338.2°。

衬砌外径由大到小分别为10.2 m、5.25 m与1.25 m，衬砌纵向环宽为1.2 m。土弹簧的径向抗力系数设为kz=6 000 kPa/m，环向抗力系数ks取径向抗力系数的1/3[14]。对于接头弹簧刚度，参考朱叶艇等[15]的研究，类矩形隧道衬砌接头转动刚度在正弯(内拉)状态下取1.2×105(kN·m)/rad，负弯(外拉)状态下取1×105(kN·m)/rad，计算时先暂时统一为正弯刚度；参考闫治国等[16]的接头试验，接头的径向刚度设为kw=2.4×105kN/m；一般接头的轴向刚度较大，因此设为ks=2×107kN/m。

根据图5中的加载与埋深情况，各项荷载分别设置为q1=210.4 kPa，q2=246.9 kPa，q3=168 kPa，q4=114 kPa，q5=12.5 kPa。ABAQUS有限元计算时，由于为平面问题，因此隧道管片采用二维梁单元模拟，管片间的接头采用两点间弹簧模拟，而土弹簧则采用接地弹簧模拟。

图5 衬砌荷载分布图Fig.5Distribution of ground pressure acting on lining

ABAQUS有限元计算结果与文中解析解结果对比如图6～图8所示。

图6 轴力计算结果对比Fig.6Comparison chart of axial forces

图7 弯矩计算结果对比Fig.7Comparison chart of bending moments

图8 径向位移计算结果对比Fig.8Comparison chart of radial displacements

由轴力、弯矩、径向位移对比结果可知，参数一致的情况下，文中解析解方法与ABAQUS有限元法计算结果非常接近。其中，轴力最大值位于管片B3，有限元结果与解析偏差为0.4%，轴力最小值位于管片F，有限元与解析偏差为-0.6%。左半环与右半环弯矩整体呈中心对称分布，正弯矩最大值位于管片F，有限元与解析偏差为0.4%，负弯矩最大值位于管片L1，有限元与解析偏差为0.4%。径向位移整体呈中心对称分布，正径向位移最大值位于B1管片与L1管片衔接处的接头位置，有限元与解析偏差为0.3%，负径向位移最大值位于拱顶，有限元与解析偏差为0.8%。以上结果均验证了文中解析解的正确性。

3.2 参数分析

考察土弹簧刚度系数对计算的影响，为便于分析，假定接头位置分布、管片截面几何特性、材料参数、衬砌半径以及荷载布置与上例一致。图9～图10分别给出了衬砌内力与径向位移最值，以及最值出现位置随土弹簧径向刚度系数kz的变化曲线。

图9 内力与径向位移最值随土弹簧刚度系数变化图Fig.9Variation of internal force and radial displacement with stiffness coefficient of soil spring

图10 内力与径向位移最值位置随土弹簧刚度系数变化图Fig.10Variation of maximum positions of internal force and radial displacement with stiffness coefficient of soil spring

由图9和图10可以得出：

(1)管片的最大最小轴力总体随土弹簧刚度系数的增大而减小，从幅度上来看，轴力最大值的变化受土弹簧刚度系数的影响更大一些。轴力最小值有一段不明显的增大段，推测在土弹簧刚度系数为103～104kPa/m内，由于拱顶正弯矩受到较大的抑制作用，限制了管片F接头的转动，而稍许增强了轴力的传递作用，因此拱顶轴力有所增大。而当土弹簧刚度系数继续增大时，土弹簧对内力的抑制趋势占主导，拱顶轴力随即迅速减小。

(2)管片的正负弯矩最值随土弹簧刚度系数的增大而减小，并逐渐趋向于零，曲线变化由平缓变得陡直，而后趋于平缓；变化幅度上，土弹簧刚度系数对正弯矩最值的抑制作用更大一些。

(3)管片径向位移最值随土弹簧刚度系数的增大而减小，并逐渐趋向于零，曲线变化由平缓变得陡直，而后趋于平缓。从变化幅度上看，土弹簧刚度系数对隧道拱顶与拱底位移的抑制作用更大一些。

(4)轴力最大值基本出现于B3管片，参考角度为300°～320°，当土弹簧刚度系数足够大时向内转移至B2管片；轴力最小值恒出现于F管片的拱顶附近。

(5)正弯矩最大值基本出现于拱顶附近，当土弹簧刚度系数足够大时，由于约束作用占主导，因此整体的弯矩波峰谷趋于缓和，最值位置转移至B1管片。负弯矩最大值相继出现于L2、L1与B3管片的小半径段，参考角度为240°±2°、127±7°、315±2°。

(6)隧道内缩最明显的位置相继出现于拱顶与拱底；外扩最明显的位置集中于左侧B1与L1管片的接头处，当土弹簧刚度系数足够大时，抑制作用占主导，隧道整体的径向位移趋于零，外扩位置零散分布于左右拱腰以上位置。

4 隧道形状对管片受力的分析

在解析解正确的基础上，进一步研究隧道形状对地层内管片内力和径向变形的影响。类矩形隧道沿着隧道边界的半径(R1、R2和R3)对应状况如图11所示。分别给出表面积近似相同的四组类矩形隧道形状与一组圆形隧道形状，各结构参数见表1。

图11 类矩形隧道半径布置图Fig.11Definition of the radius in quasi-rectangular tunnels

表1 各类矩形隧道结构参数表Table 1Geometrical parameters of tunnel shape cases

各组隧道在地下的空间利用率近乎一致时，宽高比反映隧道的扁平程度，其值越大，类矩形隧道整体越扁。对比分析时，仅改变隧道的形状特征(R1、R2与R3)，其余参数(弹簧刚度、结构接头布置、管片材料、管片厚度与隧道埋深等)与上例保持一致。由于半径的变化，衔接段人工接头的角度相应发生细微变化；由于隧道宽高改变，个别荷载也会相应改变，在参数分析时将考虑在内。各隧道内力与径向位移数值见表2，分别绘制各工况下的内力曲线与径向位移曲线，结果如图12～图14所示。

表2 各隧道内力与径向位移结果Table 2Results of structural forces and radial displacement induced in the tunnel lining

图12 各组隧道轴力对比图Fig.12Comparison of axial forces in each group

图13 各组隧道弯矩对比图Fig.13Comparison of bending moments in each group

图14 各组隧道径向位移对比图Fig.14Comparison of radial displacements in each group

从图12～图14和表2可以看出，与圆形隧道相比，类矩形隧道中产生的结构力与径向位移均更大。随着宽高比B/H的增加，拱顶与拱底处轴力有减小趋势，S4型类矩形隧道的最小轴力为1 009.01 kN，约为圆形隧道最小轴力的0.88倍。对应S1～S4工况，隧道大半径R1增加，拱顶与拱底的起拱逐渐缓和，因此减小了轴力的传递。而拱顶与拱底的弯矩呈增大趋势，S4类矩形隧道的最大正弯矩为434.36 kN·m，约为圆形隧道最大正弯矩的7.73倍。同时，相较于圆形隧道，类矩形隧道在小半径R2段会产生较大的负弯矩，S4类矩形隧道的最大负弯矩达到-482.03 kN·m。研究发现，负弯状态下的接头刚度会有所削弱，接头刚度本身也随接头工作状态呈非线性变化，因此若将接头的变化考虑其中，无柱型类矩形隧道的结构受力将更不利。

随宽高比B/H的增加，拱顶、拱底与拱腰的位移均相应增加，S4型类矩形隧道于拱顶附近的负径向位移达到约-11.10 mm，拱腰处的正径向位移达到约5.92 mm，隧道整体变形有竖缩和横扩趋势。在盾构法隧道结构服役性能鉴定与隧道结构安全控制中，横断面相对收敛均是重要的控制指标。对应径向收敛值最大的S4型类矩形隧道，在此种加载模式下，隧道拱顶与拱底轴线的相对收敛达到了22 mm，参考相应隧道保护标准，通常会将此种结构状况判定为Ⅱ类，即结构损伤较为严重。若直接投入地下使用，将会带来较大的安全隐患。

5 结 论

(1)土弹簧对隧道变形起抑制作用，随弹簧刚度增大，管片衬砌的内力与变形均逐渐减小。对于文中案例的类矩形隧道，荷载模式一致情况下，弹簧刚度在一定范围内，内力与位移最值出现的位置较为集中。

(2)通过隧道形状对管片行为的分析得到，在空间利用率相近的情况下，类矩形隧道的宽高比越大，管片衬砌产生的轴力整体有减小趋势，而弯矩与径向位移整体有增大趋势，管片外观的收敛变形更为明显。

(3)无柱型类矩形隧道因其特殊形状带来的结构受力上的劣势不可忽视，将其投入地下空间使用存在较大风险。未来可考虑通过增强管片自身的强度、提高接头刚度、设中立柱等方式提高可行性。