冲压过程对卷边蜂窝梁腹板受弯屈曲承载力的影响

许 峰,刘 翔,许 伟,王春刚

(沈阳建筑大学土木工程学院，辽宁 沈阳 110168)

蜂窝梁是腹板上带有规则孔洞的H形钢梁，其中一种制作方式是直接在腹板上开孔，其优点是可以任意调整开孔的大小、形状、位置等几何参数[1]。开孔后，其受力状态相较传统实腹梁更加复杂，孔间腹板屈曲成为蜂窝梁的主要破坏形式之一[2-4]。现有可避免此类破坏的措施有孔周设置加强套管或补强板[5]、孔间腹板设置横向加劲肋[6-7]或孔洞处设置对角线加劲肋[8]等。H.W.Al-Thabhawee等[9]对采用圆形和八边形套管补强的八边形孔蜂窝梁进行跨中集中力下的抗弯性能试验，结果表明，采用套管补强的蜂窝梁的极限承载力有较大提高且有良好的经济性。贾连光等[10]采用试验和有限元分析方法，对有无横向加劲肋的两种蜂窝梁在往复荷载作用下的破坏模式、局部稳定和滞回性能进行对比研究，结果表明，合理的加劲肋布置位置可有效地提高蜂窝梁的滞回性能。

近年来，国内外学者对于提高蜂窝梁稳定性措施的研究主要集中在加劲肋或套管方面。但加劲肋和套管的厚度较大，大量设置会显著增大梁的自重，浪费钢材，且现场施焊无法保证焊接质量。因此笔者提出了采用板材冲压翻边工艺，预制较小孔径的圆孔再冲孔的新型卷边蜂窝梁，在不显著增加蜂窝梁自重的前提下，孔周的卷边可以起到与加劲肋类似的作用。而冲压过程导致的残余应力对蜂窝梁腹板稳定性的影响尚未有学者进行研究。基于此，笔者以冲压过程的模拟为基础，探究残余应力对不同高厚比、开孔率、卷边半径和竖边长度下腹板稳定性的影响。研究表明：增加腹板厚度、竖边高度和卷边半径或减小开孔率可提高卷边蜂窝梁腹板的受弯屈性能。

1 回弹及减薄现象的模拟分析

普通翻边工艺过程原理如图1所示。将带有预制较小孔径的圆孔坯料放置在压边圈与凹模之间，在冲头的作用下预制孔周围的坯料被压入凹模，其孔径随着冲头下行而不断增大，直至被翻成竖边。经过多个孔洞的冲压后，最终形成的卷边蜂窝梁如图2所示。

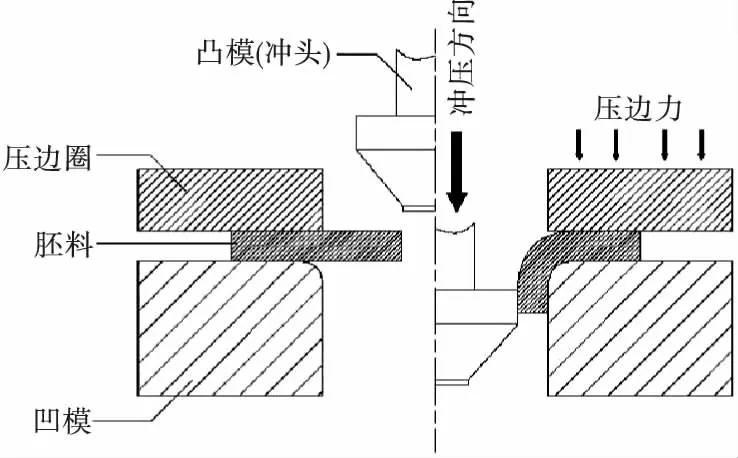
图1 翻边工艺过程示意图Fig.1Schematic of flanging process

图2 卷边蜂窝梁示意图Fig.2Schematic of castellated beam with curled web openings

由于构件在成型过程中会不可避免地产生弹性变形，冲压过程完成后，发生形变的部位必然会产生一定量的弹性变形的恢复，致使冲压件的形状与从模具中离开时的形状产生偏离，即产生回弹现象[11]，该过程的示意图如图3所示。近年来国内外学者对冲压成型工艺进行了大量研究和改进，极大地提高了对回弹的预测和控制的精度[12-14]。尽管板料上任一特定点的回弹量是很小的，但在发生弯曲的部位回弹会产生累计并在竖边下沿被放大。

图3 冲压过程中的角度变化、侧壁弯曲示意图Fig.3Schematic of angle variation and sidewall bending in flanging process

在合理的加工参数下，翻边后的竖边可以近似看作为仅受环向拉应力的单向受拉的应力状态，且应力大小随着深度的增加而增加，因此板料的壁厚也会随深度的增加而减薄[15]，翻边后竖边在下沿位置的厚度最小[16]。而实际情况中，翻边系数较小的情况下竖边中部还可能受到径向拉应力作用，产生局部壁厚过度减薄的现象。综上，冲孔过程中产生的回弹现象和变形区域减薄现象对卷边蜂窝梁的影响是必须要考虑的问题。

1.1 建立模型

采用通用有限元分析软件ABAQUS对板料的冲压回弹过程进行模拟，板料采用本构为理想弹塑性模型的Q355钢材，屈服强度为355 MPa。考虑各参数按照不同百分比波动时的灵敏度分析结果表明，弹性模量对回弹量的影响最大，因此忽略了对回弹量影响较小的硬化系数、硬化指数、初始屈服应力以及各向异性参数r0、r45和r90，弹性模量取210 GPa，泊松比取0.3。板料模型采用S4R单元，在变形较小的区域划分为10 mm的网格，在变形较大的圆孔边缘划分为5 mm的网格。凸、凹模和压边圈均设为离散刚体，采用R3D4单元，在与发生大变形的板料部分接触的区域划分为12 mm的网格；在凹模圆角处划分为3 mm大小的网格，以防止下模出现尖角而使板料发生过度扭转。

为探究不同高厚比、开孔率、卷边半径和竖边高度下蜂窝梁卷边处的回弹和减薄现象，将试验分为高厚比-开孔率、竖边高度-卷边半径两组各9个模型，每个模型的尺寸参数如表1、表2所示，模型尺寸参数如图4所示。

表1 第1组模型尺寸参数表Table 1Detailed dimensions of first group

表2 第2组模型尺寸参数表Table 2Detailed dimensions of second group

图4 尺寸参数示意图Fig.4Schematic of detailed dimensions

以h7r10为例的模型示意图如图5所示。

图5 h7r10模型示意图Fig.5Schematic of model h7r10

各尺寸参数下板料的预制孔径按式(1)分别计算[17]。其中，r为卷边半径，d为成型后孔径，t0为板料初始厚度，t′为冲压后板料平均厚度，h为竖边高度。

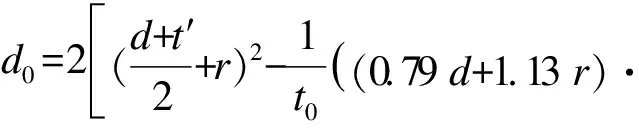
(1)

在分析步模块时，采用显示动力学进行预压和加载两个分析步，以保证发生大变形时模型收敛。在初始分析步中，在板料与凹模、压边圈的接触属性中，将网格较为粗糙的凹模和压边圈作为主面，网格较细的板料作为从面，摩擦系数取0.2，法向接触设为“硬”接触，并将所有设置传递至后续分析步。在预压分析步中，为有效减小弯曲部分的回弹现象[18]，对压边圈施加了较大的竖直向下的5 kN集中力，分析步时间设为0.05 s。在加载分析步中，板料与凸模的接触属性中，将网格较粗的凸模作为主面，网格较细的板料作为从面，摩擦系数取0.05，分析步时间设为0.1 s，使凸模下行直至冲压完成。由于卸载过程可以看作静态过程，因此卸载阶段采用静力通用分析步，将加载分析步的最后结果导入至新的静力分析步中作为板料的初始条件，删除冲头与板料的接触，其余部件的接触属性均由之前分析步传递，使板料自由回弹。

1.2 模拟结果验证

在模拟金属塑性成形过程时，由于模型运动速度一般不会很快，所以该过程属于静态分析的范畴。以h7r10模型为例，板料的动能(KE)和内能(IE)随冲头下行距离的变化曲线如图6所示。由图可知，动能远小于内能的5%，因此可以将此模型看作为准静态分析。

图6 动能、内能-冲头下行距离曲线Fig.6KE & IE-distance of punch load curve

为验证有限元模拟方法的正确性，将缺陷的关键参数的模拟结果与试验结果及理论公式进行对比。h7r10模型板料成型后的厚度分布云图如图7所示，其他参数的模型厚度分布与之类似，只有数值上略有差别。

图7 h7r10模型壁厚分布云图Fig.7Cloud chart of thickness distribution of model h7r10

翻边后竖边下沿可看作单向受拉的状态，其壁厚值按式(2)计算[16]：

(2)

式中：t0为板料的初始厚度;K为翻边系数。

第1组部分模型的实际减薄率和按式(2)计算的理论减薄率和减薄率差值如表4所示。由表可知，模拟试验的结果与理论分析结果的差值均不超过1%，因此可以认为模拟结果与理论分析结果吻合良好。

表4 实际与理论减薄率和减薄率差值Table 4Practical and theoretical ratio and difference of thickness reduction %

对比卜小芬[19]的试验数据，在相近的翻边系数(0.82)下，1.06 mm的板料减薄至0.93 mm，减薄率为12.26%，与模拟试验中t4d180模型的减薄率为9.50%的结果也十分接近，因此可以认为模拟结果与试验结果吻合良好。综上，模拟结果与试验结果与理论分析结果均吻合良好，验证了模型的正确性。

1.3 试验现象及回弹分析

以t3d150模型为例，在冲压过程中，冲头接触板料并下行时板料的S11应力分布云图如图8(a)所示，板料的弯曲部分处于径向受压的状态，同时竖边处于环向受拉的状态。随着冲头的继续下行，板料的弯曲部分开始出现环向受压的现象，而竖边则开始出现径向受拉的现象。冲压过程结束时板料的S11应力分布云图如图8(b)所示，板料的弯曲部分的下半部处于径向、环向双向受压的状态，上半部出现径向受拉的现象，竖边则处于双向受拉的状态。在回弹过程中，失去了冲头的约束，板料开始自由回弹，回弹结束时板料的S11应力分布云图如图8(c)所示，弯曲部分出现径向拉应力，使孔径减小，同时使竖边处于环向受压的状态。其他参数的模型的应力分布规律与上述相似，但随着竖边高度和板厚的增加，回弹后竖边的受压程度越来越严重；随着卷边半径的增加，回弹后弯曲部分的受拉程度越来越严重。

图8 t3d150模型S11应力分布云图Fig.8Cloud chart of S11 distribution of model t3d150

两组板料回弹前后孔径的变化率如表5所示。由表5可以得出，在上述4个参数的影响下，板料的孔径变化率没有明显的规律且均在0.4%以下，因此板料的回弹对孔径的影响是可以忽略的。

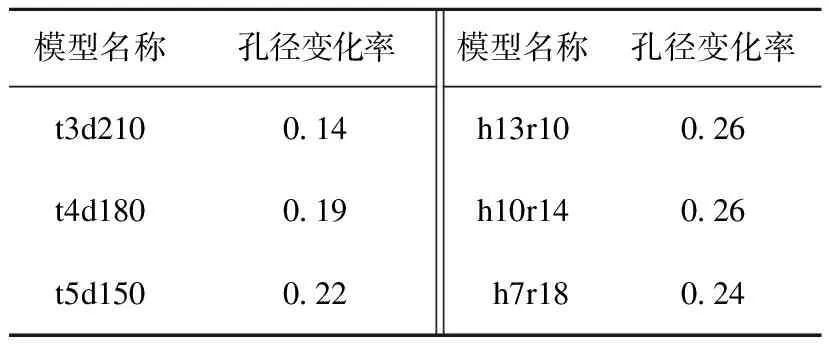
表5 孔径变化率Table 5Change rate of aperture %

2 冲压导致的残余应力对卷边蜂窝梁受弯屈曲承载力的影响

在实腹梁的腹板稳定分析中，传统的方法是单独考虑板的稳定，笔者采用类似的方法进行腹板的稳定性分析。圆孔蜂窝梁的腹板是一系列有规则的开孔腹板，因此可以看成是多个开一个圆孔腹板相连而成。由于动力学分析过程需耗费大量时间，因此笔者仅模拟单个开孔腹板的冲压过程并做后续分析。冲压得到的卷边起到加劲肋的作用，防止腹板发生局部失稳，因此可以通过比较分析残余应力的和完善的两种卷边蜂窝梁腹板的受弯屈曲荷载大小来判断冲压导致的缺陷对卷边蜂窝梁的影响。

2.1 残余应力对不同高厚比和开孔率的卷边蜂窝梁腹板的影响

在传统蜂窝梁中，腹板的高厚比和开孔率是影响其受弯屈曲承载力的两个重要参数，因此在卷边蜂窝梁中有必要研究这两个参数对受弯屈曲承载力的影响以及其对冲压导致的残余应力的敏感度。采用与前述相同的单元类型、网格尺寸、材料模型和求解方法先建立有缺陷的卷边蜂窝梁腹板模型，腹板的厚度t分别为4 mm、4.5 mm和5 mm，成型后孔径d分别为150 mm、165 mm、180 mm、195 mm、210 mm和225 mm。腹板的高度均为300 mm，孔间腹板宽度均为100 mm，卷边半径和竖边高度均为10 mm,模型的命名规则与1.1节中相同，冲压前腹板的预制孔径仍根据(1)式分别计算。

冲压和回弹的模拟分析步骤与前述完全相同，将回弹后保留残余应力和位移分布的结果导入buckle分析步中进行屈曲分析。在屈曲分析中，约束腹板上下边缘的平面外位移，并在下边缘两个角点处限制刚体位移；在腹板左右两侧施加等大反向的单位弯矩，经过屈曲分析后部分尺寸腹板的屈曲模态如图9所示。再建立与冲压完成后的卷边蜂窝梁腹板尺寸完全相同的、完善的腹板模型进行屈曲分析，经过屈曲分析后部分尺寸腹板的屈曲模态如图10所示。

图9 冲压后腹板的屈曲模态Fig.9Buckling mode of stamped web

图10 完善腹板的屈曲模态Fig.10Buckling mode of flawless web

由图9、图10可知，有缺陷的和完善的两种腹板的屈曲模态几乎完全相同，均为左右边缘上半部分由于受压而发生反对称的局部屈曲。由于两种腹板的屈曲模态几乎相同，因此仅以t=2.5 mm、d=150 mm的完善腹板为例将屈曲前后的模型进行对比，其正反两个方向的模态如图11所示。

图11 屈曲前后的模态对比Fig.11Comparison of modes between before and after buckling

腹板的左侧边缘上半部分A向Z轴正向发生鼓曲，使该处临近的卷边B处于受压的状态；右侧上半部分C向Z轴负向发生鼓曲，使该处临近的卷边D处于受拉的状态。冲压后和完善腹板的受弯屈曲承载力对比如图12所示。相较于完善的腹板，经过冲压的板料的卷边中弯曲部分分布着径向受拉残余应力，而竖边内分布着环向受压残余应力，当B处受压时其受拉残余应力可抵消部分压应力，当D处受拉时其受压残余应力可抵消部分拉应力，因此冲压后腹板的受弯屈曲承载力略高于完善的腹板，但提高的幅度绝大部分在10%以下。

图12 不同厚度的腹板屈曲荷载随孔径的变化Fig.12Variation of buckling load with aperture when web with different thickness

从图中还可得到与传统蜂窝梁类似的结论[20]：随着板厚的增加，卷边蜂窝梁腹板的屈曲荷载大幅增加。但传统蜂窝梁的屈曲荷载会随着开孔率的增加而迅速降低，而卷边蜂窝梁的屈曲荷载随开孔率的增大仅有小幅度的降低，且随着板厚的降低，屈曲荷载随开孔率增大而降低的幅度越来越小，说明卷边对较薄的腹板有更强的支撑作用。

2.2 残余应力对不同卷边半径和竖边高度的卷边蜂窝梁腹板的影响

由2.1节可知，卷边弯曲部分和竖边的残余应力对弯曲屈曲承载力的提高有显著作用，因此应进一步分析卷边半径和竖边高度对卷边蜂窝梁受弯屈曲承载力的影响。仍采用与前述相同的方法和本构关系先建立冲压的卷边蜂窝梁腹板模型，腹板的厚度t均为4 mm，成型后孔径d均为180 mm，高度均为300 mm，孔间腹板宽度w均为100 mm，卷边半径分别为10 mm、12 mm、14 mm、16 mm、18 mm和20 mm，竖边高度分别为5.5 mm、7 mm、8.5 mm、10 mm、11.5 mm和13 mm，模型的命名规则与1.1节中相同。冲压前腹板的预制孔直径仍根据式(1)分别计算。

冲压、回弹和屈曲分析步骤均与前述完全相同。再建立与冲压完成后的卷边蜂窝梁腹板尺寸完全相同的、完善的腹板模型并进行屈曲分析，屈曲分析中的边界条件、约束等均与前述一致，完善的腹板的屈曲模态与冲压后的腹板的屈曲模态几乎完全相同，且均与2.1节中的类似。

冲压后和完善的腹板的屈曲承载力对比图如图13所示。由图13可知，冲压后腹板的受弯屈曲承载力高于完善的腹板，其原因与2.1节中所分析的相同，不再赘述。

图13 不同竖边高度的腹板屈曲荷载随卷边半径的变化Fig.13Variation of buckling load with edge radius of crimping when web with different vertical height

经过冲压的板料的卷边中弯曲部分分布着径向受拉残余应力，竖边内分布着环向受压残余应力，且随着卷边半径和竖边高度的增加，其上分别分布受拉残余应力和受压残余应力的面积也越来越大，相较于完善的腹板，其上所能分别抵消的压应力和拉应力更大，因此第2组模型中经过冲压的腹板的屈曲承载力的提高幅度相较第1组而言更大。从图中还可得出，随着卷边半径和竖边高度的增加，腹板的受弯屈曲承载力均有小幅度的提高。

在卷边总长度较大(卷边半径r≥18 mm且竖边高度h≥11.5 mm)的情况下，虽然腹板的屈曲承载力提高较大，但此时的翻边系数较小，导致对加工设备的要求较高，因此在实际应用中并不推荐使用。而在卷边总长度较小(卷边半径r≤18 mm且竖边高度h≤11.5 mm)的情况下，其屈曲承载力提高的幅度绝大部分在10%以下，因此可以偏保守地认为冲压过程造成的残余应力仅不致对卷边腹板屈曲承载力有削弱作用，可按完善的腹板开展后续的研究工作。

3 结 论

(1)在完整的冲压-回弹过程中，卷边上的弯曲部分的受力状态从最初的径向受压逐渐变为径向和环向的双向受压，最终回弹结束时变为径向受拉；竖边的受力状态从最初的环向受拉逐渐变为双向受拉，最终变为环向受压。由应力重分布导致的孔径变化均在0.4%以下，因此可以忽略回弹导致的孔径减小。

(2)随着板厚的增大，卷边腹板的受弯屈曲承载力显著增大；随着孔径的增大，由于卷边的存在，其受弯屈曲承载力仅有小幅度的降低；随着卷边半径和竖边高度的增大，其受弯屈曲承载力均有小幅度的提高。

(3)在合理的加工参数下，考虑了回弹、减薄和残余应力的卷边腹板与完善的卷边腹板相比，其受弯屈曲承载力仅有小幅度的提高，因此可认为冲压过程对卷边腹板仅无负面作用，而由于有限元方法在冲压过程模拟中的计算成本过大，因此可按完善的卷边腹板开展后续的研究工作。